三角形的三边关系[下学期]
文档属性
| 名称 | 三角形的三边关系[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 575.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-04 00:00:00 | ||
图片预览






文档简介
课件24张PPT。自己动手试一试有这样的四根小棒
40cm、10cm、30cm、25cm ,
请你任意取其中的三根,
首尾连接,搭成三角形。从四根中任意取出三根有以下四种取法:
(1)40cm、10cm、30cm
(2)40cm、25cm、30cm
(3)25cm、10cm、30cm
(4)40cm、10cm、25cm能不能能不能§7.1 三角形的三边不等关系A—B
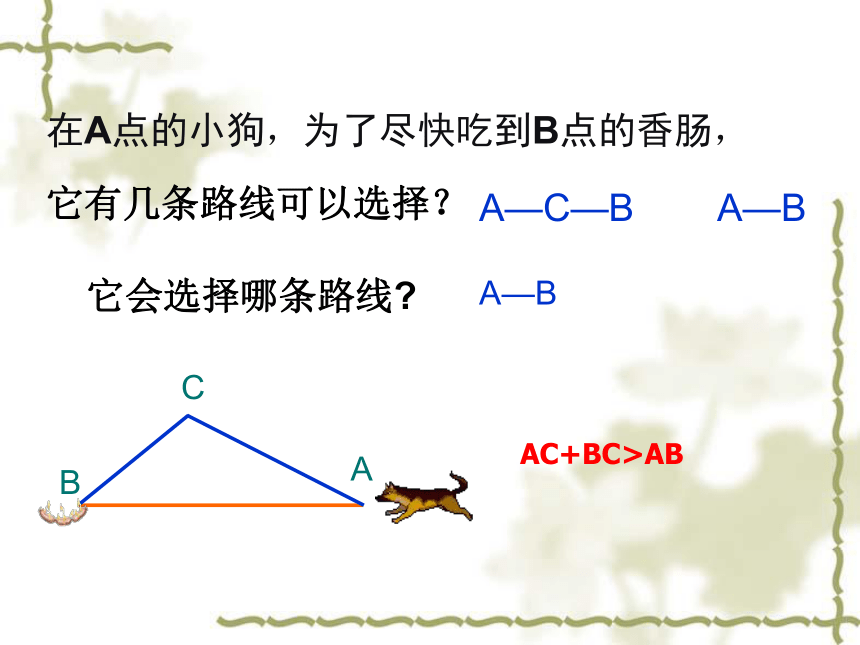
在A点的小狗,为了尽快吃到B点的香肠,
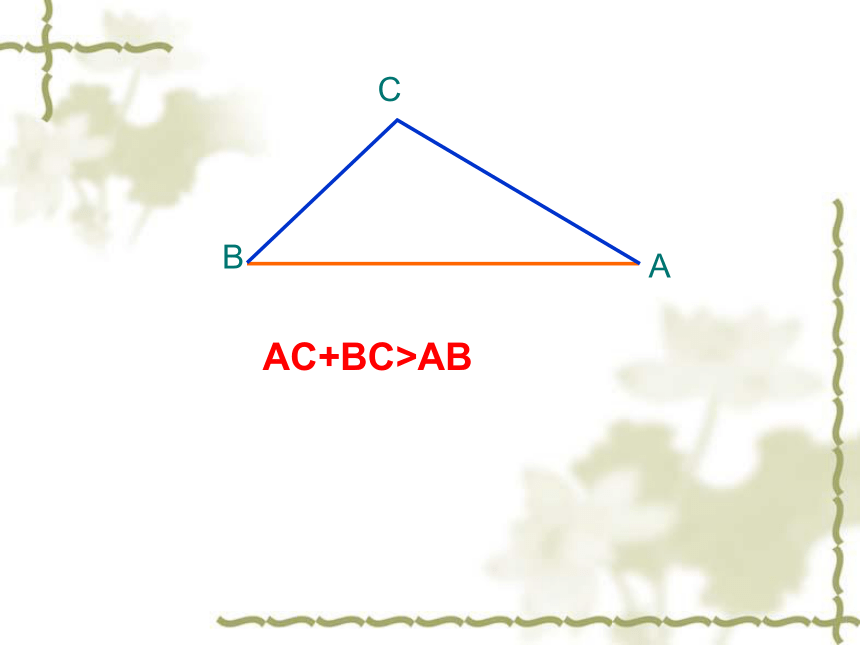
它有几条路线可以选择?BCAAC+BC>AB
它会选择哪条路线?A—C—B A—B BACAC+BC>AB(2) 6, 8 , 4 ( ) .下列长度的三条线段能否组成三角形?为什么?(1) 1 , 2, 5 ( )不能例解:因为6+8>4, 6+4>8,8+4>6,
所以这三条线段能组成一个三角形.解:因为1+2<5,
所以这三条线段不能组成一个三角形.能(3) 10 , 5,6 ( )(4) 2, 11 , 9 ( )能不能解:因为10+5>6, 6+5>10,10+6>5,
所以这三条线段能组成一个三角形.解:因为9+2=11,
所以这三条线段不能组成一个三角形.只要满足较小的两条线段之和大于第三条线段,
便可构成三角形;若不满足,则不能构成三角形.(5) 4, 6, 9解:因为4+6>9, 6+9>4,4+9>6,
所以这三条线段能组成一个三角形.( 能 )只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形. 1。下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、7cm、4cm (4) 4cm、5cm、6cm (2) 因为4cm+5cm<10cm,
所以这三条线段不能组成一个三角形. (3) 因为3cm+4cm=7cm,
所以这三条线段不能组成一个三角形. (4) 因为4cm+5cm>6cm,
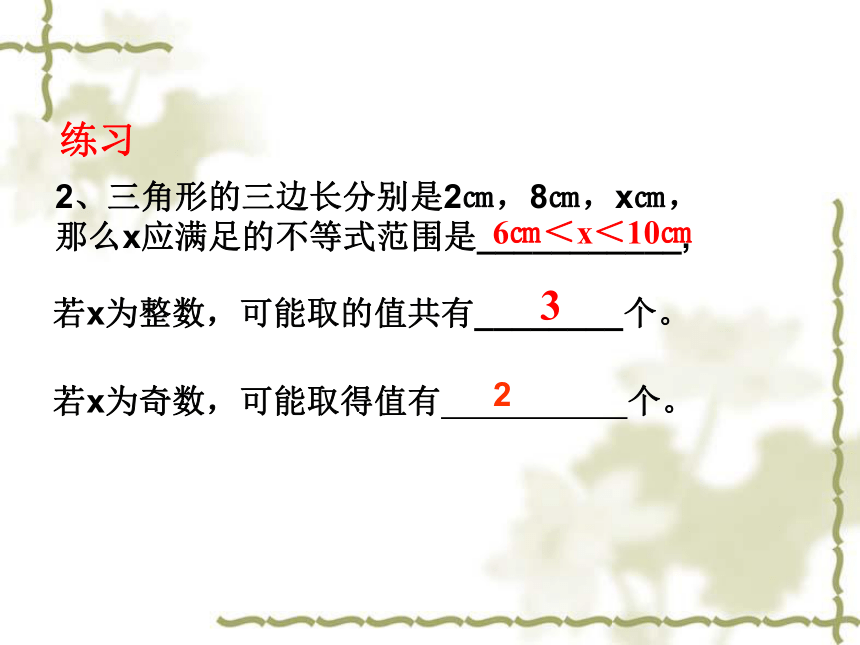
所以这三条线段能组成一个三角形.练一练①三角形的任意两边之和大于第三边②三角形任意两边之差小于第三边。③两边之差<第三边<两边之和. 三角形的三边不等关系: 若x为整数,可能取的值共有________个。2、三角形的三边长分别是2㎝,8㎝,x㎝,
那么x应满足的不等式范围是___________,6㎝<x<10㎝3若x为奇数,可能取得值有 个。 2练习试一试3.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?小颖有5种选法。第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm2、已知两条边长分别为2cm、5cm,
你可以画出几个符合条件的等腰三角形?做一做:1、已知两条边长分别为3cm、5cm,你可以
画出几个符合条件的等腰三角形?并求符合
条件的等腰三角形的周长. (3) 以长为3cm、5cm、7cm、10cm的四条线段中的
三条线段为边,可构成_____个三角形.比一比(1)任何三条线段都能组成一个三角形 ( ) (2)因为a+b>c,所以a、b、c三边可以构成三角形( )(4)已知等腰三角形的两边长分别为8cm,3cm,
则这三角形的周长为 ( ) (A) 14cm (B)19cm
(C) 14cm或19cm (D) 不确定 ××2B大
道草坪想一想:尽管草地不允许踩,但弄不好还是被踩出了一条小路,这是为什么?草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。拓展与应用!ADCBHH′到A、C距离之和最近的点在哪儿?到B、D呢?小结:通过这一节课的学习,你有什么收获? 1、三角形三边满足什么样的关系?2、如何判断三条线段能否构成三角形?3、数学知识在我们生活中有很多应用,
以后要认真地学好数学。再见
智力大冲浪用3根长度相等的火柴棒可以搭成一个等边三角形(如图1),用5根长度相等的火柴棒可以搭成一个等腰三角形(如图2),用12根长度相等的火柴棒可以搭成几个三角形?它们分别是什么三角形?等腰三角形等边三角形直角三角形我学会了 3、三角形的稳定性1、三角形的三边关系定理;(2)确定三角形第三边的取值范围:
两边之差<第三边,
两边之和>第三边.课后作业:1、作业本2、能力超越题(我要试试,加油!)(1)已知三角形三边长为整数2,x-3,4,则共
可作出不同形状的三角形?当x为多少时,所
作三角形周长最长?(2) 已知三条线段a,b,c,满足下列关系式:
c=2a,b+2a =3c.这三条线段的长能组
成三角形吗?若能,请说明理由;若不能,请
举一个例子说明.
(3) 用16根等长的火柴棒摆成的三角形中,最长边
最多可以由____根火柴棒组成由三条不在同一条直线上的线段首尾顺次连结组成的平面图形,称为三角形.你能说出三角形有哪些性质吗?不在同一条直线上首尾顺次连结(4) 3,5,8 ( )(3) 5,6,10 ( )(2) 2,5,6 ( ) .下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )不能能能不能例只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.1、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,问第三条线段a应
取的范围是多少? 试一试: 2、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,且第三条线段a的
长为奇数,问第三条线段应取多少长? 2cmAC
AC+BC>AB
AB+AC>BC
BC>AB-AC AC>BC- AB AB>AC- BC
40cm、10cm、30cm、25cm ,
请你任意取其中的三根,
首尾连接,搭成三角形。从四根中任意取出三根有以下四种取法:
(1)40cm、10cm、30cm
(2)40cm、25cm、30cm
(3)25cm、10cm、30cm
(4)40cm、10cm、25cm能不能能不能§7.1 三角形的三边不等关系A—B
在A点的小狗,为了尽快吃到B点的香肠,
它有几条路线可以选择?BCAAC+BC>AB
它会选择哪条路线?A—C—B A—B BACAC+BC>AB(2) 6, 8 , 4 ( ) .下列长度的三条线段能否组成三角形?为什么?(1) 1 , 2, 5 ( )不能例解:因为6+8>4, 6+4>8,8+4>6,
所以这三条线段能组成一个三角形.解:因为1+2<5,
所以这三条线段不能组成一个三角形.能(3) 10 , 5,6 ( )(4) 2, 11 , 9 ( )能不能解:因为10+5>6, 6+5>10,10+6>5,
所以这三条线段能组成一个三角形.解:因为9+2=11,
所以这三条线段不能组成一个三角形.只要满足较小的两条线段之和大于第三条线段,
便可构成三角形;若不满足,则不能构成三角形.(5) 4, 6, 9解:因为4+6>9, 6+9>4,4+9>6,
所以这三条线段能组成一个三角形.( 能 )只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形. 1。下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、7cm、4cm (4) 4cm、5cm、6cm (2) 因为4cm+5cm<10cm,
所以这三条线段不能组成一个三角形. (3) 因为3cm+4cm=7cm,
所以这三条线段不能组成一个三角形. (4) 因为4cm+5cm>6cm,
所以这三条线段能组成一个三角形.练一练①三角形的任意两边之和大于第三边②三角形任意两边之差小于第三边。③两边之差<第三边<两边之和. 三角形的三边不等关系: 若x为整数,可能取的值共有________个。2、三角形的三边长分别是2㎝,8㎝,x㎝,
那么x应满足的不等式范围是___________,6㎝<x<10㎝3若x为奇数,可能取得值有 个。 2练习试一试3.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?小颖有5种选法。第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm2、已知两条边长分别为2cm、5cm,
你可以画出几个符合条件的等腰三角形?做一做:1、已知两条边长分别为3cm、5cm,你可以
画出几个符合条件的等腰三角形?并求符合
条件的等腰三角形的周长. (3) 以长为3cm、5cm、7cm、10cm的四条线段中的
三条线段为边,可构成_____个三角形.比一比(1)任何三条线段都能组成一个三角形 ( ) (2)因为a+b>c,所以a、b、c三边可以构成三角形( )(4)已知等腰三角形的两边长分别为8cm,3cm,
则这三角形的周长为 ( ) (A) 14cm (B)19cm
(C) 14cm或19cm (D) 不确定 ××2B大
道草坪想一想:尽管草地不允许踩,但弄不好还是被踩出了一条小路,这是为什么?草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。拓展与应用!ADCBHH′到A、C距离之和最近的点在哪儿?到B、D呢?小结:通过这一节课的学习,你有什么收获? 1、三角形三边满足什么样的关系?2、如何判断三条线段能否构成三角形?3、数学知识在我们生活中有很多应用,
以后要认真地学好数学。再见
智力大冲浪用3根长度相等的火柴棒可以搭成一个等边三角形(如图1),用5根长度相等的火柴棒可以搭成一个等腰三角形(如图2),用12根长度相等的火柴棒可以搭成几个三角形?它们分别是什么三角形?等腰三角形等边三角形直角三角形我学会了 3、三角形的稳定性1、三角形的三边关系定理;(2)确定三角形第三边的取值范围:
两边之差<第三边,
两边之和>第三边.课后作业:1、作业本2、能力超越题(我要试试,加油!)(1)已知三角形三边长为整数2,x-3,4,则共
可作出不同形状的三角形?当x为多少时,所
作三角形周长最长?(2) 已知三条线段a,b,c,满足下列关系式:
c=2a,b+2a =3c.这三条线段的长能组
成三角形吗?若能,请说明理由;若不能,请
举一个例子说明.
(3) 用16根等长的火柴棒摆成的三角形中,最长边
最多可以由____根火柴棒组成由三条不在同一条直线上的线段首尾顺次连结组成的平面图形,称为三角形.你能说出三角形有哪些性质吗?不在同一条直线上首尾顺次连结(4) 3,5,8 ( )(3) 5,6,10 ( )(2) 2,5,6 ( ) .下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )不能能能不能例只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.1、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,问第三条线段a应
取的范围是多少? 试一试: 2、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,且第三条线段a的
长为奇数,问第三条线段应取多少长? 2cm
AC+BC>AB
AB+AC>BC
BC>AB-AC AC>BC- AB AB>AC- BC
