比例的应用 例1 比例尺 (教案)人教版六年级下册数学
文档属性
| 名称 | 比例的应用 例1 比例尺 (教案)人教版六年级下册数学 |

|
|
| 格式 | doc | ||
| 文件大小 | 408.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-26 16:40:53 | ||
图片预览



文档简介
比例尺
教学内容
人教版六年级《数学》下册P51例1
教学目标
1.结合具体情境,使学生理解比例尺的意义以及分类,掌握求比例尺的方法,掌握数值比例尺与线段比例尺互相改写的方法。
2.使学生通过观察、猜测、推理、计算、绘图等活动,体验数学与生活的联系,培养学生综合应用所学知识解决问题的能力。
3.使学生在观察、思考和交流等活动中培养分析、抽象、概括的能力,进一步体会数学知识之间的联系,感受学习数学的乐趣,培养学生“学数学,用数学”的意识和创新精神。
学情分析
“比例尺”是运用数学解决生活问题的一个典型范例之一。本节课,要通过在生活中的应用,把握比例尺的内涵——图上距离与实际距离的比,认识两种不同的比例尺——数值比例尺和线段比例尺。学生已经有了比和比例有关知识的基础,对于常见的平面图和地图并不陌生,但对“比例尺”这个概念可能会有些生疏和抽象。六年级的学生已经具备了较强的自主学习和合作学习的能力,教材对比例尺的概念也介绍得比较清楚,学生通过自学很快明白什么是比例尺,所以本节课运用学生自学、教师梳理的方式展开教学。课堂上我将借助学生已有的知识和经验引导学生,主动建构知识,给学生提供充分动手操作、动脑思考的时间和空间,让学生真正经历“比例尺”知识的形成过程,切实落实以学生为主体的新课标理念。
教学重点
理解比例尺的意义、比例尺分类,会说出数值比例尺与线段比例尺的含义。
教学难点
能根据实际情况选择比例尺,解决生活中的一些实际问题。
教学准备
课件、刻度尺。
教学过程
一、揭示课题,引发思考
师:今天我们要一起来研究比例尺,关于比例尺你想知道什么?
预设板书:1.概念; 2.用途;3.与比例有什么关系? 4.比例尺是尺吗……
二、先学后教,完善理解
(一)自学课本,初步认识
师:好,根据刚刚你们提的这几个问题请你自学一下书本第51页的内容。
生自学课本。
(二)集体反馈,理解意义
师:看一下,哪些问题我们马上就可以解决了?
板书:图上距离与实际距离的比叫做比例尺。
师:书上还介绍了什么?补充板书:数值比例尺、线段比例尺,形式。
师:同学们对比例尺已经有初步的了解了,现在来检验一下你们的学习成果。
1.认识数值比例尺
(1)板书:1:100
师:这个比例尺表示什么意思呢?
预设:图上距离是实际距离的:实际距离是图上距离的100倍;图上画1厘米,代表了实际距离100厘米。
出示:有一幅图的比例尺是1:100,你觉得下列哪个距离画在图上是8厘米呢?
A.课桌的长 B.教室的长 C.操场的长 D.乍浦到平湖的距离
小结:他们都是根据图上距离8厘米和比例尺在想实际距离是多少。
(2)平湖市地图它的比例尺应该是几比几比较合适呢?我们一起来看。出示:能说说你对这个比例尺的理解吗?
师:这两个比例尺在图上的距离都是1cm,但表示的实际距离分别是100cm和50 0000cm,那你对这两个比例尺有什么感觉?
生静想、同桌讨论
小结:它们相同的地方都是把实际距离缩小了,一个只是把实际距离缩小得一点点,一个缩小得很多很多。
2.认识线段比例尺。沟通数值比例尺和线段比例尺的意义,顺势沟通比例尺和正比例的关系。
出示中国地图,投影比例尺:
现实生活中还有这样的比例尺,认识吗?这种比例尺的图上距离和实际距离在哪里?(学生上来量)。黑板上这一段就代表了1cm,(黑板上画线段,并标98千米)那图上距离2厘米就表示?3厘米表示?
师:能转化成上面这样的比例尺吗?
板书:1 cm:98km =1 cm:980 0000cm=1:980 0000
这里,任意两点之间的图上距离与实际距离的比都等于。(板书:=),也就是比例尺一定时,图上距离和实际距离成什么关系?
像这样用一条标有数据的线段来表示地面上相对应的实际距离,就叫线段比例尺,而这种直接用数值来表示图上距离和实际距离的比,就叫数值比例尺。
3.介绍求比例尺
师:刚才这两幅地图的比例尺已经告诉我们了,那如果我要知道一幅图的比例尺,需要知道什么呢?刚才我们看了例1,看懂了吗?
生说师板书例题。问:2.4cm是表示?120km是?第1步在做什么?然后呢?
明确求比例尺要先统一单位,再化简。(板书:求比例尺)
三、分层练习,深入理解
1.算一算,比一比
看来同学已经理解了比例尺的意义,那你能试着求出下面这两幅图的比例尺吗?
(1)从平湖市到杭州市的实际距离大约为120km,请动手测量(取整厘米数)并计算这幅图的比例尺。
(2)一种机械手表的精密零件长5mm,王叔叔把它画在图纸上,量得其长是4cm。这张图的比例尺是多少?
A.生尝试练习,投影作业;
第1题,明确先统一单位,再把比例尺化简成最简整数比。
第2题,投影1:8和8:1,问:怎么会这样呢?到底哪个对?为什么呢?(指向概念:图上距离:实际距离)
B.共同评价,得出结论。那你说比例尺1:8和8:1有什么不一样?
板书:
1 : 8 8 : 1
小结:现实生活中,有些东西画在图上画不下,就需要把实际距离按一定的比缩小,而一些精密零件本身很小,画在图纸上时就需要按一定的比放大,这就是比例尺的用途。
学生纠错。
师:其实,在我们以前学习的位置与方向中,也隐藏着我们今天学的知识,我们一起来看。
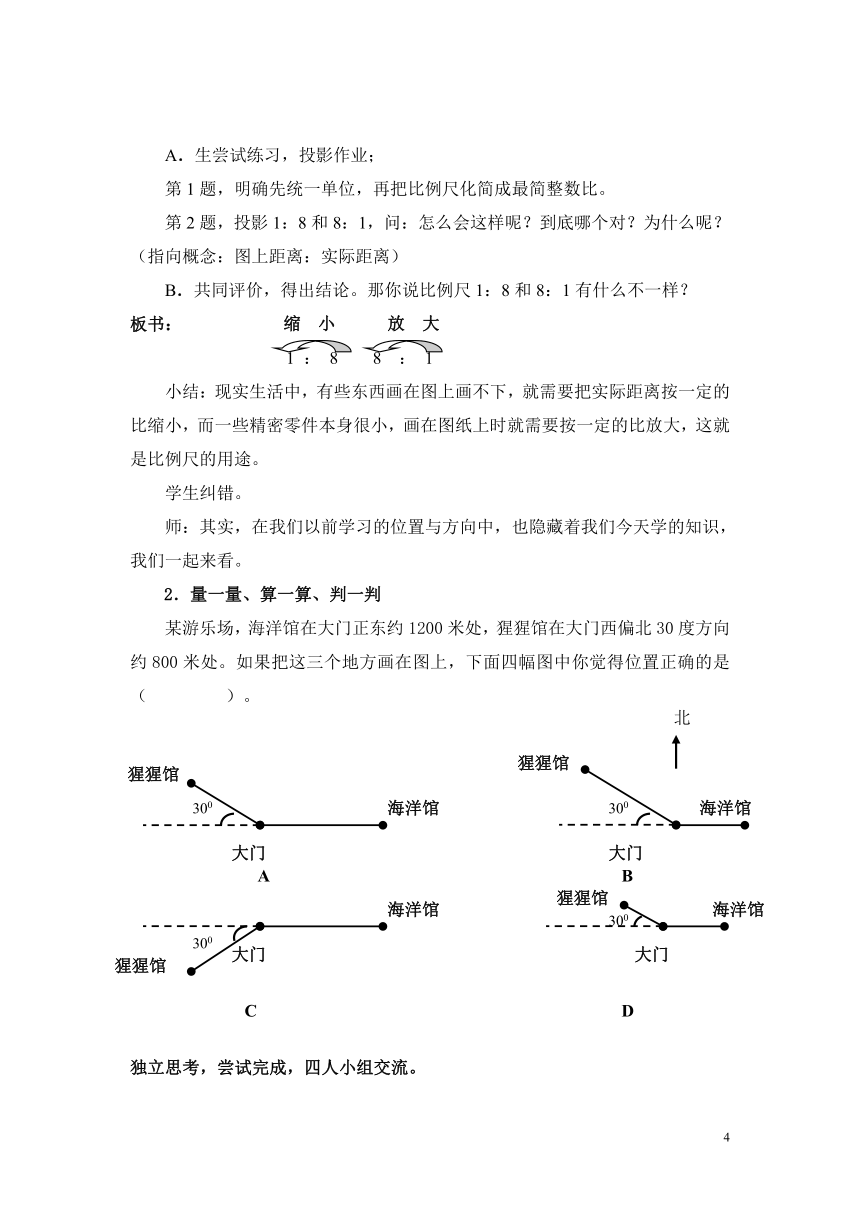
2.量一量、算一算、判一判
某游乐场,海洋馆在大门正东约1200米处,猩猩馆在大门西偏北30度方向约800米处。如果把这三个地方画在图上,下面四幅图中你觉得位置正确的是( )。
独立思考,尝试完成,四人小组交流。
反馈:
(1)先排除B和C。
C:上北下南,左西右东,这个是表示西偏南30度,方向不对,另外三个方向都对。
B:距离不对,大门到海洋馆的距离应该比大门到猩猩馆的距离要长。
(2)A和D是否正确我们需要怎么来判断呢?好,现在你可以量一量再算一算,看看A和D是否正确。
层次一:求比例尺
A图: 2cm:800m=2cm:80000 cm=1:40000
3cm:1200m=3cm:120000cm=1:40000
D图:1cm:800m=1cm:80000 cm=1:80000
1.5cm:1200m=1.5cm:120000 cm=1:80000
层次二: 1200m:800m=3:2, 3cm:2cm=3:2, 1.5cm:1cm=3:2,
小结:通过计算我们发现A和D都是可以的。那你知道造成这两幅图大小不一样的原因是什么了吗?
3.想一想,选一选
看来同学们都学得不错,现在请你们帮老师出出主意:老师想买一套大一点的房子,现在有两张商品房平面图纸供我挑选。你认为应该选( )。
A. B.
师:你们的意思是光看图不行?为什么?
出示:
A.比例尺1: 100 B.比例尺1:200
师:现在呢,你会选哪一个? 同桌讨论一下;说说你的想法。
预设:两图左边实际距离一样长,下面这条边图上距离相同,比例尺分别是1:100和1:200,所以下边图B是图A的2倍。
小结:看来我们只看图是不行的,还要知道这幅图的比例尺才能做出判断。
四、全课小结
师:这节课,我们学习了比例尺,现在你知道了比例尺的哪些知识?
教学反思
本节课把关注点聚焦到图上距离和实际距离的关系表示方法上,学生借助比较、讨论、交流等自主学习形式,探索发现比例尺的意义和表示方法。呈现地图和零件图纸中的比例尺,借助生活中真实情境,深化了对比例尺意义的理解。最后练习环节也借助房屋平面图、七星瓢虫等问题巩固本节课所学内容。本节课内容比较多,学生可能会有混淆,数值比例尺与线段比例尺的改写以及求放大比例尺时出错较多,教师要注意抓住细节指导。
作业设计
1.一幅图的比例尺是1∶50000,它表示图上距离是实际距离的(150000)。
2.是(线段)比例尺,它表示图上(1cm)的距离相当于实际距离(5)km,把它改写成数值比例尺是()。
3.把数值比例尺1∶80000改写成线段比例尺是
4.甲地到乙地的实际距离是5km,在一幅地图上是10cm,这幅地图的比例尺是多少?
答案:5km=500000cm
10cm∶500000cm=1∶50000
答:这幅地图的比例是1∶50000。
5.一个零件在图纸上画出来的高度是2cm,它的实际高度是4mm。这幅图纸的比例尺是多少?
答案:4mm=0.4cm
2∶0.4=5∶1
答:这幅图纸的比例尺是5∶1。
6.一种长8mm的精密零件,画在图纸上长4cm,这幅图纸的比例尺是多少?
答案:4cm∶8mm=40mm∶8mm=5∶1
答:这幅图纸的比例尺是5∶1。
附学习单
《比例尺》练习纸 姓名
算一算,比一比
量一量、算一算、判一判
某游乐场,海洋馆在大门正东约1200米处,猩猩馆在大门西偏北30度方向约800米处。如果把这三个地方画在图上,下面四幅中你觉得正确的是 ( ) 。
(正确的理由是什么?可以把你的想法用算式的形式写在练习纸上)
平湖市
缩 小
放 大
海洋馆
海洋馆
猩猩馆
C
D
300
大门
猩猩馆
海洋馆
大门
猩猩馆
大门
海洋馆
大门
猩猩馆
A
B
300
300
300
北
12厘米
6厘米
10厘米
10厘米
(2)一种手表的精密零件长5mm,把它画在图纸上,量得其长是4cm。这张图的比例尺是多少?(如下图2)
(1)从平湖市到杭州市的实际距离大约为120km,请动手测量(取整厘米数)并计算这幅图的比例尺。(如下图1)
平湖市
图2
图1
北
猩猩馆
猩猩馆
300
300
海洋馆
海洋馆
大门
大门
B
A
猩猩馆
海洋馆
海洋馆
300
300
大门
大门
猩猩馆
D
C
PAGE
1
教学内容
人教版六年级《数学》下册P51例1
教学目标
1.结合具体情境,使学生理解比例尺的意义以及分类,掌握求比例尺的方法,掌握数值比例尺与线段比例尺互相改写的方法。
2.使学生通过观察、猜测、推理、计算、绘图等活动,体验数学与生活的联系,培养学生综合应用所学知识解决问题的能力。
3.使学生在观察、思考和交流等活动中培养分析、抽象、概括的能力,进一步体会数学知识之间的联系,感受学习数学的乐趣,培养学生“学数学,用数学”的意识和创新精神。
学情分析
“比例尺”是运用数学解决生活问题的一个典型范例之一。本节课,要通过在生活中的应用,把握比例尺的内涵——图上距离与实际距离的比,认识两种不同的比例尺——数值比例尺和线段比例尺。学生已经有了比和比例有关知识的基础,对于常见的平面图和地图并不陌生,但对“比例尺”这个概念可能会有些生疏和抽象。六年级的学生已经具备了较强的自主学习和合作学习的能力,教材对比例尺的概念也介绍得比较清楚,学生通过自学很快明白什么是比例尺,所以本节课运用学生自学、教师梳理的方式展开教学。课堂上我将借助学生已有的知识和经验引导学生,主动建构知识,给学生提供充分动手操作、动脑思考的时间和空间,让学生真正经历“比例尺”知识的形成过程,切实落实以学生为主体的新课标理念。
教学重点
理解比例尺的意义、比例尺分类,会说出数值比例尺与线段比例尺的含义。
教学难点
能根据实际情况选择比例尺,解决生活中的一些实际问题。
教学准备
课件、刻度尺。
教学过程
一、揭示课题,引发思考
师:今天我们要一起来研究比例尺,关于比例尺你想知道什么?
预设板书:1.概念; 2.用途;3.与比例有什么关系? 4.比例尺是尺吗……
二、先学后教,完善理解
(一)自学课本,初步认识
师:好,根据刚刚你们提的这几个问题请你自学一下书本第51页的内容。
生自学课本。
(二)集体反馈,理解意义
师:看一下,哪些问题我们马上就可以解决了?
板书:图上距离与实际距离的比叫做比例尺。
师:书上还介绍了什么?补充板书:数值比例尺、线段比例尺,形式。
师:同学们对比例尺已经有初步的了解了,现在来检验一下你们的学习成果。
1.认识数值比例尺
(1)板书:1:100
师:这个比例尺表示什么意思呢?
预设:图上距离是实际距离的:实际距离是图上距离的100倍;图上画1厘米,代表了实际距离100厘米。
出示:有一幅图的比例尺是1:100,你觉得下列哪个距离画在图上是8厘米呢?
A.课桌的长 B.教室的长 C.操场的长 D.乍浦到平湖的距离
小结:他们都是根据图上距离8厘米和比例尺在想实际距离是多少。
(2)平湖市地图它的比例尺应该是几比几比较合适呢?我们一起来看。出示:能说说你对这个比例尺的理解吗?
师:这两个比例尺在图上的距离都是1cm,但表示的实际距离分别是100cm和50 0000cm,那你对这两个比例尺有什么感觉?
生静想、同桌讨论
小结:它们相同的地方都是把实际距离缩小了,一个只是把实际距离缩小得一点点,一个缩小得很多很多。
2.认识线段比例尺。沟通数值比例尺和线段比例尺的意义,顺势沟通比例尺和正比例的关系。
出示中国地图,投影比例尺:
现实生活中还有这样的比例尺,认识吗?这种比例尺的图上距离和实际距离在哪里?(学生上来量)。黑板上这一段就代表了1cm,(黑板上画线段,并标98千米)那图上距离2厘米就表示?3厘米表示?
师:能转化成上面这样的比例尺吗?
板书:1 cm:98km =1 cm:980 0000cm=1:980 0000
这里,任意两点之间的图上距离与实际距离的比都等于。(板书:=),也就是比例尺一定时,图上距离和实际距离成什么关系?
像这样用一条标有数据的线段来表示地面上相对应的实际距离,就叫线段比例尺,而这种直接用数值来表示图上距离和实际距离的比,就叫数值比例尺。
3.介绍求比例尺
师:刚才这两幅地图的比例尺已经告诉我们了,那如果我要知道一幅图的比例尺,需要知道什么呢?刚才我们看了例1,看懂了吗?
生说师板书例题。问:2.4cm是表示?120km是?第1步在做什么?然后呢?
明确求比例尺要先统一单位,再化简。(板书:求比例尺)
三、分层练习,深入理解
1.算一算,比一比
看来同学已经理解了比例尺的意义,那你能试着求出下面这两幅图的比例尺吗?
(1)从平湖市到杭州市的实际距离大约为120km,请动手测量(取整厘米数)并计算这幅图的比例尺。
(2)一种机械手表的精密零件长5mm,王叔叔把它画在图纸上,量得其长是4cm。这张图的比例尺是多少?
A.生尝试练习,投影作业;
第1题,明确先统一单位,再把比例尺化简成最简整数比。
第2题,投影1:8和8:1,问:怎么会这样呢?到底哪个对?为什么呢?(指向概念:图上距离:实际距离)
B.共同评价,得出结论。那你说比例尺1:8和8:1有什么不一样?
板书:
1 : 8 8 : 1
小结:现实生活中,有些东西画在图上画不下,就需要把实际距离按一定的比缩小,而一些精密零件本身很小,画在图纸上时就需要按一定的比放大,这就是比例尺的用途。
学生纠错。
师:其实,在我们以前学习的位置与方向中,也隐藏着我们今天学的知识,我们一起来看。
2.量一量、算一算、判一判
某游乐场,海洋馆在大门正东约1200米处,猩猩馆在大门西偏北30度方向约800米处。如果把这三个地方画在图上,下面四幅图中你觉得位置正确的是( )。
独立思考,尝试完成,四人小组交流。
反馈:
(1)先排除B和C。
C:上北下南,左西右东,这个是表示西偏南30度,方向不对,另外三个方向都对。
B:距离不对,大门到海洋馆的距离应该比大门到猩猩馆的距离要长。
(2)A和D是否正确我们需要怎么来判断呢?好,现在你可以量一量再算一算,看看A和D是否正确。
层次一:求比例尺
A图: 2cm:800m=2cm:80000 cm=1:40000
3cm:1200m=3cm:120000cm=1:40000
D图:1cm:800m=1cm:80000 cm=1:80000
1.5cm:1200m=1.5cm:120000 cm=1:80000
层次二: 1200m:800m=3:2, 3cm:2cm=3:2, 1.5cm:1cm=3:2,
小结:通过计算我们发现A和D都是可以的。那你知道造成这两幅图大小不一样的原因是什么了吗?
3.想一想,选一选
看来同学们都学得不错,现在请你们帮老师出出主意:老师想买一套大一点的房子,现在有两张商品房平面图纸供我挑选。你认为应该选( )。
A. B.
师:你们的意思是光看图不行?为什么?
出示:
A.比例尺1: 100 B.比例尺1:200
师:现在呢,你会选哪一个? 同桌讨论一下;说说你的想法。
预设:两图左边实际距离一样长,下面这条边图上距离相同,比例尺分别是1:100和1:200,所以下边图B是图A的2倍。
小结:看来我们只看图是不行的,还要知道这幅图的比例尺才能做出判断。
四、全课小结
师:这节课,我们学习了比例尺,现在你知道了比例尺的哪些知识?
教学反思
本节课把关注点聚焦到图上距离和实际距离的关系表示方法上,学生借助比较、讨论、交流等自主学习形式,探索发现比例尺的意义和表示方法。呈现地图和零件图纸中的比例尺,借助生活中真实情境,深化了对比例尺意义的理解。最后练习环节也借助房屋平面图、七星瓢虫等问题巩固本节课所学内容。本节课内容比较多,学生可能会有混淆,数值比例尺与线段比例尺的改写以及求放大比例尺时出错较多,教师要注意抓住细节指导。
作业设计
1.一幅图的比例尺是1∶50000,它表示图上距离是实际距离的(150000)。
2.是(线段)比例尺,它表示图上(1cm)的距离相当于实际距离(5)km,把它改写成数值比例尺是()。
3.把数值比例尺1∶80000改写成线段比例尺是
4.甲地到乙地的实际距离是5km,在一幅地图上是10cm,这幅地图的比例尺是多少?
答案:5km=500000cm
10cm∶500000cm=1∶50000
答:这幅地图的比例是1∶50000。
5.一个零件在图纸上画出来的高度是2cm,它的实际高度是4mm。这幅图纸的比例尺是多少?
答案:4mm=0.4cm
2∶0.4=5∶1
答:这幅图纸的比例尺是5∶1。
6.一种长8mm的精密零件,画在图纸上长4cm,这幅图纸的比例尺是多少?
答案:4cm∶8mm=40mm∶8mm=5∶1
答:这幅图纸的比例尺是5∶1。
附学习单
《比例尺》练习纸 姓名
算一算,比一比
量一量、算一算、判一判
某游乐场,海洋馆在大门正东约1200米处,猩猩馆在大门西偏北30度方向约800米处。如果把这三个地方画在图上,下面四幅中你觉得正确的是 ( ) 。
(正确的理由是什么?可以把你的想法用算式的形式写在练习纸上)
平湖市
缩 小
放 大
海洋馆
海洋馆
猩猩馆
C
D
300
大门
猩猩馆
海洋馆
大门
猩猩馆
大门
海洋馆
大门
猩猩馆
A
B
300
300
300
北
12厘米
6厘米
10厘米
10厘米
(2)一种手表的精密零件长5mm,把它画在图纸上,量得其长是4cm。这张图的比例尺是多少?(如下图2)
(1)从平湖市到杭州市的实际距离大约为120km,请动手测量(取整厘米数)并计算这幅图的比例尺。(如下图1)
平湖市
图2
图1
北
猩猩馆
猩猩馆
300
300
海洋馆
海洋馆
大门
大门
B
A
猩猩馆
海洋馆
海洋馆
300
300
大门
大门
猩猩馆
D
C
PAGE
1
