数学八年级上青岛版2.4线段的垂直平分线(1)课件
文档属性
| 名称 | 数学八年级上青岛版2.4线段的垂直平分线(1)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 391.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-10 00:00:00 | ||
图片预览



文档简介
课件16张PPT。
青岛版 《数学》八年级(上)2.4线段的垂直平分线
------(第1课时)1、能说出线段的垂直平分线的定理和逆定理,会区别运用这两个定理。
2、体会学习数学的方法,观察,概括,验证,比较等在本课时中的应用。
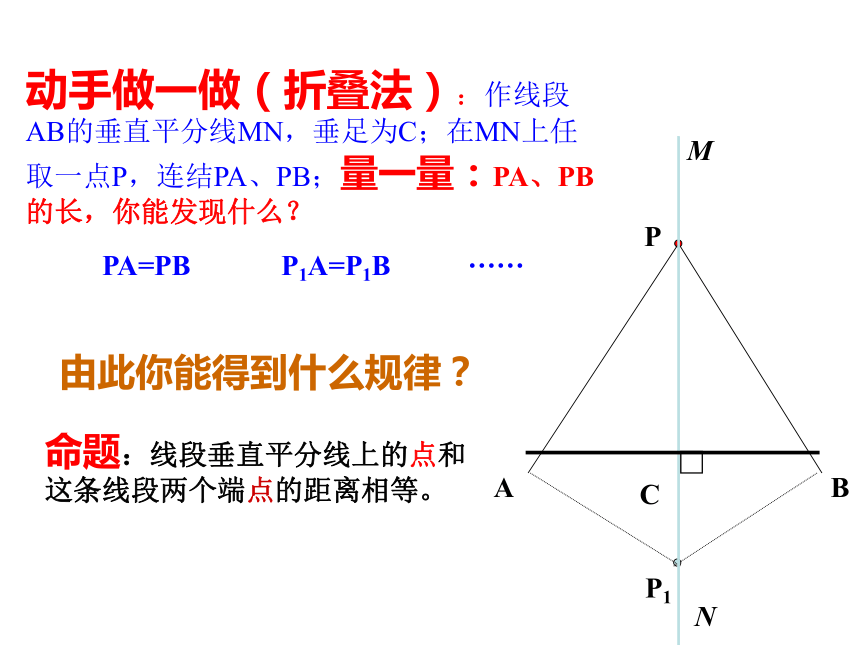
3、认识数学来源于生活,又服务于现实生活,体验数学的应用价值。教学目标PA=PBP1P1A=P1B……命题:线段垂直平分线上的点和这条线段两个端点的距离相等。由此你能得到什么规律?命题:线段垂直平分线上的点和这条线段两个端点的距离相等。C应用举例:
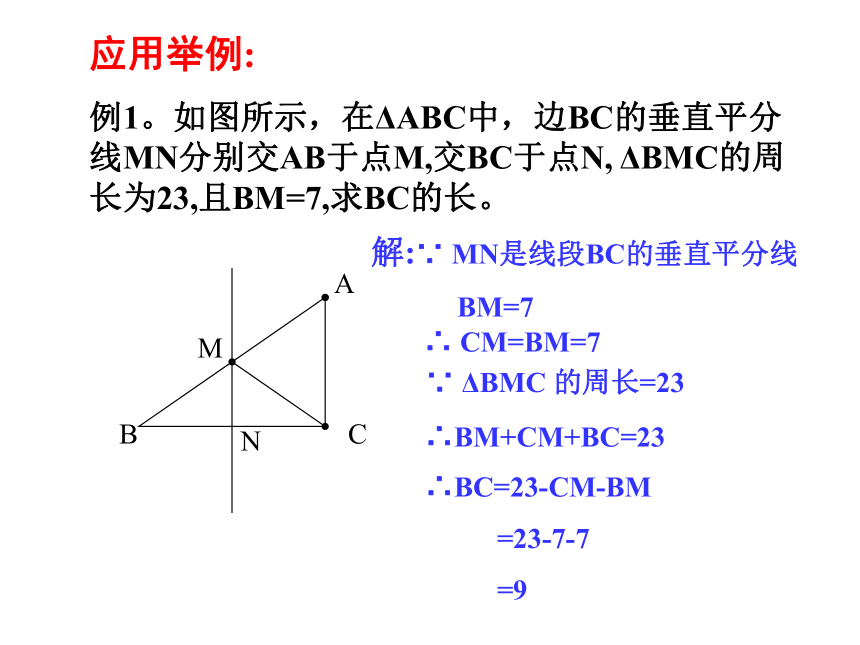
例1。如图所示,在ΔABC中,边BC的垂直平分线MN分别交AB于点M,交BC于点N, ΔBMC的周长为23,且BM=7,求BC的长。解:∵ MN是线段BC的垂直平分线
BM=7 ∴ CM=BM=7 ∵ ΔBMC 的周长=23∴BM+CM+BC=23∴BC=23-CM-BM
=23-7-7
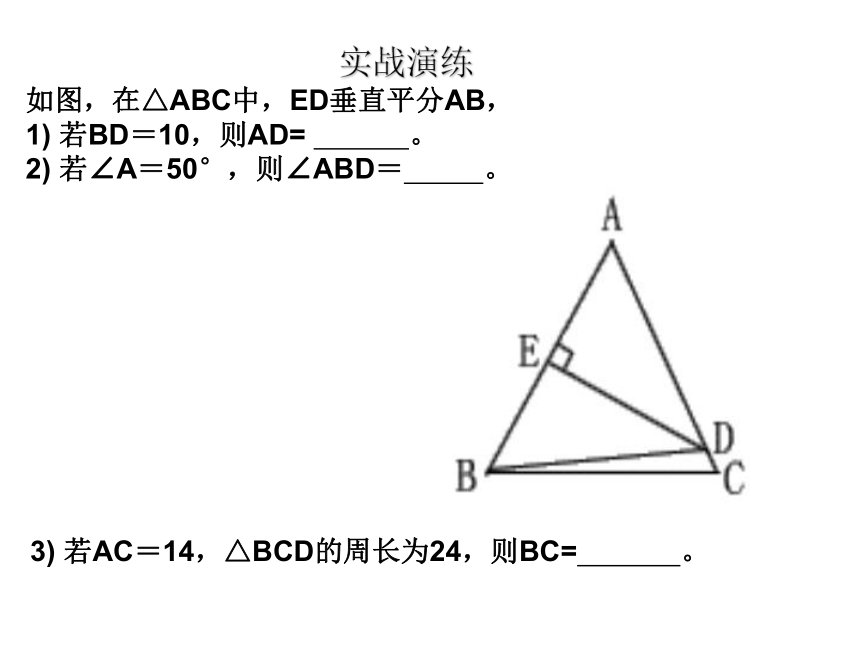
=9如图,在△ABC中,ED垂直平分AB,
1) 若BD=10,则AD= 。
2) 若∠A=50°,则∠ABD= 。3) 若AC=14,△BCD的周长为24,则BC= 。
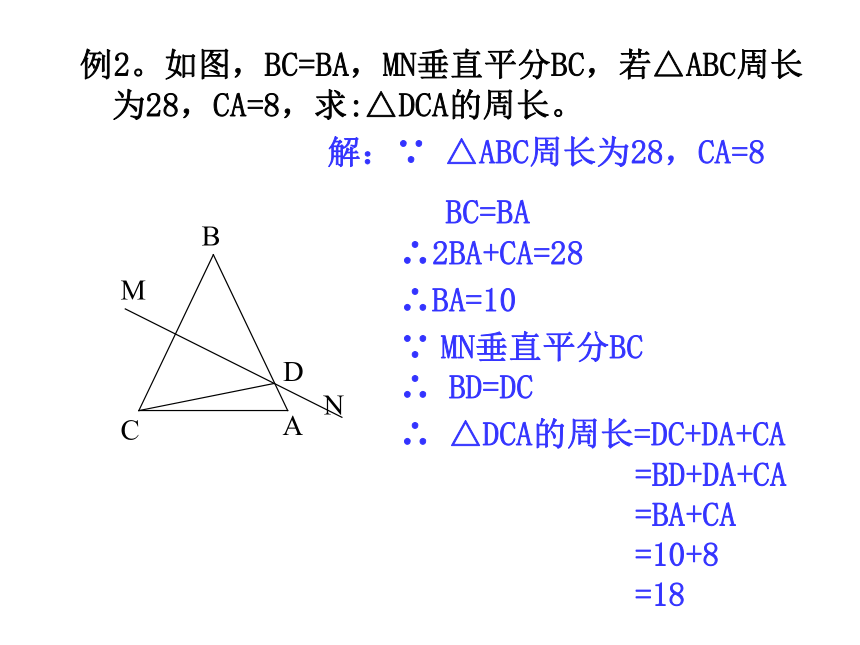
实战演练例2。如图,BC=BA,MN垂直平分BC,若△ABC周长为28,CA=8,求:△DCA的周长。BCADM解:∵ △ABC周长为28,CA=8
BC=BAN∴2BA+CA=28∴BA=10∵ MN垂直平分BC∴ BD=DC∴ △DCA的周长=DC+DA+CA
=BD+DA+CA
=BA+CA
=10+8
=18 例3。如图所示,直线MN和DE分别是线段AB、BC的垂直平分线,它们交于点O,试判断线段OA和OC是否相等?请说明理由?解:相等,连接OB.∵ MN是线段AB的垂直平分线(已知)∴ OA=OB(线段中垂线的性质)
又∵ DE是线段BC的垂直平分线
(已知)∴ OB=OC(线段中垂线的性质)∴ OA=OC(等量代换)课堂练习:
1。如图,PQ是线段DE、BC的中垂线,BD 与CE相等吗?为什么?2。如图,平面上有三个点A、B、C。你能否找到一个点P,使得PA=PB=PC?
泰安市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1ABL实际问题2 在104国道L(济南—泰安段)的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?104 国 道课后议练:
1。如图,在ΔABC中,DE是AC的垂直平分线,ΔABC与ΔABD的周长分别为18厘米和12厘米,求线段AE的长。
AB∟DCE课堂小结:
线段垂直平分线的性质及其运用
是本节课的重点,应用其性质我们可
以证明两条线段相等,也可对线段的
长度进行求解。直线MN垂直于线段AB,并且平分线段AB,我们把直线MN叫做线段AB的垂直平分线。
线段是轴对称图形,它的一条对称轴是这条线段的垂直平分线。
青岛版 《数学》八年级(上)2.4线段的垂直平分线
------(第1课时)1、能说出线段的垂直平分线的定理和逆定理,会区别运用这两个定理。
2、体会学习数学的方法,观察,概括,验证,比较等在本课时中的应用。
3、认识数学来源于生活,又服务于现实生活,体验数学的应用价值。教学目标PA=PBP1P1A=P1B……命题:线段垂直平分线上的点和这条线段两个端点的距离相等。由此你能得到什么规律?命题:线段垂直平分线上的点和这条线段两个端点的距离相等。C应用举例:
例1。如图所示,在ΔABC中,边BC的垂直平分线MN分别交AB于点M,交BC于点N, ΔBMC的周长为23,且BM=7,求BC的长。解:∵ MN是线段BC的垂直平分线
BM=7 ∴ CM=BM=7 ∵ ΔBMC 的周长=23∴BM+CM+BC=23∴BC=23-CM-BM
=23-7-7
=9如图,在△ABC中,ED垂直平分AB,
1) 若BD=10,则AD= 。
2) 若∠A=50°,则∠ABD= 。3) 若AC=14,△BCD的周长为24,则BC= 。
实战演练例2。如图,BC=BA,MN垂直平分BC,若△ABC周长为28,CA=8,求:△DCA的周长。BCADM解:∵ △ABC周长为28,CA=8
BC=BAN∴2BA+CA=28∴BA=10∵ MN垂直平分BC∴ BD=DC∴ △DCA的周长=DC+DA+CA
=BD+DA+CA
=BA+CA
=10+8
=18 例3。如图所示,直线MN和DE分别是线段AB、BC的垂直平分线,它们交于点O,试判断线段OA和OC是否相等?请说明理由?解:相等,连接OB.∵ MN是线段AB的垂直平分线(已知)∴ OA=OB(线段中垂线的性质)
又∵ DE是线段BC的垂直平分线
(已知)∴ OB=OC(线段中垂线的性质)∴ OA=OC(等量代换)课堂练习:
1。如图,PQ是线段DE、BC的中垂线,BD 与CE相等吗?为什么?2。如图,平面上有三个点A、B、C。你能否找到一个点P,使得PA=PB=PC?
泰安市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题1ABL实际问题2 在104国道L(济南—泰安段)的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?104 国 道课后议练:
1。如图,在ΔABC中,DE是AC的垂直平分线,ΔABC与ΔABD的周长分别为18厘米和12厘米,求线段AE的长。
AB∟DCE课堂小结:
线段垂直平分线的性质及其运用
是本节课的重点,应用其性质我们可
以证明两条线段相等,也可对线段的
长度进行求解。直线MN垂直于线段AB,并且平分线段AB,我们把直线MN叫做线段AB的垂直平分线。
线段是轴对称图形,它的一条对称轴是这条线段的垂直平分线。
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
