坐标平面上的直线[上学期]

坐标平面上的直线
数学是一种精神，一种理性的精神，正是这种精神，激发、促进、鼓舞并驱使人类的思维得以运用到最完善的程度。
――――克莱因
知识纵横
一般地，若y=kx+b(k,b是常数,k≠0)，则y叫做x的一次函数，它的图象是一条直线，函数解析式y=kx＋b中的系数符号，决定图象的大致位置及单调性(y随x的变化情况）．如图所示：
一次函数、二元一次方程、直线有着深刻的联系，任意一个一次函数y=kx+b都可看作是关于x，y的一个二元一次方程kx－y＋b=0；任意一个关于x，y的二元一次方程ax +by+c=O可化为形如的函数形式．坐标平面上的直线可以表示一次函数与二元一次方程，而使用方程和函数的思想可以研究直线位置关系，求坐标平面上的直线的交点坐标可转化为解由函数解析式联立的方程组．
例题求解
例1. （1）一次函数y=kx+3的图象与坐标轴的两个交点之间的距离为5，则k的值为___________.
(2005年黑龙江省中考题）
(2）在直角坐标系中，有四个点A(-8,3），B(-4,5),C(0,n),D(m,0)，当四边形ABCD的周长最短时，
则的值为_____。 （湖北省竞赛题）
思路点拨：对于(1),把直线与坐标轴交点坐标用k的代数式表示，用勾股定理建立k的方程；对于（2），AB的长度不变，只需使其余的三条线段的和最短，设法将折线拉直，不妨考虑运用对称的知识与方法．
［例2】设直线nx+ (n+1) y= (n为自然数）与两坐标轴围成的三角形面积为Sn(n=1，2，…2000)，则S1+S2+S2000的值为（ ）．
A. 1 B. C. D.
（河北省竞赛题）
思路点拨: 求出直线与x轴、Y轴的交点坐标，从一般形式人手，把Sn用含n的代数式表示．
【例3]甲、乙两名同学进行登山比赛，图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶的过程中，各自行进的路程随时间变化的图象，根据图象中的有关数据回答下列问题：
(1)分别求出表示甲、乙两同学登山过程中路程s（千米）与时间t(时）的函数解析式（不要求写出自变量t的取值范围）；
(2)当甲到达山顶时，乙行进到山路上的某点A处，求A点距山顶的距离；
(3)在(2)的条件下，设乙同学从A处继续登山，甲同学到达山顶后休息1小时，沿原路下山，在点B处与乙相遇，此时点B与山顶距离为1. 5千米，相遇后甲、乙各自按原来的路线下山和上山，求乙到达山顶时，甲离山脚的距离是多少千米？
(2005年哈尔滨市中考题）
思路点拨：对于（3），解题的关键是从图象获取信息，确定直线BD的解析式．
例题4．如图，在平面直角坐标系中，CA⊥x轴于点A(1, 0)，DB⊥x轴于点B (3，0)，直线CD与x轴,y轴分别交于点F, E,且解析式为y=kx＋3，s四边形ABDC = 4.
（1)求直线CD的解析式；
(2)试探索在x轴正半轴上存在几个点P，使△EPF为等腰三角形，并求出这些点的坐标．
(2005年包头市中考题）
思路点拨：对于（1),利用面积关系建立k的方程；对于(2),由于等腰三角形底未确定、应根据P点的位置分情况讨论．
例5. 如图，直线与x轴、Y轴分别交于点A、B，以线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC= 90o，如果在第二象限内有一点P（a, ），且△ABP的面积与△ABC的面积相等，求a的值．
（天津市竞赛题）
思路点拨：利用S△ABP＝ S△ABC，建立含a的方程，解题的突破口是把S△ABP表
示成有边落在坐标轴上的三角形面积的和差．
基础夯实
1.直线y= mx＋n如图所示，化简=________．
(2005年山西省中考题）
2. 如图，直线与X轴、Y轴分别交于点A和点B,M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点处，则直线AM的解析式为_______
(2005年重庆市中考题）
3. 点A为直线y=-2x+2上的一点, 点A到两坐标轴的距离相等，则点A的坐标为_______
(2004年无锡市中考题）
4. 已知abc≠0,并且.则直线y = px＋p一定通过_________象限．
(2004年镇江市中考题）
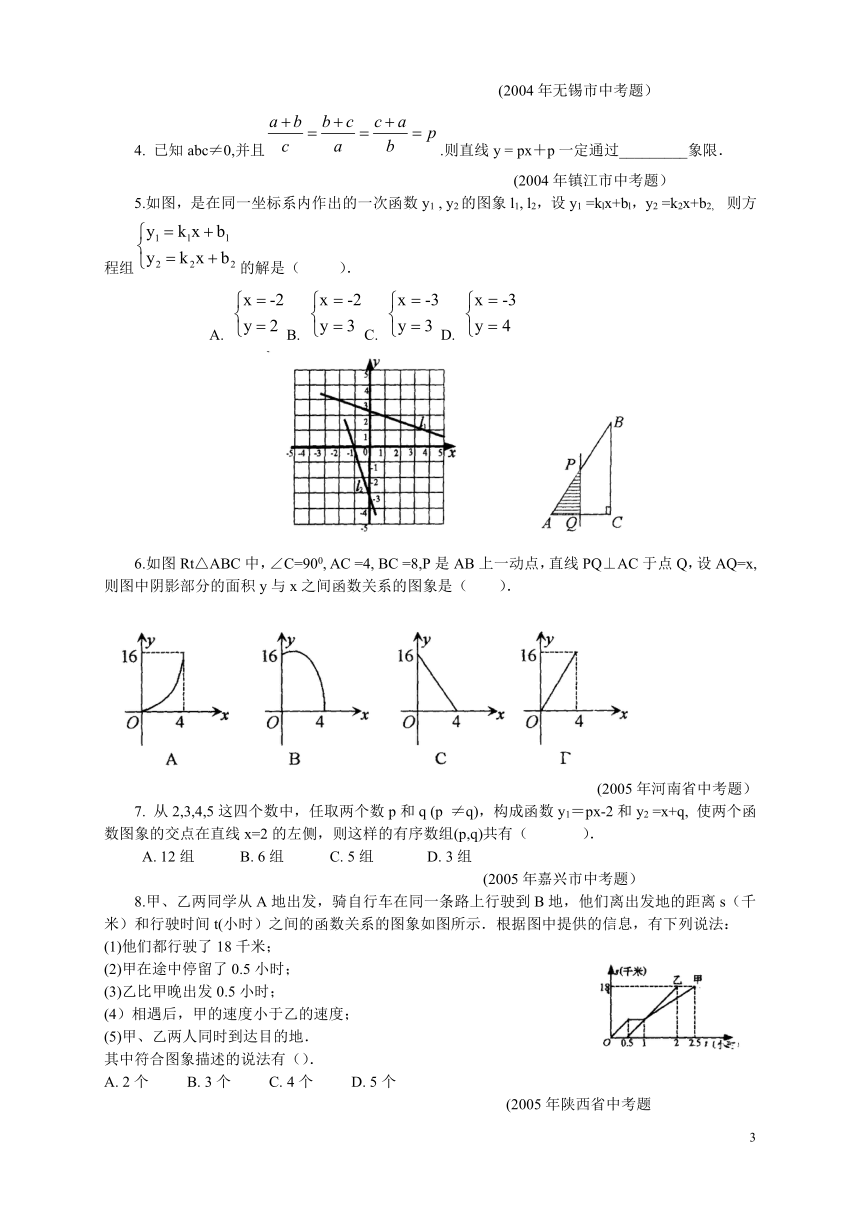
5.如图，是在同一坐标系内作出的一次函数y1 , y2的图象l1, l2，设y1 =klx+bl，y2 =k2x+b2, 则方程组的解是（ ）．
A. B. C. D.
6.如图Rt△ABC中，∠C=900, AC =4, BC =8,P是AB上一动点，直线PQ⊥AC于点Q，设AQ=x,则图中阴影部分的面积y与x之间函数关系的图象是（ ）．
(2005年河南省中考题）
7. 从2,3,4,5这四个数中，任取两个数p和q (p ≠q)，构成函数y1＝px-2和y2 =x+q, 使两个函数图象的交点在直线x=2的左侧，则这样的有序数组(p,q)共有（ ）．
A. 12组 B. 6组 C. 5组 D. 3组
(2005年嘉兴市中考题）
8.甲、乙两同学从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s（千米）和行驶时间t(小时）之间的函数关系的图象如图所示．根据图中提供的信息，有下列说法：
(1)他们都行驶了18千米；
(2)甲在途中停留了0.5小时；
(3)乙比甲晚出发0.5小时；
(4）相遇后，甲的速度小于乙的速度；
(5)甲、乙两人同时到达目的地．
其中符合图象描述的说法有（）．
A. 2个 B. 3个 C. 4个 D. 5个
(2005年陕西省中考题
9. 如图表示甲、乙两名选手在一次自行车越野赛中，路程y随时间x变化的图象（全程）．根据图象回答下列问题：
(1)求比赛开始多少分钟时，两人第一次相遇；
(2)求这次比赛全程是多少千米；
(3)求比赛开始多少分钟时，两人第二次相遇．
(2004年黑龙江省中考题）
10.春、秋季节，由于冷空气的人侵，地面气温急剧下降到00C以下的天气现象称为“霜冻”．由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害．
某种植物在气温是0℃以下持续时间超过3小时，即遭受霜冻灾害，需采取预防措施．如图是气象台某天发布的该地区气象信息，预报了次日0时~8时气温随时间变化情况，其中0时～5时，5时～8时的图象分别满足一次函数关系．请你根据图中信息，针对这种植物判断次日是否需要采取防霜冻措施，并说明理由．
(2005年宁夏中考题）
11.如图，一次函数y=kx+b的图象与x轴,y轴分别交于点A (6, 0)和B(0, )，线段AB的垂直平分线交x轴于点C，交AB于点D.
（1)求这个一次函数表达式；
(2)求点C的坐标．
(2005年无锡市中考题）
能力拓展
12.在直角坐标系中,x轴上的动点M(x,0)到定点P(5,5),Q(2,1)的距离分别为 MP和MQ ,那么当MP+ MQ取最小值时，点M的横坐标为_________
（全国初中数学竞赛题）
13. 如图，直线y= - 2x+ 6与x轴、y轴分别交于P，Q两点，把△POQ沿PQ翻折，点O落在R处，则点R的坐标是______
(江苏省竞赛题)
14.如图，在直角坐标系中，矩形OABC的顶点B的坐标为(15,6)，直线恰好将矩形OABC分为面积相等的两部分，则b=_______.
15.在直角坐标系中，横纵坐标都是整数的点称为整点，设k为整数，当直线y= x-3与y=kx+k的交点为整点时,k的值可以取（ ）个．
A. 2 B. 4 C. 6 D. 8
(2005年四川省竞赛题）
16. 如图，直线y=x和y=-x＋1把坐标平面分成I、II、III、IV 4个部分（包括边界在内），则满足 y≤x且y≥一x＋1的点（x，y）必在（ ）．
A.第I部分 B.第II部分 C.第III部分 D.第IV部分
（第19届江苏省竞赛题）
17.有一个装有进、出水管的容器，单位时间内进、出的水量都是一定的．已知容器的容积为600升，又知单开进水管10分钟可把空容器注满，若同时打开进、出水管,20分钟可把满容器的水放完．现已知水池内有水200升，先打开进水管5分钟，再打开出水管，两管同时开放直至把容器中的水放完．则能正确反映这一过程中容器的水量Q(升）随时间t(分钟）变化的图象是（ ）．
(2005年黄冈市中考题）
18.如图，△AOB为正三角形，点B坐标为(2，0)，过点C(一2，0)作直线l交AO于D，交AB于E，且使△ADE和△DCO的面积相等，求直线l的函数解析式．
（太原市竞赛题）
19. 如图，P是y轴上一动点，是否存在平行于y轴的直线x=t,使它与直线y=x和直线分别交于点D,E（E在D的上方），且△PDE为等腰直角三角形．若存在，求t的值及点P的坐标；若不存在，请说明理由．
(2005年大连市中考题）
综合创新
20. 在直角坐标系中，有以A(-1, -1），B(1，-1），C（1 ,l），D(-1,1）为顶点的正方形，设它在折线y= | x-a |+a上侧部分的面积为S，试求S关于a的函数关系式，并画出它们的图象．
（河北省竞赛题）
21.阅读：我们知道，在数轴上，x=1表示一个点，而在平面直角坐标系中，x=1表示一条直线；我们还知道，以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象，它也是一条直线，如图①. 观察图①可以得出：直线x=1与直线y = 2x +1的交点P的坐标（1,3)就是方程组的解，所以这个方程组的解为
在直角坐标系中，x≤1表示一个平面区域，即直线x=1以及它左侧的部分，如图②;y≤2x＋1也表示一个平面区域，即直线y=2x十1以及它下方的部分，如图③．
（第21题）
回答下列问题：
(1)在直角坐标系中，用作图象的方法求出方程组的解；
(2)用阴影表示所围成的区域；
（2005年陕西省中考题）
(3)求在直角坐标平面中不等式｜x｜＋｜y｜≤3围成的面积．
（第19届香港中学数学竟赛题）
已知点A（1，0）、B（3，0）、E（-4，0）F（0、2），动点C（x，y）在线段EF上运动，设三角形ABC的面积为y。求y关于x的函数关系式。（y=0.5x+2（－4PAGE
6