增长率的探索[上学期]
图片预览








文档简介
课件23张PPT。增长率问题探索(2)新阳中学 初三数学组情境创设市场经济不仅让我们走上了富裕之路,而且让我们学会了科学的经营方法。个体老板张明原计划按600元/套销售一批西服,但上市后销售不佳,为使资金正常运转,减少库存积压,张明将这批西服连续两次降价打折处理,调整价格到了384元。如果两次降价折扣相同,求每次降价率为多少?两次打折标示多少折?你能用我们学过的增长率解决这个问题吗?问题探究问题1:
阳江市市政府考虑在两年后实现是财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少?问题2:
某服装店花1200元进了一批服装,按40﹪的利润定价,无人购买,决定打折出售,但依然无人购买,结果又一次打折后才售完。经结算,这批服装共盈利280元。若两次打折相同,每次打了几折?思考猜想1、翻一番的含义与倍数之间的关系有什么联系和区别?
2、若问题1中调整计划,两年后的财政净收入为原值的1.5倍,1.2倍,----,那么两年中的平均年增长率相应的调整多少?
3、又若第二年的增长率为第一年的二倍,那么第一年的增长率为多少时可以实现市财政收入翻一番?
4、问题2中的打折销售与降低率之间的联系。探究点拨:
弄清翻一番和打折的含义,根据常见增长率问题的解法列出方程求解。发现规律:
1、翻一番的含义,即为原来的2倍,若设原财政收入为1,那么两年后的产值为2,设平均年增长率为x ,则可列方程(x+1)2=2.
2、若两年后的财政净收入值为原值的1.5倍、1.2倍、---a 倍等,则可分别通过列出方程(x+1)2=1.5,(x+1)2=1.2,(x+1)2=a,求出两年中的平均增长率x. 3、设第一年的增长率为x,若第二年的增长率为第一年的2倍,要想实现市财政净收入翻一番,则有方程(x+1)(2x+1)=2.4、先理解折的含义,如打八折即为原价的80﹪。也即相当于降价20﹪。设每次降价率为x ,则有1200×40﹪(1-x)2=280,求出x值,即知道每次打了几折。教材分析重点:翻番
翻一番表示为原量的2倍,翻两番表示为原量的4倍。
打折:
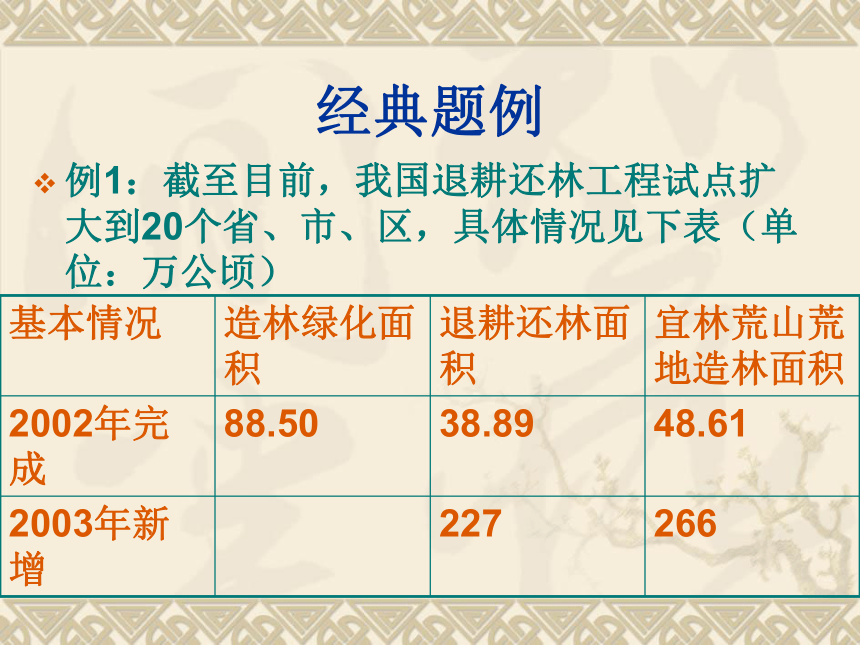
这是生活中的术语,如打八五折即为原来的85﹪。经典题例例1:截至目前,我国退耕还林工程试点扩大到20个省、市、区,具体情况见下表(单位:万公顷)(1)将上表补充完整;
(2)若2005年新增造林绿化面积比2003年新增造林绿化面积翻两番,2004、2005两年的平均增长率相同,求这个增长率。思路:由表可知:造林绿化面积=退耕还林面积+宜林荒山荒地造林面积。2005年新增造林绿化面积比2003年新增造林绿化面积翻两番即为4倍。可列方程求解。解:(1)表中数据为______.
(2)设这个增长率为x,依题意有:
493(1+x)2=493×4
解得:x1=1, x2=-3(不合题意,舍去)
∴x=1=100﹪.
答:这个增长率为100﹪.总结:正确理解翻两番的含义是解题的关键,应在日常生活中多接触类似术语的含义。随堂练习1、党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年(2001---2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是x,那么x满足的方程为( )
A、(1+x)2=2 B (1+x)2=4
C 1+2x=2 D (1+x)+2(1+x)=4例2:某工厂从今年一月起,每月生产收入是22万元,但在生产过程中会引起环境污染;若在按现状生产,将会受到环保部门的处罚,每月罚款2万元;如果投资111万元治理污染,治污系统可在一月份启用,这样该厂不但不受处罚,还可降低生产成本。使1至3月的生产收入以相同的百分率逐月增长。
经测算,投资治污后,一月份生产收入为25万元,1至3月份生产累计收入可达91万元;3月份以后,每月生产收入稳定在3月份的水平。(1)求出投资治污后2月、3月每月生产收入增长的百分率;(以下数据供参考:3.62=1.912,11.56=3.402)
(2)如果把利润看作是生产累计收入减去治理污染的投资额或环保部门的罚款额,试问治理污染多少个月后,所投资金开始见成效(即治污后所获利润不小于不治污情况下所获利润)?分析:首先必须弄清1至3月份生产累计是指3个月的生产总和;其次要明确治污前每月收入为(22-2)万元,若设经过n 个月后所投资金开始见效,则依据题意列出不等式求解。解:(1)设2月、3月每月增长的百分率为x,则有:
25+25(1+x)+25(1+x)2=91
整理得: X2+3x-0.64=0
解得: x1=0.2, x2=-3.2
因为增长率不能为负数,所以x=___.
答:2月、3月每月增长的百分率为____.(2)3月份的生产收入为:
25×(1+0.2)2=25×1.44=36(万元)
设治理污染n个月后,所投资金开始见成效,则有:
91+36(n-3)-111≥20n
解得: n≥____.
即投资治理污染____个月后见成效。 思考:
从这道题上,你认为在发展生产与保护环境问题上应坚持________观点,反对_______ 思想。着眼长远急功近利总结:解决此类问题的关键是熟悉增长率公式的应用,尤其注意在问(2)中应列不等式解题而不宜列成方程。随堂练习2、据2001年中国环境状况公报,我国由水蚀风蚀造成的水土流失面积达356万平方千米,某省重视水土流失问题,2001年治理了400平方千米,该省逐年加大治理力度,计划今明两年每年治理水土流失面积都比前一年增长一个相同的百分数,到2003年底,使这3年治理的水土流失面积达到1324平方千米。求该省今明两年治理水土流失面积每年增长的百分数。回眸引例市场经济不仅让我们走上了富裕之路,而且让我们学会了科学的经营方法。个体老板张明原计划按600元/套销售一批西服,但上市后销售不佳,为使资金正常运转,减少库存积压,张明将这批西服连续两次降价打折处理,调整价格到了384元。如果两次降价折扣相同,求每次降价率为多少?两次打折标示多少折?
解:设平均每次降价率为x ,根据题意得:
600(1-x)2=384
解得:x1= 1/5 x2= 9/5>1 (不合题意,舍去)
所以 x= 1/5 =20﹪,即每次降价率为20﹪。
第一次打折后价格为原价的1-x=80﹪,即打___折。
第二次打折后价格为原价的(1-x)2=64﹪,即打___折。
答:每次降价率为20﹪,第一次打___折,第二次打___折。
总结:求打折问题一般先求出降低率,再换算成折数。随堂练习:
3、一件上衣原价500元,第一次降价后,销售甚慢,第二次大幅度降价的百分率是第一次降价百分率的2倍,结果以每件240元的价格迅速售出,求每次应标价几折出售? 课堂回眸1.本节课你收获了哪些知识?
2.你能很熟练地运用增长率公式解决一些有关翻番和打折的问题吗?
3.解翻番和打折应用题容易出错的地方是-----? 作业:
P42 ——2
P44——5
阳江市市政府考虑在两年后实现是财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少?问题2:
某服装店花1200元进了一批服装,按40﹪的利润定价,无人购买,决定打折出售,但依然无人购买,结果又一次打折后才售完。经结算,这批服装共盈利280元。若两次打折相同,每次打了几折?思考猜想1、翻一番的含义与倍数之间的关系有什么联系和区别?
2、若问题1中调整计划,两年后的财政净收入为原值的1.5倍,1.2倍,----,那么两年中的平均年增长率相应的调整多少?
3、又若第二年的增长率为第一年的二倍,那么第一年的增长率为多少时可以实现市财政收入翻一番?
4、问题2中的打折销售与降低率之间的联系。探究点拨:
弄清翻一番和打折的含义,根据常见增长率问题的解法列出方程求解。发现规律:
1、翻一番的含义,即为原来的2倍,若设原财政收入为1,那么两年后的产值为2,设平均年增长率为x ,则可列方程(x+1)2=2.
2、若两年后的财政净收入值为原值的1.5倍、1.2倍、---a 倍等,则可分别通过列出方程(x+1)2=1.5,(x+1)2=1.2,(x+1)2=a,求出两年中的平均增长率x. 3、设第一年的增长率为x,若第二年的增长率为第一年的2倍,要想实现市财政净收入翻一番,则有方程(x+1)(2x+1)=2.4、先理解折的含义,如打八折即为原价的80﹪。也即相当于降价20﹪。设每次降价率为x ,则有1200×40﹪(1-x)2=280,求出x值,即知道每次打了几折。教材分析重点:翻番
翻一番表示为原量的2倍,翻两番表示为原量的4倍。
打折:
这是生活中的术语,如打八五折即为原来的85﹪。经典题例例1:截至目前,我国退耕还林工程试点扩大到20个省、市、区,具体情况见下表(单位:万公顷)(1)将上表补充完整;
(2)若2005年新增造林绿化面积比2003年新增造林绿化面积翻两番,2004、2005两年的平均增长率相同,求这个增长率。思路:由表可知:造林绿化面积=退耕还林面积+宜林荒山荒地造林面积。2005年新增造林绿化面积比2003年新增造林绿化面积翻两番即为4倍。可列方程求解。解:(1)表中数据为______.
(2)设这个增长率为x,依题意有:
493(1+x)2=493×4
解得:x1=1, x2=-3(不合题意,舍去)
∴x=1=100﹪.
答:这个增长率为100﹪.总结:正确理解翻两番的含义是解题的关键,应在日常生活中多接触类似术语的含义。随堂练习1、党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年(2001---2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是x,那么x满足的方程为( )
A、(1+x)2=2 B (1+x)2=4
C 1+2x=2 D (1+x)+2(1+x)=4例2:某工厂从今年一月起,每月生产收入是22万元,但在生产过程中会引起环境污染;若在按现状生产,将会受到环保部门的处罚,每月罚款2万元;如果投资111万元治理污染,治污系统可在一月份启用,这样该厂不但不受处罚,还可降低生产成本。使1至3月的生产收入以相同的百分率逐月增长。
经测算,投资治污后,一月份生产收入为25万元,1至3月份生产累计收入可达91万元;3月份以后,每月生产收入稳定在3月份的水平。(1)求出投资治污后2月、3月每月生产收入增长的百分率;(以下数据供参考:3.62=1.912,11.56=3.402)
(2)如果把利润看作是生产累计收入减去治理污染的投资额或环保部门的罚款额,试问治理污染多少个月后,所投资金开始见成效(即治污后所获利润不小于不治污情况下所获利润)?分析:首先必须弄清1至3月份生产累计是指3个月的生产总和;其次要明确治污前每月收入为(22-2)万元,若设经过n 个月后所投资金开始见效,则依据题意列出不等式求解。解:(1)设2月、3月每月增长的百分率为x,则有:
25+25(1+x)+25(1+x)2=91
整理得: X2+3x-0.64=0
解得: x1=0.2, x2=-3.2
因为增长率不能为负数,所以x=___.
答:2月、3月每月增长的百分率为____.(2)3月份的生产收入为:
25×(1+0.2)2=25×1.44=36(万元)
设治理污染n个月后,所投资金开始见成效,则有:
91+36(n-3)-111≥20n
解得: n≥____.
即投资治理污染____个月后见成效。 思考:
从这道题上,你认为在发展生产与保护环境问题上应坚持________观点,反对_______ 思想。着眼长远急功近利总结:解决此类问题的关键是熟悉增长率公式的应用,尤其注意在问(2)中应列不等式解题而不宜列成方程。随堂练习2、据2001年中国环境状况公报,我国由水蚀风蚀造成的水土流失面积达356万平方千米,某省重视水土流失问题,2001年治理了400平方千米,该省逐年加大治理力度,计划今明两年每年治理水土流失面积都比前一年增长一个相同的百分数,到2003年底,使这3年治理的水土流失面积达到1324平方千米。求该省今明两年治理水土流失面积每年增长的百分数。回眸引例市场经济不仅让我们走上了富裕之路,而且让我们学会了科学的经营方法。个体老板张明原计划按600元/套销售一批西服,但上市后销售不佳,为使资金正常运转,减少库存积压,张明将这批西服连续两次降价打折处理,调整价格到了384元。如果两次降价折扣相同,求每次降价率为多少?两次打折标示多少折?
解:设平均每次降价率为x ,根据题意得:
600(1-x)2=384
解得:x1= 1/5 x2= 9/5>1 (不合题意,舍去)
所以 x= 1/5 =20﹪,即每次降价率为20﹪。
第一次打折后价格为原价的1-x=80﹪,即打___折。
第二次打折后价格为原价的(1-x)2=64﹪,即打___折。
答:每次降价率为20﹪,第一次打___折,第二次打___折。
总结:求打折问题一般先求出降低率,再换算成折数。随堂练习:
3、一件上衣原价500元,第一次降价后,销售甚慢,第二次大幅度降价的百分率是第一次降价百分率的2倍,结果以每件240元的价格迅速售出,求每次应标价几折出售? 课堂回眸1.本节课你收获了哪些知识?
2.你能很熟练地运用增长率公式解决一些有关翻番和打折的问题吗?
3.解翻番和打折应用题容易出错的地方是-----? 作业:
P42 ——2
P44——5
