人教版数学七年级上册 1.2.4 有理数比较大小 教案
文档属性
| 名称 | 人教版数学七年级上册 1.2.4 有理数比较大小 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 48.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-26 11:42:51 | ||
图片预览


文档简介
课题 1.2.4有理数的大小比较
课型 新授课
教学目标:
1.知识与技能:进一步熟悉绝对值的概念,学会利用绝对值比较两个负数的大小,进而掌握比较有理数大小的一般方法。
2.过程与方法:通过数轴上认识绝对值的意义来比较两个负数的大小,培养学生利用旧知识建立新知识的化归能力。
3.情感态度与价值观:通过化归思想的培养,让学生养成全面分析的学习态度,更新数学知识。
教学重点:利用绝对值比较两个负数的大小.
教学 难点:利用绝对值比较两个异分母负分数的大小.
教学方法: 数形结合 探究交流
教具准备:三角尺、课件
教学过程:
问题引入
在小学里,我们已学会比较两个正数(或0)的大小,那么,引入负数以后,怎样比较两个有理数的大小呢 例如,1与-2哪个大 -1与0哪个大 -3与-4哪个大?
(引入新课,并板书课题。)
导入目标
1.通过探究得出有理数大小的比较方法.(重点)
2.能利用数轴及绝对值的知识,比较两个有理数的大小.
(难点)
新课
说一说
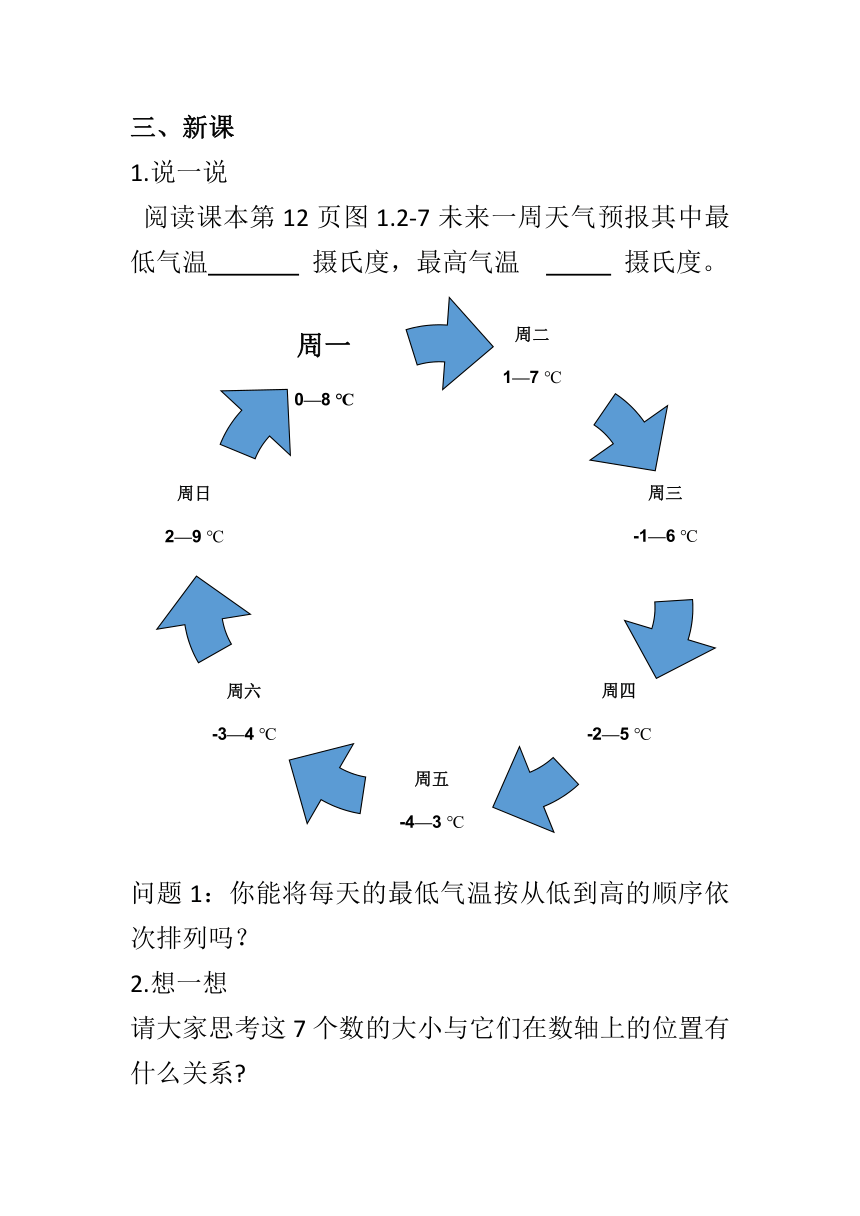
阅读课本第12页图1.2-7未来一周天气预报其中最低气温 摄氏度,最高气温 摄氏度。
(
周二
1—7
℃
周日
2—9
℃
周一
0—8 ℃
周六
-3—4
℃
周五
-4—3
℃
周四
-2—5
℃
周三
-1—6
℃
)
问题1:你能将每天的最低气温按从低到高的顺序依次排列吗?
2.想一想
请大家思考这7个数的大小与它们在数轴上的位置有什么关系
(
-4
-3 -2
-1 0
1 2
)
(
大小关系为:
-4 < -3< -2<-1< 0 <1 < 2
)
3.议一议
我们发现,在数轴上表示的两个数,右边的数总比左
边的数大.
(
例1
在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
(学生自主学习互查)
)
(
4
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
(数轴比较法)有没有更简单的方法?(绝对值比较法)
)
(
有理数的大小比较法则:
正数都大于零,负数都小于零,正数大于负数.
两个负数,绝对值大的反而小。
)
例2、比较下列各对数的大小:(师生共析)
(1)-(-1)和-(+2)
(2) 和
(3)-(-0.3)和
四.回味无穷
本节课你学会哪些知识?小组交流,谈谈自己的收获。
有理数大小比较的两种方法:
----利用数轴比较大小;
-----利用绝对值比较大小。
(
1、正数大于0, 0大于负数,正数大于负数。
)小结法则:
(
2、两个正数,绝对值大的正数大.
)
3、两个负数绝对值大的反而小.
作业
1.课本13页练习
2.习题1.2第6题7题。
六、板书设计
有理数的大小比较
1数轴比较法:数轴上右边的数大于左边的数
2法则比较法:正数都大于零,负数都小于零,正数大于负数;
两个负数,绝对值大的反而小。
3应用:例1
例2
4练习:
七、教学反思:
本节课联系小学及课本内容,把两个有理数的大小比较进行系统的概括,体验出两个有理数比较大小的方法。⑴利用数轴比较大小;⑵利用绝对值比较大小。本节课的教学目标是让学生掌握这两种方法。主要用到数形结合的思想方法。这节课的重点是利用绝对值比较两个负数的大小。难点是利用绝对值比较两个异分母负数大小;这是本节课较难的部分,为了解决难点,特别要让学生清楚地了解进行比较时的过程:⑴先求出两个负数的绝对值。⑵比较两个绝对值的大小(要通分,化为同分母分数)。⑶根据绝对值大的负数反而小的结论判断这两个负分数的大小。
上完这节课后,感觉到本节课还有不少地方设计得不好。结合实际,我的反思如下:
从学生完成的练习分析,学生对课本的知识掌握程度不错,能运用两种方法判断有理数的大小,但仍有不足之处:
⒈在教学中,过多地推理概括有理数比较大小的两种方法,缺少让学生发表自己意见,与同伴合作交流的机会较少。
2.教学的预见性还不够,时间控制的不好,学生练习时间不够充分。
3.学生对比较两个负分数的大小,感到比较困难。它既用到新学的两个负数比较大小的结论,又联系到两个分数比较大小的问题,学生往往只做一次比较,比较完两个绝对值的大小后,就得出结论了。只有根据课堂教学实际多进行反思,才能得到不断改进,不断提高。
课型 新授课
教学目标:
1.知识与技能:进一步熟悉绝对值的概念,学会利用绝对值比较两个负数的大小,进而掌握比较有理数大小的一般方法。
2.过程与方法:通过数轴上认识绝对值的意义来比较两个负数的大小,培养学生利用旧知识建立新知识的化归能力。
3.情感态度与价值观:通过化归思想的培养,让学生养成全面分析的学习态度,更新数学知识。
教学重点:利用绝对值比较两个负数的大小.
教学 难点:利用绝对值比较两个异分母负分数的大小.
教学方法: 数形结合 探究交流
教具准备:三角尺、课件
教学过程:
问题引入
在小学里,我们已学会比较两个正数(或0)的大小,那么,引入负数以后,怎样比较两个有理数的大小呢 例如,1与-2哪个大 -1与0哪个大 -3与-4哪个大?
(引入新课,并板书课题。)
导入目标
1.通过探究得出有理数大小的比较方法.(重点)
2.能利用数轴及绝对值的知识,比较两个有理数的大小.
(难点)
新课
说一说
阅读课本第12页图1.2-7未来一周天气预报其中最低气温 摄氏度,最高气温 摄氏度。
(
周二
1—7
℃
周日
2—9
℃
周一
0—8 ℃
周六
-3—4
℃
周五
-4—3
℃
周四
-2—5
℃
周三
-1—6
℃
)
问题1:你能将每天的最低气温按从低到高的顺序依次排列吗?
2.想一想
请大家思考这7个数的大小与它们在数轴上的位置有什么关系
(
-4
-3 -2
-1 0
1 2
)
(
大小关系为:
-4 < -3< -2<-1< 0 <1 < 2
)
3.议一议
我们发现,在数轴上表示的两个数,右边的数总比左
边的数大.
(
例1
在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
(学生自主学习互查)
)
(
4
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
(数轴比较法)有没有更简单的方法?(绝对值比较法)
)
(
有理数的大小比较法则:
正数都大于零,负数都小于零,正数大于负数.
两个负数,绝对值大的反而小。
)
例2、比较下列各对数的大小:(师生共析)
(1)-(-1)和-(+2)
(2) 和
(3)-(-0.3)和
四.回味无穷
本节课你学会哪些知识?小组交流,谈谈自己的收获。
有理数大小比较的两种方法:
----利用数轴比较大小;
-----利用绝对值比较大小。
(
1、正数大于0, 0大于负数,正数大于负数。
)小结法则:
(
2、两个正数,绝对值大的正数大.
)
3、两个负数绝对值大的反而小.
作业
1.课本13页练习
2.习题1.2第6题7题。
六、板书设计
有理数的大小比较
1数轴比较法:数轴上右边的数大于左边的数
2法则比较法:正数都大于零,负数都小于零,正数大于负数;
两个负数,绝对值大的反而小。
3应用:例1
例2
4练习:
七、教学反思:
本节课联系小学及课本内容,把两个有理数的大小比较进行系统的概括,体验出两个有理数比较大小的方法。⑴利用数轴比较大小;⑵利用绝对值比较大小。本节课的教学目标是让学生掌握这两种方法。主要用到数形结合的思想方法。这节课的重点是利用绝对值比较两个负数的大小。难点是利用绝对值比较两个异分母负数大小;这是本节课较难的部分,为了解决难点,特别要让学生清楚地了解进行比较时的过程:⑴先求出两个负数的绝对值。⑵比较两个绝对值的大小(要通分,化为同分母分数)。⑶根据绝对值大的负数反而小的结论判断这两个负分数的大小。
上完这节课后,感觉到本节课还有不少地方设计得不好。结合实际,我的反思如下:
从学生完成的练习分析,学生对课本的知识掌握程度不错,能运用两种方法判断有理数的大小,但仍有不足之处:
⒈在教学中,过多地推理概括有理数比较大小的两种方法,缺少让学生发表自己意见,与同伴合作交流的机会较少。
2.教学的预见性还不够,时间控制的不好,学生练习时间不够充分。
3.学生对比较两个负分数的大小,感到比较困难。它既用到新学的两个负数比较大小的结论,又联系到两个分数比较大小的问题,学生往往只做一次比较,比较完两个绝对值的大小后,就得出结论了。只有根据课堂教学实际多进行反思,才能得到不断改进,不断提高。
