北师大版九年级数学上册试题 1.3正方形的性质与判定同步练习(含答案)
文档属性
| 名称 | 北师大版九年级数学上册试题 1.3正方形的性质与判定同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 406.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-26 13:15:11 | ||
图片预览



文档简介
1.3正方形的性质与判定同步练习
第一课时
一、选择题
1.如图,正方形ABCD中,点E是CD边上一点,连接AE,交对角线BD于点F,连接CF,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
2.矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分一组对角
3.如图,四边形ABCD中,AD=DC,,,若四边形ABCD面积为,则DE的长为( )
A. B. C. D.
4.若正方形的对角线长为2 cm,则这个正方形的面积为( )
A.4 B.2 C. D.
5.如图,在正方形中,,E为对角线上与A,C不重合的一个动点,过点E作于点F,于点G,连接.下列结论:
①;②;③;④的最小值为3.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
6.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A.1,4,5 B.2,3,5 C.3,4,5 D.2,2,4
7.如图,正方形ABCD中,点E是CD边上一点,连接AE,交对角线BD于点F,连接CF,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
8.如图,正方形ABCD的边长为7,在各边上顺次截取,则四边形EFGH的面积为( ).
A.20 B.25 C.30 D.35
9.如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为( )
A.4 B. C. D.2
二、填空题
1.2300多年前,我国古代名著《墨经》中有这样的记载:“圆,一中同长也.”因此,古代就知道把车轮设计成圆形,如果车轮是正方形,将边长为1米的正方形滚动一周,那么正方形中心的轨迹长为_________米.
2.边长为的正方形的对角线的长度为______.
3.将边长为3的正方形ABCD绕点C顺时针方向旋转45°到FECG的位置(如图),EF与AD相交于点H,则HD的长为___.(结果保留根号)
4.如图,E是正方形ABCD的对角线BD上一点,连接CE,过点E作,垂足为点F.若,,则正方形ABCD的面积为___.
5.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是___________.
6.如图,四边形ABCD是边长为5的正方形,∠CEB和∠CFD都是直角且点C,E,F三点共线,BE=2,则阴影部分的面积是 _____.
7.如图所示,大正方形ABCD内有一小正方形DEFG,对角线DF长为6 cm,已知小正方形DEFG向东北方向平移3 cm就得到正方形D'E'BG',则大正方形ABCD的面积为____.
三、解答题
1.如图,大正方形与小正方形的面积之差是,求阴影部分的面积.
2.如图,在正方形中,点在边的延长线上,点在边的延长线上,且,连接和相交于点.
求证: .
3.如图 ,已知点 C 为线段 AB 上一点,四边形ACMF、BCNE 是两个正方形.求证:AN=BM
4.如图,E是正方形的边上任意一点(不与点A,B重合),按逆时针方向旋转后恰好能够与重合.
(1)旋转中心是________,旋转角为________;
(2)请你判断的形状,并说明理由.
5.在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于F,当∠BED=120°时,求∠EFD的度数.
【中小学教辅资源店 微信:mlxt2022】
第二课时
一、选择题
1.已知四边形是平行四边形,下列结论中不正确的是( )
A.当时,四边形是正方形
B.当时,四边形是菱形
C.当时,四边形是菱形
D.当时,四边形是矩形
2.下列命题中,真命题是( )
A.有两个内角是的四边形是矩形 B.一组邻边互相垂直的菱形是正方形
C.对角线相互垂直的梯形是等腰梯形D.两组内角相等的四边形是平行四边形
3.已知四边形是平行四边形,,相交于点O,下列结论错误的是( )
A.,
B.当时,四边形是菱形
C.当时,四边形是矩形
D.当且时,四边形是正方形
4.如图,在四边形中,,,,交于点.添加一个条件使这个四边形成为一种特殊的平行四边形,则以下说法错误的是( )
A.添加“”,则四边形是菱形
B.添加“”,则四边形是矩形
C.添加“”,则四边形是菱形
5D.添加“”,则四边形是正方形
5.如图,在菱形中,对角线,相交于点,只需添加一个条件,即可证明菱形是正方形,这个条件可以是( )
A. B. C. D.
二、填空题
1.如图,四边形是菱形,与相交于点,添加一个条件:________,可使它成为正方形.
2.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是_____.
3.在平面直角坐标系中,直线与x轴,y轴分别交于A,B,直线与x轴,y轴分别交于C,D其中,M,N均为线段AB上任意两点,P,Q为线段CD上任意两点,记点M,N,P,Q组成的四边形为图形G.
下列四个结论中,
① 对于任意的k,都存在无数个图形G是平行四边形;
② 对于任意的k,都存在无数个图形G是矩形;
③ 存在唯一的k,使得此时有一个图形G是菱形;
④ 至少存在一个k,使得此时有一个图形G是正方形
所有正确结论的序号是__________.
三、解答题
1.已知:如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,DE//AC,CE//AD,连接BE,CD.求证:四边形CDBE是正方形.
2.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,E是CD的中点,过点C作CF∥AB,交AE的延长线于点F,连接BF.
(1)求证:四边形BDCF是菱形;
(2)直接写出当Rt△ABC满足什么条件时,四边形BDCF是正方形.
3.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
4.已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:;
(2)连接AC,DE,当 四边形ACED是正方形?请说明理由.
第一课时答案
一、选择题
C.B.C.B.C.B.C.BD.
二、填空题
1..
2.2.
3.3﹣3.
4.196.
5.22.5°.
6..
7. cm2
三、解答题
1.
解:设大正方形的边长为a,小正方形的边长为b,
故阴影部分的面积是:AE BC+AE BD=AE(BC+BD)
=(AB﹣BE)(BC+BD)
=(a﹣b)(a+b)
=(a2﹣b2)
=×50
=25.
故阴影部分的面积为25.
2.
证明:∵四边形ABCD为正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°,
又∵CE=DF,
∴CE+BC=DF+CD即BE=CF,
在△BCF和△ABE中,
∴(SAS),
∴AE=BF.
3.∵四边形ACMF和四边形CBEN都是正方形,
∴AC=CM, NC =BC,∠ACN=∠BCM=90°,
∴△ACN≌△MCB(SAS),
∴AN=BM.
4.解:由题意得:旋转中心是点D;旋转角为∠ADC,
在正方形ABCD中,∠ADC=90°,
∴旋转角为90°;
故答案为:点D;90°
(2)
解:根据题意得:,,
∴是等腰直角三角形.
5.(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ECB=∠ECD=45°.
∴在△BEC与△DEC中,
∴△BEC≌△DEC(SAS).
(2)解:∵△BEC≌△DEC,
∴∠BEC=∠DEC=∠BED,
∵∠BED=120°,
∴∠BEC=60°=∠AEF.
∴∠EFD=60°+45°=105°.
第二课时答案
一、选择题
A.B.B.B.A
二、填空题
1.
2.①③④.
3.①②④
三、解答题
1.证明:∵DE∥AC,CE∥AD,
∴四边形ADEC是平行四边形,
∴DE=AC,CE=AD,
∵AD=DB,
∴CE=DB,
∵CE∥DB,
∴四边形CDBE是平行四边形,
∵AC=BC,
∴BC=DE,
∴平行四边形DBEC是矩形,
∵∠ACB=90°,
∴CD=AD=DB,
∴矩形CDBE是正方形.
∴四边形CDBE是正方形.
2.解:(1)∵CF∥AB
∴∠CFA=∠BAF,∠ADC=∠FCD,且CE=DE
∴△CEF≌△DEA(AAS)
∴CF=AD,
∵CD是Rt△ABC的中线
∴CD=AD=BD
∴CF=BD,且CF∥AB
∴四边形BDCF是平行四边形,且CD=BD
∴四边形BDCF是菱形
(2)当AC=BC时,四边形BDCF是正方形,
理由如下:∵AC=BC,CD是中线
∴CD⊥AB,且四边形BDCF是菱形
∴四边形BDCF是正方形.
3.证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
4.解:(1)∵四边形ABCD是平行四边形
∴AD∥BE
∴∠ADO=∠ECO
又∵O是CD的中点
∴OD=OC
在△AOD和△EOC中
∴△AOD ≌ △EOC (ASA)
(2)45°
由(1)知,OA=OE,OC=OD
∴四边形ACED是平行四边形
∴AD=CE
又∵四边形ABCD是平行四边形
∴AD=BC
∴BC =CE
当∠B=∠AEB=45°时,
且
∴四边形ACED是正方形.
第一课时
一、选择题
1.如图,正方形ABCD中,点E是CD边上一点,连接AE,交对角线BD于点F,连接CF,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
2.矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分一组对角
3.如图,四边形ABCD中,AD=DC,,,若四边形ABCD面积为,则DE的长为( )
A. B. C. D.
4.若正方形的对角线长为2 cm,则这个正方形的面积为( )
A.4 B.2 C. D.
5.如图,在正方形中,,E为对角线上与A,C不重合的一个动点,过点E作于点F,于点G,连接.下列结论:
①;②;③;④的最小值为3.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
6.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A.1,4,5 B.2,3,5 C.3,4,5 D.2,2,4
7.如图,正方形ABCD中,点E是CD边上一点,连接AE,交对角线BD于点F,连接CF,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
8.如图,正方形ABCD的边长为7,在各边上顺次截取,则四边形EFGH的面积为( ).
A.20 B.25 C.30 D.35
9.如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为( )
A.4 B. C. D.2
二、填空题
1.2300多年前,我国古代名著《墨经》中有这样的记载:“圆,一中同长也.”因此,古代就知道把车轮设计成圆形,如果车轮是正方形,将边长为1米的正方形滚动一周,那么正方形中心的轨迹长为_________米.
2.边长为的正方形的对角线的长度为______.
3.将边长为3的正方形ABCD绕点C顺时针方向旋转45°到FECG的位置(如图),EF与AD相交于点H,则HD的长为___.(结果保留根号)
4.如图,E是正方形ABCD的对角线BD上一点,连接CE,过点E作,垂足为点F.若,,则正方形ABCD的面积为___.
5.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是___________.
6.如图,四边形ABCD是边长为5的正方形,∠CEB和∠CFD都是直角且点C,E,F三点共线,BE=2,则阴影部分的面积是 _____.
7.如图所示,大正方形ABCD内有一小正方形DEFG,对角线DF长为6 cm,已知小正方形DEFG向东北方向平移3 cm就得到正方形D'E'BG',则大正方形ABCD的面积为____.
三、解答题
1.如图,大正方形与小正方形的面积之差是,求阴影部分的面积.
2.如图,在正方形中,点在边的延长线上,点在边的延长线上,且,连接和相交于点.
求证: .
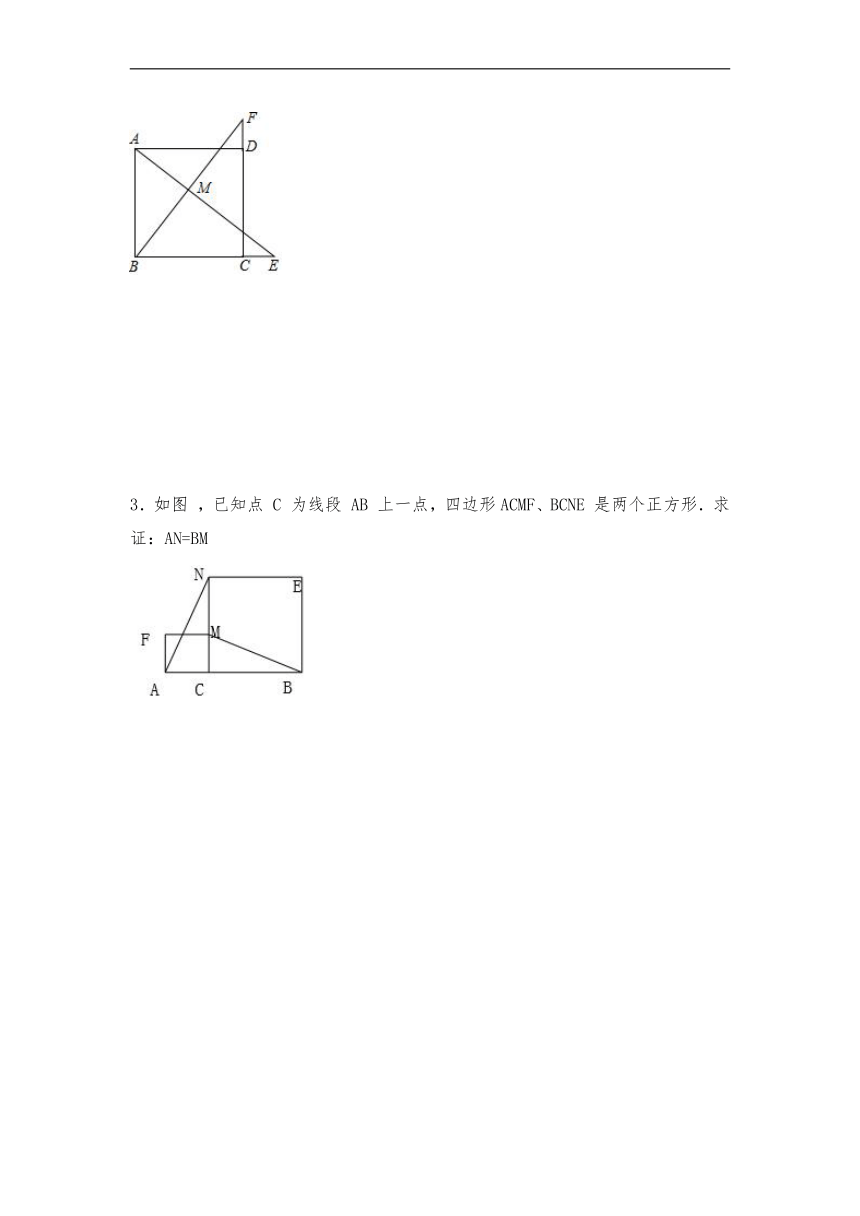
3.如图 ,已知点 C 为线段 AB 上一点,四边形ACMF、BCNE 是两个正方形.求证:AN=BM
4.如图,E是正方形的边上任意一点(不与点A,B重合),按逆时针方向旋转后恰好能够与重合.
(1)旋转中心是________,旋转角为________;
(2)请你判断的形状,并说明理由.
5.在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于F,当∠BED=120°时,求∠EFD的度数.
【中小学教辅资源店 微信:mlxt2022】
第二课时
一、选择题
1.已知四边形是平行四边形,下列结论中不正确的是( )
A.当时,四边形是正方形
B.当时,四边形是菱形
C.当时,四边形是菱形
D.当时,四边形是矩形
2.下列命题中,真命题是( )
A.有两个内角是的四边形是矩形 B.一组邻边互相垂直的菱形是正方形
C.对角线相互垂直的梯形是等腰梯形D.两组内角相等的四边形是平行四边形
3.已知四边形是平行四边形,,相交于点O,下列结论错误的是( )
A.,
B.当时,四边形是菱形
C.当时,四边形是矩形
D.当且时,四边形是正方形
4.如图,在四边形中,,,,交于点.添加一个条件使这个四边形成为一种特殊的平行四边形,则以下说法错误的是( )
A.添加“”,则四边形是菱形
B.添加“”,则四边形是矩形
C.添加“”,则四边形是菱形
5D.添加“”,则四边形是正方形
5.如图,在菱形中,对角线,相交于点,只需添加一个条件,即可证明菱形是正方形,这个条件可以是( )
A. B. C. D.
二、填空题
1.如图,四边形是菱形,与相交于点,添加一个条件:________,可使它成为正方形.
2.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是_____.
3.在平面直角坐标系中,直线与x轴,y轴分别交于A,B,直线与x轴,y轴分别交于C,D其中,M,N均为线段AB上任意两点,P,Q为线段CD上任意两点,记点M,N,P,Q组成的四边形为图形G.
下列四个结论中,
① 对于任意的k,都存在无数个图形G是平行四边形;
② 对于任意的k,都存在无数个图形G是矩形;
③ 存在唯一的k,使得此时有一个图形G是菱形;
④ 至少存在一个k,使得此时有一个图形G是正方形
所有正确结论的序号是__________.
三、解答题
1.已知:如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,DE//AC,CE//AD,连接BE,CD.求证:四边形CDBE是正方形.
2.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,E是CD的中点,过点C作CF∥AB,交AE的延长线于点F,连接BF.
(1)求证:四边形BDCF是菱形;
(2)直接写出当Rt△ABC满足什么条件时,四边形BDCF是正方形.
3.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
4.已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:;
(2)连接AC,DE,当 四边形ACED是正方形?请说明理由.
第一课时答案
一、选择题
C.B.C.B.C.B.C.BD.
二、填空题
1..
2.2.
3.3﹣3.
4.196.
5.22.5°.
6..
7. cm2
三、解答题
1.
解:设大正方形的边长为a,小正方形的边长为b,
故阴影部分的面积是:AE BC+AE BD=AE(BC+BD)
=(AB﹣BE)(BC+BD)
=(a﹣b)(a+b)
=(a2﹣b2)
=×50
=25.
故阴影部分的面积为25.
2.
证明:∵四边形ABCD为正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°,
又∵CE=DF,
∴CE+BC=DF+CD即BE=CF,
在△BCF和△ABE中,
∴(SAS),
∴AE=BF.
3.∵四边形ACMF和四边形CBEN都是正方形,
∴AC=CM, NC =BC,∠ACN=∠BCM=90°,
∴△ACN≌△MCB(SAS),
∴AN=BM.
4.解:由题意得:旋转中心是点D;旋转角为∠ADC,
在正方形ABCD中,∠ADC=90°,
∴旋转角为90°;
故答案为:点D;90°
(2)
解:根据题意得:,,
∴是等腰直角三角形.
5.(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ECB=∠ECD=45°.
∴在△BEC与△DEC中,
∴△BEC≌△DEC(SAS).
(2)解:∵△BEC≌△DEC,
∴∠BEC=∠DEC=∠BED,
∵∠BED=120°,
∴∠BEC=60°=∠AEF.
∴∠EFD=60°+45°=105°.
第二课时答案
一、选择题
A.B.B.B.A
二、填空题
1.
2.①③④.
3.①②④
三、解答题
1.证明:∵DE∥AC,CE∥AD,
∴四边形ADEC是平行四边形,
∴DE=AC,CE=AD,
∵AD=DB,
∴CE=DB,
∵CE∥DB,
∴四边形CDBE是平行四边形,
∵AC=BC,
∴BC=DE,
∴平行四边形DBEC是矩形,
∵∠ACB=90°,
∴CD=AD=DB,
∴矩形CDBE是正方形.
∴四边形CDBE是正方形.
2.解:(1)∵CF∥AB
∴∠CFA=∠BAF,∠ADC=∠FCD,且CE=DE
∴△CEF≌△DEA(AAS)
∴CF=AD,
∵CD是Rt△ABC的中线
∴CD=AD=BD
∴CF=BD,且CF∥AB
∴四边形BDCF是平行四边形,且CD=BD
∴四边形BDCF是菱形
(2)当AC=BC时,四边形BDCF是正方形,
理由如下:∵AC=BC,CD是中线
∴CD⊥AB,且四边形BDCF是菱形
∴四边形BDCF是正方形.
3.证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
4.解:(1)∵四边形ABCD是平行四边形
∴AD∥BE
∴∠ADO=∠ECO
又∵O是CD的中点
∴OD=OC
在△AOD和△EOC中
∴△AOD ≌ △EOC (ASA)
(2)45°
由(1)知,OA=OE,OC=OD
∴四边形ACED是平行四边形
∴AD=CE
又∵四边形ABCD是平行四边形
∴AD=BC
∴BC =CE
当∠B=∠AEB=45°时,
且
∴四边形ACED是正方形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
