数学人教A版(2019)必修第一册5.1.2 弧度制 课件(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.2 弧度制 课件(共25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-26 07:10:36 | ||
图片预览








文档简介
(共25张PPT)
5.1 任意角和弧度制
5.1.2 弧度制
第五章 三角函数
学习目标
1.了解弧度制,体会引入弧度制的必要性.
2.理解1弧度的角及弧度的定义.
3.掌握角度与弧度的换算公式,能进行角度与弧度的换算,并熟记几个特殊角的弧度数.
4.掌握弧度制中扇形的弧长公式和面积公式.
重点:了解弧度制,并能进行弧度与角度的换算.
难点:弧度的概念.
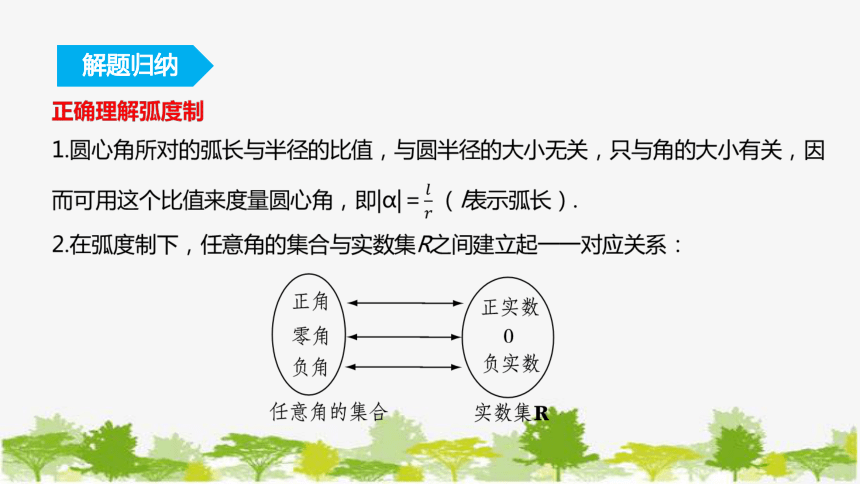
知识梳理
一、角度制、弧度制的相关概念
角度制
1弧度
一般地,正角的弧度数是一个 ,负角的弧度数是一个 ,
零角的弧度数是 .
正数
二、角度与弧度的换算
负数
0
弧度与角度换算公式:
如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对
值是|α|= .
例1
一 弧度制的概念的理解
常考题型
在大小不同的圆中,1 rad的圆心角所对的 ( )
A.弦长相等 B.弧长相等
C.弦长等于所在圆的半径 D.弧长等于所在圆的半径
【解析】 由弧度制的定义,1弧度的角就是所对弧长与半径之比等于1的角,所以1 rad的圆心角所对的弧长等于所在圆的半径.
【答案】 D
解题归纳
训练题
2.[2020·上海市行知中学高一检测]一场数学科目考试需要两个小时,则时针走了 弧度.
例2
二 角度与弧度的互化
角度与弧度的换算公式
角度化弧度 弧度化角度
360°=2π rad 2π rad=360°
180°=π rad π rad=180°
解题归纳
训练题
1.
2.
-105°
D
三 弧度制下终边相同的角的表示及其应用
例3
将-1 125°表示成2kπ+α(k∈Z,0≤α<2π)的形式,并在[-4π,0)上找出与角-1 125°终边相同的角.
【解题提示】 先把-1 125°化成k·360°+α(k∈Z)的形式,再用弧度制表示.
解题归纳
训练题
1.
2.
3.
4.
解题归纳
四 与弧长、扇形面积有关的问题
例4
解题归纳
训练题
[2020·黑龙江大庆市第十中学高一期末]已知扇形的半径为2,圆心角为2弧度,则该扇形的面积为 .
1.
2.
[2020·安徽省太和县第一中学高一期末]已知一扇形的面积是8 cm2,周长是12 cm,则该扇形的圆心角α(0<α<π)的弧度数是 .
解题归纳
小结
1.角度与弧度的换算
2.弧长公式、扇形面积公式
角度制 弧度制
弧长 公式
扇形 面积 公式
5.1 任意角和弧度制
5.1.2 弧度制
第五章 三角函数
学习目标
1.了解弧度制,体会引入弧度制的必要性.
2.理解1弧度的角及弧度的定义.
3.掌握角度与弧度的换算公式,能进行角度与弧度的换算,并熟记几个特殊角的弧度数.
4.掌握弧度制中扇形的弧长公式和面积公式.
重点:了解弧度制,并能进行弧度与角度的换算.
难点:弧度的概念.
知识梳理
一、角度制、弧度制的相关概念
角度制
1弧度
一般地,正角的弧度数是一个 ,负角的弧度数是一个 ,
零角的弧度数是 .
正数
二、角度与弧度的换算
负数
0
弧度与角度换算公式:
如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对
值是|α|= .
例1
一 弧度制的概念的理解
常考题型
在大小不同的圆中,1 rad的圆心角所对的 ( )
A.弦长相等 B.弧长相等
C.弦长等于所在圆的半径 D.弧长等于所在圆的半径
【解析】 由弧度制的定义,1弧度的角就是所对弧长与半径之比等于1的角,所以1 rad的圆心角所对的弧长等于所在圆的半径.
【答案】 D
解题归纳
训练题
2.[2020·上海市行知中学高一检测]一场数学科目考试需要两个小时,则时针走了 弧度.
例2
二 角度与弧度的互化
角度与弧度的换算公式
角度化弧度 弧度化角度
360°=2π rad 2π rad=360°
180°=π rad π rad=180°
解题归纳
训练题
1.
2.
-105°
D
三 弧度制下终边相同的角的表示及其应用
例3
将-1 125°表示成2kπ+α(k∈Z,0≤α<2π)的形式,并在[-4π,0)上找出与角-1 125°终边相同的角.
【解题提示】 先把-1 125°化成k·360°+α(k∈Z)的形式,再用弧度制表示.
解题归纳
训练题
1.
2.
3.
4.
解题归纳
四 与弧长、扇形面积有关的问题
例4
解题归纳
训练题
[2020·黑龙江大庆市第十中学高一期末]已知扇形的半径为2,圆心角为2弧度,则该扇形的面积为 .
1.
2.
[2020·安徽省太和县第一中学高一期末]已知一扇形的面积是8 cm2,周长是12 cm,则该扇形的圆心角α(0<α<π)的弧度数是 .
解题归纳
小结
1.角度与弧度的换算
2.弧长公式、扇形面积公式
角度制 弧度制
弧长 公式
扇形 面积 公式
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
