数学七年级下暑假培优专题训练1(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
数学七年级下暑假培优专题训练
专题一、相交线、平行线
【专题导航】
目录
【考点一 对顶角邻补角的判断】............................................1
【考点二 垂线的性质】....................................................5
【考点三 三线八角】.....................................................7
【考点四 平行线】.......................................................10
【聚焦考点1】
知识点一、相交线
直线的位置关系:在同一平面内,不重合的两条直线之间的位置关系只有两种:相交或平行。
1.对顶角的概念:①两个角有公共顶点;②两个角的边互为反向延长线
2.邻补角的概念 ①两个角有公共顶点; ② 有一条公共边;③另一边互为反向延长线
3.对顶角的性质:对顶角相等
4.邻补角的性质:邻补角互补
【典例剖析1】
【考点一 对顶角邻补角的判断】
【典例1-1】当光线从空气中射入某种液体中时,光线的传播方向发生了变化,在物理学中这种现象叫做光的折射.如图,液面MN于点D,一束光线沿CD射入液面,在点D处发生折射,折射光线为DE,点F为CD的延长线上一点,若入射角,折射角,则的度数为( )
A.14° B.16° C.18° D.25°
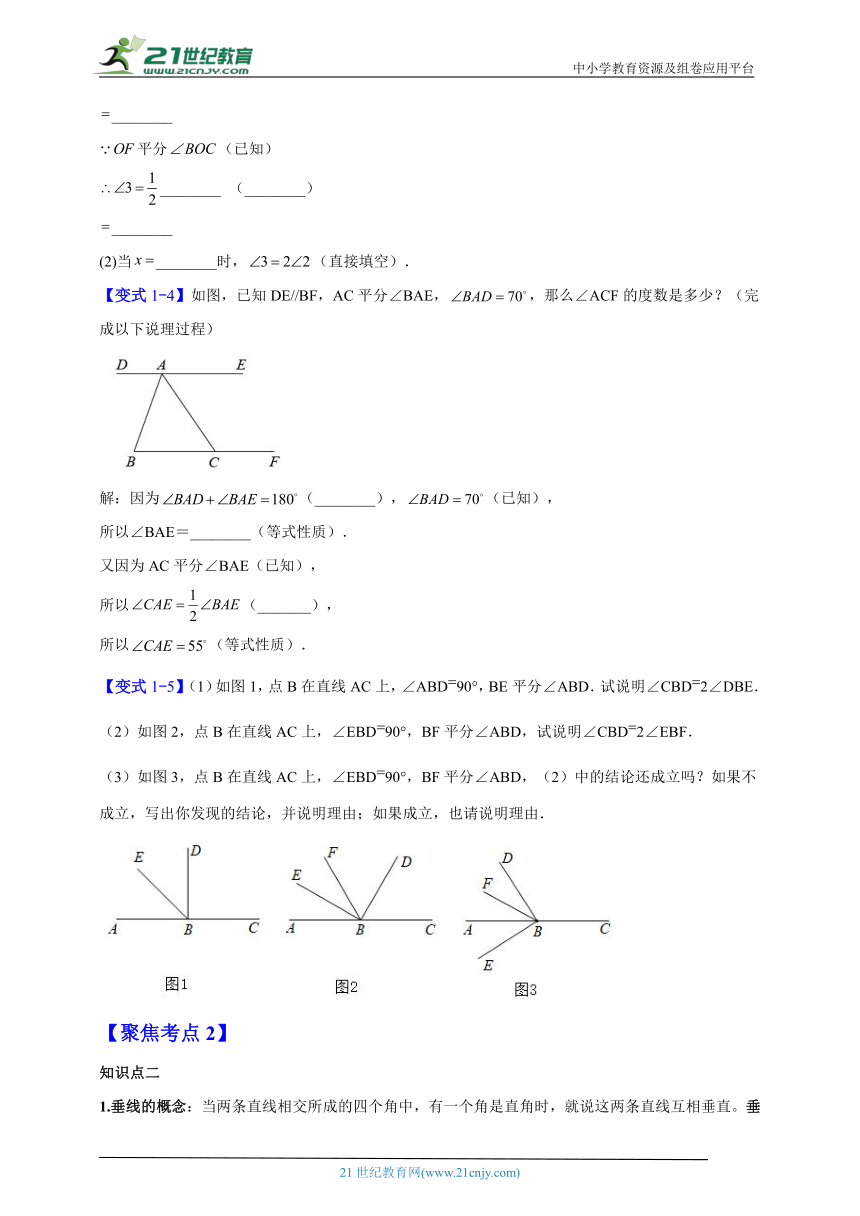
【典例1-2】如图,是一座正八边形古塔,某数学兴趣小组的同学想知道这个正八边形古塔的一个内角的度数,在不能进入塔内测量的情况下,设计了如图所示的测量方案:①反向延长正八边形内角∠AOB的两边,得到∠COD;②测量∠COD的度数.则∠COD的度数即为正八边形古塔内角∠AOB的度数.其中的数学原理是( )
A.邻补角互补 B.对顶角相等 C.同位角相等 D.内错角相等
【典例1-3】(1)如图(1),已知直线a、b相交于点 O,则(1)图中共有几对对顶角 几对邻补角?
(2)如图(2),已知直线a、b、c、d是经过点O的四条直线,则图(2)中共有几对对顶角(不含平角) 几对邻补角?
针对训练1
【变式1-1】如图,直线CD,EF相交于点O,射线OA在∠COF的内部,∠DOF=∠AOD.
(1)如图1,若∠AOC=120°,求∠EOC的度数;
(2)如图2,若∠AOC=α(60°<α<180°),将射线OA绕点O逆时针旋转60°,到OB,
①求∠EOB的度数(用含α的式子表示);
②观察①中的结果,直接写出∠AOC,∠EOB之间的数量关系.
(3)如图3 ,0°<∠AOC <120°,将射线OA绕点O顺时针旋转60°,到OB,请直接写出∠AOC,∠EOB之间的数量关系.
【变式1-2】如图,直线AB、EF相交于点D,∠ADC=90°.
(1)∠2的余角有 ; ,理由是 ;
(2)若∠1与∠2的度数之比为1:3,求∠CDF的度数,请完成填空:
设∠1的度数为,所以∠2= °(用表示),因为∠ADC=90°,所以∠1+∠2= °(用表示)=90°.所以∠1= °,所以∠2= °,所以∠CDF= °.
【变式1-3】如图,直线相交于点O,,平分,.
(1)当时,求的度数(填空完成下列说理过程);
解: (已知)
________
________(邻补角定义)
________
平分(已知)
________ (________)
________
(2)当________时,(直接填空).
【变式1-4】如图,已知DE//BF,AC平分∠BAE,,那么∠ACF的度数是多少?(完成以下说理过程)
解:因为(________),(已知),
所以∠BAE=________(等式性质).
又因为AC平分∠BAE(已知),
所以(_______),
所以(等式性质).
【变式1-5】(1)如图1,点B在直线AC上,∠ABD90°,BE平分∠ABD.试说明∠CBD2∠DBE.
(2)如图2,点B在直线AC上,∠EBD90°,BF平分∠ABD,试说明∠CBD2∠EBF.
(3)如图3,点B在直线AC上,∠EBD90°,BF平分∠ABD,(2)中的结论还成立吗?如果不成立,写出你发现的结论,并说明理由;如果成立,也请说明理由.
【聚焦考点2】
知识点二
1.垂线的概念:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足,如下图,AB⊥CD,垂足为点O。
2.垂线的基本性质:
① 经过一点有且只有一条直线垂直于已知直线;
② 连接直线外一点与直线上各点的所有线段中,垂线段最短;
③ 从直线外一点到直线的垂线段的长度,叫做点到直线的距离。
3. 垂线的画法
过一点画已知直线的垂线有两种方法:一是用三角板,二是用量角器。有这两种工具时,应掌握“一靠二过三画”这一要领。
【典例剖析2】
【考点二 垂线的性质】
【典例2-1】如图,直线相交于点O,平分,求的度数.
【典例2-2】作图:(使用铅笔作图,保留作图痕迹)
如图,外有一点,画出点到三角形三边的垂线分别交于点、、.
【典例2-3】如图,在直角三角形中,,,.请解答下列问题:
(1)点B到的距离是 ,点A到的距离是 ;
(2)请在图中作出点C到的垂线段;
(3) (填“”、“”、“”),理由是 .
针对训练2
【变式2-1】如图,的三个顶点A、B、C在正方形网格中,每个小方格的边长都为1.请在方格纸上画图并回答下列问题:
(1)过C点画直线的垂线,垂足为点E;
(2)过A点画射线,交直线于点F;
(3)点C到直线的距离为线段___________的长度;
(4)比较大小:线段___________线段(填“>”、“”或“=”).
【变式2-2】如图,直线外有一点,点都在直线上,,已知,,,,则点到直线的距离是_________.
【聚焦考点3】
知识点三、三线八角
如下图,直线AB、CD被直线EF所截,形成的独立的角有八个,简称为“三线八角”。
1.同位角“F”:没有公共顶点的两个角,它们在直线AB,CD的同侧,在第三条直线EF的同旁(即位置相同,如∠1和∠8分别在AB、CD的上方且在EF的右侧),这样的一对角叫做同位角。
2.内错角“Z””/N”:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的两旁(即位置交错,如∠4和∠5都在AB、CD之间,EF的两侧),这样的一对角叫做内错角。
3.同旁内角“U”:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的同旁(如∠3和∠5都在AB、CD之间,EF的两侧),这样的一对角叫做同旁内角。
注:1.这三类角都是成对出现的;
2.这三类角必须是两条直线被第三条直线所截形成的;
3.每对角没有公共的顶点
【典例剖析3】
【考点三 三线八角】
【典例3-1】据说中国最早的风筝是由古代哲学家墨翟制作的.如图风筝的骨架构成了多种位置关系的角.下列角中与∠1构成同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
【典例3-2】如图,在三角形所在平面内画一条直线,使得与成同旁内角的角有3个.若与成同旁内角的角有4个,则该怎样画这条直线?
【典例3-3】如图,在直角三角形中,若斜边为,两直角边分别为,,设,,.
(1)试用所学知识说明:斜边是最长的边;
(2)试用所学知识说明:;
(3)试化简.
针对训练3
【变式3-1】如图所示.
(1)与,与,与各是什么角,是哪两条直线被哪一条直线所截得的?
(2)的内错角有哪些?
(3)写出直线,被所截得的同旁内角,直线,被所截得的同旁内角.
【变式3-2】如图.在图中,
(1)同位角共__对,内错角共__对,同旁内角共__对;
(2)与是____,它们是_____被___截成的;
(3)与中_____被_____所截而得到的角;
(4)和被所截而成的内错角是_______,同旁内角是_______.
【变式3-3】与是直线______ 、______ 被直线______ 所截得的______ ;(填序号)
(①,②,③,④,⑤,⑥同位角,⑦内错角,⑧同旁内角)
【聚焦考点4】
知识点四
平行线
1.平行线的概念:①在同一平面内, ②不相交的两条直线叫做平行线。
平行线用符号“∥”表示,如:直线与直线互相平行,记作∥,读作a平行于b。
2.平行线画法:过直线外一点画已知直线的平行线,可按“一落,二靠,三移,四画”四步操作,如图
3. 平行公理及其推论
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
推论:如果两条直线都与第三条直线平行,那么这两直线也互相平行。简称平行于同一条直线的两条直线也互相平行。用符号语言表示为:∵a∥b, c∥b ∴a∥c
【典例剖析4】
【考点四 平行线】
【典例4-1】数学活动课上,小亮把两个含30°角的三角板按照如图所示方式摆放,点,,,在同一条直线上,他让小明判断直线与的位置关系,小明很快说出了答案并讲出了判断的依据.请你猜猜小明的答案和理由.
【典例4-2】作图题:如图,在平面内有不共线的3个点A,B,C.
(1)作射线BA,在BA延长线上取一点E,使AE=AB;
(2)作线段BC并延长BC到点F,使CF=BC;
(3)连接AC,EF;
(4)度量线段AC和EF的长度,直接写出二者之间的数量关系_______,观察AC和FE的位置是 (填“平行”或“相交”)关系;
(5)作BC的中点D,连接AD,猜想S三角形ABD S三角形ACD(填“>”“=”或“<”).
【典例4-3】在同一平面内,任意三条直线有哪几种不同的位置关系?你能画图说明吗?
下面是小明的解题过程:
解:有两种位置关系,如图:
你认为小明的解答正确吗?如果不正确,请你给出正确的解答.
针对训练4
【变式4-1】(1)观察如图所示的长方体后填空
用符号表示下列两棱的位置关系:
A1B1____AB ,AA1____AB ,
A1D1____C1D1 , AD____BC;
(2)A1B1与BC所在的直线是两条不相交的直线,他们_ ___平行线(填“是”或“不是”).由此可知,在__________,两条不相交的直线才能叫平行线.
(3)在同一平面内,两条不重合的直线位置关系只有_____种,即_____________.
【变式4-2】下列三种说法:
①相等的角是对顶角.
②若线段AB与线段CD没有交点,则ABCD.
③若a、b、c都是直线,且ab,bc,则a与c不相交.
正确的是 _____.
数学七年级下暑假培优专题训练
专题一、相交线(解析版)
【典例剖析】
【考点一 对顶角邻补角的判断】
【典例1-1】当光线从空气中射入某种液体中时,光线的传播方向发生了变化,在物理学中这种现象叫做光的折射.如图,液面MN于点D,一束光线沿CD射入液面,在点D处发生折射,折射光线为DE,点F为CD的延长线上一点,若入射角,折射角,则的度数为( )
A.14° B.16° C.18° D.25°
【答案】A
【分析】根据对顶角相等,计算角的差即可;
【详解】解:∵F点在CD延长线上,
∴∠1=∠FDB=50°,
∴∠EDF=∠FDB-∠2=14°,
故选: A.
【点睛】本题考查了对顶角的概念:有一个公共顶点,且一个角的两条边分别是另一个角的两条边的反向延长线,那么这两个角就叫做对顶角.
【典例1-2】如图,是一座正八边形古塔,某数学兴趣小组的同学想知道这个正八边形古塔的一个内角的度数,在不能进入塔内测量的情况下,设计了如图所示的测量方案:①反向延长正八边形内角∠AOB的两边,得到∠COD;②测量∠COD的度数.则∠COD的度数即为正八边形古塔内角∠AOB的度数.其中的数学原理是( )
A.邻补角互补 B.对顶角相等 C.同位角相等 D.内错角相等
【答案】B
【分析】根据对顶角相等解答即可.
【详解】根据对顶角相等可知:∠AOB=∠COD;
故选:B
【点睛】本题考查的是对顶角,掌握对顶角相等是解题的关键.
【典例1-3】(1)如图(1),已知直线a、b相交于点 O,则(1)图中共有几对对顶角 几对邻补角?
(2)如图(2),已知直线a、b、c、d是经过点O的四条直线,则图(2)中共有几对对顶角(不含平角) 几对邻补角?
【答案】(1)2对对顶角,4对邻补角;(2)图中共有12对对顶角,24对邻补角
【分析】(1)根据对顶角、邻补角的定义判断即可;
(2)先将图(2)拆分成如图的形式,再根据(1)的结论判断即可.
【详解】解:(1)根据题图可知,图中共有2对对顶角,4对邻补角;
(2)将图(2)拆分为下图:
通过观察图形.不难发现a、b、c、d四条直线两两相交,最多有6个交点,而由(1)知:每个交点处有两对对顶角,有四对邻补角,
对顶角的对数:(对);邻补角的对数:(对);
答:图中共有12对对顶角,24对邻补角;
【点睛】本题考查了对顶角、邻补角的定义;仔细观察图形弄清各个角之间的对顶角关系和邻补角关系是解题的关键.
针对训练1
【变式1-1】如图,直线CD,EF相交于点O,射线OA在∠COF的内部,∠DOF=∠AOD.
(1)如图1,若∠AOC=120°,求∠EOC的度数;
(2)如图2,若∠AOC=α(60°<α<180°),将射线OA绕点O逆时针旋转60°,到OB,
①求∠EOB的度数(用含α的式子表示);
②观察①中的结果,直接写出∠AOC,∠EOB之间的数量关系.
(3)如图3 ,0°<∠AOC <120°,将射线OA绕点O顺时针旋转60°,到OB,请直接写出∠AOC,∠EOB之间的数量关系.
【答案】(1)∠EOC=20°;
(2)①∠EOB=;②∠EOB=∠AOC;
(3)当0°<∠AOC ≤90°时,∠EOB=∠AOC+120°;当90°<∠AOC ≤120°时,∠EOB=240°-∠AOC.
【分析】(1)根据补角的定义求出∠AOD,结合已知求出∠DOF,然后根据对顶角相等得出答案;
(2)①根据补角的定义求出∠AOD,结合已知求出∠DOF,然后根据对顶角相等求出∠EOC,再根据∠BOC=α-60°,求出∠EOB的度数即可;②根据题意结合补角的定义求出∠AOD=180°-∠AOC,∠BOC=∠AOC-60°,然后可得∠DOF=∠AOD=60°-∠AOC,再根据对顶角相等计算得出答案;
(3)分情况讨论:①当0°<∠AOC ≤90°时,根据题意结合补角的定义求出∠AOD=180°-∠AOC,∠BOC=∠AOC+60°,然后可得∠DOF=∠AOD=60°-∠AOC,再根据对顶角相等计算得出答案;②当90°<∠AOC ≤120°时,根据题意结合补角的定义求出∠AOD=180°-∠AOC,∠BOC=∠AOC+60°,然后可得∠DOF=∠AOD=60°-∠AOC,再根据对顶角相等计算得出∠EOC+∠BOC=∠AOC+120°,最后根据周角的定义计算得出答案.
【详解】(1)解:∵∠AOC=120°,
∴∠AOD=180°-∠AOC=180°-120°=60°,
∴∠DOF=∠AOD=20°,
∴∠EOC=∠DOF=20°;
(2)解:①∵∠AOC=α,
∴∠AOD=180°-α,
∴∠DOF=∠AOD=60°-,
∴∠EOC=∠DOF=60°-,
由题意得:∠AOB=60°,
∴∠BOC=α-60°,
∴∠EOB=∠EOC+∠BOC=60°-+α-60°=;
②观察①中结果可得:∠EOB=,
证明:∵∠AOD=180°-∠AOC,∠BOC=∠AOC-∠AOB=∠AOC-60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOB=∠EOC+∠BOC=60°-∠AOC+∠AOC-60°=∠AOC;
(3)解:①当0°<∠AOC ≤90°时,
如图,∵∠AOD=180°-∠AOC,∠BOC=∠AOC+∠AOB=∠AOC+60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOB=∠EOC+∠BOC=60°-∠AOC+∠AOC+60°=∠AOC+120°.
②当90°<∠AOC ≤120°时,
如图,∵∠AOD=180°-∠AOC,∠BOC=∠AOC+∠AOB=∠AOC+60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOC+∠BOC=60°-∠AOC+∠AOC+60°=∠AOC+120°,
∴∠EOB=360°-(∠EOC+∠BOC)=360°-∠AOC-120°=240°-∠AOC.
【点睛】本题考查了补角的定义,角的和差计算,对顶角相等,理清各角之间的关系是正确计算的前提.
【变式1-2】如图,直线AB、EF相交于点D,∠ADC=90°.
(1)∠2的余角有 ; ,理由是 ;
(2)若∠1与∠2的度数之比为1:3,求∠CDF的度数,请完成填空:
设∠1的度数为,所以∠2= °(用表示),因为∠ADC=90°,所以∠1+∠2= °(用表示)=90°.所以∠1= --°,所以∠2=---- °,所以∠CDF= -----°.
【答案】(1)∠1和∠BDF;∠BDF,同角的余角相等 ;(2)3x °,4x °,22.5 °,67.5 °,112.5 °.
【分析】(1)根据对顶角的定义以及余角的定义填空;
(2)根据题意,补充完整解题过程即可.
【详解】解:如图,因为直线AB、EF相交于点D,∠ADC=90°,
(1)∠2的余角有∠1和∠BDF;∠BDF,理由是 同角的余角相等 ;
(2)设∠1的度数为,所以∠2= 3x °(用表示),
因为∠ADC=90°,
所以∠1+∠2= 4x °(用表示)=90°.
所以∠1= 22.5 °,所以∠2= 67.5 °,
所以∠CDF= 112.5 °.
【点睛】本题考查了对顶角的定义,余角和补角,熟记概念并准确识图是解题的关键.
【变式1-3】如图,直线相交于点O,,平分,.
(1)当时,求的度数(填空完成下列说理过程);
解: (已知)
________
________(邻补角定义)
________
平分(已知)
________ (________)
________
(2)当________时,(直接填空).
【答案】(1),,,,角平分线定义,
(2)
【分析】(1)先根据平角的定义求出,再根据邻补角的定义求出,即可根据角平分线的定义求出的度数;
(2)同(1)推理过程求出,,再由,建立方程求解即可.
【详解】(1)解: (已知)
,
(邻补角定义)
,
平分(已知)
(角平分线的定义)
,
故答案为:,,,,角平分线定义,;
(2)解:,,
,
,
平分(已知)
,
∵,
∴,
解得
∴当时,,
故答案为:.
【点睛】本题主要考查了几何图形中角度的计算,角平分线的定义,灵活运用所学知识是解题的关键.
【变式1-4】如图,已知DE//BF,AC平分∠BAE,,那么∠ACF的度数是多少?(完成以下说理过程)
解:因为(________),(已知),
所以∠BAE=________(等式性质).
又因为AC平分∠BAE(已知),
所以(_______),
所以(等式性质).
【答案】邻补角的定义;110°;角平分线的定义.
【分析】根据邻补角的定义可得∠BAE=110°,由角平分线的定义得出∠CAE=BAE,即可得出结果.
【详解】解:因为∠BAD+∠BAE=180°(邻补角的定义),∠BAD=70°(已知),
所以∠BAE=110°(等式性质),
又因为AC平分∠BAE(已知),
所以∠CAE=BAE(角平分线的定义),
所以∠CAE=55°(等式性质).
故答案为:邻补角的定义;110°;角平分线的定义.
【点睛】题目主要考查邻补角的定义及角平分线的定义,理解这两个定义是解题关键.
【变式1-5】(1)如图1,点B在直线AC上,∠ABD90°,BE平分∠ABD.试说明∠CBD2∠DBE.
(2)如图2,点B在直线AC上,∠EBD90°,BF平分∠ABD,试说明∠CBD2∠EBF.
(3)如图3,点B在直线AC上,∠EBD90°,BF平分∠ABD,(2)中的结论还成立吗?如果不成立,写出你发现的结论,并说明理由;如果成立,也请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)成立,理由见解析
【分析】(1)分别求解 从而可得结论;
(2)先证明可得再利用等量代换可得结论;
(3)设 求解 再求解 从而可得结论.
【详解】解:(1) 点B在直线AC上,∠ABD90°,
BE平分∠ABD,
(2) 点B在直线AC上,∠EBD90°,
BF平分∠ABD,
即
(3)成立,理由见解析:
设 而BF平分∠ABD,
∠EBD90°,
【点睛】本题考查的是与余角和补角有关的计算,角平分线的定义,熟练的运用角的和差运算是解本题的关键.
【考点二 垂线的性质】
【典例2-1】如图,直线相交于点O,平分,求的度数.
【答案】
【分析】先根据垂直的定义得到,则,根据角平分线的定义得到,则由平角的定义可得.
【详解】解:∵,
∴,
∵,
∴,
∵平分,
∴,
∴.
【点睛】本题主要考查了几何图形中角度的计算,垂直的定义,角平分线的定义,灵活运用所学知识是解题的关键.
【典例2-2】作图:(使用铅笔作图,保留作图痕迹)
如图,外有一点,画出点到三角形三边的垂线分别交于点、、.
【答案】见解析
【分析】根据题意,过点分别作的垂线,垂足分别为,
【详解】解:如图所示,过点分别作的垂线,垂足分别为,则即为所求
【点睛】本题考查了作垂线,熟练掌握基本作图是解题的关键.
【典例2-3】如图,在直角三角形中,,,.请解答下列问题:
(1)点B到的距离是 ,点A到的距离是 ;
(2)请在图中作出点C到的垂线段;
(3) (填“”、“”、“”),理由是 .
【答案】(1)8,6
(2)见解析
(3)
【分析】(1)根据点到直线的距离的定义求解;
(2)过点作的垂线,垂足为;
(3)根据垂线段最短进行判断.
【详解】(1)解:点B到的距离是,点A到的距离是;
故答案为:8,6;
(2)如图,为所作;
(3),理由是垂线段最短.
故答案为:;垂线段最短.
【点睛】本题考查了点到直线的距离,垂线段最短,熟练掌握点到直线距离的概念是解答本题的关键.直线外一点到这条直线的垂线段的长度,叫做这个点到这条直线的距离.
针对训练2
【变式2-1】如图,的三个顶点A、B、C在正方形网格中,每个小方格的边长都为1.请在方格纸上画图并回答下列问题:
(1)过C点画直线的垂线,垂足为点E;
(2)过A点画射线,交直线于点F;
(3)点C到直线的距离为线段___________的长度;
(4)比较大小:线段___________线段(填“>”、“”或“=”).
【答案】(1)见解析
(2)见解析
(3)
(4)
【分析】(1)根据网格的特点作图即可;
(2)根据网格的特点作图即可;
(3)根据点到直线的距离的概念解答;
(4)根据垂线段最短解答.
【详解】(1)如图,直线即为所作;
(2)如图,射线即为所作;
(3)点C到直线的距离为线段的长度;
故答案为:;
(4)根据垂线段最短得:线段线段;
故答案为:.
【点睛】本题考查了利用网格作图、垂线段最短以及点到直线的距离等知识,熟练掌握相关知识是解题的关键.
【变式2-2】如图,直线外有一点,点都在直线上,,已知,,,,则点到直线的距离是_________.
【答案】4
【分析】直线外一点到直线的垂线段的长度,叫做点到直线的距离,由此即可得到答案.
【详解】解:直线外一点到直线的垂线段的长度,叫做点到直线的距离,,
点到直线的距离是4,
故答案为:4.
【点睛】本题考查点到直线的距离,关键是掌握点到直线的距离的定义.
【考点三 三线八角】
【典例3-1】据说中国最早的风筝是由古代哲学家墨翟制作的.如图风筝的骨架构成了多种位置关系的角.下列角中与∠1构成同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
【答案】A
【分析】根据同位角的定义解答.两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【详解】解:由图可得,与构成同位角的是.
故选:A.
【点睛】本题主要考查了同位角的定义,解题的关键是明确同位角的边构成“”形,内错角的边构成“”形,同旁内角的边构成“”形.
【典例3-2】如图,在三角形所在平面内画一条直线,使得与成同旁内角的角有3个.若与成同旁内角的角有4个,则该怎样画这条直线?
【答案】见解析
【分析】根据同旁内角的定义进行画图即可:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
【详解】解:如图1所示,与成同旁内角的角有共3个;
如图2所示,与成同旁内角的角有共4个.
【点睛】本题主要考查了同旁内角的定义,熟知相关定义是解题的关键.
【典例3-3】如图,在直角三角形中,若斜边为,两直角边分别为,,设,,.
(1)试用所学知识说明:斜边是最长的边;
(2)试用所学知识说明:;
(3)试化简.
【答案】(1),,中,斜边最长
(2)
(3)
【分析】(1)利用垂线段最短即可确定出,,的长短关系,问题即可解答;
(2)由两点之间,线段最短,即可得到结论成立;
(3)由三角形三边关系可以得到,结合(1)即可去掉绝对值号,然后合并同类项解答题目.
【详解】(1)解:因为是点C到直线AB的垂线段,
所以.
因为AB是点B到直线AC的垂线段,所以,
故,,中,斜边最长.
(2)解:因为点C与点B之间,BC是线段,而是折线,根据“两点之间,线段最短”,可得,即.
(3)解:∵,,,
∴,,,
∴原式.
【点睛】本题考查垂线段最短,两点间线段最短及绝对值化简问题,侧重考查知识点的记忆、理解、应用能力,解题的关键是掌握垂线段最短及两点间线段最短.
针对训练3
【变式3-1】如图所示.
(1)与,与,与各是什么角,是哪两条直线被哪一条直线所截得的?
(2)的内错角有哪些?
(3)写出直线,被所截得的同旁内角,直线,被所截得的同旁内角.
【答案】(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据同位角概念解答即可;
(2)根据内错的概念解答即可;
(3)根据同旁内角的概念解答即可.
【详解】(1)解:与是直线、被直线所截形成的同位角,
与是直线、被直线所截形成的同位角,
与是直线、被直线所截形成的同位角;
(2)解:当直线与被所截时,与是内错角,
当直线和被所截时,与是内错角;
(3)解:直线,被所截得的同旁内角有与,
直线,被所截得的同旁内角与.
【点睛】本题考查了同位角、内错角、同旁内角,解本题的关键要抓住各类角的特征,这也是学生易错的地方,并且还容易出现漏解的情况.
【变式3-2】如图.在图中,
(1)同位角共__对,内错角共__对,同旁内角共__对;
(2)与是____,它们是_____被___截成的;
(3)与中_____被_____所截而得到的角;
(4)和被所截而成的内错角是_______,同旁内角是_______.
【答案】 内错角 和 和 和 和
【分析】(1)直接利用同位角、内错角、同旁内角的定义得出答案;
(2)利用内错角的定义得出答案;
(3)利用内错角的定义得出答案;
(4)利用已知图形得出内错角、同旁内角.
【详解】解:(1)同位角共4对,内错角共6对,同旁内角共12对.
故答案为:4;6;12;
(2)与是内错角,它们是和被截成的.
故答案为:内错角;和;;
(3)与中和被所截而得到的角.
故答案为:和;;
(4)和被所截而成的内错角是和,同旁内角是和.
故答案为:和;和.
【点睛】本题考查了同位角、内错角、同旁内角,解本题的关键在熟练掌握同位角、内错角、同旁内角的定义,并充分利用数形结合思想解答.
【变式3-3】与是直线______ 、______ 被直线______ 所截得的______ ;(填序号)
(①,②,③,④,⑤,⑥同位角,⑦内错角,⑧同旁内角)
【答案】③ ④ ⑤ ⑦
【分析】根据内错角的概念求解即可.
【详解】与是直线、被直线所截得的内错角.
故答案为:③,④,⑤,⑦.
【点睛】本题考查了“三线八角”,熟练掌握同位角、内错角、同旁内角的图形特征是解题的关键.
【考点四 平行线】
【典例4-1】数学活动课上,小亮把两个含30°角的三角板按照如图所示方式摆放,点,,,在同一条直线上,他让小明判断直线与的位置关系,小明很快说出了答案并讲出了判断的依据.请你猜猜小明的答案和理由.
【答案】,理由:内错角相等,两直线平行
【分析】根据三角尺的摆放方式,比较容易找到一组相等的内错角,从而证明两条直线平行.
【详解】,理由:内错角相等,两直线平行
【点睛】本题考查了平行线的判定方法,熟练掌握平行线的判定定理是解题的关键.
【典例4-2】作图题:如图,在平面内有不共线的3个点A,B,C.
(1)作射线BA,在BA延长线上取一点E,使AE=AB;
(2)作线段BC并延长BC到点F,使CF=BC;
(3)连接AC,EF;
(4)度量线段AC和EF的长度,直接写出二者之间的数量关系_______,观察AC和FE的位置是 (填“平行”或“相交”)关系;
(5)作BC的中点D,连接AD,猜想S三角形ABD S三角形ACD(填“>”“=”或“<”).
【答案】(1)见解析;(2)见解析;(3)见解析;(4)AC=EF(或EF=2AC),平行;(5)=
【分析】(1)、(2)、(3)利用射线、线段的定义和几何语言画出对应的几何图形即可;
(4)通过观察测量进行判断;
(5)根据等底同高的两个三角形面积相等进行判断.
【详解】解:(1)(2)(3)如图所示:
(4)通过测量观察,可知AC=EF(或EF=2AC),AC∥EF,
故答案为:AC=EF(或EF=2AC);平行;
(5)∵D为BC的中点,三角形ABD与三角形ACD等底同高,
∴S三角形ABD=S三角形ACD.
故答案为:=.
【点睛】本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).
【典例4-3】在同一平面内,任意三条直线有哪几种不同的位置关系?你能画图说明吗?
下面是小明的解题过程:
解:有两种位置关系,如图:
你认为小明的解答正确吗?如果不正确,请你给出正确的解答.
【答案】不正确,在同一平面内,任意三条直线有四种不同的位置关系.
【分析】结合两条直线的位置关系,仔细读题分析,写出三条直线的位置关系.
【详解】不正确,
如图所示,
故在同一平面内,任意三条直线有四种不同的位置关系.
【点睛】此题重点考查学生对三条直线的位置关系的理解,熟练掌握两条直线的位置关系是解题的关键.
针对训练4
【变式4-1】(1)观察如图所示的长方体后填空
用符号表示下列两棱的位置关系:
A1B1____AB ,AA1____AB ,
A1D1____C1D1 , AD____BC;
(2)A1B1与BC所在的直线是两条不相交的直线,他们_ ___平行线(填“是”或“不是”).由此可知,在__________,两条不相交的直线才能叫平行线.
(3)在同一平面内,两条不重合的直线位置关系只有_____种,即_____________.
【答案】(1)∥,⊥,⊥,∥;(2)不是,同一平面内;(3)2,相交或平行.
【详解】(1)A1B1∥AB ,AA1⊥AB ,
A1D1⊥C1D1 , AD∥BC;
(2)A1B1与BC所在的直线是两条不相交的直线,他们不是平行线(填“是”或“不是”).由此可知,在同一平面内,两条不相交的直线才能叫平行线.
(3)在同一平面内,两条不重合的直线位置关系只有2种,即相交和平行.
【变式4-2】5.下列三种说法:
①相等的角是对顶角.
②若线段AB与线段CD没有交点,则ABCD.
③若a、b、c都是直线,且ab,bc,则a与c不相交.
正确的是 _____.
【答案】③
【分析】根据两点间的距离、对顶角、线段和平行线的知识,对选项一一分析,即可求解.
【详解】解:①相等的角不一定是对顶角,故①说法错误;
②在同一平面内,若直线AB与CD没有交点,则ABCD,故②说法错误;
③若直线ab,bc,则ac,a与c不相交,符合平行公理,故③正确.
故答案为:③.
【点睛】本题考查了两点间的距离、对顶角、线段和平行线的知识,掌握以上知识是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
数学七年级下暑假培优专题训练
专题一、相交线、平行线
【专题导航】
目录
【考点一 对顶角邻补角的判断】............................................1
【考点二 垂线的性质】....................................................5
【考点三 三线八角】.....................................................7
【考点四 平行线】.......................................................10
【聚焦考点1】
知识点一、相交线
直线的位置关系:在同一平面内,不重合的两条直线之间的位置关系只有两种:相交或平行。
1.对顶角的概念:①两个角有公共顶点;②两个角的边互为反向延长线
2.邻补角的概念 ①两个角有公共顶点; ② 有一条公共边;③另一边互为反向延长线
3.对顶角的性质:对顶角相等
4.邻补角的性质:邻补角互补
【典例剖析1】
【考点一 对顶角邻补角的判断】
【典例1-1】当光线从空气中射入某种液体中时,光线的传播方向发生了变化,在物理学中这种现象叫做光的折射.如图,液面MN于点D,一束光线沿CD射入液面,在点D处发生折射,折射光线为DE,点F为CD的延长线上一点,若入射角,折射角,则的度数为( )
A.14° B.16° C.18° D.25°
【典例1-2】如图,是一座正八边形古塔,某数学兴趣小组的同学想知道这个正八边形古塔的一个内角的度数,在不能进入塔内测量的情况下,设计了如图所示的测量方案:①反向延长正八边形内角∠AOB的两边,得到∠COD;②测量∠COD的度数.则∠COD的度数即为正八边形古塔内角∠AOB的度数.其中的数学原理是( )
A.邻补角互补 B.对顶角相等 C.同位角相等 D.内错角相等
【典例1-3】(1)如图(1),已知直线a、b相交于点 O,则(1)图中共有几对对顶角 几对邻补角?
(2)如图(2),已知直线a、b、c、d是经过点O的四条直线,则图(2)中共有几对对顶角(不含平角) 几对邻补角?
针对训练1
【变式1-1】如图,直线CD,EF相交于点O,射线OA在∠COF的内部,∠DOF=∠AOD.
(1)如图1,若∠AOC=120°,求∠EOC的度数;
(2)如图2,若∠AOC=α(60°<α<180°),将射线OA绕点O逆时针旋转60°,到OB,
①求∠EOB的度数(用含α的式子表示);
②观察①中的结果,直接写出∠AOC,∠EOB之间的数量关系.
(3)如图3 ,0°<∠AOC <120°,将射线OA绕点O顺时针旋转60°,到OB,请直接写出∠AOC,∠EOB之间的数量关系.
【变式1-2】如图,直线AB、EF相交于点D,∠ADC=90°.
(1)∠2的余角有 ; ,理由是 ;
(2)若∠1与∠2的度数之比为1:3,求∠CDF的度数,请完成填空:
设∠1的度数为,所以∠2= °(用表示),因为∠ADC=90°,所以∠1+∠2= °(用表示)=90°.所以∠1= °,所以∠2= °,所以∠CDF= °.
【变式1-3】如图,直线相交于点O,,平分,.
(1)当时,求的度数(填空完成下列说理过程);
解: (已知)
________
________(邻补角定义)
________
平分(已知)
________ (________)
________
(2)当________时,(直接填空).
【变式1-4】如图,已知DE//BF,AC平分∠BAE,,那么∠ACF的度数是多少?(完成以下说理过程)
解:因为(________),(已知),
所以∠BAE=________(等式性质).
又因为AC平分∠BAE(已知),
所以(_______),
所以(等式性质).
【变式1-5】(1)如图1,点B在直线AC上,∠ABD90°,BE平分∠ABD.试说明∠CBD2∠DBE.
(2)如图2,点B在直线AC上,∠EBD90°,BF平分∠ABD,试说明∠CBD2∠EBF.
(3)如图3,点B在直线AC上,∠EBD90°,BF平分∠ABD,(2)中的结论还成立吗?如果不成立,写出你发现的结论,并说明理由;如果成立,也请说明理由.
【聚焦考点2】
知识点二
1.垂线的概念:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直。垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足,如下图,AB⊥CD,垂足为点O。
2.垂线的基本性质:
① 经过一点有且只有一条直线垂直于已知直线;
② 连接直线外一点与直线上各点的所有线段中,垂线段最短;
③ 从直线外一点到直线的垂线段的长度,叫做点到直线的距离。
3. 垂线的画法
过一点画已知直线的垂线有两种方法:一是用三角板,二是用量角器。有这两种工具时,应掌握“一靠二过三画”这一要领。
【典例剖析2】
【考点二 垂线的性质】
【典例2-1】如图,直线相交于点O,平分,求的度数.
【典例2-2】作图:(使用铅笔作图,保留作图痕迹)
如图,外有一点,画出点到三角形三边的垂线分别交于点、、.
【典例2-3】如图,在直角三角形中,,,.请解答下列问题:
(1)点B到的距离是 ,点A到的距离是 ;
(2)请在图中作出点C到的垂线段;
(3) (填“”、“”、“”),理由是 .
针对训练2
【变式2-1】如图,的三个顶点A、B、C在正方形网格中,每个小方格的边长都为1.请在方格纸上画图并回答下列问题:
(1)过C点画直线的垂线,垂足为点E;
(2)过A点画射线,交直线于点F;
(3)点C到直线的距离为线段___________的长度;
(4)比较大小:线段___________线段(填“>”、“”或“=”).
【变式2-2】如图,直线外有一点,点都在直线上,,已知,,,,则点到直线的距离是_________.
【聚焦考点3】
知识点三、三线八角
如下图,直线AB、CD被直线EF所截,形成的独立的角有八个,简称为“三线八角”。
1.同位角“F”:没有公共顶点的两个角,它们在直线AB,CD的同侧,在第三条直线EF的同旁(即位置相同,如∠1和∠8分别在AB、CD的上方且在EF的右侧),这样的一对角叫做同位角。
2.内错角“Z””/N”:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的两旁(即位置交错,如∠4和∠5都在AB、CD之间,EF的两侧),这样的一对角叫做内错角。
3.同旁内角“U”:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的同旁(如∠3和∠5都在AB、CD之间,EF的两侧),这样的一对角叫做同旁内角。
注:1.这三类角都是成对出现的;
2.这三类角必须是两条直线被第三条直线所截形成的;
3.每对角没有公共的顶点
【典例剖析3】
【考点三 三线八角】
【典例3-1】据说中国最早的风筝是由古代哲学家墨翟制作的.如图风筝的骨架构成了多种位置关系的角.下列角中与∠1构成同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
【典例3-2】如图,在三角形所在平面内画一条直线,使得与成同旁内角的角有3个.若与成同旁内角的角有4个,则该怎样画这条直线?
【典例3-3】如图,在直角三角形中,若斜边为,两直角边分别为,,设,,.
(1)试用所学知识说明:斜边是最长的边;
(2)试用所学知识说明:;
(3)试化简.
针对训练3
【变式3-1】如图所示.
(1)与,与,与各是什么角,是哪两条直线被哪一条直线所截得的?
(2)的内错角有哪些?
(3)写出直线,被所截得的同旁内角,直线,被所截得的同旁内角.
【变式3-2】如图.在图中,
(1)同位角共__对,内错角共__对,同旁内角共__对;
(2)与是____,它们是_____被___截成的;
(3)与中_____被_____所截而得到的角;
(4)和被所截而成的内错角是_______,同旁内角是_______.
【变式3-3】与是直线______ 、______ 被直线______ 所截得的______ ;(填序号)
(①,②,③,④,⑤,⑥同位角,⑦内错角,⑧同旁内角)
【聚焦考点4】
知识点四
平行线
1.平行线的概念:①在同一平面内, ②不相交的两条直线叫做平行线。
平行线用符号“∥”表示,如:直线与直线互相平行,记作∥,读作a平行于b。
2.平行线画法:过直线外一点画已知直线的平行线,可按“一落,二靠,三移,四画”四步操作,如图
3. 平行公理及其推论
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
推论:如果两条直线都与第三条直线平行,那么这两直线也互相平行。简称平行于同一条直线的两条直线也互相平行。用符号语言表示为:∵a∥b, c∥b ∴a∥c
【典例剖析4】
【考点四 平行线】
【典例4-1】数学活动课上,小亮把两个含30°角的三角板按照如图所示方式摆放,点,,,在同一条直线上,他让小明判断直线与的位置关系,小明很快说出了答案并讲出了判断的依据.请你猜猜小明的答案和理由.
【典例4-2】作图题:如图,在平面内有不共线的3个点A,B,C.
(1)作射线BA,在BA延长线上取一点E,使AE=AB;
(2)作线段BC并延长BC到点F,使CF=BC;
(3)连接AC,EF;
(4)度量线段AC和EF的长度,直接写出二者之间的数量关系_______,观察AC和FE的位置是 (填“平行”或“相交”)关系;
(5)作BC的中点D,连接AD,猜想S三角形ABD S三角形ACD(填“>”“=”或“<”).
【典例4-3】在同一平面内,任意三条直线有哪几种不同的位置关系?你能画图说明吗?
下面是小明的解题过程:
解:有两种位置关系,如图:
你认为小明的解答正确吗?如果不正确,请你给出正确的解答.
针对训练4
【变式4-1】(1)观察如图所示的长方体后填空
用符号表示下列两棱的位置关系:
A1B1____AB ,AA1____AB ,
A1D1____C1D1 , AD____BC;
(2)A1B1与BC所在的直线是两条不相交的直线,他们_ ___平行线(填“是”或“不是”).由此可知,在__________,两条不相交的直线才能叫平行线.
(3)在同一平面内,两条不重合的直线位置关系只有_____种,即_____________.
【变式4-2】下列三种说法:
①相等的角是对顶角.
②若线段AB与线段CD没有交点,则ABCD.
③若a、b、c都是直线,且ab,bc,则a与c不相交.
正确的是 _____.
数学七年级下暑假培优专题训练
专题一、相交线(解析版)
【典例剖析】
【考点一 对顶角邻补角的判断】
【典例1-1】当光线从空气中射入某种液体中时,光线的传播方向发生了变化,在物理学中这种现象叫做光的折射.如图,液面MN于点D,一束光线沿CD射入液面,在点D处发生折射,折射光线为DE,点F为CD的延长线上一点,若入射角,折射角,则的度数为( )
A.14° B.16° C.18° D.25°
【答案】A
【分析】根据对顶角相等,计算角的差即可;
【详解】解:∵F点在CD延长线上,
∴∠1=∠FDB=50°,
∴∠EDF=∠FDB-∠2=14°,
故选: A.
【点睛】本题考查了对顶角的概念:有一个公共顶点,且一个角的两条边分别是另一个角的两条边的反向延长线,那么这两个角就叫做对顶角.
【典例1-2】如图,是一座正八边形古塔,某数学兴趣小组的同学想知道这个正八边形古塔的一个内角的度数,在不能进入塔内测量的情况下,设计了如图所示的测量方案:①反向延长正八边形内角∠AOB的两边,得到∠COD;②测量∠COD的度数.则∠COD的度数即为正八边形古塔内角∠AOB的度数.其中的数学原理是( )
A.邻补角互补 B.对顶角相等 C.同位角相等 D.内错角相等
【答案】B
【分析】根据对顶角相等解答即可.
【详解】根据对顶角相等可知:∠AOB=∠COD;
故选:B
【点睛】本题考查的是对顶角,掌握对顶角相等是解题的关键.
【典例1-3】(1)如图(1),已知直线a、b相交于点 O,则(1)图中共有几对对顶角 几对邻补角?
(2)如图(2),已知直线a、b、c、d是经过点O的四条直线,则图(2)中共有几对对顶角(不含平角) 几对邻补角?
【答案】(1)2对对顶角,4对邻补角;(2)图中共有12对对顶角,24对邻补角
【分析】(1)根据对顶角、邻补角的定义判断即可;
(2)先将图(2)拆分成如图的形式,再根据(1)的结论判断即可.
【详解】解:(1)根据题图可知,图中共有2对对顶角,4对邻补角;
(2)将图(2)拆分为下图:
通过观察图形.不难发现a、b、c、d四条直线两两相交,最多有6个交点,而由(1)知:每个交点处有两对对顶角,有四对邻补角,
对顶角的对数:(对);邻补角的对数:(对);
答:图中共有12对对顶角,24对邻补角;
【点睛】本题考查了对顶角、邻补角的定义;仔细观察图形弄清各个角之间的对顶角关系和邻补角关系是解题的关键.
针对训练1
【变式1-1】如图,直线CD,EF相交于点O,射线OA在∠COF的内部,∠DOF=∠AOD.
(1)如图1,若∠AOC=120°,求∠EOC的度数;
(2)如图2,若∠AOC=α(60°<α<180°),将射线OA绕点O逆时针旋转60°,到OB,
①求∠EOB的度数(用含α的式子表示);
②观察①中的结果,直接写出∠AOC,∠EOB之间的数量关系.
(3)如图3 ,0°<∠AOC <120°,将射线OA绕点O顺时针旋转60°,到OB,请直接写出∠AOC,∠EOB之间的数量关系.
【答案】(1)∠EOC=20°;
(2)①∠EOB=;②∠EOB=∠AOC;
(3)当0°<∠AOC ≤90°时,∠EOB=∠AOC+120°;当90°<∠AOC ≤120°时,∠EOB=240°-∠AOC.
【分析】(1)根据补角的定义求出∠AOD,结合已知求出∠DOF,然后根据对顶角相等得出答案;
(2)①根据补角的定义求出∠AOD,结合已知求出∠DOF,然后根据对顶角相等求出∠EOC,再根据∠BOC=α-60°,求出∠EOB的度数即可;②根据题意结合补角的定义求出∠AOD=180°-∠AOC,∠BOC=∠AOC-60°,然后可得∠DOF=∠AOD=60°-∠AOC,再根据对顶角相等计算得出答案;
(3)分情况讨论:①当0°<∠AOC ≤90°时,根据题意结合补角的定义求出∠AOD=180°-∠AOC,∠BOC=∠AOC+60°,然后可得∠DOF=∠AOD=60°-∠AOC,再根据对顶角相等计算得出答案;②当90°<∠AOC ≤120°时,根据题意结合补角的定义求出∠AOD=180°-∠AOC,∠BOC=∠AOC+60°,然后可得∠DOF=∠AOD=60°-∠AOC,再根据对顶角相等计算得出∠EOC+∠BOC=∠AOC+120°,最后根据周角的定义计算得出答案.
【详解】(1)解:∵∠AOC=120°,
∴∠AOD=180°-∠AOC=180°-120°=60°,
∴∠DOF=∠AOD=20°,
∴∠EOC=∠DOF=20°;
(2)解:①∵∠AOC=α,
∴∠AOD=180°-α,
∴∠DOF=∠AOD=60°-,
∴∠EOC=∠DOF=60°-,
由题意得:∠AOB=60°,
∴∠BOC=α-60°,
∴∠EOB=∠EOC+∠BOC=60°-+α-60°=;
②观察①中结果可得:∠EOB=,
证明:∵∠AOD=180°-∠AOC,∠BOC=∠AOC-∠AOB=∠AOC-60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOB=∠EOC+∠BOC=60°-∠AOC+∠AOC-60°=∠AOC;
(3)解:①当0°<∠AOC ≤90°时,
如图,∵∠AOD=180°-∠AOC,∠BOC=∠AOC+∠AOB=∠AOC+60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOB=∠EOC+∠BOC=60°-∠AOC+∠AOC+60°=∠AOC+120°.
②当90°<∠AOC ≤120°时,
如图,∵∠AOD=180°-∠AOC,∠BOC=∠AOC+∠AOB=∠AOC+60°,
∴∠DOF=∠AOD=60°-∠AOC,
∴∠EOC=∠DOF=60°-∠AOC,
∴∠EOC+∠BOC=60°-∠AOC+∠AOC+60°=∠AOC+120°,
∴∠EOB=360°-(∠EOC+∠BOC)=360°-∠AOC-120°=240°-∠AOC.
【点睛】本题考查了补角的定义,角的和差计算,对顶角相等,理清各角之间的关系是正确计算的前提.
【变式1-2】如图,直线AB、EF相交于点D,∠ADC=90°.
(1)∠2的余角有 ; ,理由是 ;
(2)若∠1与∠2的度数之比为1:3,求∠CDF的度数,请完成填空:
设∠1的度数为,所以∠2= °(用表示),因为∠ADC=90°,所以∠1+∠2= °(用表示)=90°.所以∠1= --°,所以∠2=---- °,所以∠CDF= -----°.
【答案】(1)∠1和∠BDF;∠BDF,同角的余角相等 ;(2)3x °,4x °,22.5 °,67.5 °,112.5 °.
【分析】(1)根据对顶角的定义以及余角的定义填空;
(2)根据题意,补充完整解题过程即可.
【详解】解:如图,因为直线AB、EF相交于点D,∠ADC=90°,
(1)∠2的余角有∠1和∠BDF;∠BDF,理由是 同角的余角相等 ;
(2)设∠1的度数为,所以∠2= 3x °(用表示),
因为∠ADC=90°,
所以∠1+∠2= 4x °(用表示)=90°.
所以∠1= 22.5 °,所以∠2= 67.5 °,
所以∠CDF= 112.5 °.
【点睛】本题考查了对顶角的定义,余角和补角,熟记概念并准确识图是解题的关键.
【变式1-3】如图,直线相交于点O,,平分,.
(1)当时,求的度数(填空完成下列说理过程);
解: (已知)
________
________(邻补角定义)
________
平分(已知)
________ (________)
________
(2)当________时,(直接填空).
【答案】(1),,,,角平分线定义,
(2)
【分析】(1)先根据平角的定义求出,再根据邻补角的定义求出,即可根据角平分线的定义求出的度数;
(2)同(1)推理过程求出,,再由,建立方程求解即可.
【详解】(1)解: (已知)
,
(邻补角定义)
,
平分(已知)
(角平分线的定义)
,
故答案为:,,,,角平分线定义,;
(2)解:,,
,
,
平分(已知)
,
∵,
∴,
解得
∴当时,,
故答案为:.
【点睛】本题主要考查了几何图形中角度的计算,角平分线的定义,灵活运用所学知识是解题的关键.
【变式1-4】如图,已知DE//BF,AC平分∠BAE,,那么∠ACF的度数是多少?(完成以下说理过程)
解:因为(________),(已知),
所以∠BAE=________(等式性质).
又因为AC平分∠BAE(已知),
所以(_______),
所以(等式性质).
【答案】邻补角的定义;110°;角平分线的定义.
【分析】根据邻补角的定义可得∠BAE=110°,由角平分线的定义得出∠CAE=BAE,即可得出结果.
【详解】解:因为∠BAD+∠BAE=180°(邻补角的定义),∠BAD=70°(已知),
所以∠BAE=110°(等式性质),
又因为AC平分∠BAE(已知),
所以∠CAE=BAE(角平分线的定义),
所以∠CAE=55°(等式性质).
故答案为:邻补角的定义;110°;角平分线的定义.
【点睛】题目主要考查邻补角的定义及角平分线的定义,理解这两个定义是解题关键.
【变式1-5】(1)如图1,点B在直线AC上,∠ABD90°,BE平分∠ABD.试说明∠CBD2∠DBE.
(2)如图2,点B在直线AC上,∠EBD90°,BF平分∠ABD,试说明∠CBD2∠EBF.
(3)如图3,点B在直线AC上,∠EBD90°,BF平分∠ABD,(2)中的结论还成立吗?如果不成立,写出你发现的结论,并说明理由;如果成立,也请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)成立,理由见解析
【分析】(1)分别求解 从而可得结论;
(2)先证明可得再利用等量代换可得结论;
(3)设 求解 再求解 从而可得结论.
【详解】解:(1) 点B在直线AC上,∠ABD90°,
BE平分∠ABD,
(2) 点B在直线AC上,∠EBD90°,
BF平分∠ABD,
即
(3)成立,理由见解析:
设 而BF平分∠ABD,
∠EBD90°,
【点睛】本题考查的是与余角和补角有关的计算,角平分线的定义,熟练的运用角的和差运算是解本题的关键.
【考点二 垂线的性质】
【典例2-1】如图,直线相交于点O,平分,求的度数.
【答案】
【分析】先根据垂直的定义得到,则,根据角平分线的定义得到,则由平角的定义可得.
【详解】解:∵,
∴,
∵,
∴,
∵平分,
∴,
∴.
【点睛】本题主要考查了几何图形中角度的计算,垂直的定义,角平分线的定义,灵活运用所学知识是解题的关键.
【典例2-2】作图:(使用铅笔作图,保留作图痕迹)
如图,外有一点,画出点到三角形三边的垂线分别交于点、、.
【答案】见解析
【分析】根据题意,过点分别作的垂线,垂足分别为,
【详解】解:如图所示,过点分别作的垂线,垂足分别为,则即为所求
【点睛】本题考查了作垂线,熟练掌握基本作图是解题的关键.
【典例2-3】如图,在直角三角形中,,,.请解答下列问题:
(1)点B到的距离是 ,点A到的距离是 ;
(2)请在图中作出点C到的垂线段;
(3) (填“”、“”、“”),理由是 .
【答案】(1)8,6
(2)见解析
(3)
【分析】(1)根据点到直线的距离的定义求解;
(2)过点作的垂线,垂足为;
(3)根据垂线段最短进行判断.
【详解】(1)解:点B到的距离是,点A到的距离是;
故答案为:8,6;
(2)如图,为所作;
(3),理由是垂线段最短.
故答案为:;垂线段最短.
【点睛】本题考查了点到直线的距离,垂线段最短,熟练掌握点到直线距离的概念是解答本题的关键.直线外一点到这条直线的垂线段的长度,叫做这个点到这条直线的距离.
针对训练2
【变式2-1】如图,的三个顶点A、B、C在正方形网格中,每个小方格的边长都为1.请在方格纸上画图并回答下列问题:
(1)过C点画直线的垂线,垂足为点E;
(2)过A点画射线,交直线于点F;
(3)点C到直线的距离为线段___________的长度;
(4)比较大小:线段___________线段(填“>”、“”或“=”).
【答案】(1)见解析
(2)见解析
(3)
(4)
【分析】(1)根据网格的特点作图即可;
(2)根据网格的特点作图即可;
(3)根据点到直线的距离的概念解答;
(4)根据垂线段最短解答.
【详解】(1)如图,直线即为所作;
(2)如图,射线即为所作;
(3)点C到直线的距离为线段的长度;
故答案为:;
(4)根据垂线段最短得:线段线段;
故答案为:.
【点睛】本题考查了利用网格作图、垂线段最短以及点到直线的距离等知识,熟练掌握相关知识是解题的关键.
【变式2-2】如图,直线外有一点,点都在直线上,,已知,,,,则点到直线的距离是_________.
【答案】4
【分析】直线外一点到直线的垂线段的长度,叫做点到直线的距离,由此即可得到答案.
【详解】解:直线外一点到直线的垂线段的长度,叫做点到直线的距离,,
点到直线的距离是4,
故答案为:4.
【点睛】本题考查点到直线的距离,关键是掌握点到直线的距离的定义.
【考点三 三线八角】
【典例3-1】据说中国最早的风筝是由古代哲学家墨翟制作的.如图风筝的骨架构成了多种位置关系的角.下列角中与∠1构成同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
【答案】A
【分析】根据同位角的定义解答.两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【详解】解:由图可得,与构成同位角的是.
故选:A.
【点睛】本题主要考查了同位角的定义,解题的关键是明确同位角的边构成“”形,内错角的边构成“”形,同旁内角的边构成“”形.
【典例3-2】如图,在三角形所在平面内画一条直线,使得与成同旁内角的角有3个.若与成同旁内角的角有4个,则该怎样画这条直线?
【答案】见解析
【分析】根据同旁内角的定义进行画图即可:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
【详解】解:如图1所示,与成同旁内角的角有共3个;
如图2所示,与成同旁内角的角有共4个.
【点睛】本题主要考查了同旁内角的定义,熟知相关定义是解题的关键.
【典例3-3】如图,在直角三角形中,若斜边为,两直角边分别为,,设,,.
(1)试用所学知识说明:斜边是最长的边;
(2)试用所学知识说明:;
(3)试化简.
【答案】(1),,中,斜边最长
(2)
(3)
【分析】(1)利用垂线段最短即可确定出,,的长短关系,问题即可解答;
(2)由两点之间,线段最短,即可得到结论成立;
(3)由三角形三边关系可以得到,结合(1)即可去掉绝对值号,然后合并同类项解答题目.
【详解】(1)解:因为是点C到直线AB的垂线段,
所以.
因为AB是点B到直线AC的垂线段,所以,
故,,中,斜边最长.
(2)解:因为点C与点B之间,BC是线段,而是折线,根据“两点之间,线段最短”,可得,即.
(3)解:∵,,,
∴,,,
∴原式.
【点睛】本题考查垂线段最短,两点间线段最短及绝对值化简问题,侧重考查知识点的记忆、理解、应用能力,解题的关键是掌握垂线段最短及两点间线段最短.
针对训练3
【变式3-1】如图所示.
(1)与,与,与各是什么角,是哪两条直线被哪一条直线所截得的?
(2)的内错角有哪些?
(3)写出直线,被所截得的同旁内角,直线,被所截得的同旁内角.
【答案】(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据同位角概念解答即可;
(2)根据内错的概念解答即可;
(3)根据同旁内角的概念解答即可.
【详解】(1)解:与是直线、被直线所截形成的同位角,
与是直线、被直线所截形成的同位角,
与是直线、被直线所截形成的同位角;
(2)解:当直线与被所截时,与是内错角,
当直线和被所截时,与是内错角;
(3)解:直线,被所截得的同旁内角有与,
直线,被所截得的同旁内角与.
【点睛】本题考查了同位角、内错角、同旁内角,解本题的关键要抓住各类角的特征,这也是学生易错的地方,并且还容易出现漏解的情况.
【变式3-2】如图.在图中,
(1)同位角共__对,内错角共__对,同旁内角共__对;
(2)与是____,它们是_____被___截成的;
(3)与中_____被_____所截而得到的角;
(4)和被所截而成的内错角是_______,同旁内角是_______.
【答案】 内错角 和 和 和 和
【分析】(1)直接利用同位角、内错角、同旁内角的定义得出答案;
(2)利用内错角的定义得出答案;
(3)利用内错角的定义得出答案;
(4)利用已知图形得出内错角、同旁内角.
【详解】解:(1)同位角共4对,内错角共6对,同旁内角共12对.
故答案为:4;6;12;
(2)与是内错角,它们是和被截成的.
故答案为:内错角;和;;
(3)与中和被所截而得到的角.
故答案为:和;;
(4)和被所截而成的内错角是和,同旁内角是和.
故答案为:和;和.
【点睛】本题考查了同位角、内错角、同旁内角,解本题的关键在熟练掌握同位角、内错角、同旁内角的定义,并充分利用数形结合思想解答.
【变式3-3】与是直线______ 、______ 被直线______ 所截得的______ ;(填序号)
(①,②,③,④,⑤,⑥同位角,⑦内错角,⑧同旁内角)
【答案】③ ④ ⑤ ⑦
【分析】根据内错角的概念求解即可.
【详解】与是直线、被直线所截得的内错角.
故答案为:③,④,⑤,⑦.
【点睛】本题考查了“三线八角”,熟练掌握同位角、内错角、同旁内角的图形特征是解题的关键.
【考点四 平行线】
【典例4-1】数学活动课上,小亮把两个含30°角的三角板按照如图所示方式摆放,点,,,在同一条直线上,他让小明判断直线与的位置关系,小明很快说出了答案并讲出了判断的依据.请你猜猜小明的答案和理由.
【答案】,理由:内错角相等,两直线平行
【分析】根据三角尺的摆放方式,比较容易找到一组相等的内错角,从而证明两条直线平行.
【详解】,理由:内错角相等,两直线平行
【点睛】本题考查了平行线的判定方法,熟练掌握平行线的判定定理是解题的关键.
【典例4-2】作图题:如图,在平面内有不共线的3个点A,B,C.
(1)作射线BA,在BA延长线上取一点E,使AE=AB;
(2)作线段BC并延长BC到点F,使CF=BC;
(3)连接AC,EF;
(4)度量线段AC和EF的长度,直接写出二者之间的数量关系_______,观察AC和FE的位置是 (填“平行”或“相交”)关系;
(5)作BC的中点D,连接AD,猜想S三角形ABD S三角形ACD(填“>”“=”或“<”).
【答案】(1)见解析;(2)见解析;(3)见解析;(4)AC=EF(或EF=2AC),平行;(5)=
【分析】(1)、(2)、(3)利用射线、线段的定义和几何语言画出对应的几何图形即可;
(4)通过观察测量进行判断;
(5)根据等底同高的两个三角形面积相等进行判断.
【详解】解:(1)(2)(3)如图所示:
(4)通过测量观察,可知AC=EF(或EF=2AC),AC∥EF,
故答案为:AC=EF(或EF=2AC);平行;
(5)∵D为BC的中点,三角形ABD与三角形ACD等底同高,
∴S三角形ABD=S三角形ACD.
故答案为:=.
【点睛】本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).
【典例4-3】在同一平面内,任意三条直线有哪几种不同的位置关系?你能画图说明吗?
下面是小明的解题过程:
解:有两种位置关系,如图:
你认为小明的解答正确吗?如果不正确,请你给出正确的解答.
【答案】不正确,在同一平面内,任意三条直线有四种不同的位置关系.
【分析】结合两条直线的位置关系,仔细读题分析,写出三条直线的位置关系.
【详解】不正确,
如图所示,
故在同一平面内,任意三条直线有四种不同的位置关系.
【点睛】此题重点考查学生对三条直线的位置关系的理解,熟练掌握两条直线的位置关系是解题的关键.
针对训练4
【变式4-1】(1)观察如图所示的长方体后填空
用符号表示下列两棱的位置关系:
A1B1____AB ,AA1____AB ,
A1D1____C1D1 , AD____BC;
(2)A1B1与BC所在的直线是两条不相交的直线,他们_ ___平行线(填“是”或“不是”).由此可知,在__________,两条不相交的直线才能叫平行线.
(3)在同一平面内,两条不重合的直线位置关系只有_____种,即_____________.
【答案】(1)∥,⊥,⊥,∥;(2)不是,同一平面内;(3)2,相交或平行.
【详解】(1)A1B1∥AB ,AA1⊥AB ,
A1D1⊥C1D1 , AD∥BC;
(2)A1B1与BC所在的直线是两条不相交的直线,他们不是平行线(填“是”或“不是”).由此可知,在同一平面内,两条不相交的直线才能叫平行线.
(3)在同一平面内,两条不重合的直线位置关系只有2种,即相交和平行.
【变式4-2】5.下列三种说法:
①相等的角是对顶角.
②若线段AB与线段CD没有交点,则ABCD.
③若a、b、c都是直线,且ab,bc,则a与c不相交.
正确的是 _____.
【答案】③
【分析】根据两点间的距离、对顶角、线段和平行线的知识,对选项一一分析,即可求解.
【详解】解:①相等的角不一定是对顶角,故①说法错误;
②在同一平面内,若直线AB与CD没有交点,则ABCD,故②说法错误;
③若直线ab,bc,则ac,a与c不相交,符合平行公理,故③正确.
故答案为:③.
【点睛】本题考查了两点间的距离、对顶角、线段和平行线的知识,掌握以上知识是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
