河北省邢台市信都区2022-2023学年七年级下学期5月月考数学试题(含答案)
文档属性
| 名称 | 河北省邢台市信都区2022-2023学年七年级下学期5月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 439.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-26 16:07:40 | ||
图片预览


文档简介
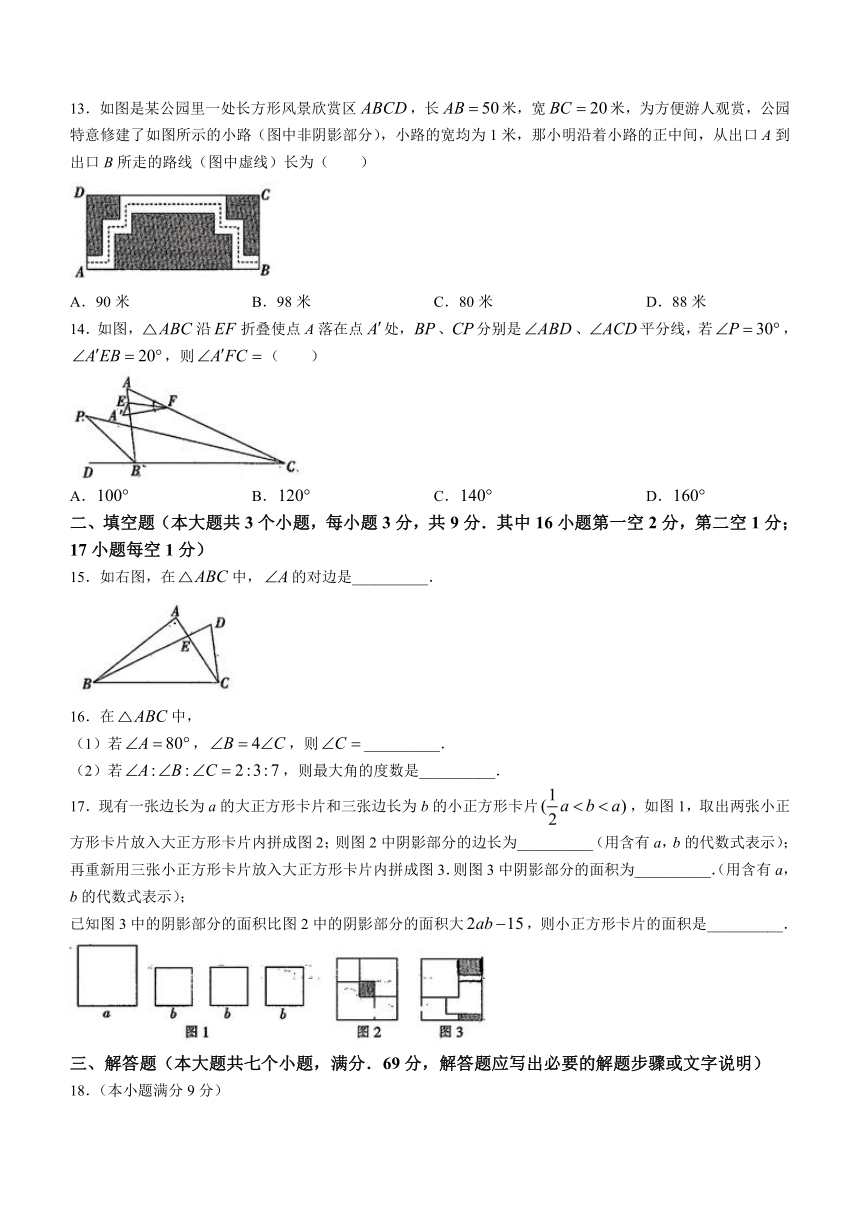
2022-2023学年第二学期阶段练习二
七年级数学试题(冀教版)
考试范围:6-10章
说明:1.本试卷共6页,满分120分。
2.请将所有答案填涂在答题卡上,答在本试卷上无效。
一、选择题(本大题共14个小题,每小题3分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列几何图形是钝角三角形的是( )
A. B. C. D.
2.若是不等式,则符号“●”可以是( )
A. B. C. D.
3.如图,在中,可以说明比大的理由是( )
A.垂线段最短
B.两点可以确定一条直线
C.经过一点有且只有一条直线与已知直线垂直
D.两点之间线段最短
4.若,且,则m的值可以是( )
A.1 B.2 C.3 D.4
5.如图,将折叠,使点C落在边上处,展开后得到折痕l,则l是的( )
A.高 B.中线 C.角平分线 D.无法判断
6.如图,在数轴上表示的x的取值范围是( )
A. B. C. D.
7.如图,平面上直线a,b分别过线段两端点(数据如图),则a,b相交所成的锐角是( )
A. B. C. D.
8.语句“x的与x的差不超过3”可以表示为( )
A. B. C. D.
9.若右图表示三角形分类,则下列说法正确的是( )
A.M表示等边三角形
B.M表示锐角三角形
C.P表示等腰三角形
D.N表示不等边三角形
10.已知1亩药材平均每年可获得收入2万元,某县种植该品种药材8千亩,若用科学记数法表示该县种植此品种药材的年收入是元,则下列说法正确的是( )
A. B. C. D.
11.某商场促销,小明将促销信息告诉了妈妈,现假设某种商品的定价为x元,小明妈妈根据信息列出了不等式,那么小明告诉妈妈的促销信息是( )、
A.买两件该商品先减150元,再打八折,最后付款不超过1500元
B.买两件该商品先打八折,再减150元,最后付款不超过1500元
C.买两件该商品先减150元,再打八折,最后付款不到1500元
D.买两件该商品先打八折,再减150元,最后付款不到1500元
12.老师设计了接力游戏,用合作的方式完成解一元一次不等式,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A.只有乙 B.甲和乙 C.乙和丙 D.乙和丁
13.如图是某公园里一处长方形风景欣赏区,长米,宽米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的正中间,从出口A到出口B所走的路线(图中虚线)长为( )
A.90米 B.98米 C.80米 D.88米
14.如图,沿折叠使点A落在点处,、分别是、平分线,若,,则( )
A. B. C. D.
二、填空题(本大题共3个小题,每小题3分,共9分.其中16小题第一空2分,第二空1分;17小题每空1分)
15.如右图,在中,的对边是__________.
16.在中,
(1)若,,则__________.
(2)若,则最大角的度数是__________.
17.现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片,如图1,取出两张小正方形卡片放入大正方形卡片内拼成图2;则图2中阴影部分的边长为__________(用含有a,b的代数式表示);再重新用三张小正方形卡片放入大正方形卡片内拼成图3.则图3中阴影部分的面积为__________.(用含有a,b的代数式表示);
已知图3中的阴影部分的面积比图2中的阴影部分的面积大,则小正方形卡片的面积是__________.
三、解答题(本大题共七个小题,满分.69分,解答题应写出必要的解题步骤或文字说明)
18.(本小题满分9分)
已知在中,,,且为奇数.
(1)求的周长;
(2)判断的形状.
19.(本小题满分9分)
利用整式乘法公式进行计算
(1);(2).
20.(本小题满分9分)
已知.
(1)用含有x的式子表示y;
(2)若y满足,求x的取值范围.
21.(本小题满分10分)
如图,课本上利用实验剪拼的方法,把和移动到的右侧,且使这三个角的顶点重合,再利用平行线的性质可以说明三角形内角和定理。
具体说理过程如下:
延长,过点C作.
___________(两直线平行,内错角相等),
(___________,(____________)
(平角定义),
.(____________)
(1)请你补充完善上述说理过程;
(2)请你参考实验1的解题思路,自行画图标注好顶点字母,写出实验2说明三角形内角和定理的过程.
22.(本小题满分10分)
嘉淇准备完成题目:解不等式组时,发现常数“□”印刷不清楚.
(1)他把“□”猜成,请你解不等式组;
(2)王老师说:“不等式组的解集是,请求常数“□”的取值范围.
23.(本小题满分10分)
如图,中,于点D,,平分交于E,.
(1)求的度数;
(2)若点F为线段上的任意一点,当为直角三角形时,求的度数.
24.(本小题满分12分)
某社区原来每天需要处理生活垃圾920吨,刚好被12个A型转运站和10个B型转运站处理完.已知一个A型转运站比一个B型转运站每天多处理7吨生活垃圾.
(1)求一个A型和一个B型转运站每天处理生活垃圾各是多少吨?
(2)由于垃圾分类要求的提高,A型与B型转运站每个每天均少处理8吨生活垃圾,同时由于市民环保意识增强,该社区每天需要处理的生活垃圾比原来少10吨.若该社区计划增设A型、B型转运站共5个,试问至少需要增设几个A型转运站才能当日处理完所有生活垃圾?
2022-2023学年第二学期阶段练习二
七年级数学参考答案(冀教版)
1-5 BDDAA 6-10ABBCC 11-14CBDC
15.BC
16.(1)20 (2)105
17.,,5
18.解:(1)由题意得:,即:,……………………………3分
为奇数,,
的周长为;…………………………………………………………6分
(2),
是等腰三角形…………………………………………………………9分
19.解:(1);…………………………4分
(2)……………………………5分
20.解:(1),
,
;………………………………………………………………4分
(2)根据题意得,解得.…………………………………5分
21.解:(1),两直线平行,同位角相等,等量代换…………………………………3分
(2)如图所示,过点A作直线,
,,
(平角定义),
……………………………………10分
22.解:(1)解不等式,得
解不等式,得
所以不等式组的解集是…………………………………………5分
(2)设常数“ ”为a,
解不等式,得
又因为不等式的解集为,不等式组的解集为
所以,解得, …………………………………………………10分
23.(1)理由如下:,,
,,
,,,
,平分,,
,;……………………6分
(2)解:分两种情况:
①当时,如图1所示:则,
;…………………………………………8分
②当时,如图2所示:
则,;
综上所述:的度数为或.……………………………………………10分
24.解:(1)设每个A型转运站每天处理生活垃圾x吨,每个B型转运站每天处理生活垃圾y吨,
依题意得: ,
解得: .
答:每个A型转运站每天处理生活垃圾45吨,每个B型转运站每天处理生活垃圾
38吨.…………………………………………………………………………6分
(2)设需要增设m个A型转运站,则增设个B型转运站,
依题意得:,
解得: .又为整数,的最小值为3.
答:至少需要增设3个A型转运站才能当日处理完所有生活垃圾.……12分
七年级数学试题(冀教版)
考试范围:6-10章
说明:1.本试卷共6页,满分120分。
2.请将所有答案填涂在答题卡上,答在本试卷上无效。
一、选择题(本大题共14个小题,每小题3分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列几何图形是钝角三角形的是( )
A. B. C. D.
2.若是不等式,则符号“●”可以是( )
A. B. C. D.
3.如图,在中,可以说明比大的理由是( )
A.垂线段最短
B.两点可以确定一条直线
C.经过一点有且只有一条直线与已知直线垂直
D.两点之间线段最短
4.若,且,则m的值可以是( )
A.1 B.2 C.3 D.4
5.如图,将折叠,使点C落在边上处,展开后得到折痕l,则l是的( )
A.高 B.中线 C.角平分线 D.无法判断
6.如图,在数轴上表示的x的取值范围是( )
A. B. C. D.
7.如图,平面上直线a,b分别过线段两端点(数据如图),则a,b相交所成的锐角是( )
A. B. C. D.
8.语句“x的与x的差不超过3”可以表示为( )
A. B. C. D.
9.若右图表示三角形分类,则下列说法正确的是( )
A.M表示等边三角形
B.M表示锐角三角形
C.P表示等腰三角形
D.N表示不等边三角形
10.已知1亩药材平均每年可获得收入2万元,某县种植该品种药材8千亩,若用科学记数法表示该县种植此品种药材的年收入是元,则下列说法正确的是( )
A. B. C. D.
11.某商场促销,小明将促销信息告诉了妈妈,现假设某种商品的定价为x元,小明妈妈根据信息列出了不等式,那么小明告诉妈妈的促销信息是( )、
A.买两件该商品先减150元,再打八折,最后付款不超过1500元
B.买两件该商品先打八折,再减150元,最后付款不超过1500元
C.买两件该商品先减150元,再打八折,最后付款不到1500元
D.买两件该商品先打八折,再减150元,最后付款不到1500元
12.老师设计了接力游戏,用合作的方式完成解一元一次不等式,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A.只有乙 B.甲和乙 C.乙和丙 D.乙和丁
13.如图是某公园里一处长方形风景欣赏区,长米,宽米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的正中间,从出口A到出口B所走的路线(图中虚线)长为( )
A.90米 B.98米 C.80米 D.88米
14.如图,沿折叠使点A落在点处,、分别是、平分线,若,,则( )
A. B. C. D.
二、填空题(本大题共3个小题,每小题3分,共9分.其中16小题第一空2分,第二空1分;17小题每空1分)
15.如右图,在中,的对边是__________.
16.在中,
(1)若,,则__________.
(2)若,则最大角的度数是__________.
17.现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片,如图1,取出两张小正方形卡片放入大正方形卡片内拼成图2;则图2中阴影部分的边长为__________(用含有a,b的代数式表示);再重新用三张小正方形卡片放入大正方形卡片内拼成图3.则图3中阴影部分的面积为__________.(用含有a,b的代数式表示);
已知图3中的阴影部分的面积比图2中的阴影部分的面积大,则小正方形卡片的面积是__________.
三、解答题(本大题共七个小题,满分.69分,解答题应写出必要的解题步骤或文字说明)
18.(本小题满分9分)
已知在中,,,且为奇数.
(1)求的周长;
(2)判断的形状.
19.(本小题满分9分)
利用整式乘法公式进行计算
(1);(2).
20.(本小题满分9分)
已知.
(1)用含有x的式子表示y;
(2)若y满足,求x的取值范围.
21.(本小题满分10分)
如图,课本上利用实验剪拼的方法,把和移动到的右侧,且使这三个角的顶点重合,再利用平行线的性质可以说明三角形内角和定理。
具体说理过程如下:
延长,过点C作.
___________(两直线平行,内错角相等),
(___________,(____________)
(平角定义),
.(____________)
(1)请你补充完善上述说理过程;
(2)请你参考实验1的解题思路,自行画图标注好顶点字母,写出实验2说明三角形内角和定理的过程.
22.(本小题满分10分)
嘉淇准备完成题目:解不等式组时,发现常数“□”印刷不清楚.
(1)他把“□”猜成,请你解不等式组;
(2)王老师说:“不等式组的解集是,请求常数“□”的取值范围.
23.(本小题满分10分)
如图,中,于点D,,平分交于E,.
(1)求的度数;
(2)若点F为线段上的任意一点,当为直角三角形时,求的度数.
24.(本小题满分12分)
某社区原来每天需要处理生活垃圾920吨,刚好被12个A型转运站和10个B型转运站处理完.已知一个A型转运站比一个B型转运站每天多处理7吨生活垃圾.
(1)求一个A型和一个B型转运站每天处理生活垃圾各是多少吨?
(2)由于垃圾分类要求的提高,A型与B型转运站每个每天均少处理8吨生活垃圾,同时由于市民环保意识增强,该社区每天需要处理的生活垃圾比原来少10吨.若该社区计划增设A型、B型转运站共5个,试问至少需要增设几个A型转运站才能当日处理完所有生活垃圾?
2022-2023学年第二学期阶段练习二
七年级数学参考答案(冀教版)
1-5 BDDAA 6-10ABBCC 11-14CBDC
15.BC
16.(1)20 (2)105
17.,,5
18.解:(1)由题意得:,即:,……………………………3分
为奇数,,
的周长为;…………………………………………………………6分
(2),
是等腰三角形…………………………………………………………9分
19.解:(1);…………………………4分
(2)……………………………5分
20.解:(1),
,
;………………………………………………………………4分
(2)根据题意得,解得.…………………………………5分
21.解:(1),两直线平行,同位角相等,等量代换…………………………………3分
(2)如图所示,过点A作直线,
,,
(平角定义),
……………………………………10分
22.解:(1)解不等式,得
解不等式,得
所以不等式组的解集是…………………………………………5分
(2)设常数“ ”为a,
解不等式,得
又因为不等式的解集为,不等式组的解集为
所以,解得, …………………………………………………10分
23.(1)理由如下:,,
,,
,,,
,平分,,
,;……………………6分
(2)解:分两种情况:
①当时,如图1所示:则,
;…………………………………………8分
②当时,如图2所示:
则,;
综上所述:的度数为或.……………………………………………10分
24.解:(1)设每个A型转运站每天处理生活垃圾x吨,每个B型转运站每天处理生活垃圾y吨,
依题意得: ,
解得: .
答:每个A型转运站每天处理生活垃圾45吨,每个B型转运站每天处理生活垃圾
38吨.…………………………………………………………………………6分
(2)设需要增设m个A型转运站,则增设个B型转运站,
依题意得:,
解得: .又为整数,的最小值为3.
答:至少需要增设3个A型转运站才能当日处理完所有生活垃圾.……12分
同课章节目录
