函数的概念和图象(江苏省南京市鼓楼区)
图片预览





文档简介
课件13张PPT。2.1 函数的概念和图象在初中, 我们把函数看成是刻画和描述
两个变量之间依赖关系的数学模型. 设在某变化过程中有两个变量x,y。如果
对于x在某一范围内的每一个确定的值,y都有
唯一确定的值与它对应,那么就说y是x的函数,
x叫做自变量。在现实生活中,我们可能会遇到下列问题:(1)我国人口随年份的变化而变化,如:你根据这个表说出在这几年中我国人口的变化情吗?这是通过1969—1999年我国人口数据表来体现
人口随年份的变化而变化在现实生活中,我们可能会遇到下列问题:(2)一物体从静止开始下落,下落的距离y(m)与
下落时间x(s)之间近似地满足关系式y=4.9x2.若一物体下落2s,你能求出它下落的距离吗?这是通过代数表达式来体现:
距离随时间的变化而变化在现实生活中,有时我们还用图象来表达
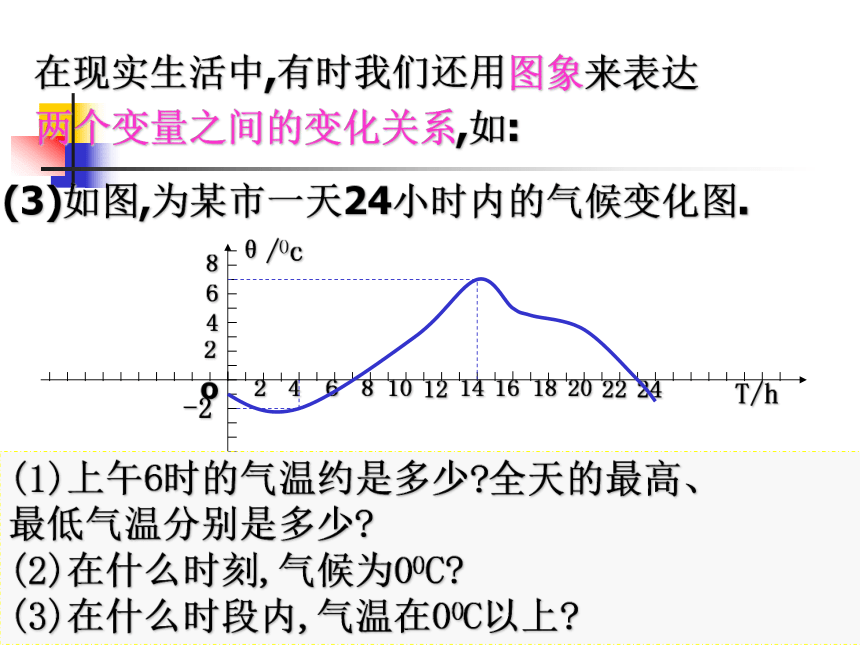
两个变量之间的变化关系,如:(3)如图,为某市一天24小时内的气候变化图.(1)上午6时的气温约是多少?全天的最高、
最低气温分别是多少?
(2)在什么时刻,气候为00C?
(3)在什么时段内,气温在00C以上?函数的定义: 一般地,设A,B是两个非空的数集,如果按
某种对应法则f,对于集合A中的每一个元数x,
在集合B中都有唯一确定的元素与它对应,这样
的对应叫做从A到B的一个函数(functin),
通常记为: y=f(x),x∈A.
其中,所有的输入值x组成的集合A叫做函数y=f(x)
的定义域(domain).
所有的输出值y组成的集合B叫做函数y=f(x)
的值域(range).(1)对于变量x允许取的每一个值组成的集合A
为函数y=f(x)的定义域.对于函数的意义,应从以下几个方面去理解:(2)变量x与y有确定的对应关系,即对于x允许
取的每一个值,y都有唯一确定的值与它对应。(2)对于变量y可能取到的每一个值组成的集合B为函数y=f(x)的值域.例1:根据函数的定义判断下列对应是否为函数: 例2:求下列函数的定义域: 例3:比较下面两个函数的定义域与值域: (1)f(x)=(x-1)2+1 ,x ∈{-1,0,1,2,3}(2)f(x)=(x-1)2+1怎样理解相同的函数: 由函数的概念可以知道,若变量x与变量y之间
有着某种特殊的对应关系(即对应法则),且变
量x在它的取值范围内任取一个值,变量y都有唯
一确定的值与它对应,则变量y是变量x的函数。也就是说,函数的概念中包含了以下两个方面
的内容:(1)y与x之间的函数关系式;(2)函数关系式中自变量x的取值范围。这就是说,相同的函数必须要求以上两个方面
都满足,即函数关系式相同(或变形后相同),
自变量x的取值范围也相同,否则,就不是相同
的函数。而其中函数关系式相同与否比较容易
注意到,自变量x的取值范围有时容易忽视,这
点请同学们注意。 怎样理解相同的函数:例4:下列函数中,与y=x表示是同一函数关系的是( )练习(课本):P24 1,2,3,4作业(课本) :5,6,7下课!
两个变量之间依赖关系的数学模型. 设在某变化过程中有两个变量x,y。如果
对于x在某一范围内的每一个确定的值,y都有
唯一确定的值与它对应,那么就说y是x的函数,
x叫做自变量。在现实生活中,我们可能会遇到下列问题:(1)我国人口随年份的变化而变化,如:你根据这个表说出在这几年中我国人口的变化情吗?这是通过1969—1999年我国人口数据表来体现
人口随年份的变化而变化在现实生活中,我们可能会遇到下列问题:(2)一物体从静止开始下落,下落的距离y(m)与
下落时间x(s)之间近似地满足关系式y=4.9x2.若一物体下落2s,你能求出它下落的距离吗?这是通过代数表达式来体现:
距离随时间的变化而变化在现实生活中,有时我们还用图象来表达
两个变量之间的变化关系,如:(3)如图,为某市一天24小时内的气候变化图.(1)上午6时的气温约是多少?全天的最高、
最低气温分别是多少?
(2)在什么时刻,气候为00C?
(3)在什么时段内,气温在00C以上?函数的定义: 一般地,设A,B是两个非空的数集,如果按
某种对应法则f,对于集合A中的每一个元数x,
在集合B中都有唯一确定的元素与它对应,这样
的对应叫做从A到B的一个函数(functin),
通常记为: y=f(x),x∈A.
其中,所有的输入值x组成的集合A叫做函数y=f(x)
的定义域(domain).
所有的输出值y组成的集合B叫做函数y=f(x)
的值域(range).(1)对于变量x允许取的每一个值组成的集合A
为函数y=f(x)的定义域.对于函数的意义,应从以下几个方面去理解:(2)变量x与y有确定的对应关系,即对于x允许
取的每一个值,y都有唯一确定的值与它对应。(2)对于变量y可能取到的每一个值组成的集合B为函数y=f(x)的值域.例1:根据函数的定义判断下列对应是否为函数: 例2:求下列函数的定义域: 例3:比较下面两个函数的定义域与值域: (1)f(x)=(x-1)2+1 ,x ∈{-1,0,1,2,3}(2)f(x)=(x-1)2+1怎样理解相同的函数: 由函数的概念可以知道,若变量x与变量y之间
有着某种特殊的对应关系(即对应法则),且变
量x在它的取值范围内任取一个值,变量y都有唯
一确定的值与它对应,则变量y是变量x的函数。也就是说,函数的概念中包含了以下两个方面
的内容:(1)y与x之间的函数关系式;(2)函数关系式中自变量x的取值范围。这就是说,相同的函数必须要求以上两个方面
都满足,即函数关系式相同(或变形后相同),
自变量x的取值范围也相同,否则,就不是相同
的函数。而其中函数关系式相同与否比较容易
注意到,自变量x的取值范围有时容易忽视,这
点请同学们注意。 怎样理解相同的函数:例4:下列函数中,与y=x表示是同一函数关系的是( )练习(课本):P24 1,2,3,4作业(课本) :5,6,7下课!
