青岛版数学七年级上册 7.4 第3课时 行程问题 课件(共20张PPT)
文档属性
| 名称 | 青岛版数学七年级上册 7.4 第3课时 行程问题 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-27 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第7章 一元一次方程
7.4 一元一次方程的应用
第3课时 行程问题
学习目标
能分析行程问题中的数量关系,并列出一元一次方
进一步掌握路程、时间与速度三个量之间的关系式
会用“图示法”分析行程问题中的数量关系,培养
分析问题、解决问题的能力
程解实际问题
速度、时间和路程之间有什么关系?
行程问题
路程=速度×时间;
速度=路程÷时间.
时间=路程÷速度;
相遇问题的探究
甲、乙两站相距480千米,一列慢车从甲站开出,每小时行90千米,一列快车从乙站开出,每小时行140千米.
(1)若慢车先开出1小时,快车再开,两车相向而行,快车开出多长时间后两车相遇?
设问题中的时间为x小时,根据题意,可画出示意图如下:
90×1
慢车x小时的行程
快车x小时的行程
甲站
乙站
相遇处
慢车
快车
480米
相遇问题的探究
(1)解:设快车开出x小时后两车相遇.
由题意,得140x+90(x+1)=480,即230x=390.
相遇问题的探究
相遇问题中等量关系的确定有三种角度:
(1)从时间角度考虑:两人同时出发,相遇时两人所用的时间相等
(3)从速度角度考虑:两人相向而行,他们的相对速度等于他们的速度之和
(2)从路程角度考虑:沿线段由两地相向而行,相遇时两人所走路程之和等于两地距离;沿圆周由同一地点背向而行,第一次相遇所走的路程和为圆周长
行程问题
对于一些比较直观的问题,可将题目中的条件以及它们之间的关系用简单明了的示意图表示出来,根据图示中有关数量的内在联系,找到相等关系,列出方程.图示法在解决行程类问题中应用较多.
甲、乙两站相距480千米,一列慢车从甲站开出,每小时行90千米,一列快车从乙站开出,每小时行140千米.
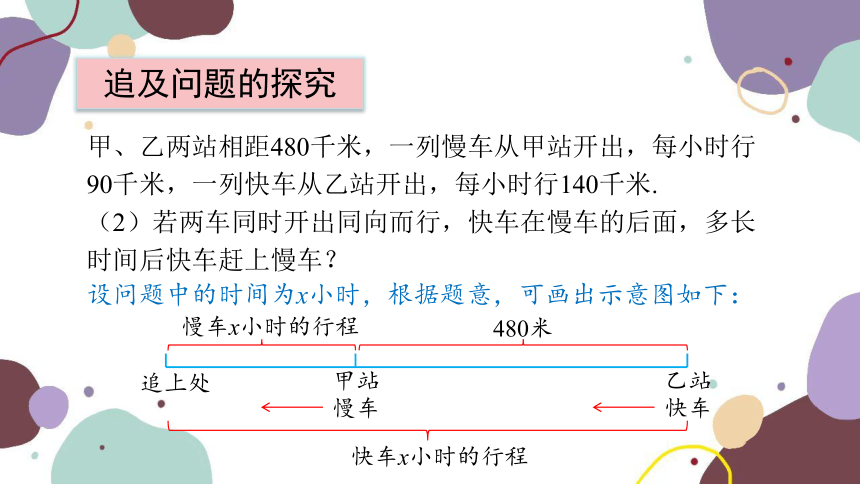
(2)若两车同时开出同向而行,快车在慢车的后面,多长时间后快车赶上慢车?
追及问题的探究
设问题中的时间为x小时,根据题意,可画出示意图如下:
慢车x小时的行程
快车x小时的行程
甲站
追上处
乙站
480米
慢车
快车
追及问题的探究
(2)设x小时后快车追上慢车.
所以,9.6小时后快车追上慢车.
经检验,x=9.6(小时)符合题意.
解这个方程,得x=9.6.
由题意,得140x=90x+480,即50x=480.
追及问题的探究
追及问题中的等量关系的确定方法分两种情形:
(1)同地不同时(如图):
慢者先行路程
B地
A地
C地
慢者被追及的路程
快者追及的路程
从时间角度考虑:
从路程角度考虑:
慢者所用时间-慢者先行时间=快者所用时间
慢者先行路程+慢者被追及的路程=快者追及的路程
追及问题的探究
追及问题中的等量关系的确定方法分两种情形:
(2)同时不同地(如图):
快慢者间的距离
B地
A地
C地
慢者所行的路程
快者所行的路程
从时间角度考虑:
从路程角度考虑:
从开始追赶到追上时,快者与慢者所用的时间相等
快慢者间的距离+慢者所行的路程=快者所行的路程
典例精讲
例3 某中学组织学生到校外参加义务植树活动.一部分学生骑自行车先走,速度为9千米/时;40分钟后其余学生乘汽车出发,速度为45千米/时,结果他们同时到达目的地.目的地距学校多少千米?
如果设目的地距学校x千米,你能填写下表吗?
路程/千米 速度/(千米/时) 时间/时
骑自行车
乘汽车
x
x
9
45
典例精讲
题目中的等量关系是_________________________;
骑自行车所用时间﹣乘汽车所用时间=___________.
时间=路程÷速度;
所以,目的地距学校7.5千米.
经检验,x=7.5(千米)符合题意.
解这个方程,得x=7.5.
航行问题的探究
一船从甲码头到乙码头顺流行驶,用了4小时;从乙码头返回甲码头逆流行驶,用了5小时.已知水流的速度是3千米/时,求船在静水中的速度.
分析:等量关系为:顺水速度×顺水时间=逆水速度×逆水时间
即4×(静水速度+水流速度)=5×(静水速度-水流速度)
解:设船在静水中的速度为x千米/时,则顺水速度为
所以船在静水中的速度为27千米/时.
经检验,x=27(千米/时)符合题意.
解这个方程,得x=27.
根据题意,得4(x+3)=5(x-3),
(x+3)千米/时,逆水速度为(x-3)千米/时.
航行问题的探究
关于航行问题中的顺水速度、逆水速度、静水速度和水流速度四者之间存在如下关系:
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
总结
类型 涉及的数量及公式 等量关系 注意事项
行程问题 相遇问题
追及问题
路程=速度×时间;
时间=路程÷速度;
速度=路程÷时间
快行程+慢行程=
总路程
快行程-慢行程=
原来相距的路程
相向而行,注意
出发时间、地点
同向而行,注意
出发时间、地点
类型 涉及的数量及公式 等量关系 注意事项
行程问题 航行问题
总结
顺水速度=静水速度
+水流速度;
逆水速度=静水速度
-水流速度
顺水路程=逆水
路程
两码头之间的距离、水流速度、船在静水中的速度不变
巩固练习
1.某行军纵队以9千米/时的速度行进,队尾的通讯员以15千米/时的速度赶到队伍前送一封信,送到后又立即返回队尾,共用20分钟,求这支队伍的长度.
解:设通讯员从队尾把信送到队头用x小时,则立即返回队尾
所以这支队伍的长度为1.6千米.
所以(15-9)x=1.6.
巩固练习
2.甲、乙两人环湖竞走,湖的周长为400米,乙的速度是80米/分,甲的速度是乙的速度的1.25倍,且甲在乙的前面100米处.如果两人同时同向出发,那么多长时间后两人第一次相遇?
解:设x分后两人第一次相遇.
所以,15分后两人第一次相遇.
经检验,x=15(分)符合题意.
解得x=15.
根据题意,得80x+300=80×1.25x,
巩固练习
3.一架飞机飞行在两城市之间,顺风需要2小时45分钟,逆风需要3小时,已知风速是20千米/时,求这两座城市之间的距离.
解:设飞机在无风的条件下的速度为x千米/时.
所以,这两座城市之间的距离为1320千米.
此时,(x-20) ×3=(460-20) ×3=1320.
经检验,x=460(千米)符合题意.
解得x=460.
根据两城市之间的路程不变,列方程,得
第7章 一元一次方程
7.4 一元一次方程的应用
第3课时 行程问题
学习目标
能分析行程问题中的数量关系,并列出一元一次方
进一步掌握路程、时间与速度三个量之间的关系式
会用“图示法”分析行程问题中的数量关系,培养
分析问题、解决问题的能力
程解实际问题
速度、时间和路程之间有什么关系?
行程问题
路程=速度×时间;
速度=路程÷时间.
时间=路程÷速度;
相遇问题的探究
甲、乙两站相距480千米,一列慢车从甲站开出,每小时行90千米,一列快车从乙站开出,每小时行140千米.
(1)若慢车先开出1小时,快车再开,两车相向而行,快车开出多长时间后两车相遇?
设问题中的时间为x小时,根据题意,可画出示意图如下:
90×1
慢车x小时的行程
快车x小时的行程
甲站
乙站
相遇处
慢车
快车
480米
相遇问题的探究
(1)解:设快车开出x小时后两车相遇.
由题意,得140x+90(x+1)=480,即230x=390.
相遇问题的探究
相遇问题中等量关系的确定有三种角度:
(1)从时间角度考虑:两人同时出发,相遇时两人所用的时间相等
(3)从速度角度考虑:两人相向而行,他们的相对速度等于他们的速度之和
(2)从路程角度考虑:沿线段由两地相向而行,相遇时两人所走路程之和等于两地距离;沿圆周由同一地点背向而行,第一次相遇所走的路程和为圆周长
行程问题
对于一些比较直观的问题,可将题目中的条件以及它们之间的关系用简单明了的示意图表示出来,根据图示中有关数量的内在联系,找到相等关系,列出方程.图示法在解决行程类问题中应用较多.
甲、乙两站相距480千米,一列慢车从甲站开出,每小时行90千米,一列快车从乙站开出,每小时行140千米.
(2)若两车同时开出同向而行,快车在慢车的后面,多长时间后快车赶上慢车?
追及问题的探究
设问题中的时间为x小时,根据题意,可画出示意图如下:
慢车x小时的行程
快车x小时的行程
甲站
追上处
乙站
480米
慢车
快车
追及问题的探究
(2)设x小时后快车追上慢车.
所以,9.6小时后快车追上慢车.
经检验,x=9.6(小时)符合题意.
解这个方程,得x=9.6.
由题意,得140x=90x+480,即50x=480.
追及问题的探究
追及问题中的等量关系的确定方法分两种情形:
(1)同地不同时(如图):
慢者先行路程
B地
A地
C地
慢者被追及的路程
快者追及的路程
从时间角度考虑:
从路程角度考虑:
慢者所用时间-慢者先行时间=快者所用时间
慢者先行路程+慢者被追及的路程=快者追及的路程
追及问题的探究
追及问题中的等量关系的确定方法分两种情形:
(2)同时不同地(如图):
快慢者间的距离
B地
A地
C地
慢者所行的路程
快者所行的路程
从时间角度考虑:
从路程角度考虑:
从开始追赶到追上时,快者与慢者所用的时间相等
快慢者间的距离+慢者所行的路程=快者所行的路程
典例精讲
例3 某中学组织学生到校外参加义务植树活动.一部分学生骑自行车先走,速度为9千米/时;40分钟后其余学生乘汽车出发,速度为45千米/时,结果他们同时到达目的地.目的地距学校多少千米?
如果设目的地距学校x千米,你能填写下表吗?
路程/千米 速度/(千米/时) 时间/时
骑自行车
乘汽车
x
x
9
45
典例精讲
题目中的等量关系是_________________________;
骑自行车所用时间﹣乘汽车所用时间=___________.
时间=路程÷速度;
所以,目的地距学校7.5千米.
经检验,x=7.5(千米)符合题意.
解这个方程,得x=7.5.
航行问题的探究
一船从甲码头到乙码头顺流行驶,用了4小时;从乙码头返回甲码头逆流行驶,用了5小时.已知水流的速度是3千米/时,求船在静水中的速度.
分析:等量关系为:顺水速度×顺水时间=逆水速度×逆水时间
即4×(静水速度+水流速度)=5×(静水速度-水流速度)
解:设船在静水中的速度为x千米/时,则顺水速度为
所以船在静水中的速度为27千米/时.
经检验,x=27(千米/时)符合题意.
解这个方程,得x=27.
根据题意,得4(x+3)=5(x-3),
(x+3)千米/时,逆水速度为(x-3)千米/时.
航行问题的探究
关于航行问题中的顺水速度、逆水速度、静水速度和水流速度四者之间存在如下关系:
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
总结
类型 涉及的数量及公式 等量关系 注意事项
行程问题 相遇问题
追及问题
路程=速度×时间;
时间=路程÷速度;
速度=路程÷时间
快行程+慢行程=
总路程
快行程-慢行程=
原来相距的路程
相向而行,注意
出发时间、地点
同向而行,注意
出发时间、地点
类型 涉及的数量及公式 等量关系 注意事项
行程问题 航行问题
总结
顺水速度=静水速度
+水流速度;
逆水速度=静水速度
-水流速度
顺水路程=逆水
路程
两码头之间的距离、水流速度、船在静水中的速度不变
巩固练习
1.某行军纵队以9千米/时的速度行进,队尾的通讯员以15千米/时的速度赶到队伍前送一封信,送到后又立即返回队尾,共用20分钟,求这支队伍的长度.
解:设通讯员从队尾把信送到队头用x小时,则立即返回队尾
所以这支队伍的长度为1.6千米.
所以(15-9)x=1.6.
巩固练习
2.甲、乙两人环湖竞走,湖的周长为400米,乙的速度是80米/分,甲的速度是乙的速度的1.25倍,且甲在乙的前面100米处.如果两人同时同向出发,那么多长时间后两人第一次相遇?
解:设x分后两人第一次相遇.
所以,15分后两人第一次相遇.
经检验,x=15(分)符合题意.
解得x=15.
根据题意,得80x+300=80×1.25x,
巩固练习
3.一架飞机飞行在两城市之间,顺风需要2小时45分钟,逆风需要3小时,已知风速是20千米/时,求这两座城市之间的距离.
解:设飞机在无风的条件下的速度为x千米/时.
所以,这两座城市之间的距离为1320千米.
此时,(x-20) ×3=(460-20) ×3=1320.
经检验,x=460(千米)符合题意.
解得x=460.
根据两城市之间的路程不变,列方程,得
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
