数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算 课件(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算 课件(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 770.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-26 17:48:20 | ||
图片预览



文档简介
(共16张PPT)
选择性必修一目录
章节 内容
第一章 空间向量与立体几何
第二章 直线和圆的方程
第三章 圆锥曲线的方程
(椭圆、双曲线、抛物线)
XXXX学校 XXX
2023.09
1.1.1
空间向量及线性运算
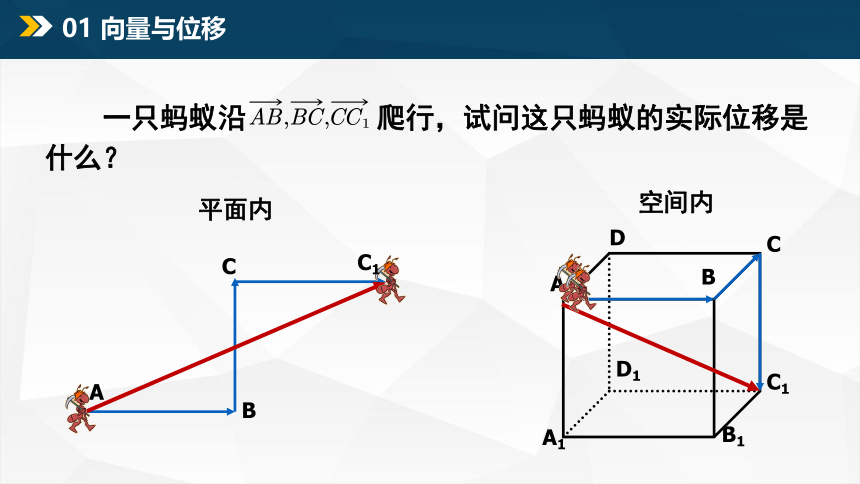
01 向量与位移
一只蚂蚁沿 爬行,试问这只蚂蚁的实际位移是什么?
A1
A
B
C
D
B1
C1
D1
A
B
C
C1
平面内
空间内
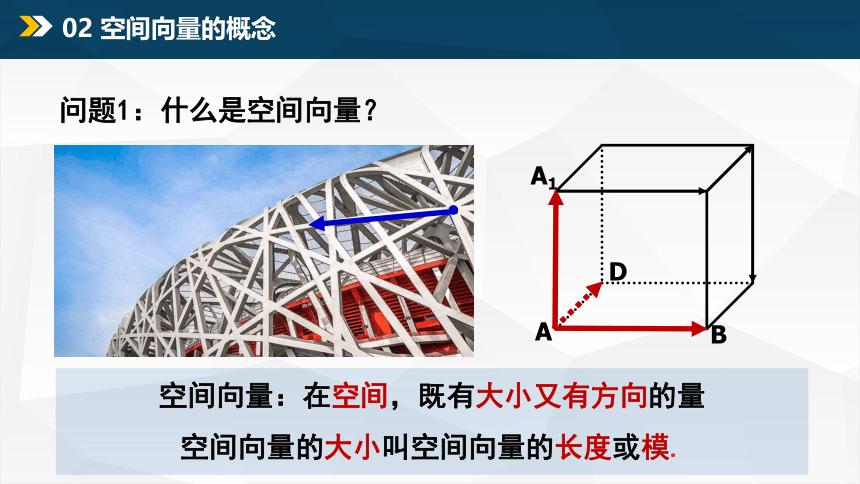
02 空间向量的概念
问题1:什么是空间向量?
A
A1
B
D
空间向量:在空间,既有大小又有方向的量
空间向量的大小叫空间向量的长度或模.
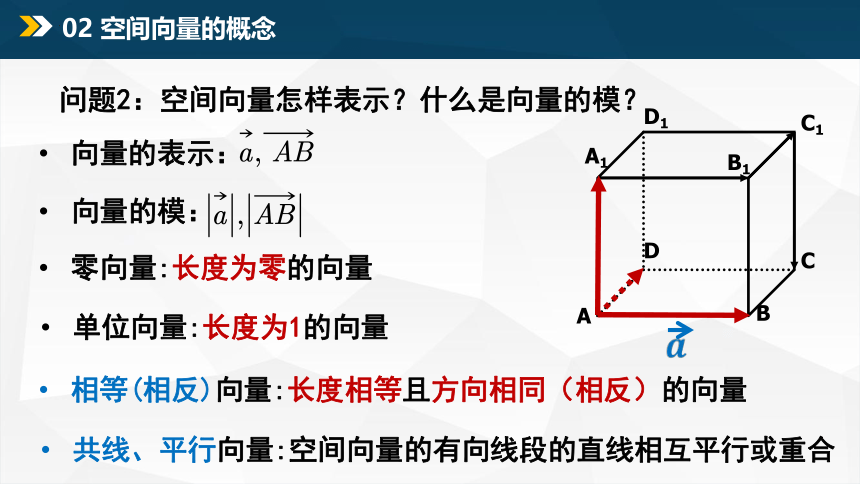
02 空间向量的概念
问题2:空间向量怎样表示?什么是向量的模?
向量的表示:
相等(相反)向量:长度相等且方向相同(相反)的向量
共线、平行向量:空间向量的有向线段的直线相互平行或重合
零向量:长度为零的向量
单位向量:长度为1的向量
向量的模:
A
A1
B1
C1
D1
B
C
D
03 概念辨析
(1)两个有共同起点且相等的向量,其终点必相同.( )
(2)两个有公共终点的向量,一定是共线向量.( )
(4)空间中方向相反的两个向量是相反向量.( )
(5)若A,B,C,D是不共线的四点,则 = 是四边形ABCD是平行四边形的充要条件.( )
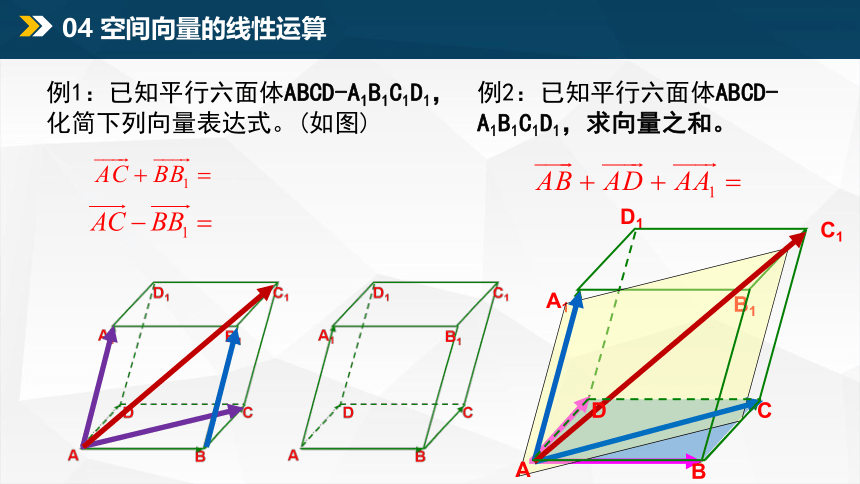
04 空间向量的线性运算
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量表达式。(如图)
例2:已知平行六面体ABCD-A1B1C1D1,求向量之和。
A1
B1
C1
D1
A
B
C
D
A
B
C
D
A1
B1
C1
D1
【探究】空间中,三个不共面的向量其和向量的几何意义是什么?
始点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量
04 空间向量的线性运算
结论
结合律:
平面的加法结合律、交换律在空间中仍然适用
a
b
a + b
(a + b) + c
a
a +( b + c)
b + c
b
c
c
交换律:
A
B
C
D
A’
B’
C’
D’
注:零向量与任意向量都共线.
1.空间共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,叫做共线(平行)向量,记作
2.空间共线向量定理:对空间任意两个向量
的充要条件是存在实数 使
方向向量
05 空间向量的共线与共面
a
b
a
b
O
A
B
b
结论:空间任意两个向量都是共面向量(平行于同一个平面)
思考:空间任意两个向量是否可平移至一个平面内?平面是否唯一确定?
05 空间向量的共线与共面
那么什么情况下三个向量共面呢?
如果空间向量 与两不共线向量 共面,那么可将三个向量平移到同一平面 ,则有
A
P
B
C
(A,B,C,P四点共面)
结论: 如果两个向量 不共线,那么向量 与向量 共面的充要条件是存在有序实数对x,y使
05 空间向量的共线与共面
【思考】
对任意一点O和不共线的三点A,B,C,且 , 则x+y+z=1是四点P,A,B,C共面的充要条件吗 为什么
A
P
B
C
O
选择性必修一目录
章节 内容
第一章 空间向量与立体几何
第二章 直线和圆的方程
第三章 圆锥曲线的方程
(椭圆、双曲线、抛物线)
XXXX学校 XXX
2023.09
1.1.1
空间向量及线性运算
01 向量与位移
一只蚂蚁沿 爬行,试问这只蚂蚁的实际位移是什么?
A1
A
B
C
D
B1
C1
D1
A
B
C
C1
平面内
空间内
02 空间向量的概念
问题1:什么是空间向量?
A
A1
B
D
空间向量:在空间,既有大小又有方向的量
空间向量的大小叫空间向量的长度或模.
02 空间向量的概念
问题2:空间向量怎样表示?什么是向量的模?
向量的表示:
相等(相反)向量:长度相等且方向相同(相反)的向量
共线、平行向量:空间向量的有向线段的直线相互平行或重合
零向量:长度为零的向量
单位向量:长度为1的向量
向量的模:
A
A1
B1
C1
D1
B
C
D
03 概念辨析
(1)两个有共同起点且相等的向量,其终点必相同.( )
(2)两个有公共终点的向量,一定是共线向量.( )
(4)空间中方向相反的两个向量是相反向量.( )
(5)若A,B,C,D是不共线的四点,则 = 是四边形ABCD是平行四边形的充要条件.( )
04 空间向量的线性运算
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量表达式。(如图)
例2:已知平行六面体ABCD-A1B1C1D1,求向量之和。
A1
B1
C1
D1
A
B
C
D
A
B
C
D
A1
B1
C1
D1
【探究】空间中,三个不共面的向量其和向量的几何意义是什么?
始点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量
04 空间向量的线性运算
结论
结合律:
平面的加法结合律、交换律在空间中仍然适用
a
b
a + b
(a + b) + c
a
a +( b + c)
b + c
b
c
c
交换律:
A
B
C
D
A’
B’
C’
D’
注:零向量与任意向量都共线.
1.空间共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,叫做共线(平行)向量,记作
2.空间共线向量定理:对空间任意两个向量
的充要条件是存在实数 使
方向向量
05 空间向量的共线与共面
a
b
a
b
O
A
B
b
结论:空间任意两个向量都是共面向量(平行于同一个平面)
思考:空间任意两个向量是否可平移至一个平面内?平面是否唯一确定?
05 空间向量的共线与共面
那么什么情况下三个向量共面呢?
如果空间向量 与两不共线向量 共面,那么可将三个向量平移到同一平面 ,则有
A
P
B
C
(A,B,C,P四点共面)
结论: 如果两个向量 不共线,那么向量 与向量 共面的充要条件是存在有序实数对x,y使
05 空间向量的共线与共面
【思考】
对任意一点O和不共线的三点A,B,C,且 , 则x+y+z=1是四点P,A,B,C共面的充要条件吗 为什么
A
P
B
C
O
