1.4.2 立体几何中的向量方法(距离、角度) 课件(共26张PPT)
文档属性
| 名称 | 1.4.2 立体几何中的向量方法(距离、角度) 课件(共26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 968.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-26 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
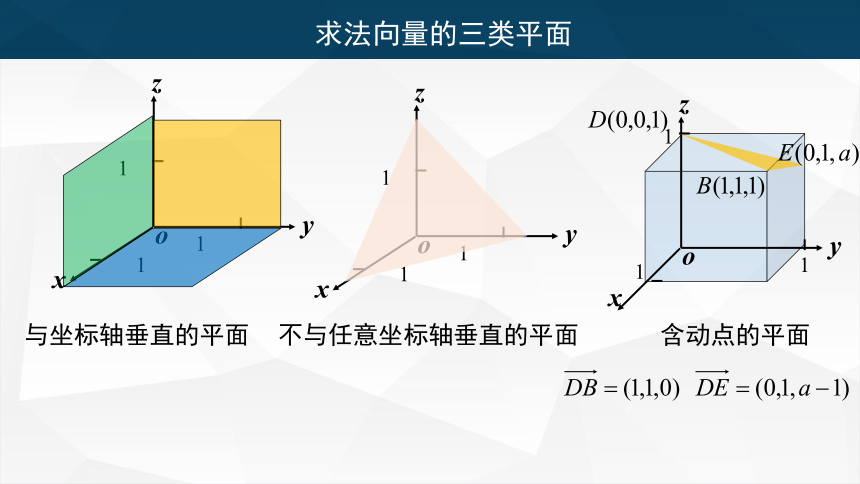
求法向量的三类平面
1
1
1
与坐标轴垂直的平面
1
1
1
不与任意坐标轴垂直的平面
1
1
1
含动点的平面
1.2
立体几何中的向量方法(距离)
XXXX学校 XXX
2023.09
P
A
Q
l
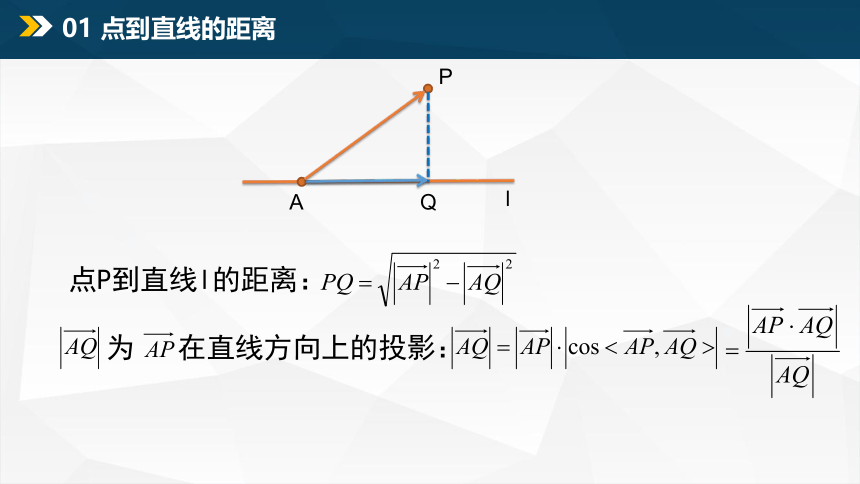
点P到直线l的距离:
为 在直线方向上的投影:
01 点到直线的距离
02 点到面的距离
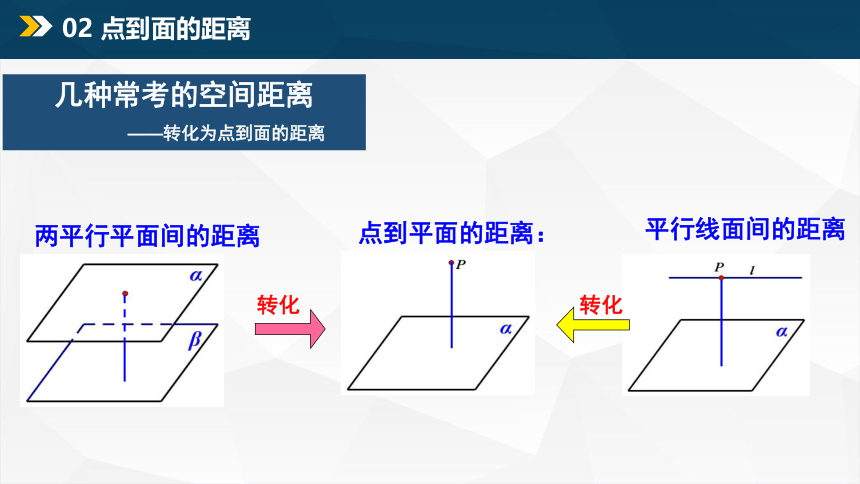
几种常考的空间距离
——转化为点到面的距离
点到平面的距离:
平行线面间的距离
两平行平面间的距离
转化
转化
02 点到面的距离
探究:如何从数量积的角度求点到平面的距离
这个是距离吗?
在平面法向量上投影的绝对值
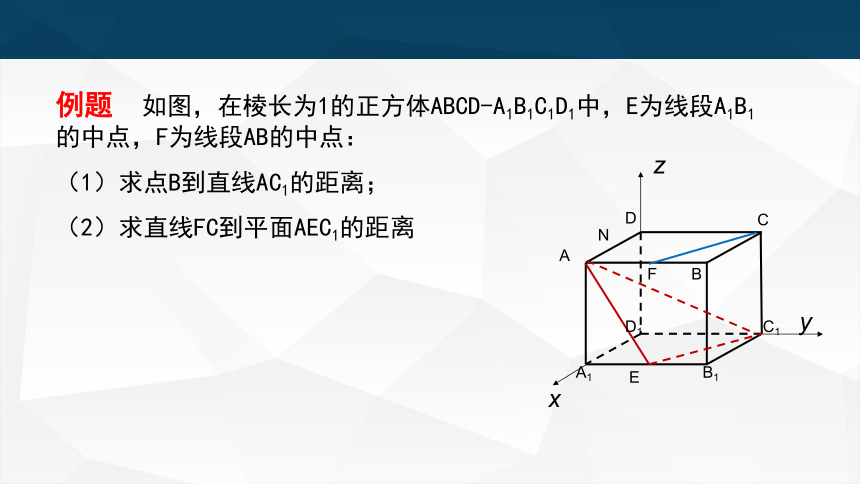
例题 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点:
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离
A1
B1
C1
D1
A
B
C
D
N
E
F
x
y
z
类型一 用空间向量求距离
【典例】已知四边形ABCD是边长为4的正方形,E,F分别是边AB,AD的中点,CG垂直于正方形ABCD所在的平面,且CG=2,求:
(1)点B到直线FG的距离;
(2)点B到平面EFG的距离.
【习练·破】
已知三棱锥O-ABC,OA⊥OB,OB⊥OC,OC⊥OA,且OA=1,OB=2,OC=2,则点A到直线BC的距离为 ( )
练习 在边长为1的正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点,求点A与平面EFDB的距离。
A
B
C
D
A1
B1
C1
D1
M
N
E
F
x
y
z
可以选择点B作为平面内一点,计算点A与平面EFDB的距离
1.4.2 立体几何中的向量方法
——角度问题
l
m
l
m
03 异面直线所成角
【习练·破】
已知四棱锥S-ABCD的底面是正方形且侧棱长与底面边长都相等,E是SB的中点,则AE,SD所成的角的余弦值为 ( )
类型二 向量法求两异面直线所成的角
【典例】正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1C1的中点,求异面直线AE与CF所成角的余弦值.
l
l
04 线面所成角
类型三 向量法求线面角、平面的夹角 角度1 向量法求线面角
【典例】 如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC= AB,
N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小.
【素养·探】
将本例改为:四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M
为线段AD上一点,AM=2MD,N为PC的中点,求直线AN与平面PMN所成角的正弦值.
两个平面的法向量所成角是这两个平面的夹角吗?
05 平面与平面所成角
例题 如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1,求平面PQR与平面A1B1C1夹角的余弦值
A1
B1
C1
Q
A
B
C
R
P
x
y
z
4.如图,△ABC和△DBC所在平面垂直,且AB=BC=BD,∠CBA=∠DBC=120°.求:
(1)直线AD与BC所成角的大小;
(2)直线AD与平面BCD所成角的大小;
(3)平面ABD和平面BDC的夹角的余弦值.
D
B
A
C
角度2 向量法求平面的夹角
【典例】如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求平面APB与平面PBC夹角的余弦值.
【习练·破】
如图,直三棱柱ABC-A1B1C1中,AC=BC= AA1,D是棱AA1的中点,DC1⊥BD,
(1)证明:DC1⊥BC.
(2)求平面A1B1BD与平面C1BD的夹角的大小.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
(2)求证:PB垂直平面EFD;
(3)求平面CPB与平面PBD的夹角的大小.
C
P
A
B
D
E
F
求法向量的三类平面
1
1
1
与坐标轴垂直的平面
1
1
1
不与任意坐标轴垂直的平面
1
1
1
含动点的平面
1.2
立体几何中的向量方法(距离)
XXXX学校 XXX
2023.09
P
A
Q
l
点P到直线l的距离:
为 在直线方向上的投影:
01 点到直线的距离
02 点到面的距离
几种常考的空间距离
——转化为点到面的距离
点到平面的距离:
平行线面间的距离
两平行平面间的距离
转化
转化
02 点到面的距离
探究:如何从数量积的角度求点到平面的距离
这个是距离吗?
在平面法向量上投影的绝对值
例题 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点:
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离
A1
B1
C1
D1
A
B
C
D
N
E
F
x
y
z
类型一 用空间向量求距离
【典例】已知四边形ABCD是边长为4的正方形,E,F分别是边AB,AD的中点,CG垂直于正方形ABCD所在的平面,且CG=2,求:
(1)点B到直线FG的距离;
(2)点B到平面EFG的距离.
【习练·破】
已知三棱锥O-ABC,OA⊥OB,OB⊥OC,OC⊥OA,且OA=1,OB=2,OC=2,则点A到直线BC的距离为 ( )
练习 在边长为1的正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点,求点A与平面EFDB的距离。
A
B
C
D
A1
B1
C1
D1
M
N
E
F
x
y
z
可以选择点B作为平面内一点,计算点A与平面EFDB的距离
1.4.2 立体几何中的向量方法
——角度问题
l
m
l
m
03 异面直线所成角
【习练·破】
已知四棱锥S-ABCD的底面是正方形且侧棱长与底面边长都相等,E是SB的中点,则AE,SD所成的角的余弦值为 ( )
类型二 向量法求两异面直线所成的角
【典例】正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1C1的中点,求异面直线AE与CF所成角的余弦值.
l
l
04 线面所成角
类型三 向量法求线面角、平面的夹角 角度1 向量法求线面角
【典例】 如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC= AB,
N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小.
【素养·探】
将本例改为:四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M
为线段AD上一点,AM=2MD,N为PC的中点,求直线AN与平面PMN所成角的正弦值.
两个平面的法向量所成角是这两个平面的夹角吗?
05 平面与平面所成角
例题 如图,在直三棱柱ABC-A1B1C1中,AC=CB=2,AA1=3,∠ACB=90°,P为BC中点,点Q,R分别在棱AA1,BB1上,A1Q=2AQ,BR=2RB1,求平面PQR与平面A1B1C1夹角的余弦值
A1
B1
C1
Q
A
B
C
R
P
x
y
z
4.如图,△ABC和△DBC所在平面垂直,且AB=BC=BD,∠CBA=∠DBC=120°.求:
(1)直线AD与BC所成角的大小;
(2)直线AD与平面BCD所成角的大小;
(3)平面ABD和平面BDC的夹角的余弦值.
D
B
A
C
角度2 向量法求平面的夹角
【典例】如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求平面APB与平面PBC夹角的余弦值.
【习练·破】
如图,直三棱柱ABC-A1B1C1中,AC=BC= AA1,D是棱AA1的中点,DC1⊥BD,
(1)证明:DC1⊥BC.
(2)求平面A1B1BD与平面C1BD的夹角的大小.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
(2)求证:PB垂直平面EFD;
(3)求平面CPB与平面PBD的夹角的大小.
C
P
A
B
D
E
F
