等腰三角形[上学期]
图片预览







文档简介
课件30张PPT。3.12等腰三角形的性质哈 五 中
初 中 组
荀 辉三角形等腰三角形不等边三角形等边三角形
底边和腰不相等的等腰三角形
3.12等腰三角形的性质打开知识的大门等腰三角形的两个底角相等。 ) 底角 (顶角
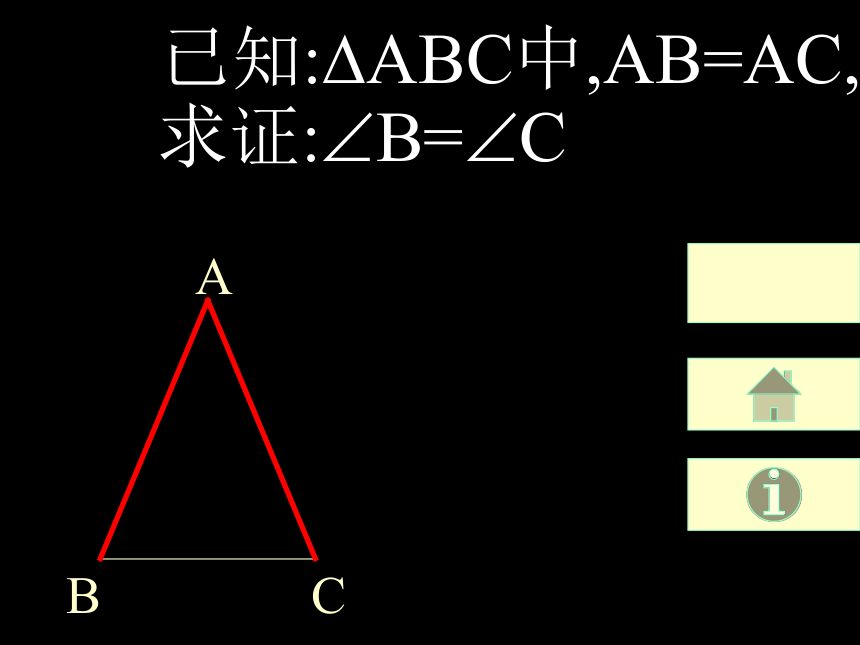
已知:?ABC中,AB=AC,
求证:?B=?C已知:?ABC中,AB=AC,
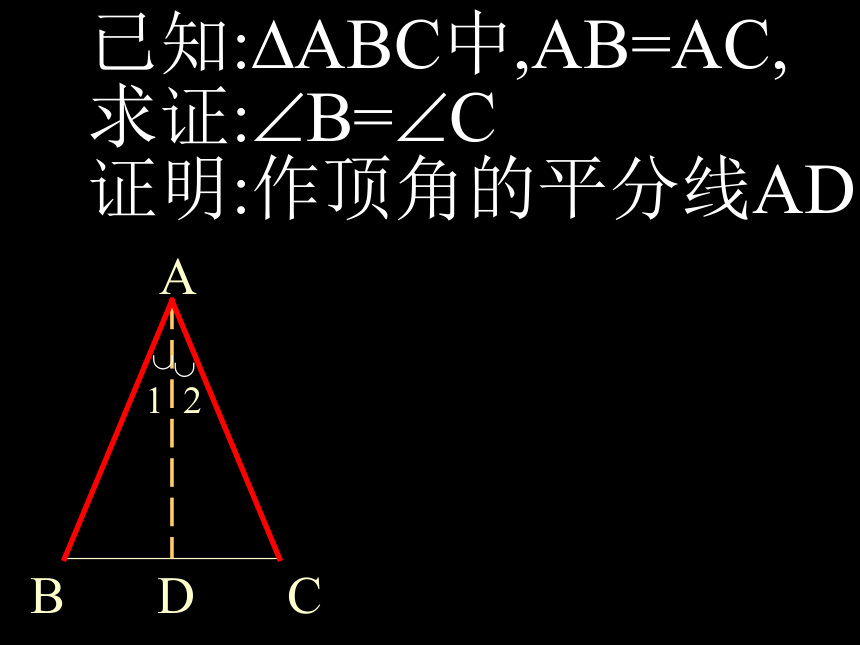
求证:?B=?C证明:作顶角的平分线AD 等腰三角形的性质定理(简记成“等边对等角”)等腰三角形的两个底角相等。 ) 底角 (顶角
已知:?ABC中,AB=AC,
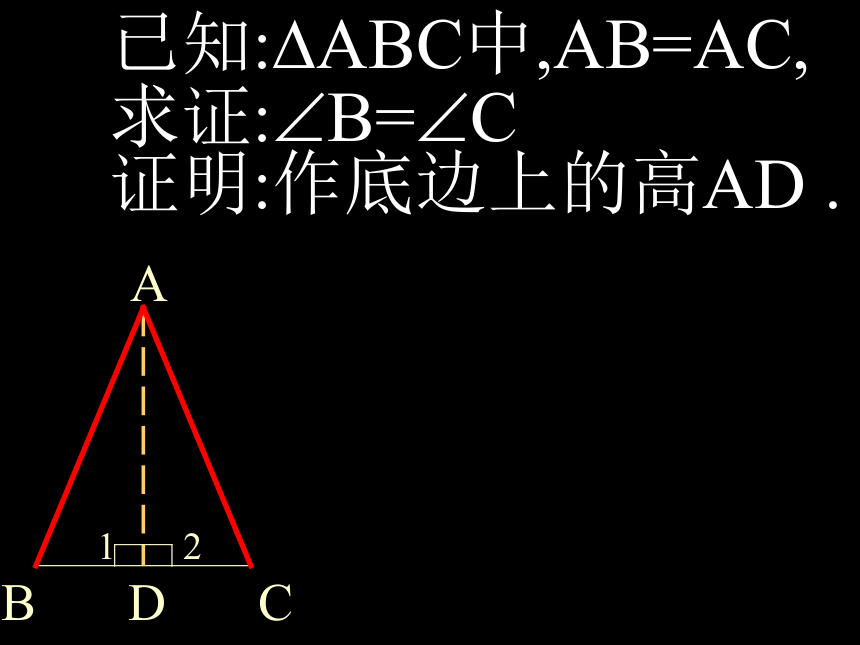
求证:?B=?C证明:作底边上的高AD .证明:作底边上的高AD .? ?1= ?2=90?在Rt?BAD和Rt?CAD中,AB=AC(已知)AD=AD(公共边) ? ?B= ?C 证明:作底边上的中线
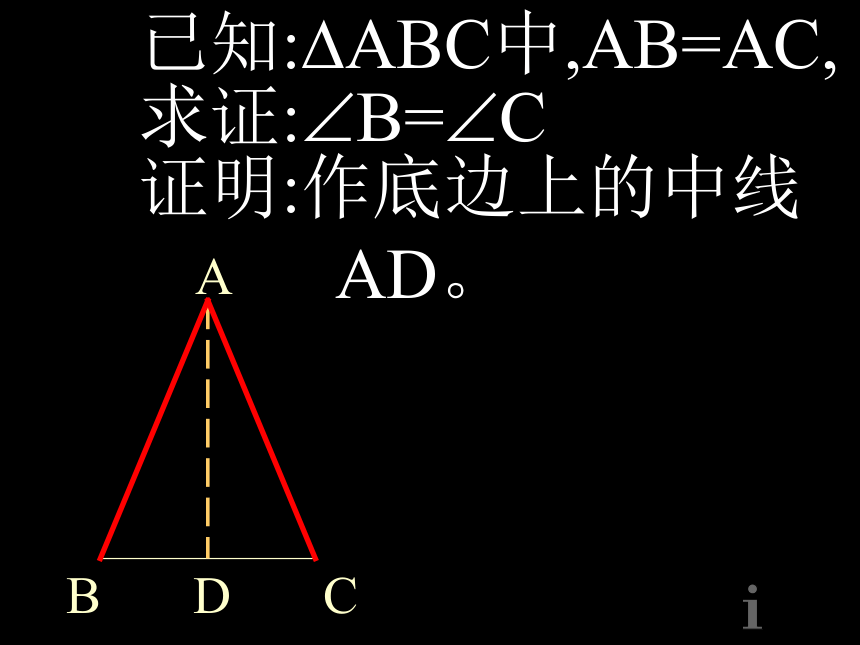
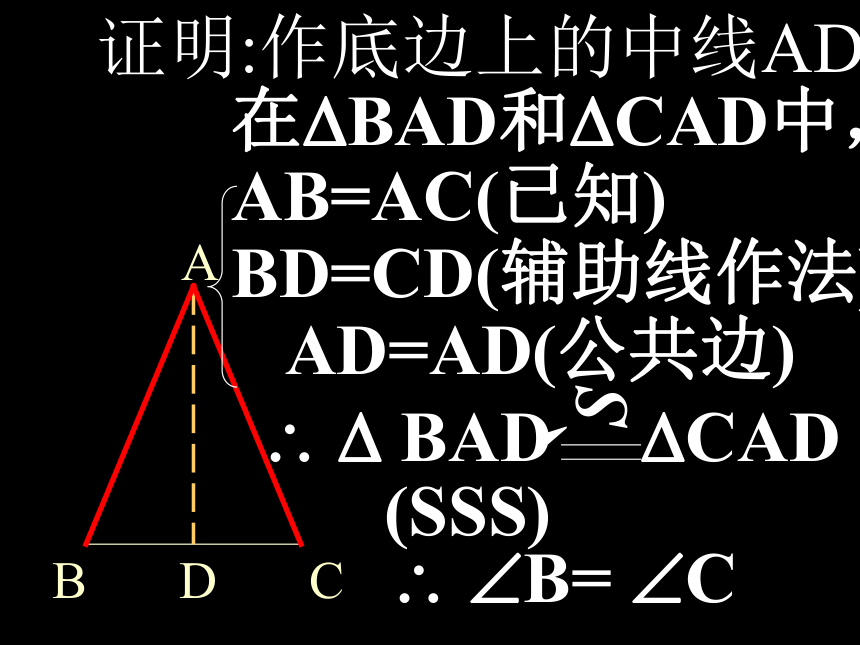
AD。已知:?ABC中,AB=AC,
求证:?B=?CAB=AC(已知)
BD=CD(辅助线作法)
AD=AD(公共边)
在?BAD和?CAD中, ? ?B= ?C证明:作底边上的中线AD练习1.
怎样从等腰三角形的性质定理得出推论:等腰直角三角形的每一个锐角都等于45 ?。练习2.
等腰三角形的一个底角
等于75 ?,那么它
的顶角等于多
少度。30 ?.练习3.
等腰三角形的一个 角
等于75 ?,那么另外
的 角等于多
少度。30 ?52.5?
解:练习4. 已知?ABC中有一个角是100?,那么另外一个角的度数是多少。
100?40?解:?AD平分BC,
并且AD?BC。?BD=CD,
?ADB=?ADC=90?推论 1 等腰三角形顶角的平分线平分底边并且垂直底边。(等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。)练习5.根据等腰三角形性质定理的推论,在?ABC中,AB=AC时,BAD CADBD CD练习5.根据等腰三角形性质定理的推论,在?ABC中,AB=AC时,AD BCBAD CAD练习5.根据等腰三角形性质定理的推论,在?ABC中,AB=AC时,AD BC
BD CD练习6.
等腰直角三角形斜边上的高把直角分成两个角,这两个角的度数。45? 45? 推论2 等边三角形的各角都相等,并且每一个
角都等于60?。例1 已知:如图,房屋的顶角? BAC=100 ?,过屋顶A的立柱AD?BC,屋椽AB=AC.求顶架上?B, ?C,
?BAD, ?CAD
的度数。??BAD=?CAD=50 ?。解:在?ABC中??B=?C(等边对等角)??B=?C=1/2(180-?A)
=40???BAD=?CAD练习7.
已知?ABC是等边三角形,AD是高,画出图形,说出图中?BAC,?BAD, ?B, ?C的度数 。思考题:已知:如图在?ABC中,AB=AC,
点D在AC上,且
BD=BC=AD.
求?ABC各
角的度数.D预习作业:69页等腰三角形的性质
复习作业:72页2,3.
初 中 组
荀 辉三角形等腰三角形不等边三角形等边三角形
底边和腰不相等的等腰三角形
3.12等腰三角形的性质打开知识的大门等腰三角形的两个底角相等。 ) 底角 (顶角
已知:?ABC中,AB=AC,
求证:?B=?C已知:?ABC中,AB=AC,
求证:?B=?C证明:作顶角的平分线AD 等腰三角形的性质定理(简记成“等边对等角”)等腰三角形的两个底角相等。 ) 底角 (顶角
已知:?ABC中,AB=AC,
求证:?B=?C证明:作底边上的高AD .证明:作底边上的高AD .? ?1= ?2=90?在Rt?BAD和Rt?CAD中,AB=AC(已知)AD=AD(公共边) ? ?B= ?C 证明:作底边上的中线
AD。已知:?ABC中,AB=AC,
求证:?B=?CAB=AC(已知)
BD=CD(辅助线作法)
AD=AD(公共边)
在?BAD和?CAD中, ? ?B= ?C证明:作底边上的中线AD练习1.
怎样从等腰三角形的性质定理得出推论:等腰直角三角形的每一个锐角都等于45 ?。练习2.
等腰三角形的一个底角
等于75 ?,那么它
的顶角等于多
少度。30 ?.练习3.
等腰三角形的一个 角
等于75 ?,那么另外
的 角等于多
少度。30 ?52.5?
解:练习4. 已知?ABC中有一个角是100?,那么另外一个角的度数是多少。
100?40?解:?AD平分BC,
并且AD?BC。?BD=CD,
?ADB=?ADC=90?推论 1 等腰三角形顶角的平分线平分底边并且垂直底边。(等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。)练习5.根据等腰三角形性质定理的推论,在?ABC中,AB=AC时,BAD CADBD CD练习5.根据等腰三角形性质定理的推论,在?ABC中,AB=AC时,AD BCBAD CAD练习5.根据等腰三角形性质定理的推论,在?ABC中,AB=AC时,AD BC
BD CD练习6.
等腰直角三角形斜边上的高把直角分成两个角,这两个角的度数。45? 45? 推论2 等边三角形的各角都相等,并且每一个
角都等于60?。例1 已知:如图,房屋的顶角? BAC=100 ?,过屋顶A的立柱AD?BC,屋椽AB=AC.求顶架上?B, ?C,
?BAD, ?CAD
的度数。??BAD=?CAD=50 ?。解:在?ABC中??B=?C(等边对等角)??B=?C=1/2(180-?A)
=40???BAD=?CAD练习7.
已知?ABC是等边三角形,AD是高,画出图形,说出图中?BAC,?BAD, ?B, ?C的度数 。思考题:已知:如图在?ABC中,AB=AC,
点D在AC上,且
BD=BC=AD.
求?ABC各
角的度数.D预习作业:69页等腰三角形的性质
复习作业:72页2,3.
