数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算 课件(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-26 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
1.1.2
空间向量的数量积运算
一、基本概念
01 两个向量的夹角的定义
如图,已知两个非零向量 在空间任取一点0,作
,则∠AOB叫做向量 的夹角,记作: .
1.范围:
2.
3.如果 ,则称 相互垂直,并记作:
规定:零向量与任意向量的数量积等于零.
特别的,
02 两个向量的数量积
已知空间两个非零向量 ,则 叫做 的数量积,记作: .
数量积不满足结合律
02 数量积运算规律
若 都不为 数量积运算误区
数量积运算 可约吗?
可除吗? 若 ,则
可结合吗?
不可以
不可以
不可以
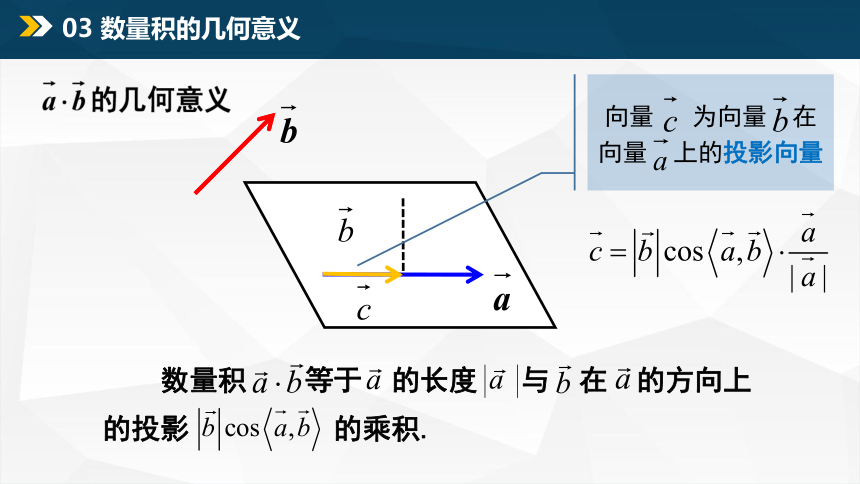
数量积 等于 的长度 与 在 的方向上的投影 的乘积.
向量 为向量 在向量 上的投影向量
03 数量积的几何意义
证明两向量垂直的依据
求向量的长度(模)的依据.
03 数量积的性质
对于任意的非零向量 :
数量积公式求夹角(简单型)
工具:
P4
P6
数量积公式证明垂直(90°)
A
A1
B1
C1
D1
B
C
D
证明:A1B⊥AC1
工具:
数量积公式证明垂直(90°)
数量积公式求夹角(复杂一丢丢型)
如图,在正三棱柱ABC-A1B1C1中,若AB= BB1,则AB1与BC1所成角的大小为_______
A1
B1
C1
A
B
C
在平行六面体ABCD-A'B'C'D'中,AB=4,AD=3,AA'=5,∠BAD=90°,∠BAA'=∠DAA'=60°. 求:AB’,AC'的长
A'
B'
C'
D'
A
B
C
D
变式:∠BAD=∠BAA'=∠DAA'=60°
类型三 空间向量数量积的应用
角度1 利用数量积证明空间中的垂直关系
【典例】 已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC,M,N
分别是OA,BC的中点,G是MN的中点,求证:OG⊥BC.
【思维·引】利用 表示出 ,证明 =0.
【素养·探】
利用数量积证明垂直,是空间向量的常见应用,常用到核心素养中的数学运算.若将典例改为:已知空间四边形ABCD中,AB⊥CD,AC⊥BD,求证:AD⊥BC.
角度2 利用数量积求距离
【典例】如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
A
B
C
D
A
B
C
D
【习练·破】
如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.
1.1.2
空间向量的数量积运算
一、基本概念
01 两个向量的夹角的定义
如图,已知两个非零向量 在空间任取一点0,作
,则∠AOB叫做向量 的夹角,记作: .
1.范围:
2.
3.如果 ,则称 相互垂直,并记作:
规定:零向量与任意向量的数量积等于零.
特别的,
02 两个向量的数量积
已知空间两个非零向量 ,则 叫做 的数量积,记作: .
数量积不满足结合律
02 数量积运算规律
若 都不为 数量积运算误区
数量积运算 可约吗?
可除吗? 若 ,则
可结合吗?
不可以
不可以
不可以
数量积 等于 的长度 与 在 的方向上的投影 的乘积.
向量 为向量 在向量 上的投影向量
03 数量积的几何意义
证明两向量垂直的依据
求向量的长度(模)的依据.
03 数量积的性质
对于任意的非零向量 :
数量积公式求夹角(简单型)
工具:
P4
P6
数量积公式证明垂直(90°)
A
A1
B1
C1
D1
B
C
D
证明:A1B⊥AC1
工具:
数量积公式证明垂直(90°)
数量积公式求夹角(复杂一丢丢型)
如图,在正三棱柱ABC-A1B1C1中,若AB= BB1,则AB1与BC1所成角的大小为_______
A1
B1
C1
A
B
C
在平行六面体ABCD-A'B'C'D'中,AB=4,AD=3,AA'=5,∠BAD=90°,∠BAA'=∠DAA'=60°. 求:AB’,AC'的长
A'
B'
C'
D'
A
B
C
D
变式:∠BAD=∠BAA'=∠DAA'=60°
类型三 空间向量数量积的应用
角度1 利用数量积证明空间中的垂直关系
【典例】 已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC,M,N
分别是OA,BC的中点,G是MN的中点,求证:OG⊥BC.
【思维·引】利用 表示出 ,证明 =0.
【素养·探】
利用数量积证明垂直,是空间向量的常见应用,常用到核心素养中的数学运算.若将典例改为:已知空间四边形ABCD中,AB⊥CD,AC⊥BD,求证:AD⊥BC.
角度2 利用数量积求距离
【典例】如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
A
B
C
D
A
B
C
D
【习练·破】
如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.
