新人教A版必修第二册第8章立体几何初步测评(含解析)
文档属性
| 名称 | 新人教A版必修第二册第8章立体几何初步测评(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 17:02:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章测评
(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列说法正确的是( )
A.圆锥的侧面展开图是一个等腰三角形
B.棱柱即是两个底面全等且其余各面都是矩形的多面体
C.任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
D.通过圆台侧面上一点,有无数条母线
2.如图所示,在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于( )
A.AC B.BD C.A1D D.A1D1
3.如图,Rt△O'A'B'是一平面图形的直观图,斜边O'B'=2,则这个平面图形的面积是( )
A B.1
C D.2
4.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何 ”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底面的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少 ”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )(“斛”不是国际通用单位)
A.14斛 B.22斛
C.36斛 D.66斛
5.如图,四棱锥S-ABCD所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A.2+ B.3+
C.3+2 D.2+2
6.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π
C.144π D.256π
7.已知平面α⊥平面β,α∩β=l,在l上取线段AB=4,AC,BD分别在平面α和平面β内,且AC⊥AB,DB⊥AB,AC=3,BD=12,则CD的长度为( )
A.13 B C.12 D.15
8.已知平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
A B
C D
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.用一个平面去截一个几何体,得到的截面是圆面,则这个几何体可能是( )
A.圆锥 B.圆柱
C.球 D.棱柱
10.已知直线l⊥平面α,直线m 平面β.则下列结论正确的是( )
A.α∥β l⊥m B.α⊥β l∥m
C.l∥m α⊥β D.l⊥m α∥β
11.一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,则下列结论正确的是( )
A.圆柱的侧面积为2πR2
B.圆锥的侧面积为2πR2
C.圆柱的侧面积与球的表面积相等
D.圆柱、圆锥、球的体积之比为3∶1∶2
12.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是 ( )
A.PB⊥AD
B.平面PAB⊥平面PBD
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
三、填空题:本题共4小题,每小题5分,共20分.
13.现有用橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2,高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为 .
14.在四面体A-BCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=,则异面直线AD与BC所成角的大小为 .
15.已知在四面体P-ABC中,PA=PB=4,PC=2,AC=2,PB⊥平面PAC,则四面体P-ABC外接球的体积为 .
16.如图,P是边长为2的正方形ABCD外一点,PA⊥AB,PA⊥BC,且PC=5,则直线BD与平面PAC的位置关系为 ,二面角P-BD-A的余弦值为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
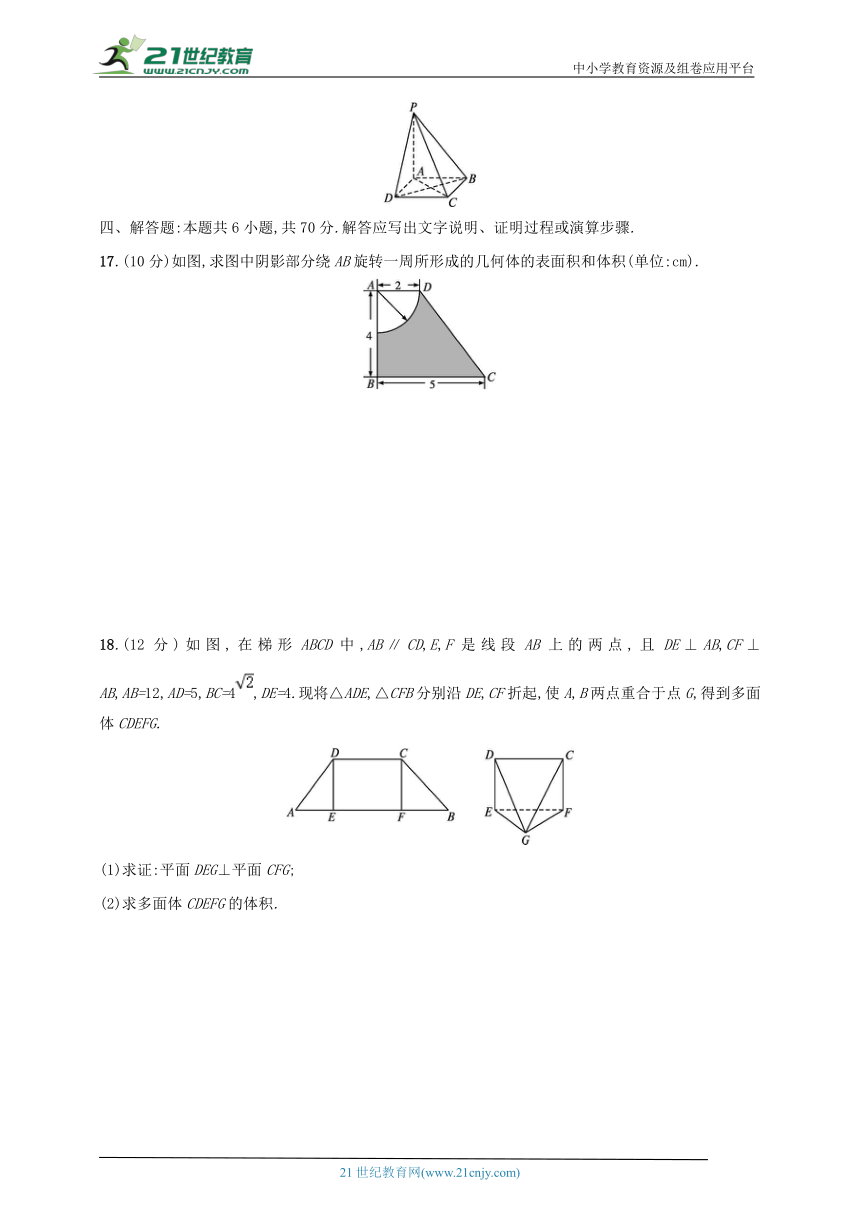
17.(10分)如图,求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积(单位:cm).
18.(12分)如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合于点G,得到多面体CDEFG.
(1)求证:平面DEG⊥平面CFG;
(2)求多面体CDEFG的体积.
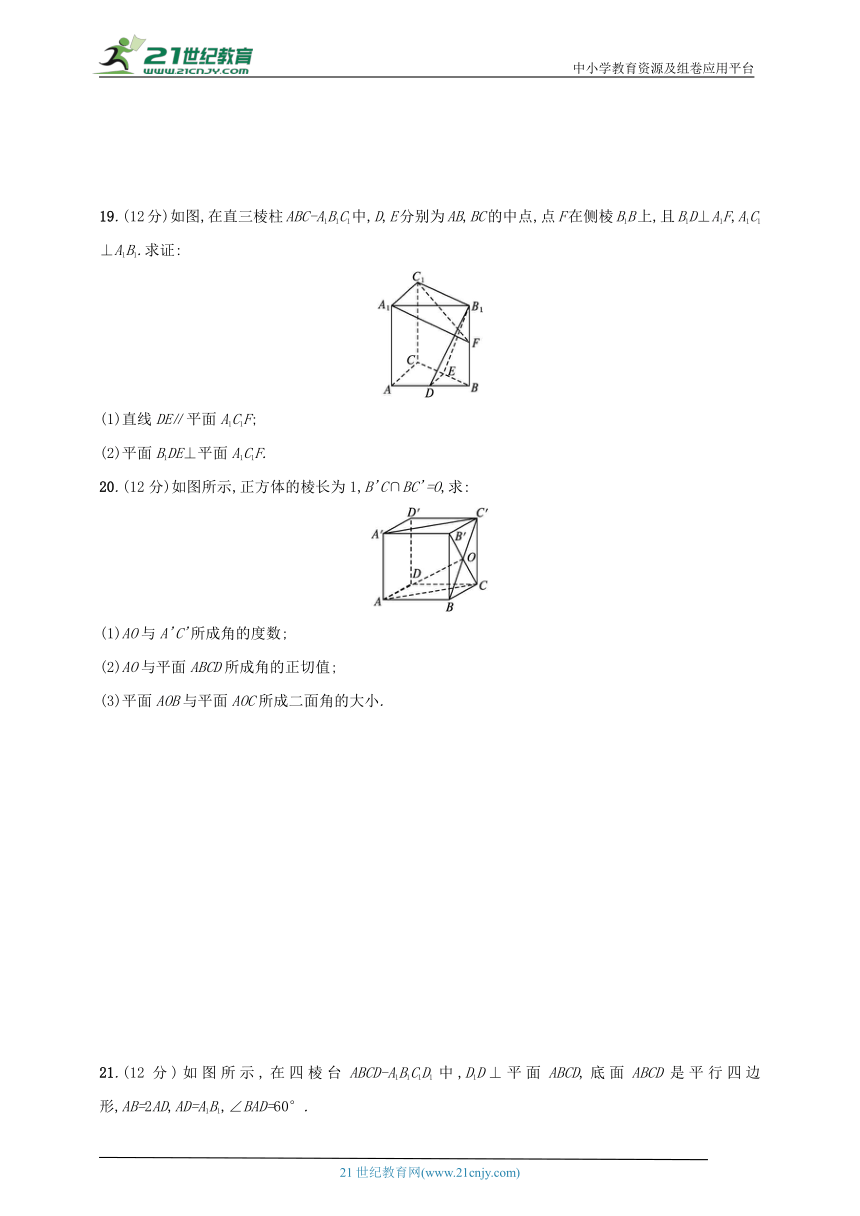
19.(12分)如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
20.(12分)如图所示,正方体的棱长为1,B'C∩BC'=O,求:
(1)AO与A'C'所成角的度数;
(2)AO与平面ABCD所成角的正切值;
(3)平面AOB与平面AOC所成二面角的大小.
21.(12分)如图所示,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
证明:(1)AA1⊥BD;
(2)CC1∥平面A1BD.
22.(12分)如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
第八章测评
(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列说法正确的是( )
A.圆锥的侧面展开图是一个等腰三角形
B.棱柱即是两个底面全等且其余各面都是矩形的多面体
C.任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
D.通过圆台侧面上一点,有无数条母线
解析:圆锥的侧面展开图是一个扇形,故A错误;由棱柱的定义知B错误;通过圆台侧面上一点,有且只有一条母线,故D错误;因为棱台是由一个大棱锥被一个平行于底面的平面所截,夹在截面与底面的部分,所以任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥,故C正确.
答案:C
2.如图所示,在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于( )
A.AC B.BD C.A1D D.A1D1
解析:CE 平面ACC1A1,
∵BD⊥AC,BD⊥AA1,AC∩AA1=A,
∴BD⊥平面ACC1A1,
∴BD⊥CE.
答案:B
3.如图,Rt△O'A'B'是一平面图形的直观图,斜边O'B'=2,则这个平面图形的面积是( )
A B.1
C D.2
解析:在直观图中,∵O'B'=2,∠A'O'B'=45°,∠O'A'B'=90°,
∴O'A'=A'B'=2
∴S△O'A'B'==1.
∴这个平面图形的面积S=2S△O'A'B'=2
故选D.
答案:D
4.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何 ”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底面的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少 ”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )(“斛”不是国际通用单位)
A.14斛 B.22斛
C.36斛 D.66斛
解析:设米堆的底面半径为r,则r=8,故r=(尺),则V米堆=r2h5(立方尺).
因为1斛米的体积约为1.62立方尺,所以堆放的米约有÷1.62≈22(斛).
答案:B
5.如图,四棱锥S-ABCD所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A.2+ B.3+
C.3+2 D.2+2
解析:∵AB=BC=CD=DA=2,
∴四边形ABCD为菱形,
∴AB∥CD,从而AB∥平面DEFC,
∵AB 平面SAB,平面SAB∩平面DEFC=EF,
∴AB∥EF.
又E是SA的中点,
∴F为SB的中点,
∴EF=1,DE=CF=
∴四边形DEFC的周长为3+2
答案:C
6.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π
C.144π D.256π
解析:本题主要考查空间几何体.
设球O的半径为R,则S△AOB=R2.
当OC⊥平面AOB时,三棱锥O-ABC的体积最大,此时V=R2·R=36,解得R=6,所以球O的表面积S=4πR2=144π.
答案:C
7.已知平面α⊥平面β,α∩β=l,在l上取线段AB=4,AC,BD分别在平面α和平面β内,且AC⊥AB,DB⊥AB,AC=3,BD=12,则CD的长度为( )
A.13 B C.12 D.15
解析:如图,连接AD.
由题意知AC⊥β,DB⊥α.
在Rt△ABD中,AD=
在Rt△CAD中,CD==13.
答案:A
8.已知平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
A B
C D
解析:如图,在正方体ABCD-A1B1C1D1的上方接一个同等大小的正方体ABCD-A2B2C2D2,则过点A与平面CB1D1平行的是平面AB2D2,即平面α就是平面AB2D2,平面AB2D2∩平面ABB1A1=AB2,即直线n就是直线AB2,易知平面ABCD∥平面A2B2C2D2,由面面平行的性质定理知直线m平行于直线B2D2,故m,n所成的角就等于AB2与B2D2所成的角,在等边三角形AB2D2中,∠AB2D2=60°,故其正弦值为故选A.
答案:A
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.用一个平面去截一个几何体,得到的截面是圆面,则这个几何体可能是( )
A.圆锥 B.圆柱
C.球 D.棱柱
解析:对于A,圆锥的底面是圆,则用一个平面去截,得到的截面可能是圆面;
对于B,圆柱的底面是圆,则用一个平面去截,得到的截面可能是圆面;
对于C,用任意的平面去截球,得到的截面均为圆面;
对于D,用任意的平面去截棱柱,得到的截面都不可能是圆面.
答案:ABC
10.已知直线l⊥平面α,直线m 平面β.则下列结论正确的是( )
A.α∥β l⊥m B.α⊥β l∥m
C.l∥m α⊥β D.l⊥m α∥β
解析:A项中,∵l⊥α,α∥β,∴l⊥β.
又m β,∴l⊥m,故A正确.
B项中,由l⊥α,α⊥β可得l∥β或l β,再由m β得不到l∥m,故B错误.
C项中,∵l⊥α,m∥l,∴m⊥α,又m β,∴α⊥β,故C正确.
D项中,若α∩β=m,也可满足l⊥α,l⊥m,故D错误.
答案:AC
11.一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,则下列结论正确的是( )
A.圆柱的侧面积为2πR2
B.圆锥的侧面积为2πR2
C.圆柱的侧面积与球的表面积相等
D.圆柱、圆锥、球的体积之比为3∶1∶2
解析:依题意得球的半径为R,则圆柱的侧面积为2πR·2R=4πR2,∴A错误;
圆锥的侧面积为πRR=R2,∴B错误;
球的表面积为4πR2,
∵圆柱的侧面积为4πR2,∴C正确;
∵V圆柱=πR2·2R=2πR3,
V圆锥=R2·2R=R3,V球=R3,
∴V圆柱∶V圆锥∶V球=2πR3R3R3=3∶1∶2,
∴D正确.故选CD.
答案:CD
12.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是 ( )
A.PB⊥AD
B.平面PAB⊥平面PBD
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
解析:∵PB在底面的射影为AB,AB与AD不垂直,
∴AD与PB不垂直,故A不正确;
又BD⊥AB,BD⊥PA,AB∩PA=A,
∴BD⊥平面PAB.
又BD 平面PBD,∴平面PBD⊥平面PAB.故B正确;
∵BD∥AE,∴BD∥平面PAE,∴BC与平面PAE不平行,故C不正确;
∵PD与平面ABC所成的角为∠PDA,且在Rt△PAD中,AD=2AB=PA,∴∠PDA=45°,故D正确.
答案:BD
三、填空题:本题共4小题,每小题5分,共20分.
13.现有用橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2,高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为 .
解析:设新的圆锥和圆柱的底面半径均为r,
则52×4+π×22×8=r2×4+πr2×8,
即r2=+32π,解得r=
答案:
14.在四面体A-BCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=,则异面直线AD与BC所成角的大小为 .
解析:如图①,取AC的中点M,连接EM,FM.
因为F为DC的中点,M为AC的中点,所以FM∥AD,且FM=AD=1.
同理EM∥BC,且EM=BC=1.
故∠EMF或其补角为异面直线AD与BC所成的角.
图①
图②
如图②,在△EMF中,作MN⊥EF于点N,则N为EF的中点.
在Rt△MNE中,EM=1,EN=,
所以sin∠EMN=,从而∠EMN=60°,∠EMF=120°.
故AD与BC所成角为60°.
答案:60°
15.已知在四面体P-ABC中,PA=PB=4,PC=2,AC=2,PB⊥平面PAC,则四面体P-ABC外接球的体积为 .
解析:∵PA=4,PC=2,AC=2,∴在△PAC中,PA2+PC2=20=AC2,可得AP⊥PC.
又PB⊥平面PAC,PA,PC 平面PAC,
∴PB⊥PA,PB⊥PC.
以PA,PC,PB分别为长、宽、高,作长方体如图所示,则该长方体的外接球就是四面体P-ABC的外接球.
∵长方体的体对角线长为=6,
∴长方体外接球的直径2R=6,则R=3.
因此,四面体P-ABC外接球的体积为V=R3=36π.
答案:36π
16.如图,P是边长为2的正方形ABCD外一点,PA⊥AB,PA⊥BC,且PC=5,则直线BD与平面PAC的位置关系为 ,二面角P-BD-A的余弦值为 .
解析:∵PA⊥AB,PA⊥BC,AB∩BC=B,
∴PA⊥平面ABCD.
又BD 平面ABCD,∴PA⊥BD.
∵四边形ABCD为正方形,∴BD⊥AC.
∵PA∩AC=A,∴BD⊥平面PAC.
如图,设AC∩BD=O,连接PO,
则BD⊥PO.
∴∠POA为二面角P-BD-A的平面角.
又AB=2,∴AC=4,∴AO=2.
∴PA==3.
∴PO=,
∴cos∠POA=
答案:垂直
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)如图,求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积(单位:cm).
解:由题意知,所求旋转体的表面积由三部分组成:圆台下底面、侧面和一半球面.
S半球=8π,S圆台侧=35π,S圆台底=25π.
故所求几何体的表面积为68πcm2.
由V圆台=(π×22++π×52)×4=52π,V半球=23,
所以所求几何体的体积为V圆台-V半球=52π-=(cm3).
18.(12分)如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合于点G,得到多面体CDEFG.
(1)求证:平面DEG⊥平面CFG;
(2)求多面体CDEFG的体积.
(1)证明:由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得EG⊥GF.
因为CF⊥EF,CF⊥GF,且EF∩GF=F,所以CF⊥平面EGF,所以可得CF⊥EG.
因为GF∩CF=F,所以EG⊥平面CFG.
又因为EG 平面DEG,
所以平面DEG⊥平面CFG.
(2)解:过点G作GO垂直于EF,垂足为O,则GO=
由(1)知CF⊥平面EGF,CF 平面CDEF,所以平面EGF⊥平面CDEF,且交线为EF.
所以GO⊥平面CDEF,即GO为四棱锥G-CDEF的高.
所以所求体积为S长方形CDEF·GO=4×5=16.
19.(12分)如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
证明:(1)在直三棱柱ABC-A1B1C1中,A1C1∥AC.
在△ABC中,因为D,E分别为AB,BC的中点,
所以DE∥AC,于是DE∥A1C1.
又因为DE 平面A1C1F,A1C1 平面A1C1F,
所以直线DE∥平面A1C1F.
(2)在直三棱柱ABC-A1B1C1中,A1A⊥平面A1B1C1,
因为A1C1 平面A1B1C1,所以A1A⊥A1C1.
又因为A1C1⊥A1B1,AA1 平面ABB1A1,A1B1 平面ABB1A1,且A1A∩A1B1=A1,
所以A1C1⊥平面ABB1A1.
因为B1D 平面ABB1A1,所以A1C1⊥B1D.
又因为B1D⊥A1F,A1C1 平面A1C1F,A1F 平面A1C1F,A1C1∩A1F=A1,所以B1D⊥平面A1C1F.
因为B1D 平面B1DE,所以平面B1DE⊥平面A1C1F.
20.(12分)如图所示,正方体的棱长为1,B'C∩BC'=O,求:
(1)AO与A'C'所成角的度数;
(2)AO与平面ABCD所成角的正切值;
(3)平面AOB与平面AOC所成二面角的大小.
解:(1)由题意得A'C'∥AC,
∴∠OAC或其补角即为AO与A'C'所成的角.
∵在正方体A'C中,AB⊥平面BC',
∴OC⊥AB.
又OC⊥OB,且AB∩OB=B,
∴OC⊥平面ABO.
∵OA 平面ABO,
∴OC⊥OA.
∵在Rt△AOC中,OC=,AC=,
∴sin∠OAC=,
∴∠OAC=30°.
即AO与A'C'所成角的度数为30°.
(2)如图所示,过点O作OE⊥BC于点E,连接AE.
∵平面BC'⊥平面ABCD,且交线为BC,
∴OE⊥平面ABCD,从而∠OAE即为AO与平面ABCD所成的角.
在Rt△OAE中,OE=,AE=,∴tan∠OAE=
即AO与平面ABCD所成角的正切值为
(3)由(1)知,OC⊥平面AOB.
又OC 平面AOC,
∴平面AOB⊥平面AOC,
即平面AOB与平面AOC所成二面角的大小为90°.
21.(12分)如图所示,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
证明:(1)AA1⊥BD;
(2)CC1∥平面A1BD.
证明:(1)∵AB=2AD,∠BAD=60°,
∴BD⊥AD.
∵D1D⊥平面ABCD,
∴D1D⊥DB.
又AD∩D1D=D,
∴BD⊥平面A1ADD1,
∴AA1⊥BD.
(2)如图,连接AC,A1C1,AC交BD于点O,连接A1O.
∵四棱台底面ABCD是平行四边形,
∴OC=AC.
由棱台定义,AB=2A1B1及平面与平面平行的性质定理得A1C1∥OC,且A1C1=OC.
∴四边形A1OCC1为平行四边形.
∴CC1∥A1O.
又A1O 平面A1BD,CC1 平面A1BD,
∴CC1∥平面A1BD.
22.(12分)如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
解:(1)在梯形ABCD中,AB与CD不平行.
如图,延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点.
理由如下:
由题意知,BC∥ED,且BC=ED,
所以四边形BCDE是平行四边形,从而CM∥EB.
又因为EB 平面PBE,CM 平面PBE,
所以CM∥平面PBE.
(2)已知CD⊥PA,CD⊥AD,PA∩AD=A,
所以CD⊥平面PAD.
因为PD 平面PAD,
所以CD⊥PD.
又因为CD⊥AD,
所以∠PDA是二面角P-CD-A的平面角,
所以∠PDA=45°.
由题意知PA⊥平面ABCD.
设BC=1,则在Rt△PAD中,PA=AD=2.
由题意知AE=ED=CD=1.
所以在Rt△PAE中,PE=,在Rt△CDE中,CE=,在Rt△PAD中,PD=2,在Rt△PDC中,PC=3.
设点A到平面PCE的距离为m,PA与平面PCE所成角为β.
连接AC,则VA-PEC=VP-AEC.①
已知△PEC的三边,根据余弦定理、三角形面积计算公式,得S△PEC=
S△AEC=AE·CD=
代入①得m=PA,已知PA=2,
解得m=,
故sinβ=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第八章测评
(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列说法正确的是( )
A.圆锥的侧面展开图是一个等腰三角形
B.棱柱即是两个底面全等且其余各面都是矩形的多面体
C.任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
D.通过圆台侧面上一点,有无数条母线
2.如图所示,在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于( )
A.AC B.BD C.A1D D.A1D1
3.如图,Rt△O'A'B'是一平面图形的直观图,斜边O'B'=2,则这个平面图形的面积是( )
A B.1
C D.2
4.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何 ”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底面的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少 ”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )(“斛”不是国际通用单位)
A.14斛 B.22斛
C.36斛 D.66斛
5.如图,四棱锥S-ABCD所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A.2+ B.3+
C.3+2 D.2+2
6.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π
C.144π D.256π
7.已知平面α⊥平面β,α∩β=l,在l上取线段AB=4,AC,BD分别在平面α和平面β内,且AC⊥AB,DB⊥AB,AC=3,BD=12,则CD的长度为( )
A.13 B C.12 D.15
8.已知平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
A B
C D
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.用一个平面去截一个几何体,得到的截面是圆面,则这个几何体可能是( )
A.圆锥 B.圆柱
C.球 D.棱柱
10.已知直线l⊥平面α,直线m 平面β.则下列结论正确的是( )
A.α∥β l⊥m B.α⊥β l∥m
C.l∥m α⊥β D.l⊥m α∥β
11.一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,则下列结论正确的是( )
A.圆柱的侧面积为2πR2
B.圆锥的侧面积为2πR2
C.圆柱的侧面积与球的表面积相等
D.圆柱、圆锥、球的体积之比为3∶1∶2
12.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是 ( )
A.PB⊥AD
B.平面PAB⊥平面PBD
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
三、填空题:本题共4小题,每小题5分,共20分.
13.现有用橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2,高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为 .
14.在四面体A-BCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=,则异面直线AD与BC所成角的大小为 .
15.已知在四面体P-ABC中,PA=PB=4,PC=2,AC=2,PB⊥平面PAC,则四面体P-ABC外接球的体积为 .
16.如图,P是边长为2的正方形ABCD外一点,PA⊥AB,PA⊥BC,且PC=5,则直线BD与平面PAC的位置关系为 ,二面角P-BD-A的余弦值为 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)如图,求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积(单位:cm).
18.(12分)如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合于点G,得到多面体CDEFG.
(1)求证:平面DEG⊥平面CFG;
(2)求多面体CDEFG的体积.
19.(12分)如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
20.(12分)如图所示,正方体的棱长为1,B'C∩BC'=O,求:
(1)AO与A'C'所成角的度数;
(2)AO与平面ABCD所成角的正切值;
(3)平面AOB与平面AOC所成二面角的大小.
21.(12分)如图所示,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
证明:(1)AA1⊥BD;
(2)CC1∥平面A1BD.
22.(12分)如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
第八章测评
(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列说法正确的是( )
A.圆锥的侧面展开图是一个等腰三角形
B.棱柱即是两个底面全等且其余各面都是矩形的多面体
C.任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
D.通过圆台侧面上一点,有无数条母线
解析:圆锥的侧面展开图是一个扇形,故A错误;由棱柱的定义知B错误;通过圆台侧面上一点,有且只有一条母线,故D错误;因为棱台是由一个大棱锥被一个平行于底面的平面所截,夹在截面与底面的部分,所以任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥,故C正确.
答案:C
2.如图所示,在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于( )
A.AC B.BD C.A1D D.A1D1
解析:CE 平面ACC1A1,
∵BD⊥AC,BD⊥AA1,AC∩AA1=A,
∴BD⊥平面ACC1A1,
∴BD⊥CE.
答案:B
3.如图,Rt△O'A'B'是一平面图形的直观图,斜边O'B'=2,则这个平面图形的面积是( )
A B.1
C D.2
解析:在直观图中,∵O'B'=2,∠A'O'B'=45°,∠O'A'B'=90°,
∴O'A'=A'B'=2
∴S△O'A'B'==1.
∴这个平面图形的面积S=2S△O'A'B'=2
故选D.
答案:D
4.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何 ”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底面的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少 ”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )(“斛”不是国际通用单位)
A.14斛 B.22斛
C.36斛 D.66斛
解析:设米堆的底面半径为r,则r=8,故r=(尺),则V米堆=r2h5(立方尺).
因为1斛米的体积约为1.62立方尺,所以堆放的米约有÷1.62≈22(斛).
答案:B
5.如图,四棱锥S-ABCD所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A.2+ B.3+
C.3+2 D.2+2
解析:∵AB=BC=CD=DA=2,
∴四边形ABCD为菱形,
∴AB∥CD,从而AB∥平面DEFC,
∵AB 平面SAB,平面SAB∩平面DEFC=EF,
∴AB∥EF.
又E是SA的中点,
∴F为SB的中点,
∴EF=1,DE=CF=
∴四边形DEFC的周长为3+2
答案:C
6.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π
C.144π D.256π
解析:本题主要考查空间几何体.
设球O的半径为R,则S△AOB=R2.
当OC⊥平面AOB时,三棱锥O-ABC的体积最大,此时V=R2·R=36,解得R=6,所以球O的表面积S=4πR2=144π.
答案:C
7.已知平面α⊥平面β,α∩β=l,在l上取线段AB=4,AC,BD分别在平面α和平面β内,且AC⊥AB,DB⊥AB,AC=3,BD=12,则CD的长度为( )
A.13 B C.12 D.15
解析:如图,连接AD.
由题意知AC⊥β,DB⊥α.
在Rt△ABD中,AD=
在Rt△CAD中,CD==13.
答案:A
8.已知平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
A B
C D
解析:如图,在正方体ABCD-A1B1C1D1的上方接一个同等大小的正方体ABCD-A2B2C2D2,则过点A与平面CB1D1平行的是平面AB2D2,即平面α就是平面AB2D2,平面AB2D2∩平面ABB1A1=AB2,即直线n就是直线AB2,易知平面ABCD∥平面A2B2C2D2,由面面平行的性质定理知直线m平行于直线B2D2,故m,n所成的角就等于AB2与B2D2所成的角,在等边三角形AB2D2中,∠AB2D2=60°,故其正弦值为故选A.
答案:A
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.用一个平面去截一个几何体,得到的截面是圆面,则这个几何体可能是( )
A.圆锥 B.圆柱
C.球 D.棱柱
解析:对于A,圆锥的底面是圆,则用一个平面去截,得到的截面可能是圆面;
对于B,圆柱的底面是圆,则用一个平面去截,得到的截面可能是圆面;
对于C,用任意的平面去截球,得到的截面均为圆面;
对于D,用任意的平面去截棱柱,得到的截面都不可能是圆面.
答案:ABC
10.已知直线l⊥平面α,直线m 平面β.则下列结论正确的是( )
A.α∥β l⊥m B.α⊥β l∥m
C.l∥m α⊥β D.l⊥m α∥β
解析:A项中,∵l⊥α,α∥β,∴l⊥β.
又m β,∴l⊥m,故A正确.
B项中,由l⊥α,α⊥β可得l∥β或l β,再由m β得不到l∥m,故B错误.
C项中,∵l⊥α,m∥l,∴m⊥α,又m β,∴α⊥β,故C正确.
D项中,若α∩β=m,也可满足l⊥α,l⊥m,故D错误.
答案:AC
11.一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,则下列结论正确的是( )
A.圆柱的侧面积为2πR2
B.圆锥的侧面积为2πR2
C.圆柱的侧面积与球的表面积相等
D.圆柱、圆锥、球的体积之比为3∶1∶2
解析:依题意得球的半径为R,则圆柱的侧面积为2πR·2R=4πR2,∴A错误;
圆锥的侧面积为πRR=R2,∴B错误;
球的表面积为4πR2,
∵圆柱的侧面积为4πR2,∴C正确;
∵V圆柱=πR2·2R=2πR3,
V圆锥=R2·2R=R3,V球=R3,
∴V圆柱∶V圆锥∶V球=2πR3R3R3=3∶1∶2,
∴D正确.故选CD.
答案:CD
12.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是 ( )
A.PB⊥AD
B.平面PAB⊥平面PBD
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
解析:∵PB在底面的射影为AB,AB与AD不垂直,
∴AD与PB不垂直,故A不正确;
又BD⊥AB,BD⊥PA,AB∩PA=A,
∴BD⊥平面PAB.
又BD 平面PBD,∴平面PBD⊥平面PAB.故B正确;
∵BD∥AE,∴BD∥平面PAE,∴BC与平面PAE不平行,故C不正确;
∵PD与平面ABC所成的角为∠PDA,且在Rt△PAD中,AD=2AB=PA,∴∠PDA=45°,故D正确.
答案:BD
三、填空题:本题共4小题,每小题5分,共20分.
13.现有用橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2,高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为 .
解析:设新的圆锥和圆柱的底面半径均为r,
则52×4+π×22×8=r2×4+πr2×8,
即r2=+32π,解得r=
答案:
14.在四面体A-BCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=,则异面直线AD与BC所成角的大小为 .
解析:如图①,取AC的中点M,连接EM,FM.
因为F为DC的中点,M为AC的中点,所以FM∥AD,且FM=AD=1.
同理EM∥BC,且EM=BC=1.
故∠EMF或其补角为异面直线AD与BC所成的角.
图①
图②
如图②,在△EMF中,作MN⊥EF于点N,则N为EF的中点.
在Rt△MNE中,EM=1,EN=,
所以sin∠EMN=,从而∠EMN=60°,∠EMF=120°.
故AD与BC所成角为60°.
答案:60°
15.已知在四面体P-ABC中,PA=PB=4,PC=2,AC=2,PB⊥平面PAC,则四面体P-ABC外接球的体积为 .
解析:∵PA=4,PC=2,AC=2,∴在△PAC中,PA2+PC2=20=AC2,可得AP⊥PC.
又PB⊥平面PAC,PA,PC 平面PAC,
∴PB⊥PA,PB⊥PC.
以PA,PC,PB分别为长、宽、高,作长方体如图所示,则该长方体的外接球就是四面体P-ABC的外接球.
∵长方体的体对角线长为=6,
∴长方体外接球的直径2R=6,则R=3.
因此,四面体P-ABC外接球的体积为V=R3=36π.
答案:36π
16.如图,P是边长为2的正方形ABCD外一点,PA⊥AB,PA⊥BC,且PC=5,则直线BD与平面PAC的位置关系为 ,二面角P-BD-A的余弦值为 .
解析:∵PA⊥AB,PA⊥BC,AB∩BC=B,
∴PA⊥平面ABCD.
又BD 平面ABCD,∴PA⊥BD.
∵四边形ABCD为正方形,∴BD⊥AC.
∵PA∩AC=A,∴BD⊥平面PAC.
如图,设AC∩BD=O,连接PO,
则BD⊥PO.
∴∠POA为二面角P-BD-A的平面角.
又AB=2,∴AC=4,∴AO=2.
∴PA==3.
∴PO=,
∴cos∠POA=
答案:垂直
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)如图,求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积(单位:cm).
解:由题意知,所求旋转体的表面积由三部分组成:圆台下底面、侧面和一半球面.
S半球=8π,S圆台侧=35π,S圆台底=25π.
故所求几何体的表面积为68πcm2.
由V圆台=(π×22++π×52)×4=52π,V半球=23,
所以所求几何体的体积为V圆台-V半球=52π-=(cm3).
18.(12分)如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合于点G,得到多面体CDEFG.
(1)求证:平面DEG⊥平面CFG;
(2)求多面体CDEFG的体积.
(1)证明:由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得EG⊥GF.
因为CF⊥EF,CF⊥GF,且EF∩GF=F,所以CF⊥平面EGF,所以可得CF⊥EG.
因为GF∩CF=F,所以EG⊥平面CFG.
又因为EG 平面DEG,
所以平面DEG⊥平面CFG.
(2)解:过点G作GO垂直于EF,垂足为O,则GO=
由(1)知CF⊥平面EGF,CF 平面CDEF,所以平面EGF⊥平面CDEF,且交线为EF.
所以GO⊥平面CDEF,即GO为四棱锥G-CDEF的高.
所以所求体积为S长方形CDEF·GO=4×5=16.
19.(12分)如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
证明:(1)在直三棱柱ABC-A1B1C1中,A1C1∥AC.
在△ABC中,因为D,E分别为AB,BC的中点,
所以DE∥AC,于是DE∥A1C1.
又因为DE 平面A1C1F,A1C1 平面A1C1F,
所以直线DE∥平面A1C1F.
(2)在直三棱柱ABC-A1B1C1中,A1A⊥平面A1B1C1,
因为A1C1 平面A1B1C1,所以A1A⊥A1C1.
又因为A1C1⊥A1B1,AA1 平面ABB1A1,A1B1 平面ABB1A1,且A1A∩A1B1=A1,
所以A1C1⊥平面ABB1A1.
因为B1D 平面ABB1A1,所以A1C1⊥B1D.
又因为B1D⊥A1F,A1C1 平面A1C1F,A1F 平面A1C1F,A1C1∩A1F=A1,所以B1D⊥平面A1C1F.
因为B1D 平面B1DE,所以平面B1DE⊥平面A1C1F.
20.(12分)如图所示,正方体的棱长为1,B'C∩BC'=O,求:
(1)AO与A'C'所成角的度数;
(2)AO与平面ABCD所成角的正切值;
(3)平面AOB与平面AOC所成二面角的大小.
解:(1)由题意得A'C'∥AC,
∴∠OAC或其补角即为AO与A'C'所成的角.
∵在正方体A'C中,AB⊥平面BC',
∴OC⊥AB.
又OC⊥OB,且AB∩OB=B,
∴OC⊥平面ABO.
∵OA 平面ABO,
∴OC⊥OA.
∵在Rt△AOC中,OC=,AC=,
∴sin∠OAC=,
∴∠OAC=30°.
即AO与A'C'所成角的度数为30°.
(2)如图所示,过点O作OE⊥BC于点E,连接AE.
∵平面BC'⊥平面ABCD,且交线为BC,
∴OE⊥平面ABCD,从而∠OAE即为AO与平面ABCD所成的角.
在Rt△OAE中,OE=,AE=,∴tan∠OAE=
即AO与平面ABCD所成角的正切值为
(3)由(1)知,OC⊥平面AOB.
又OC 平面AOC,
∴平面AOB⊥平面AOC,
即平面AOB与平面AOC所成二面角的大小为90°.
21.(12分)如图所示,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
证明:(1)AA1⊥BD;
(2)CC1∥平面A1BD.
证明:(1)∵AB=2AD,∠BAD=60°,
∴BD⊥AD.
∵D1D⊥平面ABCD,
∴D1D⊥DB.
又AD∩D1D=D,
∴BD⊥平面A1ADD1,
∴AA1⊥BD.
(2)如图,连接AC,A1C1,AC交BD于点O,连接A1O.
∵四棱台底面ABCD是平行四边形,
∴OC=AC.
由棱台定义,AB=2A1B1及平面与平面平行的性质定理得A1C1∥OC,且A1C1=OC.
∴四边形A1OCC1为平行四边形.
∴CC1∥A1O.
又A1O 平面A1BD,CC1 平面A1BD,
∴CC1∥平面A1BD.
22.(12分)如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
解:(1)在梯形ABCD中,AB与CD不平行.
如图,延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点.
理由如下:
由题意知,BC∥ED,且BC=ED,
所以四边形BCDE是平行四边形,从而CM∥EB.
又因为EB 平面PBE,CM 平面PBE,
所以CM∥平面PBE.
(2)已知CD⊥PA,CD⊥AD,PA∩AD=A,
所以CD⊥平面PAD.
因为PD 平面PAD,
所以CD⊥PD.
又因为CD⊥AD,
所以∠PDA是二面角P-CD-A的平面角,
所以∠PDA=45°.
由题意知PA⊥平面ABCD.
设BC=1,则在Rt△PAD中,PA=AD=2.
由题意知AE=ED=CD=1.
所以在Rt△PAE中,PE=,在Rt△CDE中,CE=,在Rt△PAD中,PD=2,在Rt△PDC中,PC=3.
设点A到平面PCE的距离为m,PA与平面PCE所成角为β.
连接AC,则VA-PEC=VP-AEC.①
已知△PEC的三边,根据余弦定理、三角形面积计算公式,得S△PEC=
S△AEC=AE·CD=
代入①得m=PA,已知PA=2,
解得m=,
故sinβ=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
