6.4.3余弦定理正弦定理第4课时余弦定理正弦定理应用举例课后习题新人教A版必修第二册(含解析)
文档属性
| 名称 | 6.4.3余弦定理正弦定理第4课时余弦定理正弦定理应用举例课后习题新人教A版必修第二册(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 165.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 19:34:20 | ||
图片预览



文档简介
第4课时 余弦定理、正弦定理应用举例
课后训练巩固提升
一、A组
1.已知轮船A和轮船B在中午12时离开海港C,两艘轮船航行方向的夹角为120°,轮船A的航行速度是25 n mile/h,轮船B的航行速度是15 n mile/h,下午2时两船之间的距离是( )
A.35 n mile B.35 n mile
C.35 n mile D.70 n mile
2.如图,设A,B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧的河岸边选定一点C,测出AC的距离为m,∠BAC=α,∠ACB=β,则A,B两点间的距离为( )
A B
C D
3.某人在点C测得某塔底B在南偏西80°方向,塔顶A的仰角为45°,此人沿南偏东40°方向前进10 m到D,测得塔顶A的仰角为30°,则塔高为( )
A.15 m B.5 m C.10 m D.12 m
4.如图,从热气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时热气球的高是60 m,则河流的宽度BC等于( )
A.30(+1)m B.120(-1)m
C.180(-1)m D.240(-1)m
5.如图,为测得河对岸塔AB的高,先在河岸上选一点C,使点C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高度为( )
A.10 m B.10 m C.10 m D.10 m
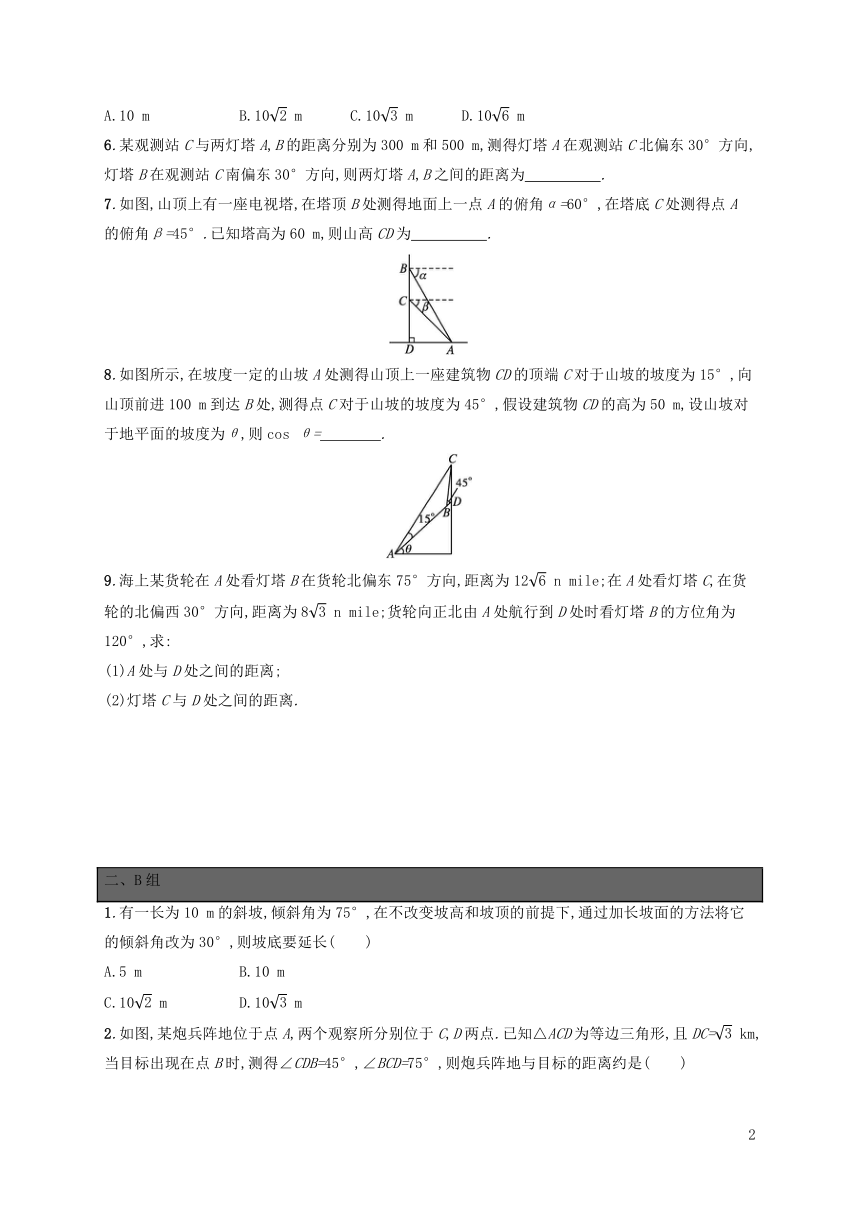
6.某观测站C与两灯塔A,B的距离分别为300 m和500 m,测得灯塔A在观测站C北偏东30°方向,灯塔B在观测站C南偏东30°方向,则两灯塔A,B之间的距离为 .
7.如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°.已知塔高为60 m,则山高CD为 .
8.如图所示,在坡度一定的山坡A处测得山顶上一座建筑物CD的顶端C对于山坡的坡度为15°,向山顶前进100 m到达B处,测得点C对于山坡的坡度为45°,假设建筑物CD的高为50 m,设山坡对于地平面的坡度为θ,则cos θ= .
9.海上某货轮在A处看灯塔B在货轮北偏东75°方向,距离为12 n mile;在A处看灯塔C,在货轮的北偏西30°方向,距离为8 n mile;货轮向正北由A处航行到D处时看灯塔B的方位角为120°,求:
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
二、B组
1.有一长为10 m的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长( )
A.5 m B.10 m
C.10 m D.10 m
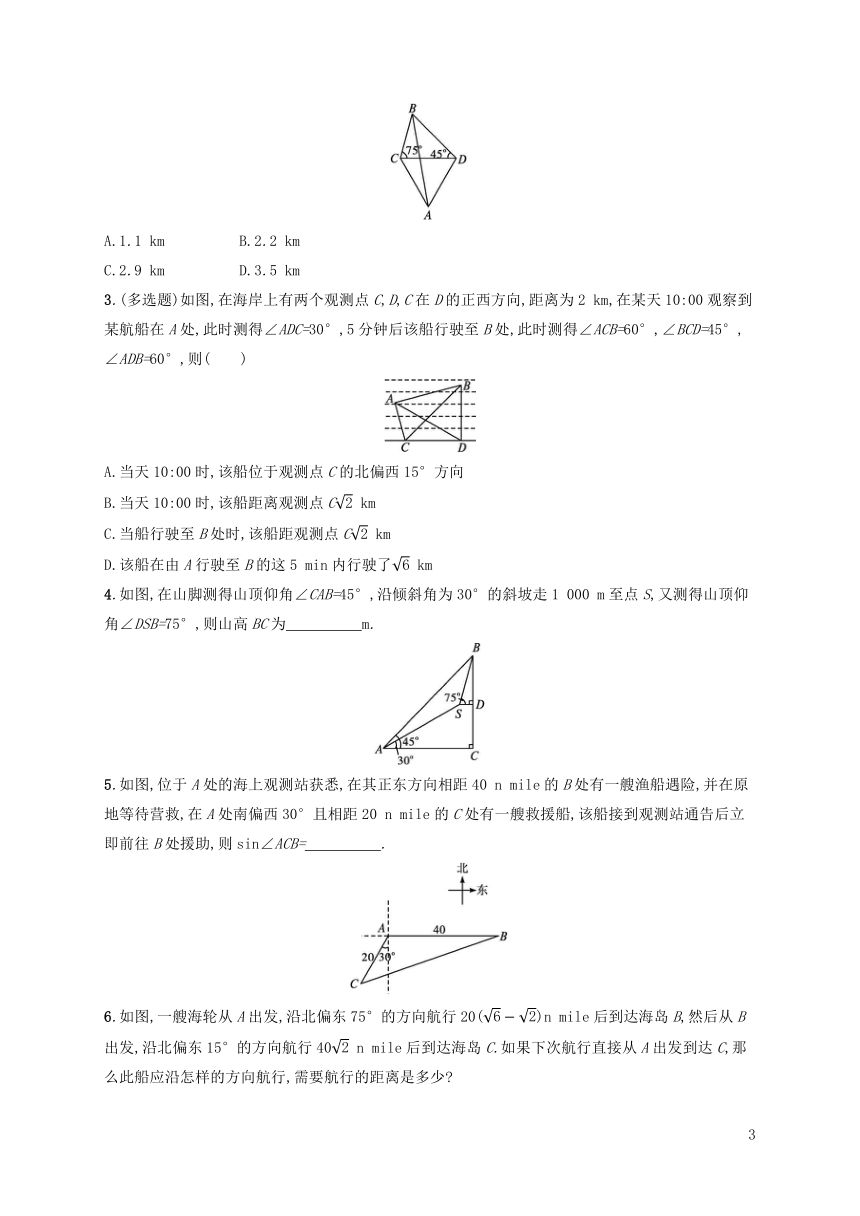
2.如图,某炮兵阵地位于点A,两个观察所分别位于C,D两点.已知△ACD为等边三角形,且DC= km,当目标出现在点B时,测得∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离约是( )
A.1.1 km B.2.2 km
C.2.9 km D.3.5 km
3.(多选题)如图,在海岸上有两个观测点C,D,C在D的正西方向,距离为2 km,在某天10:00观察到某航船在A处,此时测得∠ADC=30°,5分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则( )
A.当天10:00时,该船位于观测点C的北偏西15°方向
B.当天10:00时,该船距离观测点C km
C.当船行驶至B处时,该船距观测点C km
D.该船在由A行驶至B的这5 min内行驶了 km
4.如图,在山脚测得山顶仰角∠CAB=45°,沿倾斜角为30°的斜坡走1 000 m至点S,又测得山顶仰角∠DSB=75°,则山高BC为 m.
5.如图,位于A处的海上观测站获悉,在其正东方向相距40 n mile的B处有一艘渔船遇险,并在原地等待营救,在A处南偏西30°且相距20 n mile的C处有一艘救援船,该船接到观测站通告后立即前往B处援助,则sin∠ACB= .
6.如图,一艘海轮从A出发,沿北偏东75°的方向航行20()n mile后到达海岛B,然后从B出发,沿北偏东15°的方向航行40 n mile后到达海岛C.如果下次航行直接从A出发到达C,那么此船应沿怎样的方向航行,需要航行的距离是多少
7.如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31 km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20 km后到达D处,测得C,D两处的距离为21 km,这时此车距离A城多少千米
第4课时 余弦定理、正弦定理应用举例
课后训练巩固提升
一、A组
1.已知轮船A和轮船B在中午12时离开海港C,两艘轮船航行方向的夹角为120°,轮船A的航行速度是25 n mile/h,轮船B的航行速度是15 n mile/h,下午2时两船之间的距离是( )
A.35 n mile B.35 n mile
C.35 n mile D.70 n mile
解析:画出示意图,如图所示,由题意可知∠C=120°,AC=50,BC=30,由余弦定理,得AB2=302+502-2×50×30×=4900,得AB=70.
答案:D
2.如图,设A,B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧的河岸边选定一点C,测出AC的距离为m,∠BAC=α,∠ACB=β,则A,B两点间的距离为( )
A B
C D
解析:在△ABC中,AC=m,∠BAC=α,∠BCA=β.
则∠ABC=π-α-β.
即sin∠ABC=sin(π-α-β)=sin(α+β).
由正弦定理,得,得AB=
答案:C
3.某人在点C测得某塔底B在南偏西80°方向,塔顶A的仰角为45°,此人沿南偏东40°方向前进10 m到D,测得塔顶A的仰角为30°,则塔高为( )
A.15 m B.5 m C.10 m D.12 m
解析:如图,设塔高为hm,则AB=h,BC=h,BD=h,∠BCD=120°,CD=10,
由余弦定理,得BD2=BC2+CD2-2BC·CDcos120°,解得h=10.
答案:C
4.如图,从热气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时热气球的高是60 m,则河流的宽度BC等于( )
A.30(+1)m B.120(-1)m
C.180(-1)m D.240(-1)m
解析:由题意可知,BC=60tan60°-60tan(90°-75°)=60()=60()=120(-1)(m).
答案:B
5.如图,为测得河对岸塔AB的高,先在河岸上选一点C,使点C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高度为( )
A.10 m B.10 m C.10 m D.10 m
解析:依题意,在△BCD中,CD=10m,∠BCD=105°,∠BDC=45°,则∠DBC=180°-45°-105°=30°,
由正弦定理,得,得BC==10(m).
在Rt△ABC中,∠BCA=60°,
即AB=BCtan∠BCA=10=10(m).
故塔AB的高度为10m.
答案:D
6.某观测站C与两灯塔A,B的距离分别为300 m和500 m,测得灯塔A在观测站C北偏东30°方向,灯塔B在观测站C南偏东30°方向,则两灯塔A,B之间的距离为 .
解析:如图所示,在△ABC中,AC=300m,BC=500m,∠ACB=120°.
由余弦定理,
得AB===700(m).
答案:700 m
7.如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°.已知塔高为60 m,则山高CD为 .
解析:在△ABC中,BC=60m,∠BAC=15°,∠ABC=30°.
由正弦定理,得AC==30()(m),
即CD=ACsin45°=30(+1)(m).
答案:30(+1)m
8.如图所示,在坡度一定的山坡A处测得山顶上一座建筑物CD的顶端C对于山坡的坡度为15°,向山顶前进100 m到达B处,测得点C对于山坡的坡度为45°,假设建筑物CD的高为50 m,设山坡对于地平面的坡度为θ,则cos θ= .
解析:在△ABC中,AB=100,∠CAB=15°,∠ACB=45°-15°=30°.
由正弦定理,得,故BC=200sin15°.
在△DBC中,CD=50,∠CBD=45°,∠CDB=90°+θ.
由正弦定理,得,
故cosθ=-1.
答案:-1
9.海上某货轮在A处看灯塔B在货轮北偏东75°方向,距离为12 n mile;在A处看灯塔C,在货轮的北偏西30°方向,距离为8 n mile;货轮向正北由A处航行到D处时看灯塔B的方位角为120°,求:
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
解:由题意画出示意图.
(1)在△ABD中,由已知得∠ADB=60°,B=45°,AB=12nmile.
由正弦定理,得AD==24(nmile).
(2)在△ADC中,由余弦定理,得CD2=AD2+AC2-2AD·ACcos30°=242+(8)2-2×24×8=192,故CD=8(nmile).
二、B组
1.有一长为10 m的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长( )
A.5 m B.10 m
C.10 m D.10 m
解析:如图,设将坡底加长到B'时,倾斜角为30°,
在△ABB'中,∠B'=30°,∠BAB'=75°-30°=45°,AB=10m.
在△ABB'中,由正弦定理,
得BB'==10(m).
故坡底延长10m时,斜坡的倾斜角将变为30°.
答案:C
2.如图,某炮兵阵地位于点A,两个观察所分别位于C,D两点.已知△ACD为等边三角形,且DC= km,当目标出现在点B时,测得∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离约是( )
A.1.1 km B.2.2 km
C.2.9 km D.3.5 km
解析:∠CBD=180°-∠BCD-∠CDB=60°.
在△BCD中,由正弦定理,得BD=
在△ABD中,∠ADB=45°+60°=105°.
由余弦定理,得AB2=AD2+BD2-2AD·BDcos105°=3++2=5+2
则AB=2.9(km).
故炮兵阵地与目标的距离约是2.9km.
答案:C
3.(多选题)如图,在海岸上有两个观测点C,D,C在D的正西方向,距离为2 km,在某天10:00观察到某航船在A处,此时测得∠ADC=30°,5分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则( )
A.当天10:00时,该船位于观测点C的北偏西15°方向
B.当天10:00时,该船距离观测点C km
C.当船行驶至B处时,该船距观测点C km
D.该船在由A行驶至B的这5 min内行驶了 km
解析:A项中,∠ACD=∠ACB+∠BCD=60°+45°=105°,因为C在D的正西方向,所以A在C的北偏西15°方向,故A正确.
B项中,在△ACD中,∠ACD=105°,∠ADC=30°,
则∠CAD=45°.
由正弦定理,得AC=,
故B正确.
C项中,在△BCD中,∠BCD=45°,∠CDB=∠ADC+∠ADB=30°+60°=90°,即∠CBD=45°,
则BD=CD=2,于是BC=2,故C不正确.
D项中,在△ABC中,由余弦定理,得AB2=AC2+BC2-2AC·BCcos∠ACB=2+8-22=6,
即AB=km,故D正确.
答案:ABD
4.如图,在山脚测得山顶仰角∠CAB=45°,沿倾斜角为30°的斜坡走1 000 m至点S,又测得山顶仰角∠DSB=75°,则山高BC为 m.
解析:由题意得∠SAB=45°-30°=15°,∠ABS=45°-(90°-∠DSB)=30°,又AS=1000,
由正弦定理,可得,
即BS=2000sin15°,
则BD=BSsin75°=2000sin15°cos15°=1000sin30°=500(m),且DC=1000sin30°=500(m).
从而BC=DC+BD=1000(m).
答案:1 000
5.如图,位于A处的海上观测站获悉,在其正东方向相距40 n mile的B处有一艘渔船遇险,并在原地等待营救,在A处南偏西30°且相距20 n mile的C处有一艘救援船,该船接到观测站通告后立即前往B处援助,则sin∠ACB= .
解析:在△ABC中,AB=40,AC=20,∠BAC=120°.
由余弦定理,得BC2=AB2+AC2-2AB·AC·cos120°=2800,
得BC=20
由正弦定理,得sin∠ACB=
答案:
6.如图,一艘海轮从A出发,沿北偏东75°的方向航行20()n mile后到达海岛B,然后从B出发,沿北偏东15°的方向航行40 n mile后到达海岛C.如果下次航行直接从A出发到达C,那么此船应沿怎样的方向航行,需要航行的距离是多少
解:在△ABC中,AB=20(),
BC=40,∠ABC=180°-75°+15°=120°.
由余弦定理可得
AC===40
由正弦定理,得,得
sin∠BAC=
即∠BAC=45°,75°-∠BAC=30°.
故此船应沿北偏东30°方向航行,需要航行40nmile.
7.如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31 km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20 km后到达D处,测得C,D两处的距离为21 km,这时此车距离A城多少千米
解:在△BCD中,BC=31,BD=20,CD=21,由余弦定理,得cos∠BDC==-,
即cos∠ADC=,sin∠ADC=
在△ACD中,由条件知CD=21,A=60°,
则sin∠ACD=sin(60°+∠ADC)=
由正弦定理,得,解得AD==15.故这时此车距离A城15km.
1
课后训练巩固提升
一、A组
1.已知轮船A和轮船B在中午12时离开海港C,两艘轮船航行方向的夹角为120°,轮船A的航行速度是25 n mile/h,轮船B的航行速度是15 n mile/h,下午2时两船之间的距离是( )
A.35 n mile B.35 n mile
C.35 n mile D.70 n mile
2.如图,设A,B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧的河岸边选定一点C,测出AC的距离为m,∠BAC=α,∠ACB=β,则A,B两点间的距离为( )
A B
C D
3.某人在点C测得某塔底B在南偏西80°方向,塔顶A的仰角为45°,此人沿南偏东40°方向前进10 m到D,测得塔顶A的仰角为30°,则塔高为( )
A.15 m B.5 m C.10 m D.12 m
4.如图,从热气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时热气球的高是60 m,则河流的宽度BC等于( )
A.30(+1)m B.120(-1)m
C.180(-1)m D.240(-1)m
5.如图,为测得河对岸塔AB的高,先在河岸上选一点C,使点C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高度为( )
A.10 m B.10 m C.10 m D.10 m
6.某观测站C与两灯塔A,B的距离分别为300 m和500 m,测得灯塔A在观测站C北偏东30°方向,灯塔B在观测站C南偏东30°方向,则两灯塔A,B之间的距离为 .
7.如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°.已知塔高为60 m,则山高CD为 .
8.如图所示,在坡度一定的山坡A处测得山顶上一座建筑物CD的顶端C对于山坡的坡度为15°,向山顶前进100 m到达B处,测得点C对于山坡的坡度为45°,假设建筑物CD的高为50 m,设山坡对于地平面的坡度为θ,则cos θ= .
9.海上某货轮在A处看灯塔B在货轮北偏东75°方向,距离为12 n mile;在A处看灯塔C,在货轮的北偏西30°方向,距离为8 n mile;货轮向正北由A处航行到D处时看灯塔B的方位角为120°,求:
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
二、B组
1.有一长为10 m的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长( )
A.5 m B.10 m
C.10 m D.10 m
2.如图,某炮兵阵地位于点A,两个观察所分别位于C,D两点.已知△ACD为等边三角形,且DC= km,当目标出现在点B时,测得∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离约是( )
A.1.1 km B.2.2 km
C.2.9 km D.3.5 km
3.(多选题)如图,在海岸上有两个观测点C,D,C在D的正西方向,距离为2 km,在某天10:00观察到某航船在A处,此时测得∠ADC=30°,5分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则( )
A.当天10:00时,该船位于观测点C的北偏西15°方向
B.当天10:00时,该船距离观测点C km
C.当船行驶至B处时,该船距观测点C km
D.该船在由A行驶至B的这5 min内行驶了 km
4.如图,在山脚测得山顶仰角∠CAB=45°,沿倾斜角为30°的斜坡走1 000 m至点S,又测得山顶仰角∠DSB=75°,则山高BC为 m.
5.如图,位于A处的海上观测站获悉,在其正东方向相距40 n mile的B处有一艘渔船遇险,并在原地等待营救,在A处南偏西30°且相距20 n mile的C处有一艘救援船,该船接到观测站通告后立即前往B处援助,则sin∠ACB= .
6.如图,一艘海轮从A出发,沿北偏东75°的方向航行20()n mile后到达海岛B,然后从B出发,沿北偏东15°的方向航行40 n mile后到达海岛C.如果下次航行直接从A出发到达C,那么此船应沿怎样的方向航行,需要航行的距离是多少
7.如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31 km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20 km后到达D处,测得C,D两处的距离为21 km,这时此车距离A城多少千米
第4课时 余弦定理、正弦定理应用举例
课后训练巩固提升
一、A组
1.已知轮船A和轮船B在中午12时离开海港C,两艘轮船航行方向的夹角为120°,轮船A的航行速度是25 n mile/h,轮船B的航行速度是15 n mile/h,下午2时两船之间的距离是( )
A.35 n mile B.35 n mile
C.35 n mile D.70 n mile
解析:画出示意图,如图所示,由题意可知∠C=120°,AC=50,BC=30,由余弦定理,得AB2=302+502-2×50×30×=4900,得AB=70.
答案:D
2.如图,设A,B两点在河的两岸,要测量两点之间的距离,测量者在A的同侧的河岸边选定一点C,测出AC的距离为m,∠BAC=α,∠ACB=β,则A,B两点间的距离为( )
A B
C D
解析:在△ABC中,AC=m,∠BAC=α,∠BCA=β.
则∠ABC=π-α-β.
即sin∠ABC=sin(π-α-β)=sin(α+β).
由正弦定理,得,得AB=
答案:C
3.某人在点C测得某塔底B在南偏西80°方向,塔顶A的仰角为45°,此人沿南偏东40°方向前进10 m到D,测得塔顶A的仰角为30°,则塔高为( )
A.15 m B.5 m C.10 m D.12 m
解析:如图,设塔高为hm,则AB=h,BC=h,BD=h,∠BCD=120°,CD=10,
由余弦定理,得BD2=BC2+CD2-2BC·CDcos120°,解得h=10.
答案:C
4.如图,从热气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时热气球的高是60 m,则河流的宽度BC等于( )
A.30(+1)m B.120(-1)m
C.180(-1)m D.240(-1)m
解析:由题意可知,BC=60tan60°-60tan(90°-75°)=60()=60()=120(-1)(m).
答案:B
5.如图,为测得河对岸塔AB的高,先在河岸上选一点C,使点C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高度为( )
A.10 m B.10 m C.10 m D.10 m
解析:依题意,在△BCD中,CD=10m,∠BCD=105°,∠BDC=45°,则∠DBC=180°-45°-105°=30°,
由正弦定理,得,得BC==10(m).
在Rt△ABC中,∠BCA=60°,
即AB=BCtan∠BCA=10=10(m).
故塔AB的高度为10m.
答案:D
6.某观测站C与两灯塔A,B的距离分别为300 m和500 m,测得灯塔A在观测站C北偏东30°方向,灯塔B在观测站C南偏东30°方向,则两灯塔A,B之间的距离为 .
解析:如图所示,在△ABC中,AC=300m,BC=500m,∠ACB=120°.
由余弦定理,
得AB===700(m).
答案:700 m
7.如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°.已知塔高为60 m,则山高CD为 .
解析:在△ABC中,BC=60m,∠BAC=15°,∠ABC=30°.
由正弦定理,得AC==30()(m),
即CD=ACsin45°=30(+1)(m).
答案:30(+1)m
8.如图所示,在坡度一定的山坡A处测得山顶上一座建筑物CD的顶端C对于山坡的坡度为15°,向山顶前进100 m到达B处,测得点C对于山坡的坡度为45°,假设建筑物CD的高为50 m,设山坡对于地平面的坡度为θ,则cos θ= .
解析:在△ABC中,AB=100,∠CAB=15°,∠ACB=45°-15°=30°.
由正弦定理,得,故BC=200sin15°.
在△DBC中,CD=50,∠CBD=45°,∠CDB=90°+θ.
由正弦定理,得,
故cosθ=-1.
答案:-1
9.海上某货轮在A处看灯塔B在货轮北偏东75°方向,距离为12 n mile;在A处看灯塔C,在货轮的北偏西30°方向,距离为8 n mile;货轮向正北由A处航行到D处时看灯塔B的方位角为120°,求:
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
解:由题意画出示意图.
(1)在△ABD中,由已知得∠ADB=60°,B=45°,AB=12nmile.
由正弦定理,得AD==24(nmile).
(2)在△ADC中,由余弦定理,得CD2=AD2+AC2-2AD·ACcos30°=242+(8)2-2×24×8=192,故CD=8(nmile).
二、B组
1.有一长为10 m的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长( )
A.5 m B.10 m
C.10 m D.10 m
解析:如图,设将坡底加长到B'时,倾斜角为30°,
在△ABB'中,∠B'=30°,∠BAB'=75°-30°=45°,AB=10m.
在△ABB'中,由正弦定理,
得BB'==10(m).
故坡底延长10m时,斜坡的倾斜角将变为30°.
答案:C
2.如图,某炮兵阵地位于点A,两个观察所分别位于C,D两点.已知△ACD为等边三角形,且DC= km,当目标出现在点B时,测得∠CDB=45°,∠BCD=75°,则炮兵阵地与目标的距离约是( )
A.1.1 km B.2.2 km
C.2.9 km D.3.5 km
解析:∠CBD=180°-∠BCD-∠CDB=60°.
在△BCD中,由正弦定理,得BD=
在△ABD中,∠ADB=45°+60°=105°.
由余弦定理,得AB2=AD2+BD2-2AD·BDcos105°=3++2=5+2
则AB=2.9(km).
故炮兵阵地与目标的距离约是2.9km.
答案:C
3.(多选题)如图,在海岸上有两个观测点C,D,C在D的正西方向,距离为2 km,在某天10:00观察到某航船在A处,此时测得∠ADC=30°,5分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则( )
A.当天10:00时,该船位于观测点C的北偏西15°方向
B.当天10:00时,该船距离观测点C km
C.当船行驶至B处时,该船距观测点C km
D.该船在由A行驶至B的这5 min内行驶了 km
解析:A项中,∠ACD=∠ACB+∠BCD=60°+45°=105°,因为C在D的正西方向,所以A在C的北偏西15°方向,故A正确.
B项中,在△ACD中,∠ACD=105°,∠ADC=30°,
则∠CAD=45°.
由正弦定理,得AC=,
故B正确.
C项中,在△BCD中,∠BCD=45°,∠CDB=∠ADC+∠ADB=30°+60°=90°,即∠CBD=45°,
则BD=CD=2,于是BC=2,故C不正确.
D项中,在△ABC中,由余弦定理,得AB2=AC2+BC2-2AC·BCcos∠ACB=2+8-22=6,
即AB=km,故D正确.
答案:ABD
4.如图,在山脚测得山顶仰角∠CAB=45°,沿倾斜角为30°的斜坡走1 000 m至点S,又测得山顶仰角∠DSB=75°,则山高BC为 m.
解析:由题意得∠SAB=45°-30°=15°,∠ABS=45°-(90°-∠DSB)=30°,又AS=1000,
由正弦定理,可得,
即BS=2000sin15°,
则BD=BSsin75°=2000sin15°cos15°=1000sin30°=500(m),且DC=1000sin30°=500(m).
从而BC=DC+BD=1000(m).
答案:1 000
5.如图,位于A处的海上观测站获悉,在其正东方向相距40 n mile的B处有一艘渔船遇险,并在原地等待营救,在A处南偏西30°且相距20 n mile的C处有一艘救援船,该船接到观测站通告后立即前往B处援助,则sin∠ACB= .
解析:在△ABC中,AB=40,AC=20,∠BAC=120°.
由余弦定理,得BC2=AB2+AC2-2AB·AC·cos120°=2800,
得BC=20
由正弦定理,得sin∠ACB=
答案:
6.如图,一艘海轮从A出发,沿北偏东75°的方向航行20()n mile后到达海岛B,然后从B出发,沿北偏东15°的方向航行40 n mile后到达海岛C.如果下次航行直接从A出发到达C,那么此船应沿怎样的方向航行,需要航行的距离是多少
解:在△ABC中,AB=20(),
BC=40,∠ABC=180°-75°+15°=120°.
由余弦定理可得
AC===40
由正弦定理,得,得
sin∠BAC=
即∠BAC=45°,75°-∠BAC=30°.
故此船应沿北偏东30°方向航行,需要航行40nmile.
7.如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31 km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20 km后到达D处,测得C,D两处的距离为21 km,这时此车距离A城多少千米
解:在△BCD中,BC=31,BD=20,CD=21,由余弦定理,得cos∠BDC==-,
即cos∠ADC=,sin∠ADC=
在△ACD中,由条件知CD=21,A=60°,
则sin∠ACD=sin(60°+∠ADC)=
由正弦定理,得,解得AD==15.故这时此车距离A城15km.
1
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
