九年级数学上册试题 6.3反比例函数的应用-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 6.3反比例函数的应用-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 422.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-27 15:08:43 | ||
图片预览


文档简介
6.3反比例函数的应用
一、选择题
1.在公式ρ=中,当质量m一定时,密度与体积V之间的函数关系可用图象表示为( )
A. B. C. D.
2.已知电灯电路两端的电压U、灯泡内钨丝的电阻R与通过的电流I的关系式是U=IR.当U为定值时,下面说法正确的是( )
A.I与R成正比例 B.I与R成反比例
C.U与R成反比例 D.U与R成正比例
3.一次函数y=ax+b与反比例函数的图象如图所示,则( )
A.a>0,b>0,c>0 B.a<0,b<0,c<0
C.a<0,b>0,c>0 D.a<0,b<0,c>0
4.已知:正比例函数的图象与反比例函数的图象交于点轴于点如图,若的面积等于2,则( )
A. B.
C. D.
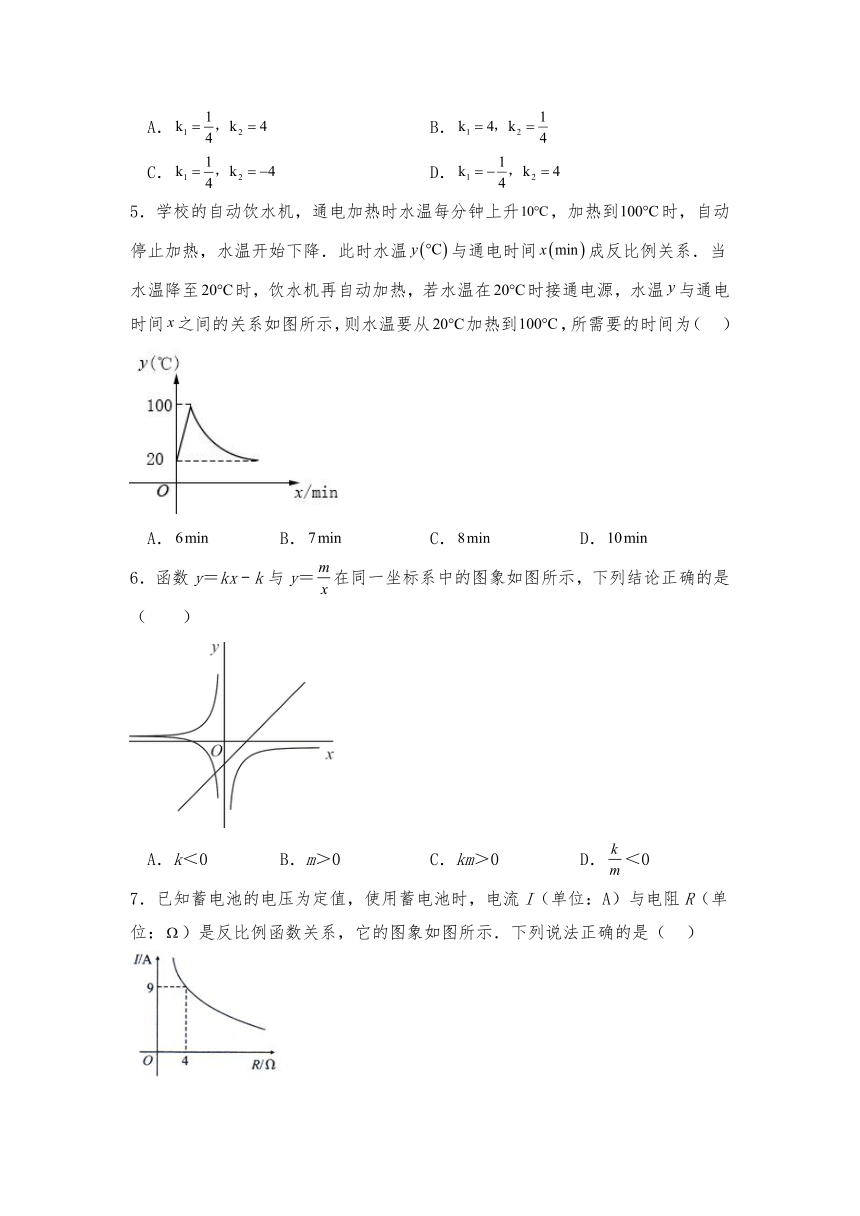
5.学校的自动饮水机,通电加热时水温每分钟上升,加热到时,自动停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则水温要从加热到,所需要的时间为( )
A. B. C. D.
6.函数y=kx﹣k与y=在同一坐标系中的图象如图所示,下列结论正确的是( )
A.k<0 B.m>0 C.km>0 D.<0
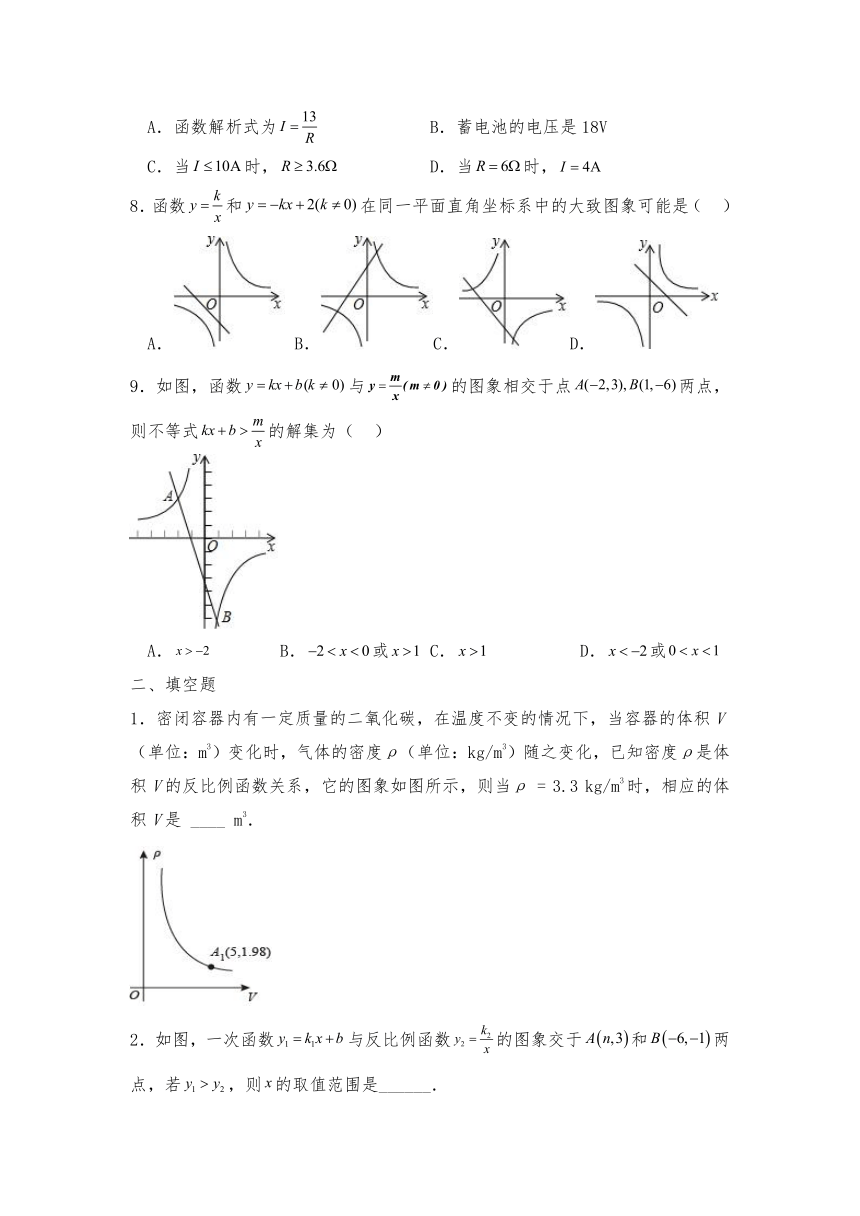
7.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
8.函数和在同一平面直角坐标系中的大致图象可能是( )
A. B.C.D.
9.如图,函数与的图象相交于点两点,则不等式的解集为( )
A. B.或 C. D.或
二、填空题
1.密闭容器内有一定质量的二氧化碳,在温度不变的情况下,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ是体积V的反比例函数关系,它的图象如图所示,则当ρ = 3.3 kg/m3时,相应的体积V是 ____ m3.
2.如图,一次函数与反比例函数的图象交于和两点,若,则的取值范围是______.
3.由电学欧姆定律知,电压不变时,电流强度I与电阻R成反比例,已知电压不变,电阻时,电流强度.则
(1)电压______V;(2)I与R的函数关系式为____________;
(3)当时的电流强度________A;
(4)当时,电阻_________.
4.已知一次函数与反比例函数的图象交于点,则________.
5.如图,在RtΔAOB中,点A是直线y=x+m与双曲线y=在第一象限的交点,且SΔAOB=2,则m的值是______.
6.如图,若反比例函数与一次函数交于、两点,当时,则的取值范围是_________.
7.如图,一块长方体大理石板的、、三个面上的边长如图所示,如果大理石板的面向下放在地上时地面所受压强为帕,则把大理石板面向下放在地上时,地面所受压强是________帕.
8.如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,与反比例函数的图象在第一象限交于点C,若,则k的值为______.
三、解答题
1.“聚能”电厂现在有5000吨煤.
(1)求:这些煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批煤能用多少天?
(3)若该电厂前10天每天用煤200吨,后因各地用电紧张,每天用煤300吨,则这批煤共可用多少天?
2.如图,在平面直角坐标系中,正比例函数与函数的图象相交于点,轴于点B.平移直线,使其经过点B,得到直线l,求直线l所对应的函数表达式.
3.如图,已知双曲线与直线交于点和点
(1)求双曲线的解析式;
(2)直接写出不等式的解集
4.密闭容器内有一定质量的气体,当容器的体积(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积是反比例函数关系,它的图像如图所示.
(1)求密度关于体积的函数解析式;
(2)当时,求该气体的密度.
5.为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?
【中小学教辅资源店 微信:mlxt2022】
答案
一、选择题
B.B.A.A.C.D.C.D.D.
二、填空题
1.3.
2.-6<x<0或x>2.
3. ; ; ; .
4.9.
5.4.
6.,.
7.3.
8.2.
三、解答题
1.(1)
由题意可得:y=.
(2)
把x=200代入y=,
得y=25.
故这批电煤能用25天.
(3)
前10天后还剩下5000-10×200=3000(吨)电煤,可以用=10(天),故共可用20天.
2.解:将代入中,,∴
∵轴于点B,.
将代入中,,解得
∴设直线l所对应的函数表达式为.
将代入上式,得 ,解得.
∴直线l所对应的函数表达式是.
故答案为.
3.解:(1)∵双曲线经过点,.
∴双曲线的解析式为
(2)由双曲线解析式可得出B(-4,-1),结合图象可得出,
不等式的解集是:或.
4.(1)
设密度关于体积的函数解析式为,
把点A的坐标代入上式中得:,
解得:k=10,
∴.
(2)
当时,().
即此时该气体的密度为1.
5.(1)设y与x的函数关系式为:y=(k≠0),
把P(144,0.5),代入得:0.5=,
解得:k=72,
∴y与x的函数解析式为:y=;
(2)当x=180时,y==0.4(万元),
答:则每月应还款0.4万元.
一、选择题
1.在公式ρ=中,当质量m一定时,密度与体积V之间的函数关系可用图象表示为( )
A. B. C. D.
2.已知电灯电路两端的电压U、灯泡内钨丝的电阻R与通过的电流I的关系式是U=IR.当U为定值时,下面说法正确的是( )
A.I与R成正比例 B.I与R成反比例
C.U与R成反比例 D.U与R成正比例
3.一次函数y=ax+b与反比例函数的图象如图所示,则( )
A.a>0,b>0,c>0 B.a<0,b<0,c<0
C.a<0,b>0,c>0 D.a<0,b<0,c>0
4.已知:正比例函数的图象与反比例函数的图象交于点轴于点如图,若的面积等于2,则( )
A. B.
C. D.
5.学校的自动饮水机,通电加热时水温每分钟上升,加热到时,自动停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则水温要从加热到,所需要的时间为( )
A. B. C. D.
6.函数y=kx﹣k与y=在同一坐标系中的图象如图所示,下列结论正确的是( )
A.k<0 B.m>0 C.km>0 D.<0
7.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
8.函数和在同一平面直角坐标系中的大致图象可能是( )
A. B.C.D.
9.如图,函数与的图象相交于点两点,则不等式的解集为( )
A. B.或 C. D.或
二、填空题
1.密闭容器内有一定质量的二氧化碳,在温度不变的情况下,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ是体积V的反比例函数关系,它的图象如图所示,则当ρ = 3.3 kg/m3时,相应的体积V是 ____ m3.
2.如图,一次函数与反比例函数的图象交于和两点,若,则的取值范围是______.
3.由电学欧姆定律知,电压不变时,电流强度I与电阻R成反比例,已知电压不变,电阻时,电流强度.则
(1)电压______V;(2)I与R的函数关系式为____________;
(3)当时的电流强度________A;
(4)当时,电阻_________.
4.已知一次函数与反比例函数的图象交于点,则________.
5.如图,在RtΔAOB中,点A是直线y=x+m与双曲线y=在第一象限的交点,且SΔAOB=2,则m的值是______.
6.如图,若反比例函数与一次函数交于、两点,当时,则的取值范围是_________.
7.如图,一块长方体大理石板的、、三个面上的边长如图所示,如果大理石板的面向下放在地上时地面所受压强为帕,则把大理石板面向下放在地上时,地面所受压强是________帕.
8.如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,与反比例函数的图象在第一象限交于点C,若,则k的值为______.
三、解答题
1.“聚能”电厂现在有5000吨煤.
(1)求:这些煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批煤能用多少天?
(3)若该电厂前10天每天用煤200吨,后因各地用电紧张,每天用煤300吨,则这批煤共可用多少天?
2.如图,在平面直角坐标系中,正比例函数与函数的图象相交于点,轴于点B.平移直线,使其经过点B,得到直线l,求直线l所对应的函数表达式.
3.如图,已知双曲线与直线交于点和点
(1)求双曲线的解析式;
(2)直接写出不等式的解集
4.密闭容器内有一定质量的气体,当容器的体积(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积是反比例函数关系,它的图像如图所示.
(1)求密度关于体积的函数解析式;
(2)当时,求该气体的密度.
5.为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?
【中小学教辅资源店 微信:mlxt2022】
答案
一、选择题
B.B.A.A.C.D.C.D.D.
二、填空题
1.3.
2.-6<x<0或x>2.
3. ; ; ; .
4.9.
5.4.
6.,.
7.3.
8.2.
三、解答题
1.(1)
由题意可得:y=.
(2)
把x=200代入y=,
得y=25.
故这批电煤能用25天.
(3)
前10天后还剩下5000-10×200=3000(吨)电煤,可以用=10(天),故共可用20天.
2.解:将代入中,,∴
∵轴于点B,.
将代入中,,解得
∴设直线l所对应的函数表达式为.
将代入上式,得 ,解得.
∴直线l所对应的函数表达式是.
故答案为.
3.解:(1)∵双曲线经过点,.
∴双曲线的解析式为
(2)由双曲线解析式可得出B(-4,-1),结合图象可得出,
不等式的解集是:或.
4.(1)
设密度关于体积的函数解析式为,
把点A的坐标代入上式中得:,
解得:k=10,
∴.
(2)
当时,().
即此时该气体的密度为1.
5.(1)设y与x的函数关系式为:y=(k≠0),
把P(144,0.5),代入得:0.5=,
解得:k=72,
∴y与x的函数解析式为:y=;
(2)当x=180时,y==0.4(万元),
答:则每月应还款0.4万元.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
