九年级数学上册试题 第四章《图形的相似》单元测试卷 -北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 第四章《图形的相似》单元测试卷 -北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-27 15:12:20 | ||
图片预览


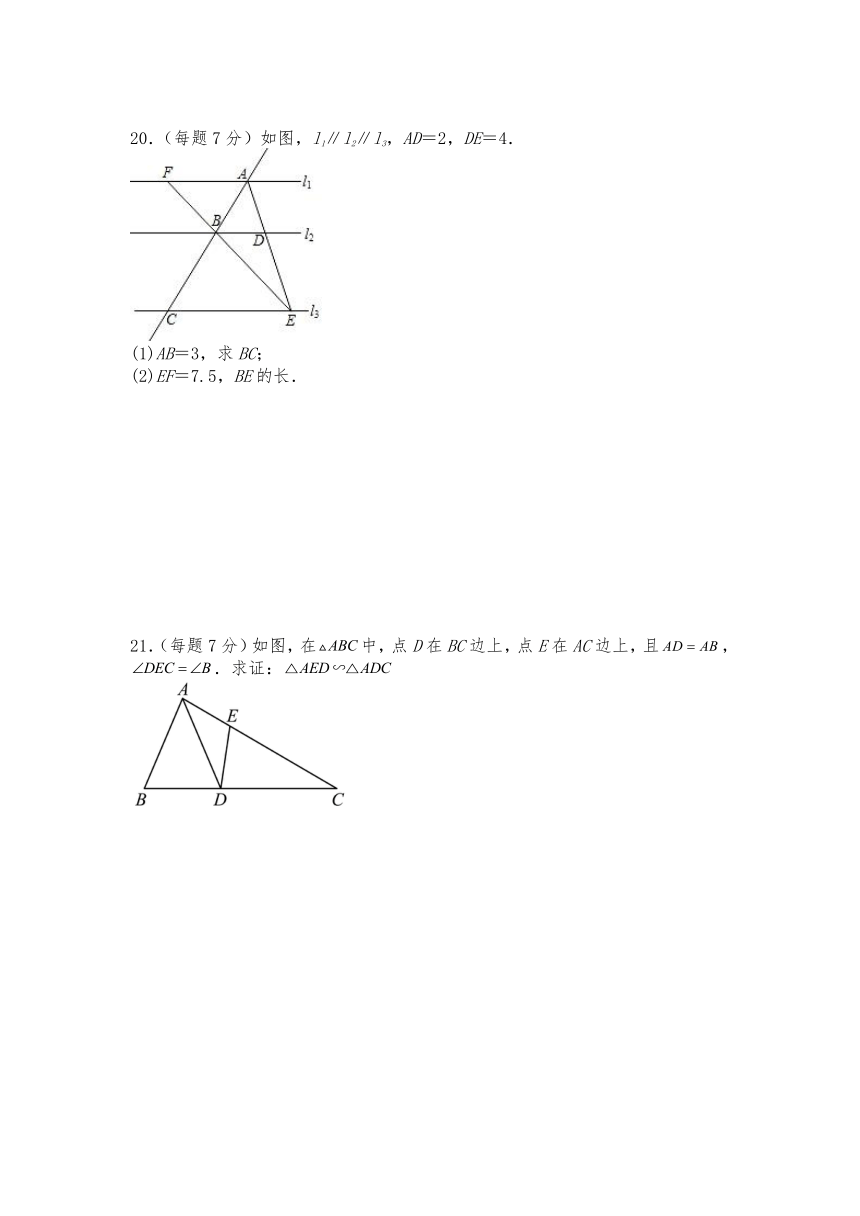
文档简介
第四章《图形的相似》单元测试卷
一、单选题(每题3分)
1.已知=5,则的值是( )
A. B.﹣ C. D.
2.已知点C是线段AB的黄金分割点,且,若AB=2,则BC=( )
A. B. C.-1 D.
3.如图,AD∥BE∥CF,AB=3,BC=2,DE=3.6,则EF的值为( )
A.1.8 B.2.4 C.4.8 D.5.4
4.已知一个三角形的三边长分别为2,3,4,与其相似的另一个三角形的周长为36,则它的最长边的长为( )
A.8 B.12 C.16 D.20
5.如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
A.4.5米 B.6米 C.3米 D.4米
6.如图所示,给出下列条件:①;②;③;④,其中单独能够判定的个数为( )
A. B. C. D.
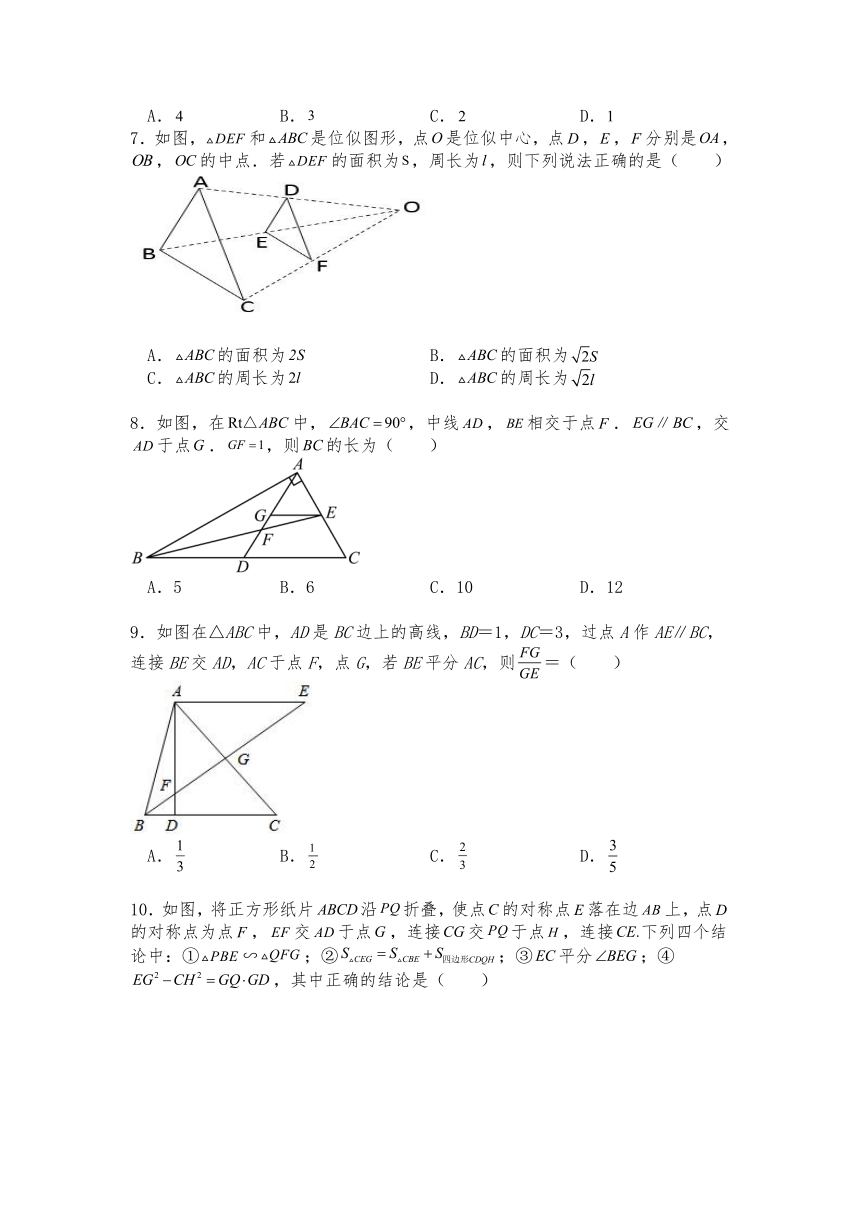
7.如图,和是位似图形,点是位似中心,点,,分别是,,的中点.若的面积为,周长为,则下列说法正确的是( )
A.的面积为 B.的面积为
C.的周长为 D.的周长为
8.如图,在中,,中线,相交于点.,交于点.,则的长为( )
A.5 B.6 C.10 D.12
9.如图在△ABC中,AD是BC边上的高线,BD=1,DC=3,过点A作AE∥BC,连接BE交AD,AC于点F,点G,若BE平分AC,则=( )
A. B. C. D.
10.如图,将正方形纸片沿折叠,使点的对称点落在边上,点的对称点为点,交于点,连接交于点,连接下列四个结论中:①∽;②;③平分;④,其中正确的结论是( )
A.①② B.①②③ C.①③④ D.②③④
二、填空题(每题3分)
11.在比例尺为的某市旅游地图上,某条道路的长为,则这条道路的实际长度为______.
12.已知线段,点是线段的黄金分割点,且,则____.
13.已知,如图,在中,,且.若,则__________,__________.
14.如图,在与中,,,,交于点D,给出下列结论.①;②;③;④.其中正确的结论是__________(填写正确结论的序号).
15.如图所示,诗的意思是:有正方形的城池一座,四面城墙的正中有门,从南门口(点D)直行8里有一塔(点A),自西门(点E)直行2里至点B,切城角(点C)也可以看见塔,问这座方城每面城墙的长是_________里.
16.如图,在平面直角坐标系中,与是位似图形,坐标原点O为位似中心.A与,B与是对应顶点.已知,则的长为________.
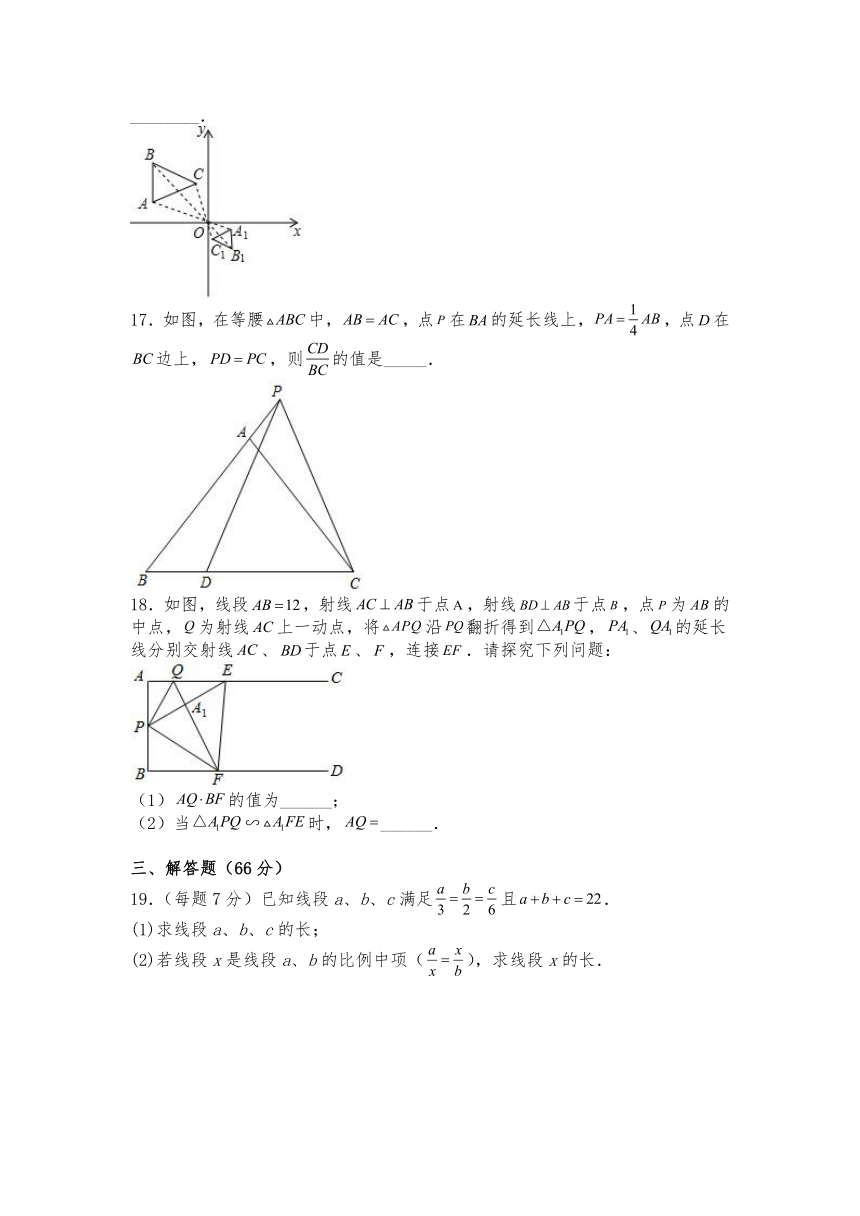
17.如图,在等腰中,,点在的延长线上,,点在边上,,则的值是_____.
18.如图,线段,射线于点,射线于点,点为的中点,为射线上一动点,将沿翻折得到,、的延长线分别交射线、于点、,连接.请探究下列问题:
(1)的值为______;
(2)当∽时,______.
三、解答题(66分)
19.(每题7分)已知线段a、b、c满足且.
(1)求线段a、b、c的长;
(2)若线段x是线段a、b的比例中项(),求线段x的长.
20.(每题7分)如图,l1∥l2∥l3,AD=2,DE=4.
(1)AB=3,求BC;
(2)EF=7.5,BE的长.
21.(每题7分)如图,在中,点D在BC边上,点E在AC边上,且,.求证:
22.(每题7分)李师傅用镜子测量一棵古树的高,但树旁有一条小河,不便测量镜子与树之间的距离,于是他两次利用镜子,第一次把镜子放在点(如图所示),人在点正好在镜中看到树尖;第二次他把镜子放在处,人在处正好看到树尖.已知李师傅眼睛距地面的高度为,量得为,为,为,求树高.
23.(每题7分)在平面直角坐标系中,△ABC的顶点坐标分别为A(0,2)、B(1,3)、C(2,1).
(1)以点O为位似中心,在给定的网格中画出△A'B'C',使△A'B'C'与△ABC位似,且相似比为2;
(2)求出△A'B'C'的面积.
24.(每题7分)如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,连接AP、PD,∠APD=60°.
(1)求证:△ABP∽△PCD;
(2)若PC=2,求CD的长.
25.(每题7分)如图,在矩形中,E是边的中点,于点F.
(1)求证:.
(2)已知,求的长.
26.(每题8分)如图,在正方形中,,为边上的两个三等分点,点关于的对称点为,的延长线交于点.
(1)求证:;
(2)求证:.
27.(每题9分)如图1,在中,于点D,在DA上取点E,使,连接BE、CE.
(1)直接写出CE与AB的位置关系;
(2)如图2,将绕点D旋转,得到(点,分别与点B,E对应),连接,在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致 请说明理由;
(3)如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若,求的长.
答案
一、单选题
A.A.B.C.B.B.C.D.D.C.
二、填空题
11..
12..
13.2,3.
14.①③④
15.8.
16..
17..
18. 36
三、解答题
19.
(1)解:设,则,,,,,解得,则,,.
(2)解:线段是线段、的比例中项,且,,,解得或(舍去),经检验,是所列分式方程的解,即线段的长为.
20.(1)
解:∵l1∥l2∥l3,
∴,
∵AD=2,DE=4,AB=3,
∴,
解得BC=6,
∴BC的长为6;
(2)解:∵l1∥l2∥l3,
∴,
∵AD=2,DE=4,EF=7.5,
∴,
解得BE=5,
∴BE的长为5.
21.∵AB=AD
∴∠B=∠ADB
∵∠DEC=∠B
∴∠ADB=∠DEC
∴∠AED=∠ADC
又∵∠DAE=∠CAD
∴
22.解:根据反射定律可以推出∠ACB=∠ECF,∠AC′B=∠E′C′F′,
∴△BAC∽△FEC、△AC′B∽△E′C′F′,
设AB=x,BC=y
∴
解得.
∴这棵古树的高为10m.
23.(1)
解:如图,△A'B'C'为所作;
(2)△A'B'C'的面积=4×4﹣×2×4﹣×2×2﹣×2×4=6.
24.
(1)证明:∵等边三角形ABC,∴∠B=∠C=60°,∵∠APD=60°,∴∠APB+∠CPD=120°,在△APB中,∠APB+∠BAP=120°,∴∠BAP=∠CPD,∴△ABP∽△PCD;
(2)解:等边三角形边长为3,PC=2,由(1)得△ABP∽△PCD,,∴,∴CD=.答:CD的长为.
25.(1)
证明:∵四边形为矩形,,
∴,
∴,
∴,
∴.
(2)
∵E为的中点,
∴,
∴.
∵,
∴,
∴.
26.(1)
证明:设与的交点为,
,为边上的两个三等分点,
,,
点关于的对称点为,
,
;
(2)
解:,
,
,
,
在和中,
,
,
,,
,
∵,
,
如图,过点作,连接,
,
,,
,
,
,,,
∴,
,
又,
,
,
,
,
点关于的对称点为,
,
,
,,
,
,
,
,
,
又,
△△,
,
,,
,
,
,
,
.
27.(1)
如图,延长CE交AB于H,
∵∠ABC=45°,AD⊥BC,
∴∠ADC=∠ADB=90°,∠ABC=∠DAB=45°,
∵DE=CD,
∴∠DCE=∠DEC=∠AEH=45°,
∴∠BHC=∠BAD+∠AEH=90°,
∴CE⊥AB;
(2)
在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是一致的,理由如下:
如图2,延长交于H,
由旋转可得:CD=,=AD,
∵∠ADC=∠ADB=90°,
∴,
∵,
∴,
,
∵+∠DGC=90°,∠DGC=∠AGH,
∴∠DA+∠AGH=90°,
∴∠AHC=90°,
;
(3)
如图3,过点D作DH于点H,
∵△BED绕点D顺时针旋转30°,
∴,
,
,
∴AD=2DH,AH=DH=,
,
由(2)可知:,
,
∵AD⊥BC,CD=,
∴DG=1,CG=2DG=2,
∴CG=FG=2,
,
∴AG=2GF=4,
∴AD=AG+DG=4+1=5,
∴.
一、单选题(每题3分)
1.已知=5,则的值是( )
A. B.﹣ C. D.
2.已知点C是线段AB的黄金分割点,且,若AB=2,则BC=( )
A. B. C.-1 D.
3.如图,AD∥BE∥CF,AB=3,BC=2,DE=3.6,则EF的值为( )
A.1.8 B.2.4 C.4.8 D.5.4
4.已知一个三角形的三边长分别为2,3,4,与其相似的另一个三角形的周长为36,则它的最长边的长为( )
A.8 B.12 C.16 D.20
5.如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
A.4.5米 B.6米 C.3米 D.4米
6.如图所示,给出下列条件:①;②;③;④,其中单独能够判定的个数为( )
A. B. C. D.
7.如图,和是位似图形,点是位似中心,点,,分别是,,的中点.若的面积为,周长为,则下列说法正确的是( )
A.的面积为 B.的面积为
C.的周长为 D.的周长为
8.如图,在中,,中线,相交于点.,交于点.,则的长为( )
A.5 B.6 C.10 D.12
9.如图在△ABC中,AD是BC边上的高线,BD=1,DC=3,过点A作AE∥BC,连接BE交AD,AC于点F,点G,若BE平分AC,则=( )
A. B. C. D.
10.如图,将正方形纸片沿折叠,使点的对称点落在边上,点的对称点为点,交于点,连接交于点,连接下列四个结论中:①∽;②;③平分;④,其中正确的结论是( )
A.①② B.①②③ C.①③④ D.②③④
二、填空题(每题3分)
11.在比例尺为的某市旅游地图上,某条道路的长为,则这条道路的实际长度为______.
12.已知线段,点是线段的黄金分割点,且,则____.
13.已知,如图,在中,,且.若,则__________,__________.
14.如图,在与中,,,,交于点D,给出下列结论.①;②;③;④.其中正确的结论是__________(填写正确结论的序号).
15.如图所示,诗的意思是:有正方形的城池一座,四面城墙的正中有门,从南门口(点D)直行8里有一塔(点A),自西门(点E)直行2里至点B,切城角(点C)也可以看见塔,问这座方城每面城墙的长是_________里.
16.如图,在平面直角坐标系中,与是位似图形,坐标原点O为位似中心.A与,B与是对应顶点.已知,则的长为________.
17.如图,在等腰中,,点在的延长线上,,点在边上,,则的值是_____.
18.如图,线段,射线于点,射线于点,点为的中点,为射线上一动点,将沿翻折得到,、的延长线分别交射线、于点、,连接.请探究下列问题:
(1)的值为______;
(2)当∽时,______.
三、解答题(66分)
19.(每题7分)已知线段a、b、c满足且.
(1)求线段a、b、c的长;
(2)若线段x是线段a、b的比例中项(),求线段x的长.
20.(每题7分)如图,l1∥l2∥l3,AD=2,DE=4.
(1)AB=3,求BC;
(2)EF=7.5,BE的长.
21.(每题7分)如图,在中,点D在BC边上,点E在AC边上,且,.求证:
22.(每题7分)李师傅用镜子测量一棵古树的高,但树旁有一条小河,不便测量镜子与树之间的距离,于是他两次利用镜子,第一次把镜子放在点(如图所示),人在点正好在镜中看到树尖;第二次他把镜子放在处,人在处正好看到树尖.已知李师傅眼睛距地面的高度为,量得为,为,为,求树高.
23.(每题7分)在平面直角坐标系中,△ABC的顶点坐标分别为A(0,2)、B(1,3)、C(2,1).
(1)以点O为位似中心,在给定的网格中画出△A'B'C',使△A'B'C'与△ABC位似,且相似比为2;
(2)求出△A'B'C'的面积.
24.(每题7分)如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,连接AP、PD,∠APD=60°.
(1)求证:△ABP∽△PCD;
(2)若PC=2,求CD的长.
25.(每题7分)如图,在矩形中,E是边的中点,于点F.
(1)求证:.
(2)已知,求的长.
26.(每题8分)如图,在正方形中,,为边上的两个三等分点,点关于的对称点为,的延长线交于点.
(1)求证:;
(2)求证:.
27.(每题9分)如图1,在中,于点D,在DA上取点E,使,连接BE、CE.
(1)直接写出CE与AB的位置关系;
(2)如图2,将绕点D旋转,得到(点,分别与点B,E对应),连接,在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致 请说明理由;
(3)如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若,求的长.
答案
一、单选题
A.A.B.C.B.B.C.D.D.C.
二、填空题
11..
12..
13.2,3.
14.①③④
15.8.
16..
17..
18. 36
三、解答题
19.
(1)解:设,则,,,,,解得,则,,.
(2)解:线段是线段、的比例中项,且,,,解得或(舍去),经检验,是所列分式方程的解,即线段的长为.
20.(1)
解:∵l1∥l2∥l3,
∴,
∵AD=2,DE=4,AB=3,
∴,
解得BC=6,
∴BC的长为6;
(2)解:∵l1∥l2∥l3,
∴,
∵AD=2,DE=4,EF=7.5,
∴,
解得BE=5,
∴BE的长为5.
21.∵AB=AD
∴∠B=∠ADB
∵∠DEC=∠B
∴∠ADB=∠DEC
∴∠AED=∠ADC
又∵∠DAE=∠CAD
∴
22.解:根据反射定律可以推出∠ACB=∠ECF,∠AC′B=∠E′C′F′,
∴△BAC∽△FEC、△AC′B∽△E′C′F′,
设AB=x,BC=y
∴
解得.
∴这棵古树的高为10m.
23.(1)
解:如图,△A'B'C'为所作;
(2)△A'B'C'的面积=4×4﹣×2×4﹣×2×2﹣×2×4=6.
24.
(1)证明:∵等边三角形ABC,∴∠B=∠C=60°,∵∠APD=60°,∴∠APB+∠CPD=120°,在△APB中,∠APB+∠BAP=120°,∴∠BAP=∠CPD,∴△ABP∽△PCD;
(2)解:等边三角形边长为3,PC=2,由(1)得△ABP∽△PCD,,∴,∴CD=.答:CD的长为.
25.(1)
证明:∵四边形为矩形,,
∴,
∴,
∴,
∴.
(2)
∵E为的中点,
∴,
∴.
∵,
∴,
∴.
26.(1)
证明:设与的交点为,
,为边上的两个三等分点,
,,
点关于的对称点为,
,
;
(2)
解:,
,
,
,
在和中,
,
,
,,
,
∵,
,
如图,过点作,连接,
,
,,
,
,
,,,
∴,
,
又,
,
,
,
,
点关于的对称点为,
,
,
,,
,
,
,
,
,
又,
△△,
,
,,
,
,
,
,
.
27.(1)
如图,延长CE交AB于H,
∵∠ABC=45°,AD⊥BC,
∴∠ADC=∠ADB=90°,∠ABC=∠DAB=45°,
∵DE=CD,
∴∠DCE=∠DEC=∠AEH=45°,
∴∠BHC=∠BAD+∠AEH=90°,
∴CE⊥AB;
(2)
在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是一致的,理由如下:
如图2,延长交于H,
由旋转可得:CD=,=AD,
∵∠ADC=∠ADB=90°,
∴,
∵,
∴,
,
∵+∠DGC=90°,∠DGC=∠AGH,
∴∠DA+∠AGH=90°,
∴∠AHC=90°,
;
(3)
如图3,过点D作DH于点H,
∵△BED绕点D顺时针旋转30°,
∴,
,
,
∴AD=2DH,AH=DH=,
,
由(2)可知:,
,
∵AD⊥BC,CD=,
∴DG=1,CG=2DG=2,
∴CG=FG=2,
,
∴AG=2GF=4,
∴AD=AG+DG=4+1=5,
∴.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
