北师大版七年级下册第四章:三角形全等的判定同步练习(含答案)
文档属性
| 名称 | 北师大版七年级下册第四章:三角形全等的判定同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 61.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-27 00:00:00 | ||
图片预览

文档简介
《三角形全等的判定》同步测试
1. 在△ABC和△DEF中,∠C=∠D,∠B=∠E,要使两三角形全等,需增加条件( ).
A.AB=ED B.AB=FD C.AC=FD D. ∠A=∠F
2. 下列条件能判断△ABC≌△DEF的是( ).
A. ∠A=∠D, ∠C=∠F, ∠B=∠E B. ∠A=∠D,AB+AC=DE+DF
B. ∠A=∠D, ∠B=∠E,AC=DF D. ∠A=∠D,AC=DF,BC=EF
3. △ABC中,∠C=90°,AD为角平分线,BC=32,BD∶DC=9∶7,则点D到AB的距离为( ).
A.18cm B.16cm C.14cm D.12cm
4. ∠MON的边OM上有两点A、C,ON上有两点B、D,且OA=OB,OC=OD,AD,BC交于E,则①△OAD≌△OBC,②△ACE≌△BDE,③连OE,则OE平分∠AOB,以上结论( ).
A.只有一个正确 B.只有一个不正确
C.都正确 D.都不正确
5. △ABC中,∠C=90°,AC=BC,AD为角平分线,DE⊥AB于E,且AB=6cm,则△DEB的周长为( ).
A.4cm B.6cm C.8cm D.10cm
6. 线段OD=DC,A在OC上,B在OD上,且OA=OB,OC=OD,∠COD=60°,∠C=,AC,BC交于E,则∠BED的度数是( ).
A. 60° B.70° C.80° D.50°
1. △ABC和△A′B′C′中,已知∠A=∠B′,AB=B′C′,增加条件 可使
△ABC≌△B′C′A′(ASA).
2. △ABC中∠C=90°,BC>AC,E在BC上,且BE=EA. ∠CAE∶∠B=4∶7,则
∠CEA=_____.
3. △ABC中,∠C=90°,BE为角平分线,ED⊥AB于D,若AE+ED=5cm,则AC=_______.
4. 四边形ABCD中,边AB=DC,AD=BC,∠B=40°,则∠C= .
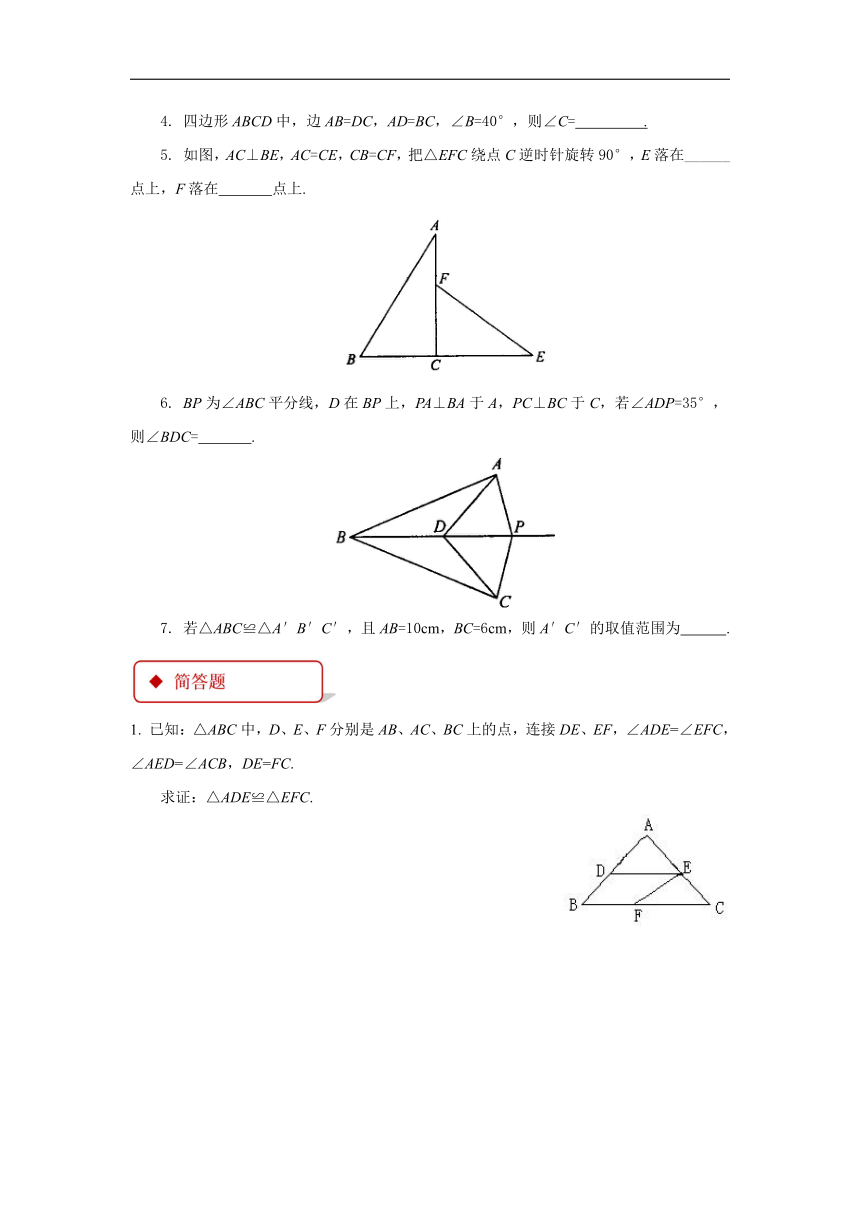
5. 如图,AC⊥BE,AC=CE,CB=CF,把△EFC绕点C逆时针旋转90°,E落在______点上,F落在 点上.
6. BP为∠ABC平分线,D在BP上,PA⊥BA于A,PC⊥BC于C,若∠ADP=35°,则∠BDC= .
7. 若△ABC≌△A′B′C′,且AB=10cm,BC=6cm,则A′C′的取值范围为 .
1. 已知:△ABC中,D、E、F分别是AB、AC、BC上的点,连接DE、EF,∠ADE=∠EFC,∠AED=∠ACB,DE=FC.
求证:△ADE≌△EFC.
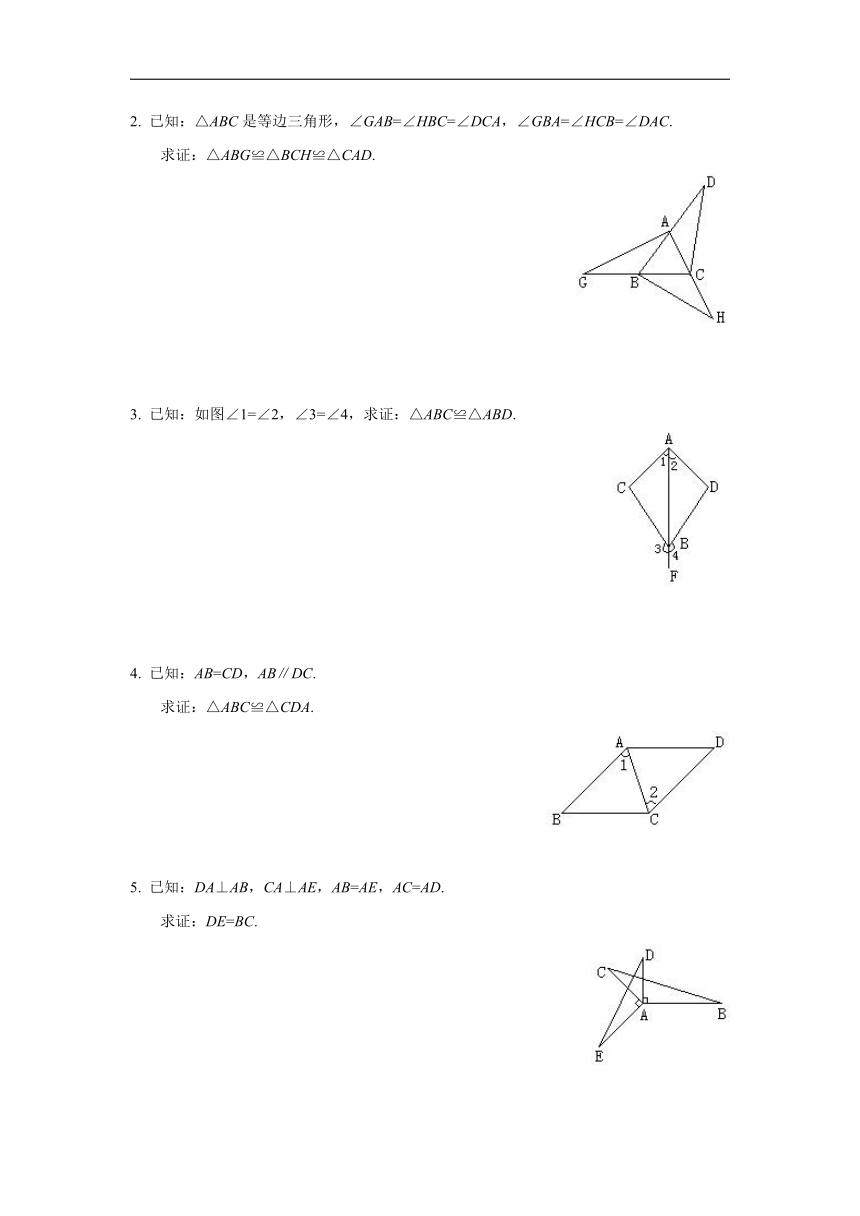
2. 已知:△ABC是等边三角形,∠GAB=∠HBC=∠DCA,∠GBA=∠HCB=∠DAC.
求证:△ABG≌△BCH≌△CAD.
3. 已知:如图∠1=∠2,∠3=∠4,求证:△ABC≌△ABD.
4. 已知:AB=CD,AB∥DC.
求证:△ABC≌△CDA.
5. 已知:DA⊥AB,CA⊥AE,AB=AE,AC=AD.
求证:DE=BC.
6. 已知:△ABC中,AB=AC,D、E分别为AB、AC的中点.
求证:∠ABE=∠ACD
7. 已知:如图AC=BD,∠CAB=∠DBA.
求证:∠CAD=∠DBC.
8. 如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF.求证:AB∥CD.
9. 如图,AE⊥BC,DF⊥BC,E,F是垂足,且AE=DF,AB=DC,求证:∠ABC=∠DCB.
答案与解析
1. C
2. C
3. C
4. C
5. B
6. B
1. ∠B=∠C′
2. 70°
3. 5cm
4. 140°
5. A、B
6. 145°
7. 4<A′C′<16
1. 在△ADE与△EFC中
∴△ADE≌△EFC(ASA)
2. ∵△ABC是等边三角形
∴AB=BC=CA
在△ABG与△BCH中
∴△ABG≌△BCH(ASA)
同理可证:△BCH≌△CAD
∴△ABG≌△BCH≌△CAD
3. ∵∠ABC与∠3互补,∠ABD与∠4互补,又∠3=∠4,
∴∠ABC=∠ABD
在△ABC与△ABD中
∴△ABC≌△ABD(ASA)
4. ∵AB∥CD
∴∠1=∠2
在△ABC与△CDA中
∴△ABC≌△CDA(SAS)
5. ∵DA⊥AB,CA⊥AE
∴∠DAB=∠EAC
∴∠CAB=∠DAE
∴在△CAB与△EAD中
∴△CAB≌△EAD(SAS)
∴DE=BC.
6. ∵AB=AC
D、E分别为AB、AC中点
∴AD=AE
∴在△ADC与△AEB中
∴△ADC≌△AEB(SAS)
∴∠ABE=∠ACD.
7. 证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SAS)
∴∠CBA=∠DAB(全等三角形对应角相等)
又∵∠CAB=∠DBA(已知)
∴∠CAB-∠DAB=∠DBA-∠CBA(等量减等量差相等)
∴∠CAD=∠DBC.
8. ∵CE=BF,∴CE+EF=BF+EF,即BE=CF,
在Rt△AEB和Rt△DCF中,
∴△ABE≌△DCF,
∴∠B=∠C,
∴AB∥CD.
9. ∵AE⊥BC,DF⊥BC,
∴在Rt△ABE和Rt△DCF中,
∴Rt△ABE≌Rt△DCF,
∴∠ABC=∠DCB.
1. 在△ABC和△DEF中,∠C=∠D,∠B=∠E,要使两三角形全等,需增加条件( ).
A.AB=ED B.AB=FD C.AC=FD D. ∠A=∠F
2. 下列条件能判断△ABC≌△DEF的是( ).
A. ∠A=∠D, ∠C=∠F, ∠B=∠E B. ∠A=∠D,AB+AC=DE+DF
B. ∠A=∠D, ∠B=∠E,AC=DF D. ∠A=∠D,AC=DF,BC=EF
3. △ABC中,∠C=90°,AD为角平分线,BC=32,BD∶DC=9∶7,则点D到AB的距离为( ).
A.18cm B.16cm C.14cm D.12cm
4. ∠MON的边OM上有两点A、C,ON上有两点B、D,且OA=OB,OC=OD,AD,BC交于E,则①△OAD≌△OBC,②△ACE≌△BDE,③连OE,则OE平分∠AOB,以上结论( ).
A.只有一个正确 B.只有一个不正确
C.都正确 D.都不正确
5. △ABC中,∠C=90°,AC=BC,AD为角平分线,DE⊥AB于E,且AB=6cm,则△DEB的周长为( ).
A.4cm B.6cm C.8cm D.10cm
6. 线段OD=DC,A在OC上,B在OD上,且OA=OB,OC=OD,∠COD=60°,∠C=,AC,BC交于E,则∠BED的度数是( ).
A. 60° B.70° C.80° D.50°
1. △ABC和△A′B′C′中,已知∠A=∠B′,AB=B′C′,增加条件 可使
△ABC≌△B′C′A′(ASA).
2. △ABC中∠C=90°,BC>AC,E在BC上,且BE=EA. ∠CAE∶∠B=4∶7,则
∠CEA=_____.
3. △ABC中,∠C=90°,BE为角平分线,ED⊥AB于D,若AE+ED=5cm,则AC=_______.
4. 四边形ABCD中,边AB=DC,AD=BC,∠B=40°,则∠C= .
5. 如图,AC⊥BE,AC=CE,CB=CF,把△EFC绕点C逆时针旋转90°,E落在______点上,F落在 点上.
6. BP为∠ABC平分线,D在BP上,PA⊥BA于A,PC⊥BC于C,若∠ADP=35°,则∠BDC= .
7. 若△ABC≌△A′B′C′,且AB=10cm,BC=6cm,则A′C′的取值范围为 .
1. 已知:△ABC中,D、E、F分别是AB、AC、BC上的点,连接DE、EF,∠ADE=∠EFC,∠AED=∠ACB,DE=FC.
求证:△ADE≌△EFC.
2. 已知:△ABC是等边三角形,∠GAB=∠HBC=∠DCA,∠GBA=∠HCB=∠DAC.
求证:△ABG≌△BCH≌△CAD.
3. 已知:如图∠1=∠2,∠3=∠4,求证:△ABC≌△ABD.
4. 已知:AB=CD,AB∥DC.
求证:△ABC≌△CDA.
5. 已知:DA⊥AB,CA⊥AE,AB=AE,AC=AD.
求证:DE=BC.
6. 已知:△ABC中,AB=AC,D、E分别为AB、AC的中点.
求证:∠ABE=∠ACD
7. 已知:如图AC=BD,∠CAB=∠DBA.
求证:∠CAD=∠DBC.
8. 如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF.求证:AB∥CD.
9. 如图,AE⊥BC,DF⊥BC,E,F是垂足,且AE=DF,AB=DC,求证:∠ABC=∠DCB.
答案与解析
1. C
2. C
3. C
4. C
5. B
6. B
1. ∠B=∠C′
2. 70°
3. 5cm
4. 140°
5. A、B
6. 145°
7. 4<A′C′<16
1. 在△ADE与△EFC中
∴△ADE≌△EFC(ASA)
2. ∵△ABC是等边三角形
∴AB=BC=CA
在△ABG与△BCH中
∴△ABG≌△BCH(ASA)
同理可证:△BCH≌△CAD
∴△ABG≌△BCH≌△CAD
3. ∵∠ABC与∠3互补,∠ABD与∠4互补,又∠3=∠4,
∴∠ABC=∠ABD
在△ABC与△ABD中
∴△ABC≌△ABD(ASA)
4. ∵AB∥CD
∴∠1=∠2
在△ABC与△CDA中
∴△ABC≌△CDA(SAS)
5. ∵DA⊥AB,CA⊥AE
∴∠DAB=∠EAC
∴∠CAB=∠DAE
∴在△CAB与△EAD中
∴△CAB≌△EAD(SAS)
∴DE=BC.
6. ∵AB=AC
D、E分别为AB、AC中点
∴AD=AE
∴在△ADC与△AEB中
∴△ADC≌△AEB(SAS)
∴∠ABE=∠ACD.
7. 证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SAS)
∴∠CBA=∠DAB(全等三角形对应角相等)
又∵∠CAB=∠DBA(已知)
∴∠CAB-∠DAB=∠DBA-∠CBA(等量减等量差相等)
∴∠CAD=∠DBC.
8. ∵CE=BF,∴CE+EF=BF+EF,即BE=CF,
在Rt△AEB和Rt△DCF中,
∴△ABE≌△DCF,
∴∠B=∠C,
∴AB∥CD.
9. ∵AE⊥BC,DF⊥BC,
∴在Rt△ABE和Rt△DCF中,
∴Rt△ABE≌Rt△DCF,
∴∠ABC=∠DCB.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
