人教版数学七年级上册 4.3 第2课时角的比较与运算 课件(共29张PPT)
文档属性
| 名称 | 人教版数学七年级上册 4.3 第2课时角的比较与运算 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 434.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-27 15:55:43 | ||
图片预览



文档简介
(共29张PPT)
4.3 角
第2课时 角的比较与运算
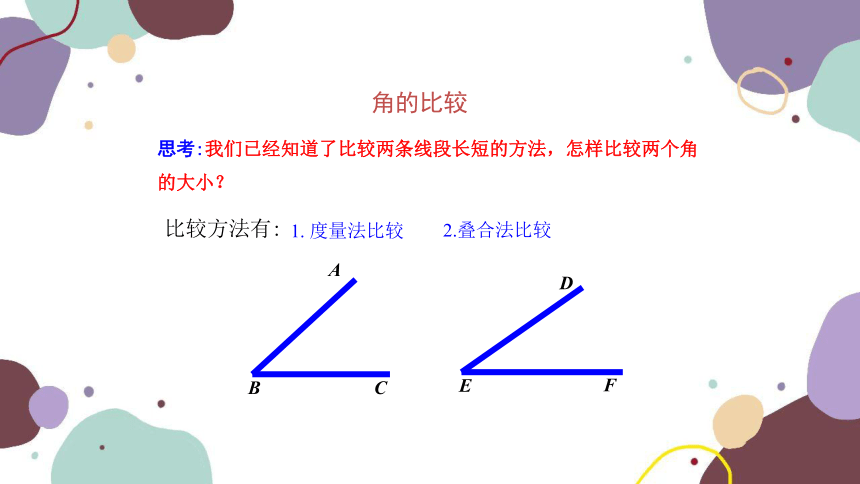
思考:我们已经知道了比较两条线段长短的方法,怎样比较两个角的大小?
B
A
C
E
D
F
比较方法有:
1. 度量法比较
2.叠合法比较
角的比较
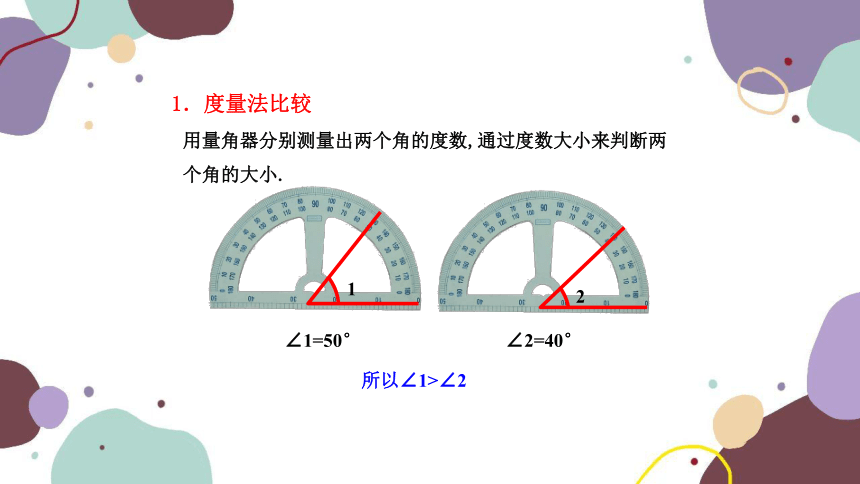
1.度量法比较
∠1=50°
∠2=40°
所以∠1>∠2
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
1
2
2.叠合法比较
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过这两边的位置来判断两个角的大小.
∠1<∠2
∠1>∠2
∠1=∠2
1
2
1
2
2
1
注意:
1.两角的顶点必须重合;
2.一边必须重合,另一边落在重合的一边的同侧.
(“两重一同” )
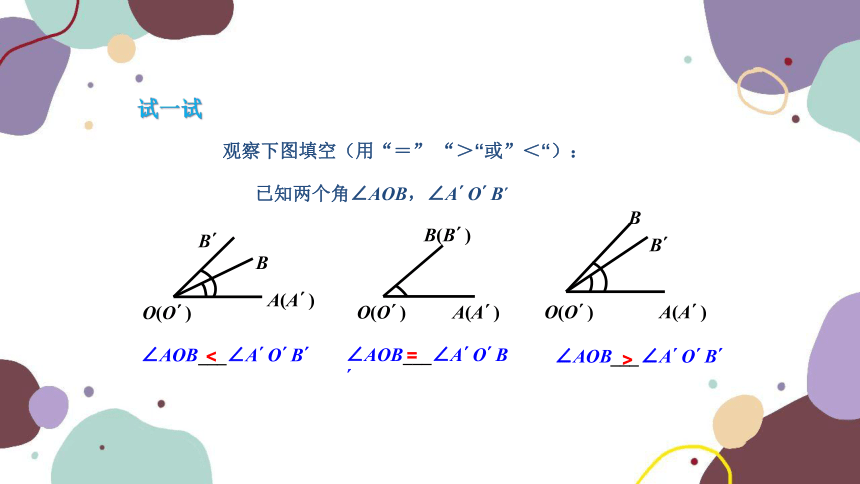
观察下图填空(用“=” “>“或”<“):
已知两个角∠AOB,∠A O B
B(B )
O(O )
A(A )
∠AOB___∠A O B
<
B
B
A(A )
O(O )
∠AOB___∠A O B
A(A )
O(O )
B
B
∠AOB___∠A O B
=
>
试一试
(1)若∠1= ∠2, ∠2= ∠3,则∠1__ ∠3
(2)若∠1 > ∠2, ∠2 > ∠3,则∠1___ ∠3
思 考
归纳:角的大小具有传递性
=
>
角的和与差
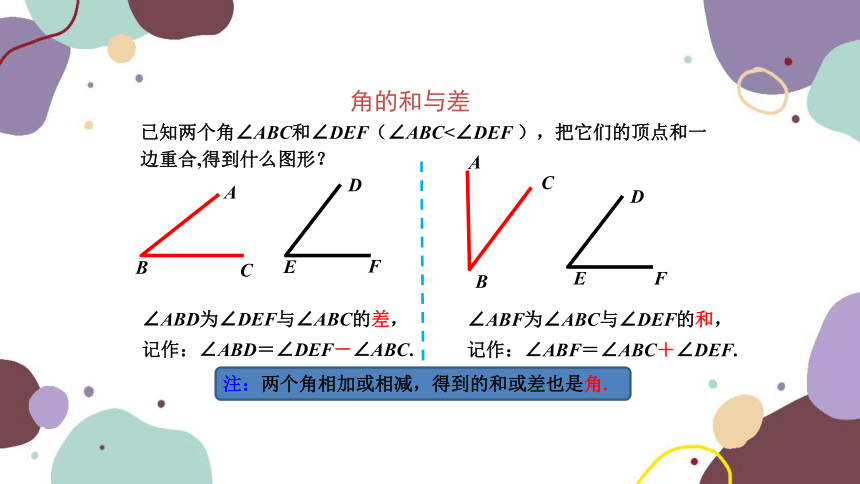
已知两个角∠ABC和∠DEF(∠ABC<∠DEF ),把它们的顶点和一边重合,得到什么图形?
A
B
C
D
E
F
∠ABD为∠DEF与∠ABC的差,
记作:∠ABD=∠DEF-∠ABC.
∠ABF为∠ABC与∠DEF的和,
记作:∠ABF=∠ABC+∠DEF.
A
B
C
D
E
F
注:两个角相加或相减,得到的和或差也是角.
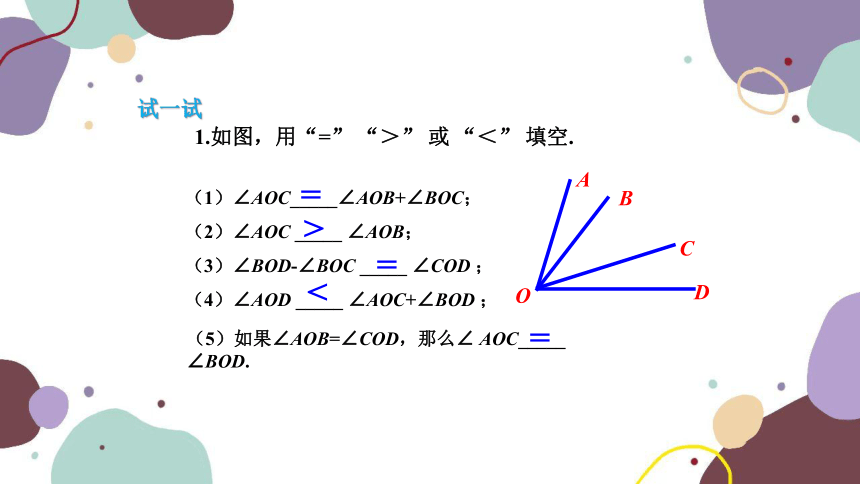
(1)∠AOC_____∠AOB+∠BOC;
(2)∠AOC _____ ∠AOB;
(3)∠BOD-∠BOC _____ ∠COD ;
(4)∠AOD _____ ∠AOC+∠BOD ;
1.如图,用“=” “>” 或 “<” 填空.
D
O
C
B
A
=
>
=
<
=
试一试
(5)如果∠AOB=∠COD,那么∠ AOC_____ ∠BOD.
D
O
C
B
A
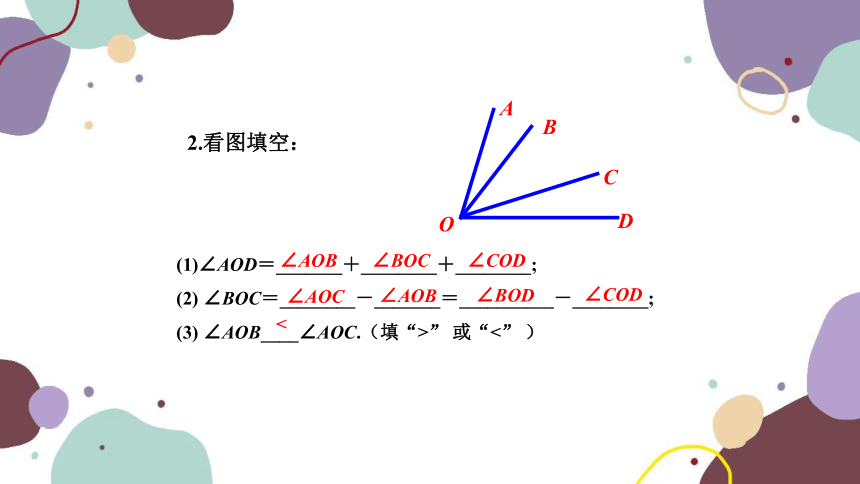
(1)∠AOD=_______+________+________;
(2) ∠BOC=________-_______=__________-________;
(3) ∠AOB____∠AOC.(填“>” 或“<” )
∠AOB
∠BOC
∠COD
∠AOC
∠AOB
∠BOD
∠COD
<
2.看图填空:
15°
75°
实践活动
借助一副三角尺,大家都能画出哪些度数的角?
利用三角尺还可以画出哪些大于0°小于180°的角?
(15°的整数倍)
探究:
75°
15°
15°, 30°,45°,60°, 75°, 90°,105°,120°,135°,150°,165°
M
O
C
A
在一张纸上画出一个∠AOC 并剪下,将这个角对折,使其两边重合,折痕记作OM,它与角两边所成的两个角的大小有什么关系?
∠AOM 和 ∠MOC 相等.
做一做
从一个角的顶点出发,把这个角分成两个相等的角的射线叫做这个角的角平分线.
C
O
A
B
那么∠AOC=2__________=2_______,
∠AOB=∠BOC=_________.
∠AOB
∠BOC
如果OB是∠AOC的平分线,
OB、OC是∠AOD的三等分线.
D
O
A
C
B
⌒
⌒
⌒
类似地:还有角的三等分线 .如下图
从一个角的顶点出发,把这个角分成相等的三个角的射线,叫做这个角的三等分线.
角三等分线的定义
知识要点
∠______=∠_______
A
B
C
D
E
( 角平分线的定义 )
( 角平分线的定义 )
1.看图填空
AD是∠BAC的平分线
BAD
CAD
∠ABC=2∠ABE
_____平分∠_______
BE
ABC
练一练
A
B
C
D
O
∠AOC
∠BOD
AOC
BOD
AOD
解:
C
O
A
B
度、分、秒相减时,要借1作60
如图,O是直线AB上一点,∠AOC=53°17′,求∠BOC的度数.
例1
例题讲解
由题意可得,
∠AOB=180°,∠AOB=∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=126°43′.
例2
度、分、秒是60进制.要把剩余的度化成分
解:180°÷7=25°+5°÷7
=25°+300′÷7
≈25°43′
答:每一份是25°43′的角.
把一个平角7等分,每一份是多少度的角(精确到分)?
解:依题意可知:∠MON是平角.
因为∠MON=∠MOP+∠NOP,
所以∠MOP=∠MON-∠NOP
=180°-58°36′42″
=121°23′18″.
答:∠MOP的度数为121°23′18″.
1.如图,O是直线MN上一点,∠NOP=58°36′42″,求∠MOP的度数.
M
N
P
O
度、分、秒相减时,要借1作60
小试身手
2.把一个周角11等分,每一份是多少度的角(精确到秒)?
解:360°÷11=32°+8°÷11
=32°+480′÷11
=32°43′+7′÷11
=32°43′+420″÷11
≈32°43′ 38″.
答:每一份是32°43′38″的角.
1.角的比较方法
(1)度量法;
(2)叠合法.
2.角的和与差
3.角平分线的定义
课堂小结
C
O
A
B
D
(1)∠AOC=_______ +_________;
(2) ∠BOD= ___________+__________;
(3) ∠AOD= ________+ ____+________;
(4) ∠AOB=∠AOC - _______= ∠AOD- ______.
∠AOB
∠BOC
∠COB
∠COD
∠AOB
∠BOC
∠COD
∠COB
∠BOD
随堂练习
1.看图填空.
(1) ∠B______∠A
(2) ∠DCB _____∠B
(3) ∠DCB______∠A+∠B
2.如图所示: ∠A=70°, ∠B=70°, ∠DCB=140°,用“=” “>”或“<”填空.
=
>
=
A
B
C
D
(1)如果BD是∠ABC的平分线,那么∠1=______= ______.
(2)如果∠ABC=2 ∠2,那么BD是_______的________.
∠2
∠ABC
∠ABC
平分线
C
B
A
D
1
2
3.如图:
4、如图,OC,OD分别是∠AOB ,∠BOE的平分线,
(1)如果∠AOB=70°,∠BOE=60°,
那么∠1+ ∠2= ______.
(2) 如果∠1+ ∠2 =55°,则∠AOE= _____.
A
O
B
C
E
D
1
2
65°
110°
5.若图中∠AOC=34°34′ ,∠BOC=21°51′ ,
则∠AOB=______
A
B
C
O
56°25'
度、分、秒相加时,要满60进1;这里满60'进1°
6.如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
解:因为∠AOD=∠AOB+∠BOD=114°
∠BOD=2∠AOB
所以∠AOB= ∠AOD=38°
因为OC平分∠AOD
所以∠AOC= ∠AOD=57°
所以∠BOC=∠AOC-∠AOB
=57°-38°
=19°.
谢谢
4.3 角
第2课时 角的比较与运算
思考:我们已经知道了比较两条线段长短的方法,怎样比较两个角的大小?
B
A
C
E
D
F
比较方法有:
1. 度量法比较
2.叠合法比较
角的比较
1.度量法比较
∠1=50°
∠2=40°
所以∠1>∠2
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
1
2
2.叠合法比较
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过这两边的位置来判断两个角的大小.
∠1<∠2
∠1>∠2
∠1=∠2
1
2
1
2
2
1
注意:
1.两角的顶点必须重合;
2.一边必须重合,另一边落在重合的一边的同侧.
(“两重一同” )
观察下图填空(用“=” “>“或”<“):
已知两个角∠AOB,∠A O B
B(B )
O(O )
A(A )
∠AOB___∠A O B
<
B
B
A(A )
O(O )
∠AOB___∠A O B
A(A )
O(O )
B
B
∠AOB___∠A O B
=
>
试一试
(1)若∠1= ∠2, ∠2= ∠3,则∠1__ ∠3
(2)若∠1 > ∠2, ∠2 > ∠3,则∠1___ ∠3
思 考
归纳:角的大小具有传递性
=
>
角的和与差
已知两个角∠ABC和∠DEF(∠ABC<∠DEF ),把它们的顶点和一边重合,得到什么图形?
A
B
C
D
E
F
∠ABD为∠DEF与∠ABC的差,
记作:∠ABD=∠DEF-∠ABC.
∠ABF为∠ABC与∠DEF的和,
记作:∠ABF=∠ABC+∠DEF.
A
B
C
D
E
F
注:两个角相加或相减,得到的和或差也是角.
(1)∠AOC_____∠AOB+∠BOC;
(2)∠AOC _____ ∠AOB;
(3)∠BOD-∠BOC _____ ∠COD ;
(4)∠AOD _____ ∠AOC+∠BOD ;
1.如图,用“=” “>” 或 “<” 填空.
D
O
C
B
A
=
>
=
<
=
试一试
(5)如果∠AOB=∠COD,那么∠ AOC_____ ∠BOD.
D
O
C
B
A
(1)∠AOD=_______+________+________;
(2) ∠BOC=________-_______=__________-________;
(3) ∠AOB____∠AOC.(填“>” 或“<” )
∠AOB
∠BOC
∠COD
∠AOC
∠AOB
∠BOD
∠COD
<
2.看图填空:
15°
75°
实践活动
借助一副三角尺,大家都能画出哪些度数的角?
利用三角尺还可以画出哪些大于0°小于180°的角?
(15°的整数倍)
探究:
75°
15°
15°, 30°,45°,60°, 75°, 90°,105°,120°,135°,150°,165°
M
O
C
A
在一张纸上画出一个∠AOC 并剪下,将这个角对折,使其两边重合,折痕记作OM,它与角两边所成的两个角的大小有什么关系?
∠AOM 和 ∠MOC 相等.
做一做
从一个角的顶点出发,把这个角分成两个相等的角的射线叫做这个角的角平分线.
C
O
A
B
那么∠AOC=2__________=2_______,
∠AOB=∠BOC=_________.
∠AOB
∠BOC
如果OB是∠AOC的平分线,
OB、OC是∠AOD的三等分线.
D
O
A
C
B
⌒
⌒
⌒
类似地:还有角的三等分线 .如下图
从一个角的顶点出发,把这个角分成相等的三个角的射线,叫做这个角的三等分线.
角三等分线的定义
知识要点
∠______=∠_______
A
B
C
D
E
( 角平分线的定义 )
( 角平分线的定义 )
1.看图填空
AD是∠BAC的平分线
BAD
CAD
∠ABC=2∠ABE
_____平分∠_______
BE
ABC
练一练
A
B
C
D
O
∠AOC
∠BOD
AOC
BOD
AOD
解:
C
O
A
B
度、分、秒相减时,要借1作60
如图,O是直线AB上一点,∠AOC=53°17′,求∠BOC的度数.
例1
例题讲解
由题意可得,
∠AOB=180°,∠AOB=∠AOC+∠BOC.
∴∠BOC=∠AOB-∠AOC
=180°-53°17′
=126°43′.
例2
度、分、秒是60进制.要把剩余的度化成分
解:180°÷7=25°+5°÷7
=25°+300′÷7
≈25°43′
答:每一份是25°43′的角.
把一个平角7等分,每一份是多少度的角(精确到分)?
解:依题意可知:∠MON是平角.
因为∠MON=∠MOP+∠NOP,
所以∠MOP=∠MON-∠NOP
=180°-58°36′42″
=121°23′18″.
答:∠MOP的度数为121°23′18″.
1.如图,O是直线MN上一点,∠NOP=58°36′42″,求∠MOP的度数.
M
N
P
O
度、分、秒相减时,要借1作60
小试身手
2.把一个周角11等分,每一份是多少度的角(精确到秒)?
解:360°÷11=32°+8°÷11
=32°+480′÷11
=32°43′+7′÷11
=32°43′+420″÷11
≈32°43′ 38″.
答:每一份是32°43′38″的角.
1.角的比较方法
(1)度量法;
(2)叠合法.
2.角的和与差
3.角平分线的定义
课堂小结
C
O
A
B
D
(1)∠AOC=_______ +_________;
(2) ∠BOD= ___________+__________;
(3) ∠AOD= ________+ ____+________;
(4) ∠AOB=∠AOC - _______= ∠AOD- ______.
∠AOB
∠BOC
∠COB
∠COD
∠AOB
∠BOC
∠COD
∠COB
∠BOD
随堂练习
1.看图填空.
(1) ∠B______∠A
(2) ∠DCB _____∠B
(3) ∠DCB______∠A+∠B
2.如图所示: ∠A=70°, ∠B=70°, ∠DCB=140°,用“=” “>”或“<”填空.
=
>
=
A
B
C
D
(1)如果BD是∠ABC的平分线,那么∠1=______= ______.
(2)如果∠ABC=2 ∠2,那么BD是_______的________.
∠2
∠ABC
∠ABC
平分线
C
B
A
D
1
2
3.如图:
4、如图,OC,OD分别是∠AOB ,∠BOE的平分线,
(1)如果∠AOB=70°,∠BOE=60°,
那么∠1+ ∠2= ______.
(2) 如果∠1+ ∠2 =55°,则∠AOE= _____.
A
O
B
C
E
D
1
2
65°
110°
5.若图中∠AOC=34°34′ ,∠BOC=21°51′ ,
则∠AOB=______
A
B
C
O
56°25'
度、分、秒相加时,要满60进1;这里满60'进1°
6.如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,求∠BOC的度数?
A
B
C
D
O
解:因为∠AOD=∠AOB+∠BOD=114°
∠BOD=2∠AOB
所以∠AOB= ∠AOD=38°
因为OC平分∠AOD
所以∠AOC= ∠AOD=57°
所以∠BOC=∠AOC-∠AOB
=57°-38°
=19°.
谢谢
