2.2 振动的描述-高二物理鲁科版选择性必修第一册同步课件(共35张PPT)
文档属性
| 名称 | 2.2 振动的描述-高二物理鲁科版选择性必修第一册同步课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-06-27 00:00:00 | ||
图片预览




文档简介
(共35张PPT)
第二章 机械振动
2.振动的描述
教学目标
CONTENT
01
02
03
知道简谐运动的表达式及式中各物理量的含义
知道简谐运动的振幅、周期、频率的含义
掌握简谐运动的位移图像
说话或唱歌时,用手摸着喉部,能感觉到声带的振动。声音大小发生变化,声带的振动也有变化。一般情况下,女生的音调比男生高。这些现象表明振动具有不同的特征。本节我们将学习描述振动特征的物理量,并用图像和公式描述简谐运动。
新课引入
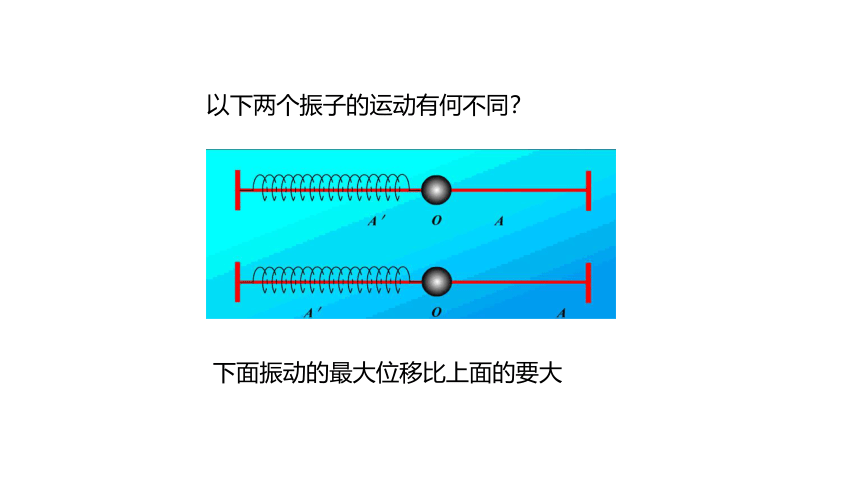
以下两个振子的运动有何不同?
下面振动的最大位移比上面的要大
静止位置
振幅
振幅
:即平衡位置
振动物体离开平衡位置的最大距离。
1.定义:
2.单位: 在国际单位制中,单位是米(m)。
振幅的2倍表示振动物体运动范围的大小。
3.物理意义:
振幅是描述振动强弱的物理量。
振动特征的描述
一
知能提升
振幅
O
O
C
B
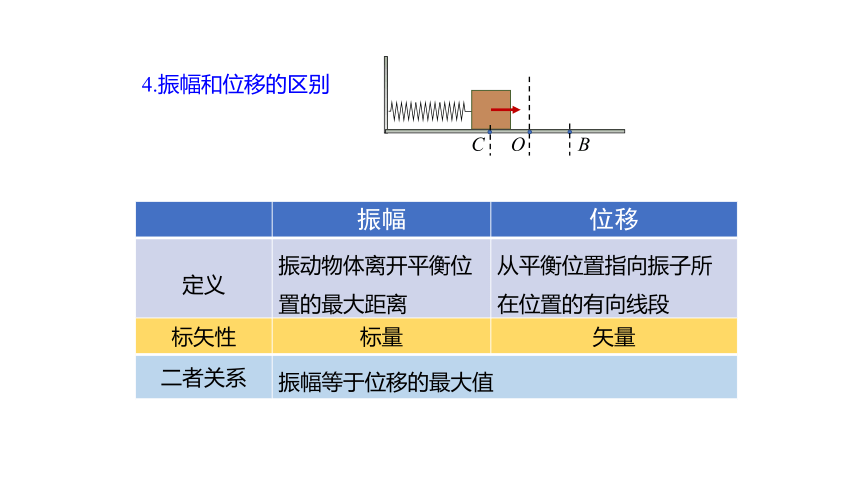
振幅 位移
定义 振动物体离开平衡位置的最大距离 从平衡位置指向振子所在位置的有向线段
二者关系 振幅等于位移的最大值
标矢性 标量 矢量
4.振幅和位移的区别
O
C
B
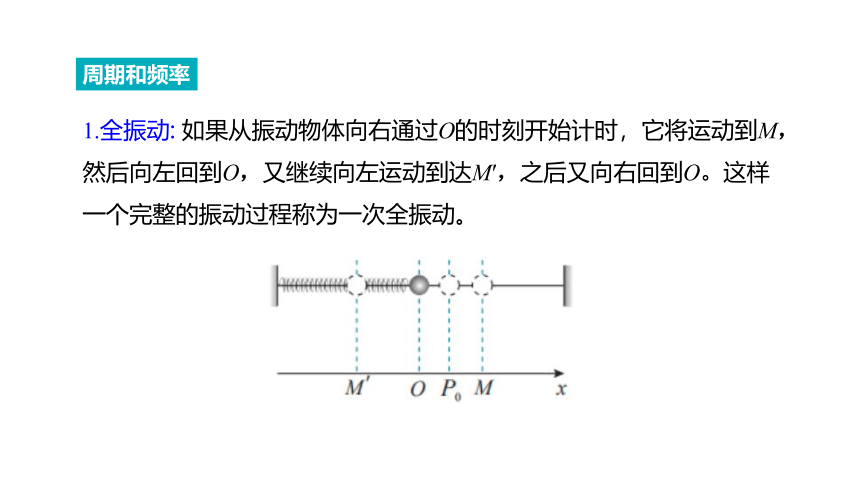
1.全振动: 如果从振动物体向右通过O的时刻开始计时,它将运动到M,然后向左回到O,又继续向左运动到达M′,之后又向右回到O。这样一个完整的振动过程称为一次全振动。
周期和频率
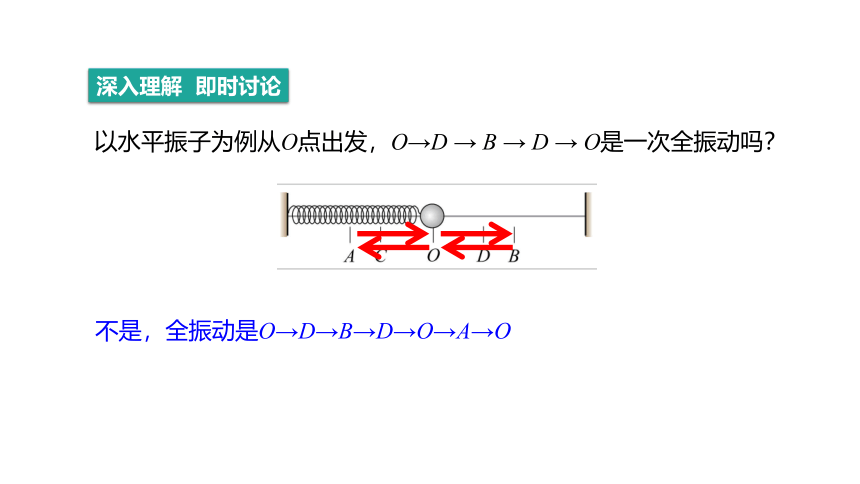
以水平振子为例从O点出发,O→D → B → D → O是一次全振动吗?
不是,全振动是O→D→B→D→O→A→O
深入理解 即时讨论
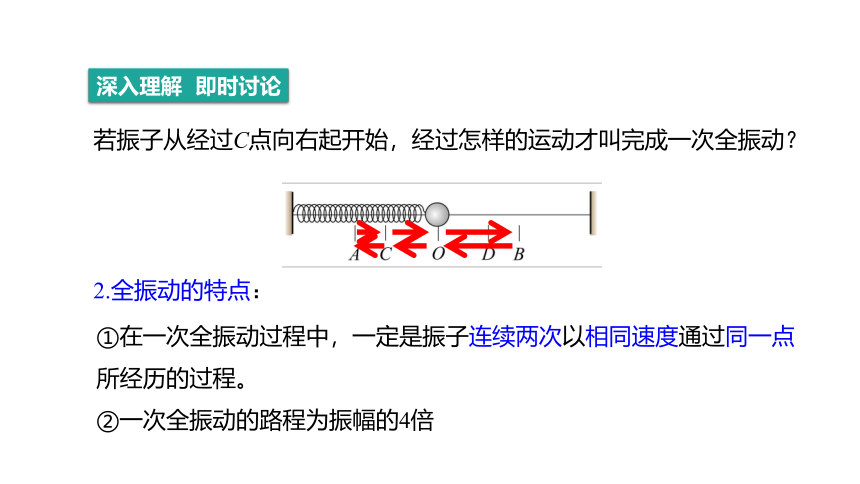
若振子从经过C点向右起开始,经过怎样的运动才叫完成一次全振动?
2.全振动的特点:
①在一次全振动过程中,一定是振子连续两次以相同速度通过同一点所经历的过程。
②一次全振动的路程为振幅的4倍
深入理解 即时讨论
3.周期T:
(1)做简谐运动的物体完成一次全振动所需要的时间,叫作振动的周期.
(2)物理意义:描述振动快慢的物理量.
(3)单位:秒(s)
4.频率f :单位时间内完成的全振动的次数。 单位:赫兹(Hz),f =
5.圆频率ω :ω是一个与周期T成反比、与频率f成正比的量,叫作简谐运动的“圆频率”,是描述振动快慢的物理量.
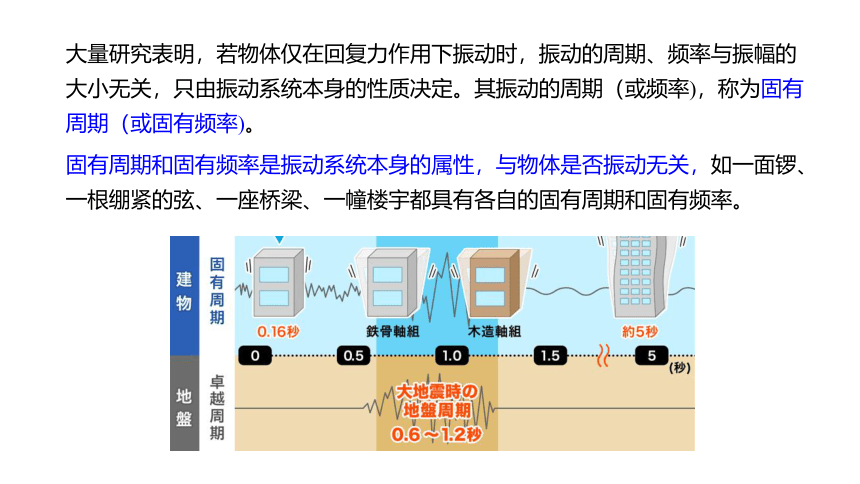
大量研究表明,若物体仅在回复力作用下振动时,振动的周期、频率与振幅的大小无关,只由振动系统本身的性质决定。其振动的周期(或频率),称为固有周期(或固有频率)。
固有周期和固有频率是振动系统本身的属性,与物体是否振动无关,如一面锣、一根绷紧的弦、一座桥梁、一幢楼宇都具有各自的固有周期和固有频率。
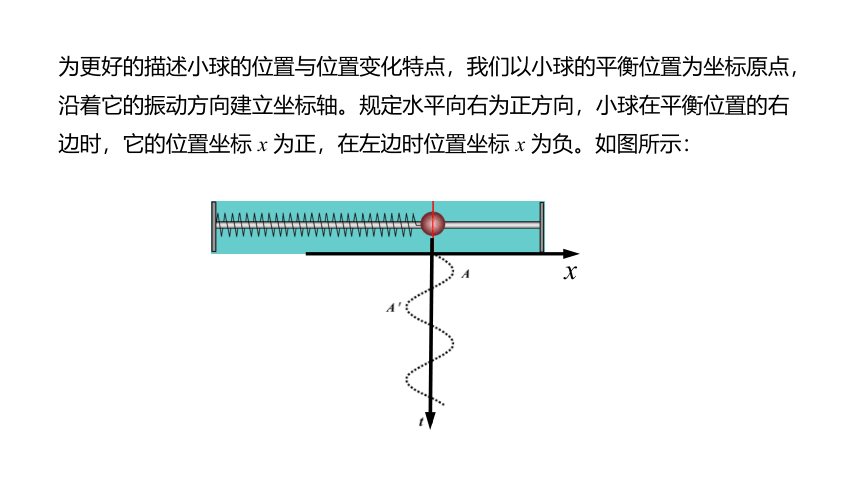
为更好的描述小球的位置与位置变化特点,我们以小球的平衡位置为坐标原点,沿着它的振动方向建立坐标轴。规定水平向右为正方向,小球在平衡位置的右边时,它的位置坐标 x 为正,在左边时位置坐标 x 为负。如图所示:
x
第一个 周期:
时间t(s) 0 t0 2t0 3t0 4t0 5t0 6t0
位移x(cm) -20.0 -17.8 -10.1 0.1 10.3 17.7 20.0
第二个 周期:
时间t(s) 6t0 7t0 8t0 9t0 10t0 11t0 12t0
位移x(cm) 20.0 17.7 10.3 0.1 -10.1 -17.8 -20.0
(1)描点法
图像绘制方法
为什么要匀速拖动白纸?
(2)描图记录法
用纸带上相同位移表示相等的时间。
x
t
v=0.05 m/s
5 cm一格代表1 s
弹簧振子的位移-时间图像。又称为振动图像。
用数码照相机拍摄竖直方向弹簧振子的运动录像,得到分帧照片,依次排列得到图像。
(3)频闪照相
t
x
O
思考:如何理解这就是振子的位移时间图象
描述了振子在各时刻时相对于平衡位置的位移。
频闪照片研究振动图像
二
知能提升
简谐运动的位移图像
简谐运动的振动图像是一条正弦(或余弦)曲线,它能直观地表示做简谐运动物体的位移随时间按正弦(或余弦)规律变化的情况
横坐标:振动时间t
纵坐标:振子相对于平衡位置的位移
描述了质点作简谐运动时,位移随时间变化的规律,它不是质点的轨迹。
t1 t2 t3 t4 t5 t6 t7 t8 t
x
B
P
O
P′
C
从振动图像看周期
①从经过平衡位置到下一次以相同速度经过平衡位置
②从到达最大位移到下一次以相同速度到达最大位移
③从任意位置到下一次以相同速度到达该位置
T
2T
简谐运动物体的位移x与运动时间t之间满足正弦(或余弦)函数关系,位移时间图像是一个正弦 (或余弦) 曲线,那么你能写出它的表达式吗?
t/s
x/m
振幅
圆频率
相位
简谐运动的位移公式
三
知能提升
拓展提升
为了直观地表明简谐运动的三个特征量的物理意义,可用一个圆周运动来表示简谐运动。
t+
O
x
x
t = t
t = 0
·
参考圆
1.相位:当(ωt+φ)确定时,x=Asin (ωt+φ)的函数值也就确定了,即物体做简谐运动的位置状态就确定了。物理学中把(ωt+φ)叫作相位。
φ是t=0时的相位,称为初相位或初相。
2.相位差:指两个简谐运动的相位之差,可以反映出两个简谐运动的步调差异,经常用到的是两个具有相同频率的简谐运动的相位差。
两个具有相同ω的简谐运动,设其初相分别为φ1和φ2,其相位差
Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1.
(1)若Δφ=( φ2 - φ1 )>0, 则2的相位比1的超前;
(2)若Δφ =( φ2 - φ1 )<0, 则2的相位比1的落后。
拓展一步
甲与乙的相位差为0,同相 步调一致
乙与丙的相位差为π, 反相 步调相反
特别提醒:
同相: Δφ=0时,两运动步调完全相同
反相: Δφ=π(或-π)时,两运动步调相反
甲
乙
丙
例.如图,弹簧振子的平衡位置为 O 点,在 B、C两点之间做简谐运动。B、C 相距 20 cm。小球经过 B 点时开始计时,经过 0.5 s 首次到达 C 点。
(1)画出小球在第一个周期内的 x-t 图像。
(2)求 5 s 内小球通过的路程及 5 s 末小球的位移。
【思考】
振子的振幅为多大?振子的周期为多大?
振子的圆频率为多少?振子的初相是多大?
典例精析
解:(1)B、C 相距 20 cm,知小球的振幅为 10 cm;
经过 B 点时开始计时,经过 0.5 s 首次到达 C 点,知周期为1 s ;
由ω=2πf 知,ω=2π;小球的初相位为 ;
综上知小球的振动表达式为
例.如图,弹簧振子的平衡位置为 O 点,在 B、C两点之间做简谐运动。B、C 相距 20 cm。小球经过 B 点时开始计时,经过 0.5 s 首次到达 C 点。
(1)画出小球在第一个周期内的 x-t 图像。
(2)求 5 s 内小球通过的路程及 5 s 末小球的位移。
(2)由于振动的周期 T = 1s,
所以在时间 t = 5s 内,小球一共做了 5 次全振动。
振动物体在一个周期内的路程一定为 4A= 0.4 m,
所以小球运动的路程为 s = 5×0.4 m = 2 m ;
经过 5 次全振动后,小球正好回到 B 点,所以小球的位移为 0.1 m。
例.如图,弹簧振子的平衡位置为 O 点,在 B、C两点之间做简谐运动。B、C 相距 20 cm。小球经过 B 点时开始计时,经过 0.5 s 首次到达 C 点。
(1)画出小球在第一个周期内的 x-t 图像。
(2)求 5 s 内小球通过的路程及 5 s 末小球的位移。
一、振动特征的描述
二、简谐运动的位移图像
三、简谐运动的位移公式
课堂小结
1.一个做简谐运动的质点,它的振幅是4 cm,频率是2.5 Hz,该质点从平衡位置开始经过2.5 s后,位移的大小和经过的路程为( )
A.4 cm 10 cm B.4 cm 100 cm
C.0 24 cm D.0 100 cm
跟踪练习
解析:质点的振动周期T==0.4 s,故时间t=T=T,所以2.5 s末质点在最大位移处,位移大小为4 cm,质点通过的路程为s=4A·=4×4× cm=100 cm,B正确。
B
2.周期为2 s的简谐运动,在30 s内通过的路程是60 cm,则在此时间内振子经过平衡位置的次数和振子的振幅分别为( )
A.15次 2 cm B.30次 1 cm
C.15次 1 cm D.60次 2 cm
解析:振子完成一次全振动经过轨迹上每点的位置两次(除最大位移外),而每次全振动振子通过的路程为4个振幅。
B
3.(多选)物体A做简谐运动的振动方程是xA=3sinm,物体B做简谐运动的振动方程是xB=5sinm。比较A、B的运动( )
A.振幅是矢量,A的振幅是6 m,B的振幅是10 m
B.周期是标量,A、B周期相等,都为100 s
C.A振动的频率fA等于B振动的频率fB
D.A的相位始终超前B的相位
解析:振幅是标量,A、B的振动范围分别是6 m、10 m,但振幅分别为3 m、5 m,选项A错误;A、B的周期均为 s=6.28×10-2 s,选项B错误;因为TA=TB,故fA=fB,选项C正确;Δφ=φA-φB= ,为定值,选项D正确。
CD
4.(多选)一做简谐运动的物体的振动图像如图所示,下列说法正确的是( )
A.振动周期是2×10-2 s
B.第2个10-2 s内物体的位移变化量是-10 cm
C.物体的振动频率为25 Hz
D.物体的振幅是10 cm
解析:周期是完成一次全振动所用的时间,所以周期是4×10-2 s,故选项A错误;又f= ,所以 f=25 Hz,则选项C正确;振动物体离开平衡位置的最大距离表示振幅,所以振幅A=10 cm,则选项D正确;第2个10-2 s内的初位置是10 cm,末位置是0,位移变化量x=x2-x1=-10 cm,选项B正确。
BCD
5.两个简谐运动分别为x1=4asin(4πbt+ )和x2=2asin(4πbt+ ),求它们的振幅之比,各自的频率,以及它们的相位差。
解:
振幅之比=
x=Asin(ωt+φ)
两者频率均为:
两者相位差为:
两振动为反相
6.如图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做往复运动,取A到B为正方向,振子的位移 x 随时间 t 的变化如图乙所示,下列说法正确的是( )
A.t = 0.2 s时,振子在O点右侧6 cm处
B.t = 0.8 s时,振子的速度方向为负方向
C.t = 0.4 s和t = 1.2 s时,振子的加速度完全相同
D.t = 0.4 s到t = 0.8 s的时间内,振子的速度逐渐减小
解析:在0 ~ 0.4 s内,振子做变减速运动,不是匀速运动,所以t = 0.2 s时,振子不在O点右侧6 cm处,故A错误;由题图乙知,t = 0.8 s时,图像的斜率为负,说明振子的速度为负,故B正确;t = 0.4 s和t = 1.2 s时振子的位移方向相反,可知加速度方向相反,故C错误; t = 0.4 s到t = 0.8 s的时间内,振子的位移减小,向平衡位置靠近,速度增大,故D错误。
答案:B
本节内容结束
第二章 机械振动
2.振动的描述
教学目标
CONTENT
01
02
03
知道简谐运动的表达式及式中各物理量的含义
知道简谐运动的振幅、周期、频率的含义
掌握简谐运动的位移图像
说话或唱歌时,用手摸着喉部,能感觉到声带的振动。声音大小发生变化,声带的振动也有变化。一般情况下,女生的音调比男生高。这些现象表明振动具有不同的特征。本节我们将学习描述振动特征的物理量,并用图像和公式描述简谐运动。
新课引入
以下两个振子的运动有何不同?
下面振动的最大位移比上面的要大
静止位置
振幅
振幅
:即平衡位置
振动物体离开平衡位置的最大距离。
1.定义:
2.单位: 在国际单位制中,单位是米(m)。
振幅的2倍表示振动物体运动范围的大小。
3.物理意义:
振幅是描述振动强弱的物理量。
振动特征的描述
一
知能提升
振幅
O
O
C
B
振幅 位移
定义 振动物体离开平衡位置的最大距离 从平衡位置指向振子所在位置的有向线段
二者关系 振幅等于位移的最大值
标矢性 标量 矢量
4.振幅和位移的区别
O
C
B
1.全振动: 如果从振动物体向右通过O的时刻开始计时,它将运动到M,然后向左回到O,又继续向左运动到达M′,之后又向右回到O。这样一个完整的振动过程称为一次全振动。
周期和频率
以水平振子为例从O点出发,O→D → B → D → O是一次全振动吗?
不是,全振动是O→D→B→D→O→A→O
深入理解 即时讨论
若振子从经过C点向右起开始,经过怎样的运动才叫完成一次全振动?
2.全振动的特点:
①在一次全振动过程中,一定是振子连续两次以相同速度通过同一点所经历的过程。
②一次全振动的路程为振幅的4倍
深入理解 即时讨论
3.周期T:
(1)做简谐运动的物体完成一次全振动所需要的时间,叫作振动的周期.
(2)物理意义:描述振动快慢的物理量.
(3)单位:秒(s)
4.频率f :单位时间内完成的全振动的次数。 单位:赫兹(Hz),f =
5.圆频率ω :ω是一个与周期T成反比、与频率f成正比的量,叫作简谐运动的“圆频率”,是描述振动快慢的物理量.
大量研究表明,若物体仅在回复力作用下振动时,振动的周期、频率与振幅的大小无关,只由振动系统本身的性质决定。其振动的周期(或频率),称为固有周期(或固有频率)。
固有周期和固有频率是振动系统本身的属性,与物体是否振动无关,如一面锣、一根绷紧的弦、一座桥梁、一幢楼宇都具有各自的固有周期和固有频率。
为更好的描述小球的位置与位置变化特点,我们以小球的平衡位置为坐标原点,沿着它的振动方向建立坐标轴。规定水平向右为正方向,小球在平衡位置的右边时,它的位置坐标 x 为正,在左边时位置坐标 x 为负。如图所示:
x
第一个 周期:
时间t(s) 0 t0 2t0 3t0 4t0 5t0 6t0
位移x(cm) -20.0 -17.8 -10.1 0.1 10.3 17.7 20.0
第二个 周期:
时间t(s) 6t0 7t0 8t0 9t0 10t0 11t0 12t0
位移x(cm) 20.0 17.7 10.3 0.1 -10.1 -17.8 -20.0
(1)描点法
图像绘制方法
为什么要匀速拖动白纸?
(2)描图记录法
用纸带上相同位移表示相等的时间。
x
t
v=0.05 m/s
5 cm一格代表1 s
弹簧振子的位移-时间图像。又称为振动图像。
用数码照相机拍摄竖直方向弹簧振子的运动录像,得到分帧照片,依次排列得到图像。
(3)频闪照相
t
x
O
思考:如何理解这就是振子的位移时间图象
描述了振子在各时刻时相对于平衡位置的位移。
频闪照片研究振动图像
二
知能提升
简谐运动的位移图像
简谐运动的振动图像是一条正弦(或余弦)曲线,它能直观地表示做简谐运动物体的位移随时间按正弦(或余弦)规律变化的情况
横坐标:振动时间t
纵坐标:振子相对于平衡位置的位移
描述了质点作简谐运动时,位移随时间变化的规律,它不是质点的轨迹。
t1 t2 t3 t4 t5 t6 t7 t8 t
x
B
P
O
P′
C
从振动图像看周期
①从经过平衡位置到下一次以相同速度经过平衡位置
②从到达最大位移到下一次以相同速度到达最大位移
③从任意位置到下一次以相同速度到达该位置
T
2T
简谐运动物体的位移x与运动时间t之间满足正弦(或余弦)函数关系,位移时间图像是一个正弦 (或余弦) 曲线,那么你能写出它的表达式吗?
t/s
x/m
振幅
圆频率
相位
简谐运动的位移公式
三
知能提升
拓展提升
为了直观地表明简谐运动的三个特征量的物理意义,可用一个圆周运动来表示简谐运动。
t+
O
x
x
t = t
t = 0
·
参考圆
1.相位:当(ωt+φ)确定时,x=Asin (ωt+φ)的函数值也就确定了,即物体做简谐运动的位置状态就确定了。物理学中把(ωt+φ)叫作相位。
φ是t=0时的相位,称为初相位或初相。
2.相位差:指两个简谐运动的相位之差,可以反映出两个简谐运动的步调差异,经常用到的是两个具有相同频率的简谐运动的相位差。
两个具有相同ω的简谐运动,设其初相分别为φ1和φ2,其相位差
Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1.
(1)若Δφ=( φ2 - φ1 )>0, 则2的相位比1的超前;
(2)若Δφ =( φ2 - φ1 )<0, 则2的相位比1的落后。
拓展一步
甲与乙的相位差为0,同相 步调一致
乙与丙的相位差为π, 反相 步调相反
特别提醒:
同相: Δφ=0时,两运动步调完全相同
反相: Δφ=π(或-π)时,两运动步调相反
甲
乙
丙
例.如图,弹簧振子的平衡位置为 O 点,在 B、C两点之间做简谐运动。B、C 相距 20 cm。小球经过 B 点时开始计时,经过 0.5 s 首次到达 C 点。
(1)画出小球在第一个周期内的 x-t 图像。
(2)求 5 s 内小球通过的路程及 5 s 末小球的位移。
【思考】
振子的振幅为多大?振子的周期为多大?
振子的圆频率为多少?振子的初相是多大?
典例精析
解:(1)B、C 相距 20 cm,知小球的振幅为 10 cm;
经过 B 点时开始计时,经过 0.5 s 首次到达 C 点,知周期为1 s ;
由ω=2πf 知,ω=2π;小球的初相位为 ;
综上知小球的振动表达式为
例.如图,弹簧振子的平衡位置为 O 点,在 B、C两点之间做简谐运动。B、C 相距 20 cm。小球经过 B 点时开始计时,经过 0.5 s 首次到达 C 点。
(1)画出小球在第一个周期内的 x-t 图像。
(2)求 5 s 内小球通过的路程及 5 s 末小球的位移。
(2)由于振动的周期 T = 1s,
所以在时间 t = 5s 内,小球一共做了 5 次全振动。
振动物体在一个周期内的路程一定为 4A= 0.4 m,
所以小球运动的路程为 s = 5×0.4 m = 2 m ;
经过 5 次全振动后,小球正好回到 B 点,所以小球的位移为 0.1 m。
例.如图,弹簧振子的平衡位置为 O 点,在 B、C两点之间做简谐运动。B、C 相距 20 cm。小球经过 B 点时开始计时,经过 0.5 s 首次到达 C 点。
(1)画出小球在第一个周期内的 x-t 图像。
(2)求 5 s 内小球通过的路程及 5 s 末小球的位移。
一、振动特征的描述
二、简谐运动的位移图像
三、简谐运动的位移公式
课堂小结
1.一个做简谐运动的质点,它的振幅是4 cm,频率是2.5 Hz,该质点从平衡位置开始经过2.5 s后,位移的大小和经过的路程为( )
A.4 cm 10 cm B.4 cm 100 cm
C.0 24 cm D.0 100 cm
跟踪练习
解析:质点的振动周期T==0.4 s,故时间t=T=T,所以2.5 s末质点在最大位移处,位移大小为4 cm,质点通过的路程为s=4A·=4×4× cm=100 cm,B正确。
B
2.周期为2 s的简谐运动,在30 s内通过的路程是60 cm,则在此时间内振子经过平衡位置的次数和振子的振幅分别为( )
A.15次 2 cm B.30次 1 cm
C.15次 1 cm D.60次 2 cm
解析:振子完成一次全振动经过轨迹上每点的位置两次(除最大位移外),而每次全振动振子通过的路程为4个振幅。
B
3.(多选)物体A做简谐运动的振动方程是xA=3sinm,物体B做简谐运动的振动方程是xB=5sinm。比较A、B的运动( )
A.振幅是矢量,A的振幅是6 m,B的振幅是10 m
B.周期是标量,A、B周期相等,都为100 s
C.A振动的频率fA等于B振动的频率fB
D.A的相位始终超前B的相位
解析:振幅是标量,A、B的振动范围分别是6 m、10 m,但振幅分别为3 m、5 m,选项A错误;A、B的周期均为 s=6.28×10-2 s,选项B错误;因为TA=TB,故fA=fB,选项C正确;Δφ=φA-φB= ,为定值,选项D正确。
CD
4.(多选)一做简谐运动的物体的振动图像如图所示,下列说法正确的是( )
A.振动周期是2×10-2 s
B.第2个10-2 s内物体的位移变化量是-10 cm
C.物体的振动频率为25 Hz
D.物体的振幅是10 cm
解析:周期是完成一次全振动所用的时间,所以周期是4×10-2 s,故选项A错误;又f= ,所以 f=25 Hz,则选项C正确;振动物体离开平衡位置的最大距离表示振幅,所以振幅A=10 cm,则选项D正确;第2个10-2 s内的初位置是10 cm,末位置是0,位移变化量x=x2-x1=-10 cm,选项B正确。
BCD
5.两个简谐运动分别为x1=4asin(4πbt+ )和x2=2asin(4πbt+ ),求它们的振幅之比,各自的频率,以及它们的相位差。
解:
振幅之比=
x=Asin(ωt+φ)
两者频率均为:
两者相位差为:
两振动为反相
6.如图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做往复运动,取A到B为正方向,振子的位移 x 随时间 t 的变化如图乙所示,下列说法正确的是( )
A.t = 0.2 s时,振子在O点右侧6 cm处
B.t = 0.8 s时,振子的速度方向为负方向
C.t = 0.4 s和t = 1.2 s时,振子的加速度完全相同
D.t = 0.4 s到t = 0.8 s的时间内,振子的速度逐渐减小
解析:在0 ~ 0.4 s内,振子做变减速运动,不是匀速运动,所以t = 0.2 s时,振子不在O点右侧6 cm处,故A错误;由题图乙知,t = 0.8 s时,图像的斜率为负,说明振子的速度为负,故B正确;t = 0.4 s和t = 1.2 s时振子的位移方向相反,可知加速度方向相反,故C错误; t = 0.4 s到t = 0.8 s的时间内,振子的位移减小,向平衡位置靠近,速度增大,故D错误。
答案:B
本节内容结束
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
