2.3 单摆-高二物理鲁科版选择性必修第一册同步课件(共25张PPT)
文档属性
| 名称 | 2.3 单摆-高二物理鲁科版选择性必修第一册同步课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-06-27 15:18:41 | ||
图片预览





文档简介
(共25张PPT)
第二章 机械振动
3.单摆
教学目标
CONTENT
01
02
03
掌握单摆振动的周期公式
知道什么是单摆
会探究影响单摆周期公式的因素
生活中,我们常看到一些小振幅的摆动现象,类似简谐运动。
新课引入
当摆钟做小振幅的摆动时,可近似看作简谐运动,本节我们将在建立单摆模型的基础上,学习单摆摆动的规律
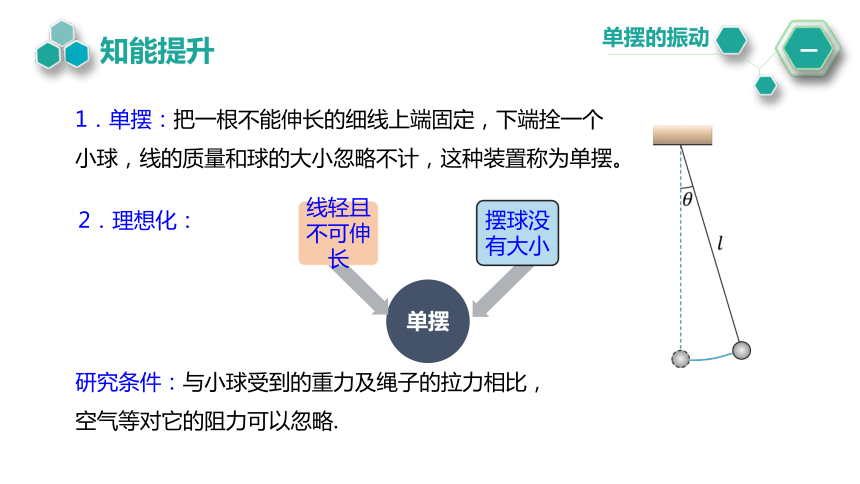
1.单摆:把一根不能伸长的细线上端固定,下端拴一个小球,线的质量和球的大小忽略不计,这种装置称为单摆。
2.理想化:
研究条件:与小球受到的重力及绳子的拉力相比,空气等对它的阻力可以忽略.
单摆的振动
一
知能提升
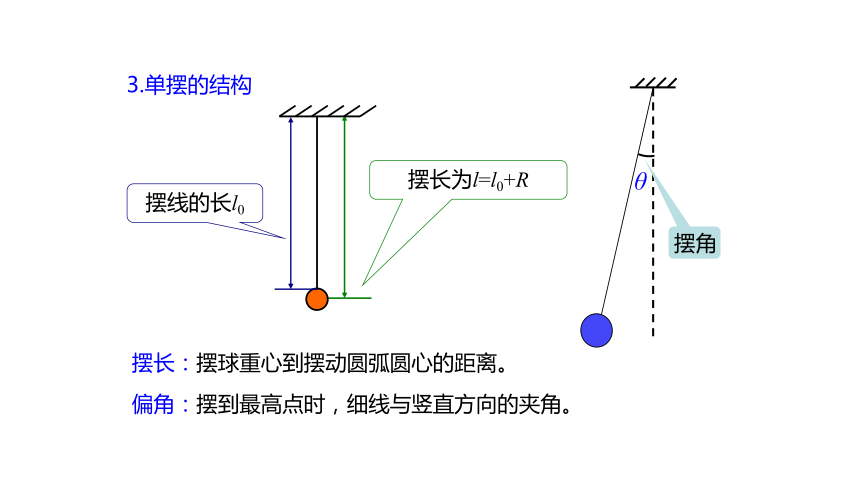
3.单摆的结构
θ
摆角
摆长:摆球重心到摆动圆弧圆心的距离。
偏角:摆到最高点时,细线与竖直方向的夹角。
摆线的长l0
摆长为l=l0+R
用什么方法探究单摆的振动是否为简谐运动?
1.位移与时间的关系是否满足正弦关系(x–t 图像法)
2.回复力与位移是否成正比且方向相反(F=-kx)
思考与讨论
B
A
O
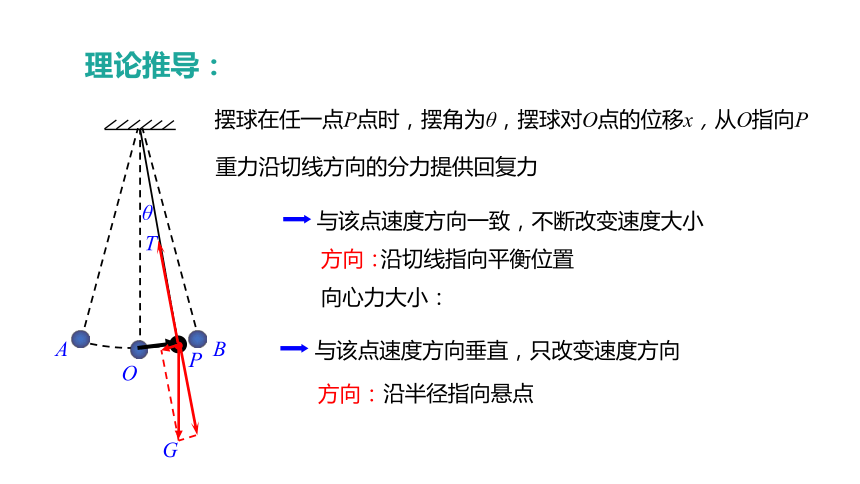
方向:
沿切线指向平衡位置
P
θ
T
G
向心力大小:
与该点速度方向一致,不断改变速度大小
与该点速度方向垂直,只改变速度方向
方向:
沿半径指向悬点
理论推导:
摆球在任一点P点时,摆角为θ,摆球对O点的位移x,从O指向P
重力沿切线方向的分力提供回复力
P
O
θ
T
G
θ
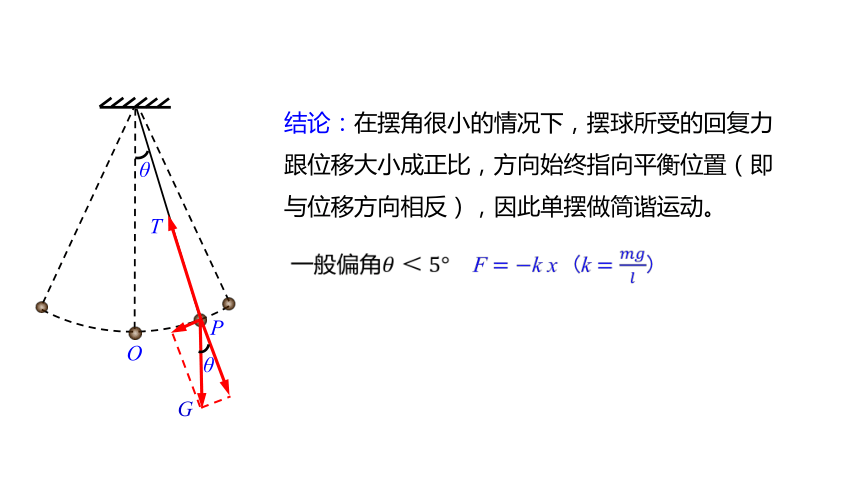
F回=Mgsin θ
角度 弧度值θ sin θ
5° 0.08727 0.08716
4° 0.06981 0.06976
3° 0.05236 0.05234
2° 0.03491 0.03490
1° 0.01754 0.01754
当θ较小时,sinθ θ
位移方向与回复力方向相反F x
可以写成:F k x
结论:在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动。
一般偏角 F k x (k )
P
O
θ
T
G
θ
如图 ,细线下悬挂一个除去了柱塞的注射器,注射器内装上墨汁。当注射器摆动时,沿着垂直于摆动的方向匀速拖动木板,观察留在木板上的墨汁图样。
t
x
O
通过图像,可看出注射器的摆动是简谐运动
做一做
单摆的周期与哪些因素有关呢?
单摆的周期
二
知能提升
猜想:
1.与振幅有关
2.与摆球的质量有关
3.与摆长有关
思考与讨论
探究一:探究周期与振幅的关系
次数 1 2 3 4 5 6
20次全振动时间/s 37.72 37.78 37.82 37.65 37.83 37.84
周期/s 1.886 1.889 1.891 1.883 1.892 1.892
实验表明:单摆周期与振幅无关,这是摆的等时性。
做一做
探究二:探究周期与摆球质量的关系
实验思想:相同摆长,相同尺寸、不同质量的摆球。
实验表明:单摆周期与摆球质量无关
探究三:探究周期与摆长的关系
实验思想:改变摆长,重复多次实验,记录20个周期
数据记录如下表
实验次数 摆长cm 周期T(s) 20次周期(s)
1 30.95 1.12 22.32
5 49.90 1.42 28.34
9 76.95 1.76 35.15
10 82.75 1.82 36.44
13 93.95 1.95 38.98
16 109.45 2.10 41.98
19 135.95 2.34 46.78
1.单摆的周期与振幅无关——单摆的等时性。
2.单摆的周期与摆球的质量无关。
3.单摆的周期与摆长有关——摆长越长,周期越大。
【实验表明】
荷兰物理学家惠更斯(1629-1695)通过实验进一步得出:
单摆做简谐运动的周期跟摆长的算数平方根成正比,跟重力加速度的算数平方根成反比.
该式是个近似公式,由它算出的周期与精确值之间的差别随着偏角的增加而增加。当偏角为5 时两者相差0.01%
例.一个摆长为2 m的单摆,在地球上某地振动时,测得完成100次全振动所用的时间为284 s。
(1)求当地的重力加速度g的大小。
(2)把该单摆拿到月球上去,已知月球上的重力加速度是1.60 m/s2,则该单摆振动周期是多少
典例精析
解析: (1)周期T= s=2.84 s
由周期公式T=2π得,g= m/s2=9.78 m/s2。
(2)T'=2π=2×3.14× s=7.02 s。
一、单摆的振动:在小角度下,单摆是简谐运动
二、单摆的周期:
课堂小结
1.关于单摆摆球在运动过程中的受力,下列结论正确的是( )
A.摆球受重力、摆线的拉力作用
B.摆球受重力、摆线的拉力、回复力作用
C.摆球的回复力为零时,向心力最大
D.摆球的回复力最大时,摆线中的拉力大小比摆球的重力大
解析:单摆在运动过程中,摆球受重力和摆线的拉力,重力沿圆弧切线的分力提供回复力,故A对、B错;在平衡位置处,回复力为零,速度最大,向心力F向= 最大,选项C正确;当回复力最大时,摆球在最大位移处,速度为零,向心力为零,则拉力等于重力沿半径方向的分力,即拉力小于重力,选项D错误。
跟踪练习
AC
2.下列有关单摆运动过程中的受力,说法正确的是( )
A.单摆运动的回复力是重力和摆线拉力的合力
B.单摆运动的回复力是重力沿圆弧切线方向的分力
C.单摆经过平衡位置时合力为零
D.单摆运动的回复力是摆线拉力的一个分力
解析:单摆的回复力是重力沿圆弧切线方向的分力,故选项B正确,A、D错误;单摆经过平衡位置时,回复力为零,向心力最大,其合外力不为零,所以选项C错误。
B
3.(多选)单摆是为研究振动而抽象出的理想化模型,其理想化条件是( )
A.摆线质量不计
B.摆线长度不伸缩
C.摆球的直径比摆线长度短得多
D.只要是单摆的运动就是一种简谐运动
解析:单摆由摆线和摆球组成,摆线只计长度不计质量,摆球只计质量不计大小,且摆线不伸缩,选项A、B、C正确。把单摆作为简谐运动来处理是有条件的,只有在摆角很小的情况下才能视单摆的运动为简谐运动,选项D错误。
ABC
4.下列关于单摆的说法正确的是( )
A. 单摆摆球从平衡位置运动到正向最大位移处时的位移为A(A为振幅),
从正向最大位移处运动到平衡位置时的位移为-A
B. 单摆摆球的回复力等于摆球所受的合外力
C. 单摆摆球的回复力等于摆球重力沿圆弧切线方向的分力
D. 单摆摆球经过平衡位置时加速度为零
解析:简谐运动中的位移是以平衡位置作为起点,摆球在正向最大位移处时位移为A,在平衡位置时位移应为零;摆球的回复力由重力沿圆弧切线方向的分力提供,线的拉力与重力沿摆线方向的分力的合力提供向心力;摆球经最低点(振动的平衡位置)时回复力为零,但向心力不为零,所以合外力不为零,加速度不为零。
C
5.将秒摆(周期为2 s的单摆)的周期变为4 s,下面哪些措施是正确的( )
A.只将摆球质量变为原来的
B.只将振幅变为原来的2倍
C.只将摆长变为原来的4倍
D.只将摆长变为原来的16倍
C
解析:单摆的周期与摆球的质量和振幅均无关,选项A、B错误;对该秒摆,T0=2π=2 s,对周期为4 s的单摆,T=2π=4 s,故l=4l0,故选项C正确,D错误。
本节内容结束
第二章 机械振动
3.单摆
教学目标
CONTENT
01
02
03
掌握单摆振动的周期公式
知道什么是单摆
会探究影响单摆周期公式的因素
生活中,我们常看到一些小振幅的摆动现象,类似简谐运动。
新课引入
当摆钟做小振幅的摆动时,可近似看作简谐运动,本节我们将在建立单摆模型的基础上,学习单摆摆动的规律
1.单摆:把一根不能伸长的细线上端固定,下端拴一个小球,线的质量和球的大小忽略不计,这种装置称为单摆。
2.理想化:
研究条件:与小球受到的重力及绳子的拉力相比,空气等对它的阻力可以忽略.
单摆的振动
一
知能提升
3.单摆的结构
θ
摆角
摆长:摆球重心到摆动圆弧圆心的距离。
偏角:摆到最高点时,细线与竖直方向的夹角。
摆线的长l0
摆长为l=l0+R
用什么方法探究单摆的振动是否为简谐运动?
1.位移与时间的关系是否满足正弦关系(x–t 图像法)
2.回复力与位移是否成正比且方向相反(F=-kx)
思考与讨论
B
A
O
方向:
沿切线指向平衡位置
P
θ
T
G
向心力大小:
与该点速度方向一致,不断改变速度大小
与该点速度方向垂直,只改变速度方向
方向:
沿半径指向悬点
理论推导:
摆球在任一点P点时,摆角为θ,摆球对O点的位移x,从O指向P
重力沿切线方向的分力提供回复力
P
O
θ
T
G
θ
F回=Mgsin θ
角度 弧度值θ sin θ
5° 0.08727 0.08716
4° 0.06981 0.06976
3° 0.05236 0.05234
2° 0.03491 0.03490
1° 0.01754 0.01754
当θ较小时,sinθ θ
位移方向与回复力方向相反F x
可以写成:F k x
结论:在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动。
一般偏角 F k x (k )
P
O
θ
T
G
θ
如图 ,细线下悬挂一个除去了柱塞的注射器,注射器内装上墨汁。当注射器摆动时,沿着垂直于摆动的方向匀速拖动木板,观察留在木板上的墨汁图样。
t
x
O
通过图像,可看出注射器的摆动是简谐运动
做一做
单摆的周期与哪些因素有关呢?
单摆的周期
二
知能提升
猜想:
1.与振幅有关
2.与摆球的质量有关
3.与摆长有关
思考与讨论
探究一:探究周期与振幅的关系
次数 1 2 3 4 5 6
20次全振动时间/s 37.72 37.78 37.82 37.65 37.83 37.84
周期/s 1.886 1.889 1.891 1.883 1.892 1.892
实验表明:单摆周期与振幅无关,这是摆的等时性。
做一做
探究二:探究周期与摆球质量的关系
实验思想:相同摆长,相同尺寸、不同质量的摆球。
实验表明:单摆周期与摆球质量无关
探究三:探究周期与摆长的关系
实验思想:改变摆长,重复多次实验,记录20个周期
数据记录如下表
实验次数 摆长cm 周期T(s) 20次周期(s)
1 30.95 1.12 22.32
5 49.90 1.42 28.34
9 76.95 1.76 35.15
10 82.75 1.82 36.44
13 93.95 1.95 38.98
16 109.45 2.10 41.98
19 135.95 2.34 46.78
1.单摆的周期与振幅无关——单摆的等时性。
2.单摆的周期与摆球的质量无关。
3.单摆的周期与摆长有关——摆长越长,周期越大。
【实验表明】
荷兰物理学家惠更斯(1629-1695)通过实验进一步得出:
单摆做简谐运动的周期跟摆长的算数平方根成正比,跟重力加速度的算数平方根成反比.
该式是个近似公式,由它算出的周期与精确值之间的差别随着偏角的增加而增加。当偏角为5 时两者相差0.01%
例.一个摆长为2 m的单摆,在地球上某地振动时,测得完成100次全振动所用的时间为284 s。
(1)求当地的重力加速度g的大小。
(2)把该单摆拿到月球上去,已知月球上的重力加速度是1.60 m/s2,则该单摆振动周期是多少
典例精析
解析: (1)周期T= s=2.84 s
由周期公式T=2π得,g= m/s2=9.78 m/s2。
(2)T'=2π=2×3.14× s=7.02 s。
一、单摆的振动:在小角度下,单摆是简谐运动
二、单摆的周期:
课堂小结
1.关于单摆摆球在运动过程中的受力,下列结论正确的是( )
A.摆球受重力、摆线的拉力作用
B.摆球受重力、摆线的拉力、回复力作用
C.摆球的回复力为零时,向心力最大
D.摆球的回复力最大时,摆线中的拉力大小比摆球的重力大
解析:单摆在运动过程中,摆球受重力和摆线的拉力,重力沿圆弧切线的分力提供回复力,故A对、B错;在平衡位置处,回复力为零,速度最大,向心力F向= 最大,选项C正确;当回复力最大时,摆球在最大位移处,速度为零,向心力为零,则拉力等于重力沿半径方向的分力,即拉力小于重力,选项D错误。
跟踪练习
AC
2.下列有关单摆运动过程中的受力,说法正确的是( )
A.单摆运动的回复力是重力和摆线拉力的合力
B.单摆运动的回复力是重力沿圆弧切线方向的分力
C.单摆经过平衡位置时合力为零
D.单摆运动的回复力是摆线拉力的一个分力
解析:单摆的回复力是重力沿圆弧切线方向的分力,故选项B正确,A、D错误;单摆经过平衡位置时,回复力为零,向心力最大,其合外力不为零,所以选项C错误。
B
3.(多选)单摆是为研究振动而抽象出的理想化模型,其理想化条件是( )
A.摆线质量不计
B.摆线长度不伸缩
C.摆球的直径比摆线长度短得多
D.只要是单摆的运动就是一种简谐运动
解析:单摆由摆线和摆球组成,摆线只计长度不计质量,摆球只计质量不计大小,且摆线不伸缩,选项A、B、C正确。把单摆作为简谐运动来处理是有条件的,只有在摆角很小的情况下才能视单摆的运动为简谐运动,选项D错误。
ABC
4.下列关于单摆的说法正确的是( )
A. 单摆摆球从平衡位置运动到正向最大位移处时的位移为A(A为振幅),
从正向最大位移处运动到平衡位置时的位移为-A
B. 单摆摆球的回复力等于摆球所受的合外力
C. 单摆摆球的回复力等于摆球重力沿圆弧切线方向的分力
D. 单摆摆球经过平衡位置时加速度为零
解析:简谐运动中的位移是以平衡位置作为起点,摆球在正向最大位移处时位移为A,在平衡位置时位移应为零;摆球的回复力由重力沿圆弧切线方向的分力提供,线的拉力与重力沿摆线方向的分力的合力提供向心力;摆球经最低点(振动的平衡位置)时回复力为零,但向心力不为零,所以合外力不为零,加速度不为零。
C
5.将秒摆(周期为2 s的单摆)的周期变为4 s,下面哪些措施是正确的( )
A.只将摆球质量变为原来的
B.只将振幅变为原来的2倍
C.只将摆长变为原来的4倍
D.只将摆长变为原来的16倍
C
解析:单摆的周期与摆球的质量和振幅均无关,选项A、B错误;对该秒摆,T0=2π=2 s,对周期为4 s的单摆,T=2π=4 s,故l=4l0,故选项C正确,D错误。
本节内容结束
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
