2023年中考宝安区数学备考冲刺题--模拟卷6(无答案)
文档属性
| 名称 | 2023年中考宝安区数学备考冲刺题--模拟卷6(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 813.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-27 16:47:25 | ||
图片预览

文档简介
2023年中考宝安区数学备考冲刺题--模拟卷6
一、选择题(每题3分,共30分)
1.剪纸艺术是我国非物质文化遗产,下列剪纸中,是中心对称图形的是( )
A. B. C. D.
2. 如图,该几何体的俯视图是( )
A. B. C. D.
3. 2022年,深圳学位建设扩容提质驶入“快车道”,新改扩建中小学校、幼儿园182所,新增基础教育学位20.6万个,再创历史新高.其中,20.6万用科学记数法表示为( )
2.06×105 B. 20.6×104 C. 2.06×104 D. 2.6×105
4.下列运算正确的是( )
A. B.
C. D.
5. 初一年级甲、乙两位同学参加“垃圾分类”知识竞赛,五次答题的得分情况如下:甲:7分,8分,8分,8分,9分;乙:6分,7分,8分,9分,10分.设甲的平均数和方差分别为,s2,乙的平均分和方差分别为1,,则下列正确的选项是( )
A.1 B. 1 C. s2> D. s2
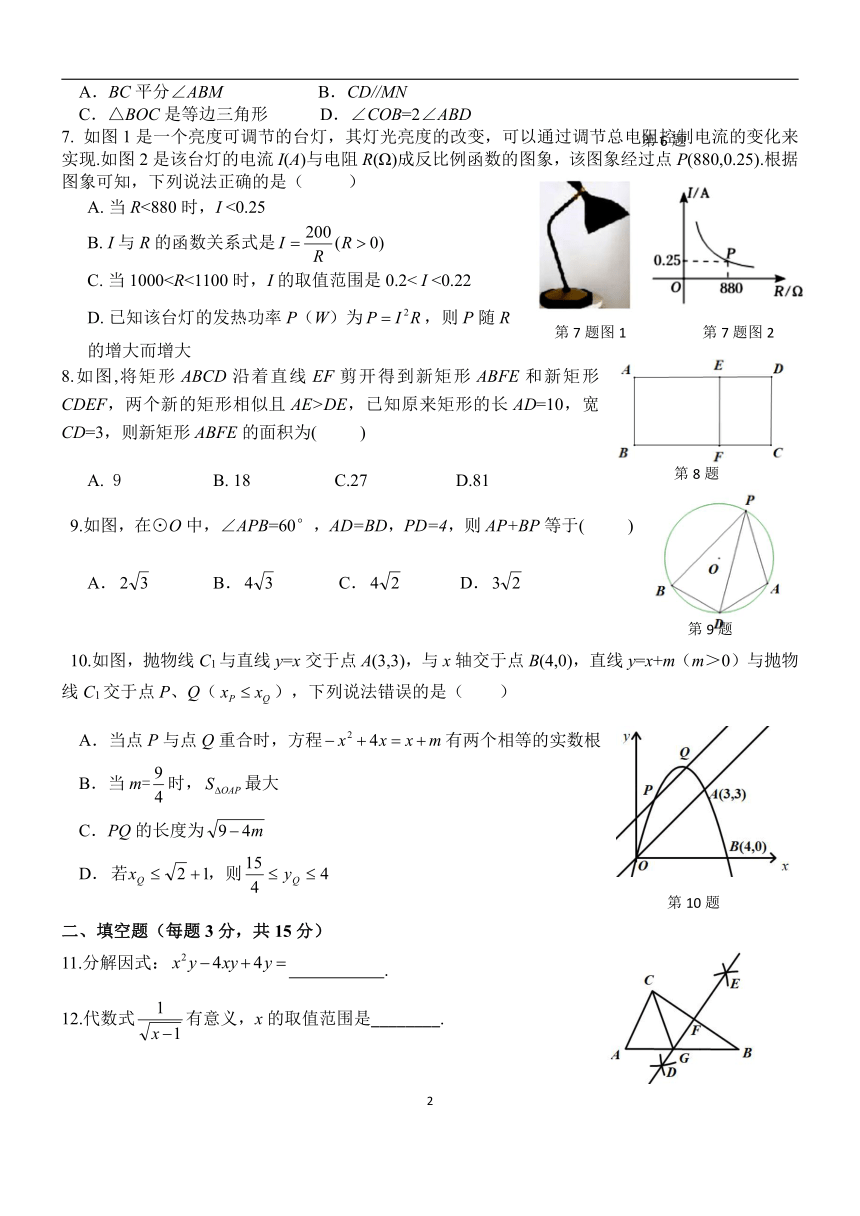
6. 如图,已知四边形ABCD是矩形,点B在直线MN上,若BD平分∠ABN,则下列结论不能推出的是( )
BC平分∠ABM B.CD//MN
C.△BOC是等边三角形 D.∠COB=2∠ABD
7. 如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流I(A)与电阻R(Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是( )
A. 当R<880时,I <0.25
B. I与R的函数关系式是
C. 当1000D. 已知该台灯的发热功率P(W)为,则P随R
的增大而增大
8.如图,将矩形ABCD沿着直线EF剪开得到新矩形ABFE和新矩形CDEF,两个新的矩形相似且AE>DE,已知原来矩形的长AD=10,宽CD=3,则新矩形ABFE的面积为( )
9 B. 18 C.27 D.81
9.如图,在⊙O中,∠APB=60°,AD=BD,PD=4,则AP+BP等于( )
A. B. C. D.
10.如图,抛物线C1与直线y=x交于点A(3,3),与x轴交于点B(4,0),直线y=x+m(m>0)与抛物线C1交于点P、Q(),下列说法错误的是( )
A.当点P与点Q重合时,方程有两个相等的实数根
B.当m=时,最大
C.PQ的长度为
D.
二、填空题(每题3分,共15分)
11.分解因式: .
12.代数式有意义,x的取值范围是________.
13.如图,在 △ABC中, 分别以点B和点C为圆心,大于BC 的长为半径作弧,两弧相交于D、E两点,作直线 DE交 BC于点 F,交 AB于点G,连接CG. 若AC=4,AB=5,则△ACG的周长为 .
14.在平面直角坐标系中,点A是反比例函数图象上的一点,如图,将线段OA向左平移,平移后的对应线段为O’A’,点A’落在反比例函数的图象上,已知线段OA扫过的面积为5,则k= .
15.(原创)如图,∠MON=90°,OM=ON=6,以点O为圆心,OM为半径作弧MN,点A是OM中点,点P是弧MN上的动点,以AP为直角边作Rt△APQ,且tan∠APQ=,连接NQ,则NQ的最小值为= .
三、解答题(共7题,第16题5分,第17题7分,第18题8分,第19题8分,第20题8分,第21题10分,第22题9分,共55分.)
16. 计算:
17.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,C2点坐标为 ;
(3)点P是y轴上的动点,当线段AP+BP的值最小时,点P的坐标为 .
18.为了响应市政府号召,某校开展了“文明城市与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“B”所在扇形的圆心角等于 度;
(4)小花和小华两名同学准备从中各自随机参加一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.
19. 2022年,第24届冬季奥林匹克运动会在北京和张家口举行,吉祥物冰墩墩和雪容融很受大家的欢迎.某超市以30元/盒购进一批冬奥会吉祥物礼盒,根据以往的销售经验得出以下的销售规律:每周销售量y(盒)和销售单价x(元)之间存在一次函数关系,如下表所示:
销售单价x(元) 35 40
销售量y(盒) 350 300
该超市规定,销售单价不低于每盒礼盒的进价,且利润率不高于60%.
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价定为多少元时,每周销售利润W(元)最大?最大利润为多少元
20.如图,AB为⊙O的直径,C为BA延长线上一点,D为⊙O上一点,OF⊥AD于点E,交CD于点F,且∠ADC=∠AOF.
(1)求证:CD与⊙O相切于点D;
(2)若AB=10,OE=4,求AC的长.
“湾区之光”摩天轮位于宝安区滨海文化公园内,是深圳上空最高的摩天轮,总高128米,有28个进口轿厢,每28分钟旋转一圈.如图是“湾区之光”摩天轮的示意图,转轮逆时针绕旋转中心O旋转,点O到地面的距离OB为h0米,转轮半径为R米.
小明坐在轿厢P内(近似看成一个点),点A是与旋转中心O点在同一水平线上的点(如图所示位置).某时,轿厢P达到A点处,摩天轮继续转动,记摩天轮转过的角度为(0°≤≤180°),设小明所在轿厢P距离地面的高度为h米,他想探究他离地面的高度h(米)与摩天轮旋转角度之间的函数关系.
(1)当=90°时,小明到达最高点,此时h= ;
当=0°或180°时,小明与点O同一水平线上,此时h=h0.
(2)当0°<<90°时,求h关于的函数关系式,并直接写出90°<<180°时,h关于的函数关系式.(h0、R为常数)
(3)若R=50米,h0=78米,小明尝试画出h关于的函数图象.
①列表:
0° 30° 45° 60° 90° 120° 135° 150° 180°
h(米) 78 103 113 128 121 103 78
请你将上表补充完整(结果保留整数,)
②描点、连线:
请描出剩下的两个点,并用光滑曲线顺次连接所有点,画出h关于函数的大致图象.
③观察图象,请写出该函数图象的一条性质: .
(4)若R=52米,h0=80米,小明从轿厢P达到A点开始计时,经过 分钟后,他距离地面高度为106米.
问题背景:如图1,已知AP平分△ABC的内角∠A,过点B作BD∥AC,与AP的延长线交于点D.延长AC到点F,使得AF=BD.
证明:四边形ABDF是菱形;
探究发现:(2)数学兴趣小组有同学发现在上面图形中:已知AP平分△ABC的内角∠A,则AB:BP=AC:CP.该同学通过证明得出结论:三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例.请你利用图1证明这一结论.
拓展运用:(3)兴趣小组的其他成员将△ABC沿着直线BC进行折叠,使得点A刚好落在四边形ABCD的另一对角线BF上,记折叠后点A的对应点为点A’,如图2,若OA=4,OB=3.
①求A’P的长;
②△A’PC的面积为 .
第6题
第7题图1 第7题图2
第8题
第9题
第10题
第13题
第15题
第14题
第17题
第18题
第20题
第22题图1
第22题图2
一、选择题(每题3分,共30分)
1.剪纸艺术是我国非物质文化遗产,下列剪纸中,是中心对称图形的是( )
A. B. C. D.
2. 如图,该几何体的俯视图是( )
A. B. C. D.
3. 2022年,深圳学位建设扩容提质驶入“快车道”,新改扩建中小学校、幼儿园182所,新增基础教育学位20.6万个,再创历史新高.其中,20.6万用科学记数法表示为( )
2.06×105 B. 20.6×104 C. 2.06×104 D. 2.6×105
4.下列运算正确的是( )
A. B.
C. D.
5. 初一年级甲、乙两位同学参加“垃圾分类”知识竞赛,五次答题的得分情况如下:甲:7分,8分,8分,8分,9分;乙:6分,7分,8分,9分,10分.设甲的平均数和方差分别为,s2,乙的平均分和方差分别为1,,则下列正确的选项是( )
A.1 B. 1 C. s2> D. s2
6. 如图,已知四边形ABCD是矩形,点B在直线MN上,若BD平分∠ABN,则下列结论不能推出的是( )
BC平分∠ABM B.CD//MN
C.△BOC是等边三角形 D.∠COB=2∠ABD
7. 如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流I(A)与电阻R(Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是( )
A. 当R<880时,I <0.25
B. I与R的函数关系式是
C. 当1000
的增大而增大
8.如图,将矩形ABCD沿着直线EF剪开得到新矩形ABFE和新矩形CDEF,两个新的矩形相似且AE>DE,已知原来矩形的长AD=10,宽CD=3,则新矩形ABFE的面积为( )
9 B. 18 C.27 D.81
9.如图,在⊙O中,∠APB=60°,AD=BD,PD=4,则AP+BP等于( )
A. B. C. D.
10.如图,抛物线C1与直线y=x交于点A(3,3),与x轴交于点B(4,0),直线y=x+m(m>0)与抛物线C1交于点P、Q(),下列说法错误的是( )
A.当点P与点Q重合时,方程有两个相等的实数根
B.当m=时,最大
C.PQ的长度为
D.
二、填空题(每题3分,共15分)
11.分解因式: .
12.代数式有意义,x的取值范围是________.
13.如图,在 △ABC中, 分别以点B和点C为圆心,大于BC 的长为半径作弧,两弧相交于D、E两点,作直线 DE交 BC于点 F,交 AB于点G,连接CG. 若AC=4,AB=5,则△ACG的周长为 .
14.在平面直角坐标系中,点A是反比例函数图象上的一点,如图,将线段OA向左平移,平移后的对应线段为O’A’,点A’落在反比例函数的图象上,已知线段OA扫过的面积为5,则k= .
15.(原创)如图,∠MON=90°,OM=ON=6,以点O为圆心,OM为半径作弧MN,点A是OM中点,点P是弧MN上的动点,以AP为直角边作Rt△APQ,且tan∠APQ=,连接NQ,则NQ的最小值为= .
三、解答题(共7题,第16题5分,第17题7分,第18题8分,第19题8分,第20题8分,第21题10分,第22题9分,共55分.)
16. 计算:
17.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,C2点坐标为 ;
(3)点P是y轴上的动点,当线段AP+BP的值最小时,点P的坐标为 .
18.为了响应市政府号召,某校开展了“文明城市与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“B”所在扇形的圆心角等于 度;
(4)小花和小华两名同学准备从中各自随机参加一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.
19. 2022年,第24届冬季奥林匹克运动会在北京和张家口举行,吉祥物冰墩墩和雪容融很受大家的欢迎.某超市以30元/盒购进一批冬奥会吉祥物礼盒,根据以往的销售经验得出以下的销售规律:每周销售量y(盒)和销售单价x(元)之间存在一次函数关系,如下表所示:
销售单价x(元) 35 40
销售量y(盒) 350 300
该超市规定,销售单价不低于每盒礼盒的进价,且利润率不高于60%.
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价定为多少元时,每周销售利润W(元)最大?最大利润为多少元
20.如图,AB为⊙O的直径,C为BA延长线上一点,D为⊙O上一点,OF⊥AD于点E,交CD于点F,且∠ADC=∠AOF.
(1)求证:CD与⊙O相切于点D;
(2)若AB=10,OE=4,求AC的长.
“湾区之光”摩天轮位于宝安区滨海文化公园内,是深圳上空最高的摩天轮,总高128米,有28个进口轿厢,每28分钟旋转一圈.如图是“湾区之光”摩天轮的示意图,转轮逆时针绕旋转中心O旋转,点O到地面的距离OB为h0米,转轮半径为R米.
小明坐在轿厢P内(近似看成一个点),点A是与旋转中心O点在同一水平线上的点(如图所示位置).某时,轿厢P达到A点处,摩天轮继续转动,记摩天轮转过的角度为(0°≤≤180°),设小明所在轿厢P距离地面的高度为h米,他想探究他离地面的高度h(米)与摩天轮旋转角度之间的函数关系.
(1)当=90°时,小明到达最高点,此时h= ;
当=0°或180°时,小明与点O同一水平线上,此时h=h0.
(2)当0°<<90°时,求h关于的函数关系式,并直接写出90°<<180°时,h关于的函数关系式.(h0、R为常数)
(3)若R=50米,h0=78米,小明尝试画出h关于的函数图象.
①列表:
0° 30° 45° 60° 90° 120° 135° 150° 180°
h(米) 78 103 113 128 121 103 78
请你将上表补充完整(结果保留整数,)
②描点、连线:
请描出剩下的两个点,并用光滑曲线顺次连接所有点,画出h关于函数的大致图象.
③观察图象,请写出该函数图象的一条性质: .
(4)若R=52米,h0=80米,小明从轿厢P达到A点开始计时,经过 分钟后,他距离地面高度为106米.
问题背景:如图1,已知AP平分△ABC的内角∠A,过点B作BD∥AC,与AP的延长线交于点D.延长AC到点F,使得AF=BD.
证明:四边形ABDF是菱形;
探究发现:(2)数学兴趣小组有同学发现在上面图形中:已知AP平分△ABC的内角∠A,则AB:BP=AC:CP.该同学通过证明得出结论:三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例.请你利用图1证明这一结论.
拓展运用:(3)兴趣小组的其他成员将△ABC沿着直线BC进行折叠,使得点A刚好落在四边形ABCD的另一对角线BF上,记折叠后点A的对应点为点A’,如图2,若OA=4,OB=3.
①求A’P的长;
②△A’PC的面积为 .
第6题
第7题图1 第7题图2
第8题
第9题
第10题
第13题
第15题
第14题
第17题
第18题
第20题
第22题图1
第22题图2
同课章节目录
