2022~2023学年湘教版数学八年级下册期末测试卷(含答案)
文档属性
| 名称 | 2022~2023学年湘教版数学八年级下册期末测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 359.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-27 20:25:07 | ||
图片预览


文档简介
2022~2023学年湘教版数学八年级下册期末测试卷
一、选择题(共12题,共36分)
下列各组数中,以 ,, 为边的三角形不是直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
在平行四边形 中, 比 大 ,那么 的度数为
A. B. C. D.
如图,三个正方形围成一个直角三角形, 、 分别为所在正方形的面积,则图中字母 所代表的正方形面积是
A. B. C. D.
如图,在直角三角形 中,,,,点 为 的中点,点 在 上,且 于 ,则
A. B. C. D.
如图,矩形 的边 长为 ,边 长为 , 在数轴上,以原点 为圆心,对角线 的长为半径画弧,交正半轴于一点,则这个点表示的实数是
A. B. C. D.
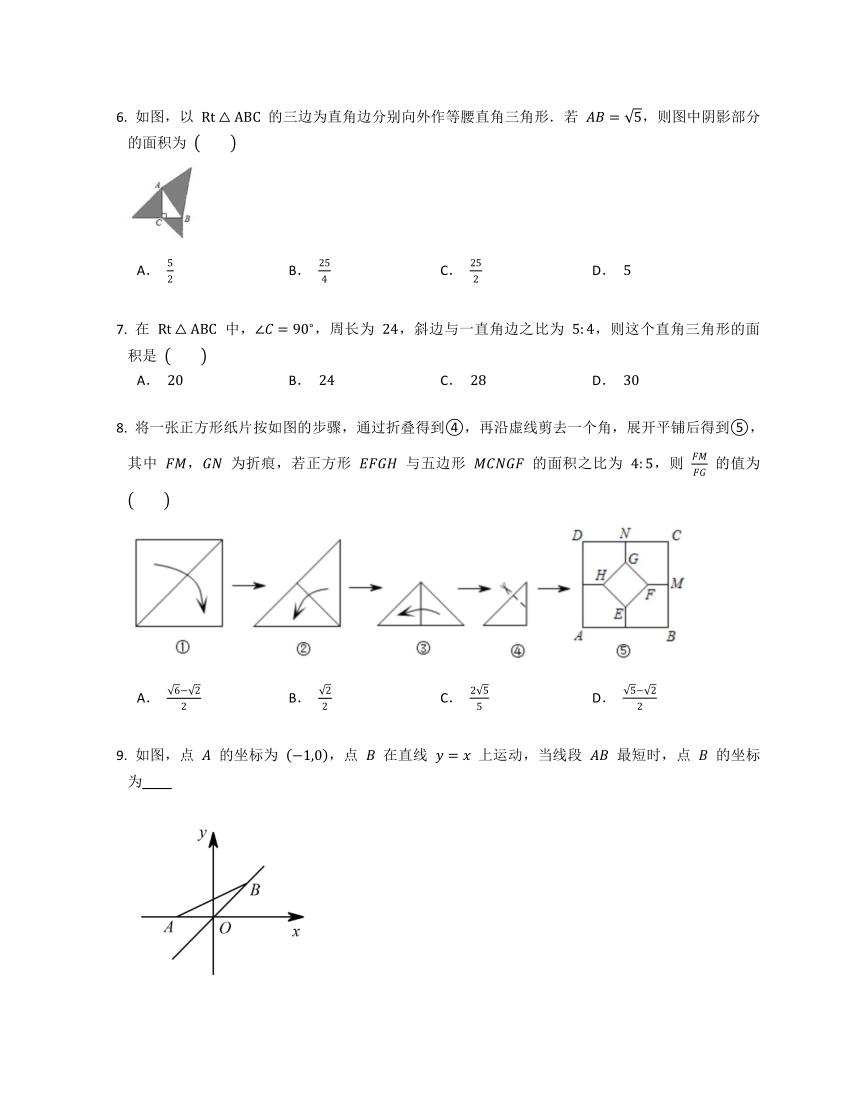
如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为
A. B. C. D.
在 中,,周长为 ,斜边与一直角边之比为 ,则这个直角三角形的面积是
A. B. C. D.
将一张正方形纸片按如图的步骤,通过折叠得到④,再沿虚线剪去一个角,展开平铺后得到⑤,其中 , 为折痕,若正方形 与五边形 的面积之比为 ,则 的值为
A. B. C. D.
如图,点 的坐标为 ,点 在直线 上运动,当线段 最短时,点 的坐标为
A. B.
C. D.
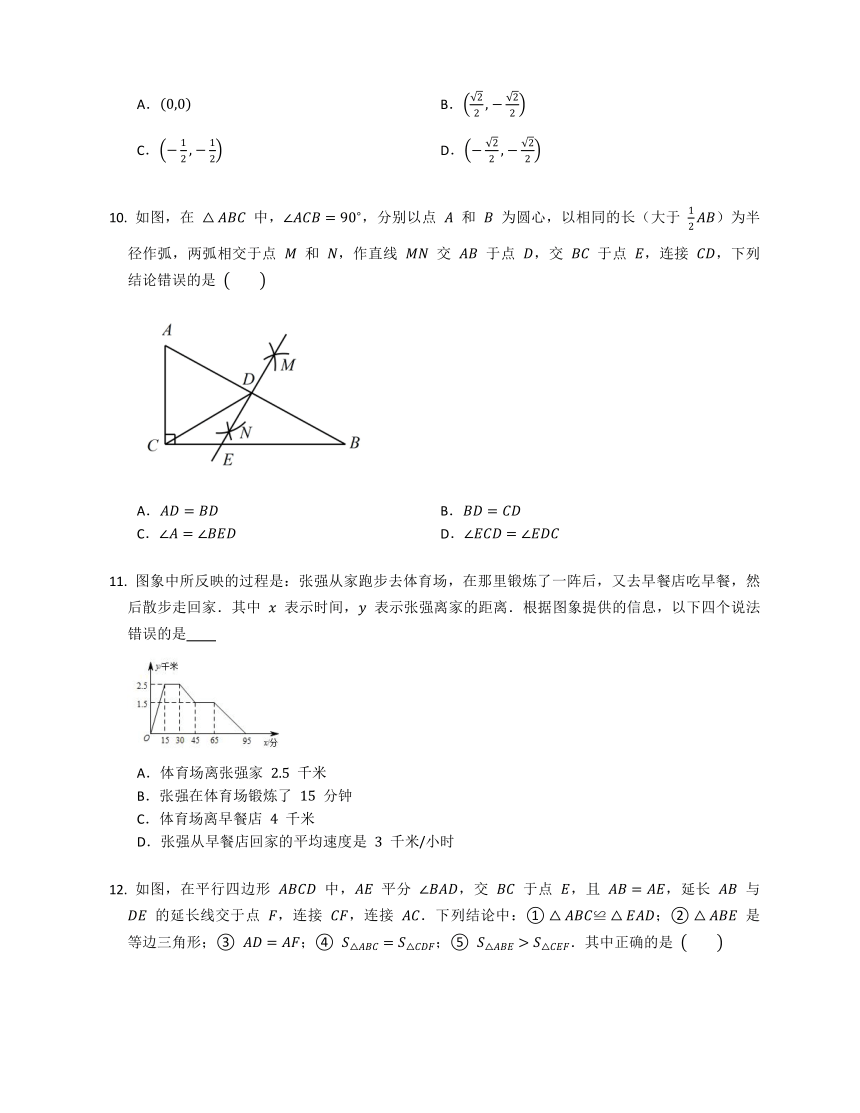
如图,在 中,,分别以点 和 为圆心,以相同的长(大于 )为半径作弧,两弧相交于点 和 ,作直线 交 于点 ,交 于点 ,连接 ,下列结论错误的是
A. B.
C. D.
图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中 表示时间, 表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是
A.体育场离张强家 千米
B.张强在体育场锻炼了 分钟
C.体育场离早餐店 千米
D.张强从早餐店回家的平均速度是 千米/小时
如图,在平行四边形 中, 平分 ,交 于点 ,且 ,延长 与 的延长线交于点 ,连接 ,连接 .下列结论中:① ;② 是等边三角形;③ ;④ ;⑤ .其中正确的是
A.②③⑤ B.①④⑤ C.①②③ D.①②④
二、填空题(共4题,共8分)
如图,已知四边形 中,,,,,,则四边形 的面积等于 .
如图所示,在四边形 中,,,,则 的度数为 度.
如图,在 中,,点 是边 上一点,点 , 分别是 , 的中点.若 ,,,则 的周长是 .
如图,在平面直角坐标系中,点 的坐标为 ,以 为直角边作 ,并使 ,再以 为直角边作 ,并使 ,再以 为直角边作 ,并使 , 按此规律进行下去,则点 的坐标为 .
三、解答题(共8题,共56分)
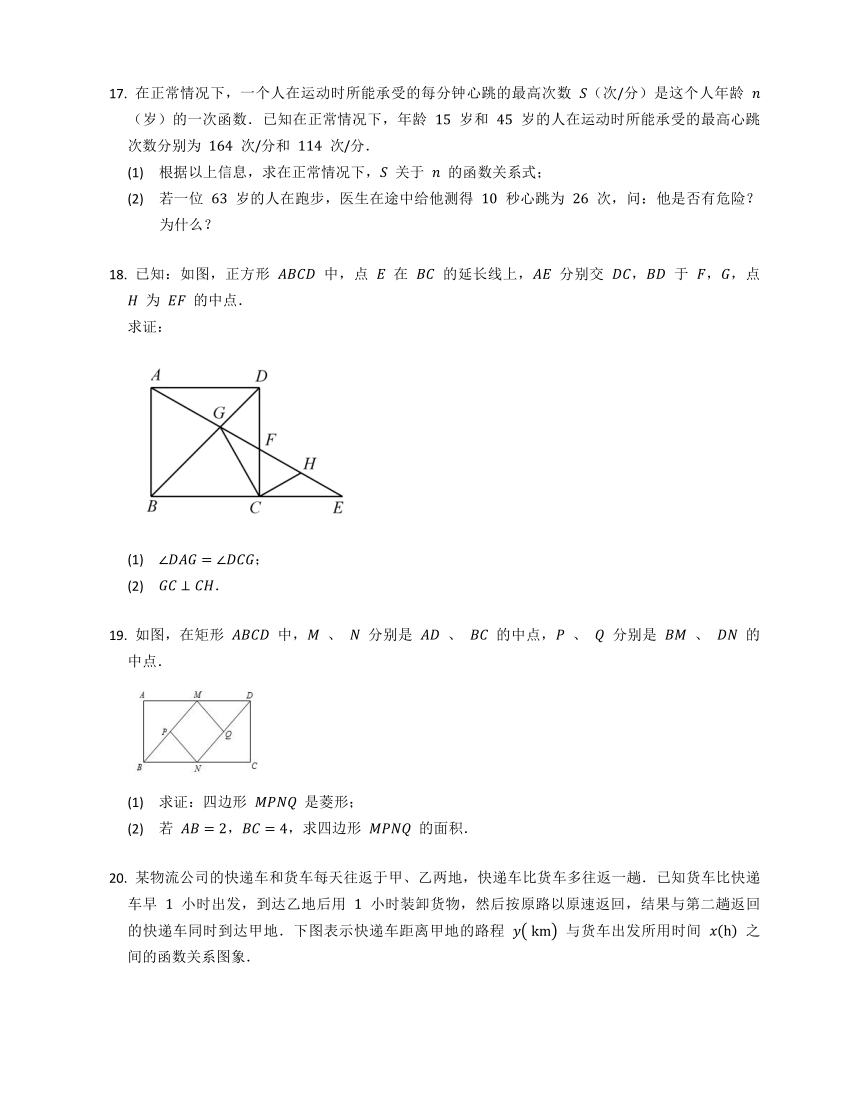
在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数 (次/分)是这个人年龄 (岁)的一次函数.已知在正常情况下,年龄 岁和 岁的人在运动时所能承受的最高心跳次数分别为 次/分和 次/分.
(1) 根据以上信息,求在正常情况下, 关于 的函数关系式;
(2) 若一位 岁的人在跑步,医生在途中给他测得 秒心跳为 次,问:他是否有危险?为什么?
已知:如图,正方形 中,点 在 的延长线上, 分别交 , 于 ,,点 为 的中点.
求证:
(1) ;
(2) .
如图,在矩形 中, 、 分别是 、 的中点, 、 分别是 、 的中点.
(1) 求证:四边形 是菱形;
(2) 若 ,,求四边形 的面积.
某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多往返一趟.已知货车比快递车早 小时出发,到达乙地后用 小时装卸货物,然后按原路以原速返回,结果与第二趟返回的快递车同时到达甲地.下图表示快递车距离甲地的路程 与货车出发所用时间 之间的函数关系图象.
(1) (1)请在下图中画出货车距离甲地的路程 与所用时间 的函数关系图象;
(2)两车在中途相遇 次.
(2) 试求货车从乙地返回甲地时 与所用时间 的函数关系式.
(3) 求快递车第二次从甲地出发到与返程货车相遇所用时间为多少 ?这时货车离乙地多少 ?
如图所示, 在正方形网格中,若点 的坐标为 ,按要求回答下列问题:
(1) 在图中建立正确的平面直角坐标系;
(2) 根据所建立的坐标系,写出点 和点 的坐标;
(3) 作出 关于 轴的对称图形 .(不用写作法)
(4) 求 的面积.
某社区计划对面积为 的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队 天能完成绿化的面积等于乙队 天完成绿化的面积,甲队 天能完成绿化的面积比乙队 天能完成绿化面积多 .
(1) 求甲、乙两工程队每天能完成绿化的面积.
(2) 设甲工程队施工 天,乙工程队施工 天,刚好完成绿化任务,求 与 的函数解析式.
(3) 若甲队每天绿化费用是 万元,乙队每天绿化费用为 万元,且乙队最少施工 天,最多施工 天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
如图,菱形 中,点 是 的中点,,射线 交 的延长线于点 ,射线 交 于点 ,点 是线段 的中点.
(1) 求证:;
(2) 若 ,试求出 的值;
(3) 作 于点 ,作 于点 ,连接 ,,如图 所示,请证明 是等腰三角形,并直接写出 的度数.
两个全等的直角三角形重叠放在直线 上,如图 1,,,,将 在直线 上左右平移,如图 2 所示.
(1) 求证:四边形 是平行四边形;
(2) 怎样移动 ,使得四边形 为菱形;
(3) 将 向左平移 ,求四边形 的面积.
答案
一、选择题(共12题)
1. 【答案】C
2. 【答案】D
3. 【答案】A
4. 【答案】C
5. 【答案】D
6. 【答案】D
7. 【答案】B
8. 【答案】A
9. 【答案】C
10. 【答案】D
11. 【答案】C
12. 【答案】D
二、填空题(共4题)
13. 【答案】
14. 【答案】
15. 【答案】
16. 【答案】
三、解答题(共8题)
17. 【答案】
(1) 设 关于 的函数关系式为 .由题设得解得所以 关于 的函数关系式为 .
(2) 当 时,.
因为这位 岁的人 秒心跳为 次,所以每分钟心跳为 次,
因此他不适合从事如此剧烈的运动,他有危险.
18. 【答案】
(1) 为正方形,
,,.
又 ,
.
.
(2) 为正方形,
.
.
又 ,
.
为直角三角形 斜边 边的中点,
.
.
.
又 ,
,即 .
.
19. 【答案】
(1) 四边形 是矩形,
,,
、 分别 、 的中点,
,
四边形 是平行四边形,
,,
、 分别 、 的中点,
,,
四边形 是平行四边形,
连接 ,
四边形 是矩形,
,,
、 分别 、 的中点,
,
四边形 是矩形,
,
是 中点,
,
四边形 是菱形.
(2) ,, 为 中点, 为 中点,
平行四边形 的面积是 ,
的面积是 ,
的面积是 ,
同理 的面积是 ,
四边形 的面积是 .
20. 【答案】
(1) 由题意得,货车从甲地到达乙地的时间为 小时,
所以,从 小时到 小时 , 小时时 ,
作函数图象如图所示:
(2)两车在中途相遇 次;
(2) 设 (),
函数图象经过点 ,,
代入得
解得
.
(3) 设快递车第二次从甲地出发的函数解析式为 (),
则
解得
,
联立
解得
小时,
,
答:快递车第二次从甲地出发到与返程货车相遇所用时间为 小时,这时货车离乙地 .
21. 【答案】
(1) 所建立的平面直角坐标系略
(2) 点 和点 的坐标分别为:,.
(3) 所作 如图所示.
(4)
22. 【答案】
(1) 甲每天完成 ,乙每天完成 .
(2) .
(3) 甲施工 ,乙施工 天,最低费用为 万元.
23. 【答案】
(1) 四边形 为菱形,
,
,,
在 和 中,
.
(2) 如图 ,作 交 于 ,
则 ,又点 是 的中点,
,
,
,
,
,
.
(3) 如图 ,作 于 ,
于 , 于 ,
,
点 是线段 的中点,
,又 ,
,
即 是等腰三角形,
由题意得,,, 为直角三角形,
设 ,则 ,由勾股定理得,,
则 .
根据三角形面积公式,,
由 得,,
,
,
,
,
的度数为 .
24. 【答案】
(1) ,
,,
,
四边形 是平行四边形.
(2) 在 中,由勾股定理得 ,要使四边形 为菱形,则 ,
可将 向左平移 或向右平移 .
(3) 在 中,.
当 向左平移 时,,
在 中,.
四边形 的面积为 .
一、选择题(共12题,共36分)
下列各组数中,以 ,, 为边的三角形不是直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
在平行四边形 中, 比 大 ,那么 的度数为
A. B. C. D.
如图,三个正方形围成一个直角三角形, 、 分别为所在正方形的面积,则图中字母 所代表的正方形面积是
A. B. C. D.
如图,在直角三角形 中,,,,点 为 的中点,点 在 上,且 于 ,则
A. B. C. D.
如图,矩形 的边 长为 ,边 长为 , 在数轴上,以原点 为圆心,对角线 的长为半径画弧,交正半轴于一点,则这个点表示的实数是
A. B. C. D.
如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为
A. B. C. D.
在 中,,周长为 ,斜边与一直角边之比为 ,则这个直角三角形的面积是
A. B. C. D.
将一张正方形纸片按如图的步骤,通过折叠得到④,再沿虚线剪去一个角,展开平铺后得到⑤,其中 , 为折痕,若正方形 与五边形 的面积之比为 ,则 的值为
A. B. C. D.
如图,点 的坐标为 ,点 在直线 上运动,当线段 最短时,点 的坐标为
A. B.
C. D.
如图,在 中,,分别以点 和 为圆心,以相同的长(大于 )为半径作弧,两弧相交于点 和 ,作直线 交 于点 ,交 于点 ,连接 ,下列结论错误的是
A. B.
C. D.
图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中 表示时间, 表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是
A.体育场离张强家 千米
B.张强在体育场锻炼了 分钟
C.体育场离早餐店 千米
D.张强从早餐店回家的平均速度是 千米/小时
如图,在平行四边形 中, 平分 ,交 于点 ,且 ,延长 与 的延长线交于点 ,连接 ,连接 .下列结论中:① ;② 是等边三角形;③ ;④ ;⑤ .其中正确的是
A.②③⑤ B.①④⑤ C.①②③ D.①②④
二、填空题(共4题,共8分)
如图,已知四边形 中,,,,,,则四边形 的面积等于 .
如图所示,在四边形 中,,,,则 的度数为 度.
如图,在 中,,点 是边 上一点,点 , 分别是 , 的中点.若 ,,,则 的周长是 .
如图,在平面直角坐标系中,点 的坐标为 ,以 为直角边作 ,并使 ,再以 为直角边作 ,并使 ,再以 为直角边作 ,并使 , 按此规律进行下去,则点 的坐标为 .
三、解答题(共8题,共56分)
在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数 (次/分)是这个人年龄 (岁)的一次函数.已知在正常情况下,年龄 岁和 岁的人在运动时所能承受的最高心跳次数分别为 次/分和 次/分.
(1) 根据以上信息,求在正常情况下, 关于 的函数关系式;
(2) 若一位 岁的人在跑步,医生在途中给他测得 秒心跳为 次,问:他是否有危险?为什么?
已知:如图,正方形 中,点 在 的延长线上, 分别交 , 于 ,,点 为 的中点.
求证:
(1) ;
(2) .
如图,在矩形 中, 、 分别是 、 的中点, 、 分别是 、 的中点.
(1) 求证:四边形 是菱形;
(2) 若 ,,求四边形 的面积.
某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多往返一趟.已知货车比快递车早 小时出发,到达乙地后用 小时装卸货物,然后按原路以原速返回,结果与第二趟返回的快递车同时到达甲地.下图表示快递车距离甲地的路程 与货车出发所用时间 之间的函数关系图象.
(1) (1)请在下图中画出货车距离甲地的路程 与所用时间 的函数关系图象;
(2)两车在中途相遇 次.
(2) 试求货车从乙地返回甲地时 与所用时间 的函数关系式.
(3) 求快递车第二次从甲地出发到与返程货车相遇所用时间为多少 ?这时货车离乙地多少 ?
如图所示, 在正方形网格中,若点 的坐标为 ,按要求回答下列问题:
(1) 在图中建立正确的平面直角坐标系;
(2) 根据所建立的坐标系,写出点 和点 的坐标;
(3) 作出 关于 轴的对称图形 .(不用写作法)
(4) 求 的面积.
某社区计划对面积为 的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队 天能完成绿化的面积等于乙队 天完成绿化的面积,甲队 天能完成绿化的面积比乙队 天能完成绿化面积多 .
(1) 求甲、乙两工程队每天能完成绿化的面积.
(2) 设甲工程队施工 天,乙工程队施工 天,刚好完成绿化任务,求 与 的函数解析式.
(3) 若甲队每天绿化费用是 万元,乙队每天绿化费用为 万元,且乙队最少施工 天,最多施工 天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
如图,菱形 中,点 是 的中点,,射线 交 的延长线于点 ,射线 交 于点 ,点 是线段 的中点.
(1) 求证:;
(2) 若 ,试求出 的值;
(3) 作 于点 ,作 于点 ,连接 ,,如图 所示,请证明 是等腰三角形,并直接写出 的度数.
两个全等的直角三角形重叠放在直线 上,如图 1,,,,将 在直线 上左右平移,如图 2 所示.
(1) 求证:四边形 是平行四边形;
(2) 怎样移动 ,使得四边形 为菱形;
(3) 将 向左平移 ,求四边形 的面积.
答案
一、选择题(共12题)
1. 【答案】C
2. 【答案】D
3. 【答案】A
4. 【答案】C
5. 【答案】D
6. 【答案】D
7. 【答案】B
8. 【答案】A
9. 【答案】C
10. 【答案】D
11. 【答案】C
12. 【答案】D
二、填空题(共4题)
13. 【答案】
14. 【答案】
15. 【答案】
16. 【答案】
三、解答题(共8题)
17. 【答案】
(1) 设 关于 的函数关系式为 .由题设得解得所以 关于 的函数关系式为 .
(2) 当 时,.
因为这位 岁的人 秒心跳为 次,所以每分钟心跳为 次,
因此他不适合从事如此剧烈的运动,他有危险.
18. 【答案】
(1) 为正方形,
,,.
又 ,
.
.
(2) 为正方形,
.
.
又 ,
.
为直角三角形 斜边 边的中点,
.
.
.
又 ,
,即 .
.
19. 【答案】
(1) 四边形 是矩形,
,,
、 分别 、 的中点,
,
四边形 是平行四边形,
,,
、 分别 、 的中点,
,,
四边形 是平行四边形,
连接 ,
四边形 是矩形,
,,
、 分别 、 的中点,
,
四边形 是矩形,
,
是 中点,
,
四边形 是菱形.
(2) ,, 为 中点, 为 中点,
平行四边形 的面积是 ,
的面积是 ,
的面积是 ,
同理 的面积是 ,
四边形 的面积是 .
20. 【答案】
(1) 由题意得,货车从甲地到达乙地的时间为 小时,
所以,从 小时到 小时 , 小时时 ,
作函数图象如图所示:
(2)两车在中途相遇 次;
(2) 设 (),
函数图象经过点 ,,
代入得
解得
.
(3) 设快递车第二次从甲地出发的函数解析式为 (),
则
解得
,
联立
解得
小时,
,
答:快递车第二次从甲地出发到与返程货车相遇所用时间为 小时,这时货车离乙地 .
21. 【答案】
(1) 所建立的平面直角坐标系略
(2) 点 和点 的坐标分别为:,.
(3) 所作 如图所示.
(4)
22. 【答案】
(1) 甲每天完成 ,乙每天完成 .
(2) .
(3) 甲施工 ,乙施工 天,最低费用为 万元.
23. 【答案】
(1) 四边形 为菱形,
,
,,
在 和 中,
.
(2) 如图 ,作 交 于 ,
则 ,又点 是 的中点,
,
,
,
,
,
.
(3) 如图 ,作 于 ,
于 , 于 ,
,
点 是线段 的中点,
,又 ,
,
即 是等腰三角形,
由题意得,,, 为直角三角形,
设 ,则 ,由勾股定理得,,
则 .
根据三角形面积公式,,
由 得,,
,
,
,
,
的度数为 .
24. 【答案】
(1) ,
,,
,
四边形 是平行四边形.
(2) 在 中,由勾股定理得 ,要使四边形 为菱形,则 ,
可将 向左平移 或向右平移 .
(3) 在 中,.
当 向左平移 时,,
在 中,.
四边形 的面积为 .
同课章节目录
