10.4 中心对称 学案
图片预览




文档简介
中小学教育资源及组卷应用平台
10.4 中心对称 导学案
课题 10.4 中心对称 单元 第10单元 学科 数学 年级 七年级(下)
教材分析 通过观察、探究了解两个图形关于一点成中心对称的概念,知道中心对称图形和中心对称两者之间的关系.
核心素养分析 通过对中心对称性质的认识,提高分析、归纳、猜想、证明等能力,体会化归、数形结合等数学思想;提高合情推理能力,培养数学说理的习惯与能力,感受数学图形的对称美.
学习目标 1、知道中心对称与中心对称图形的意义.2、知道成中心对称的两个图形的性质,会判断两个图形是否成中心对称,会画一个图形关于一个点成中心对称的图形.
重点 对中心对称的理解与中心对称性质的掌握.
难点 中心对称与轴对称的区别与联系.
教学过程
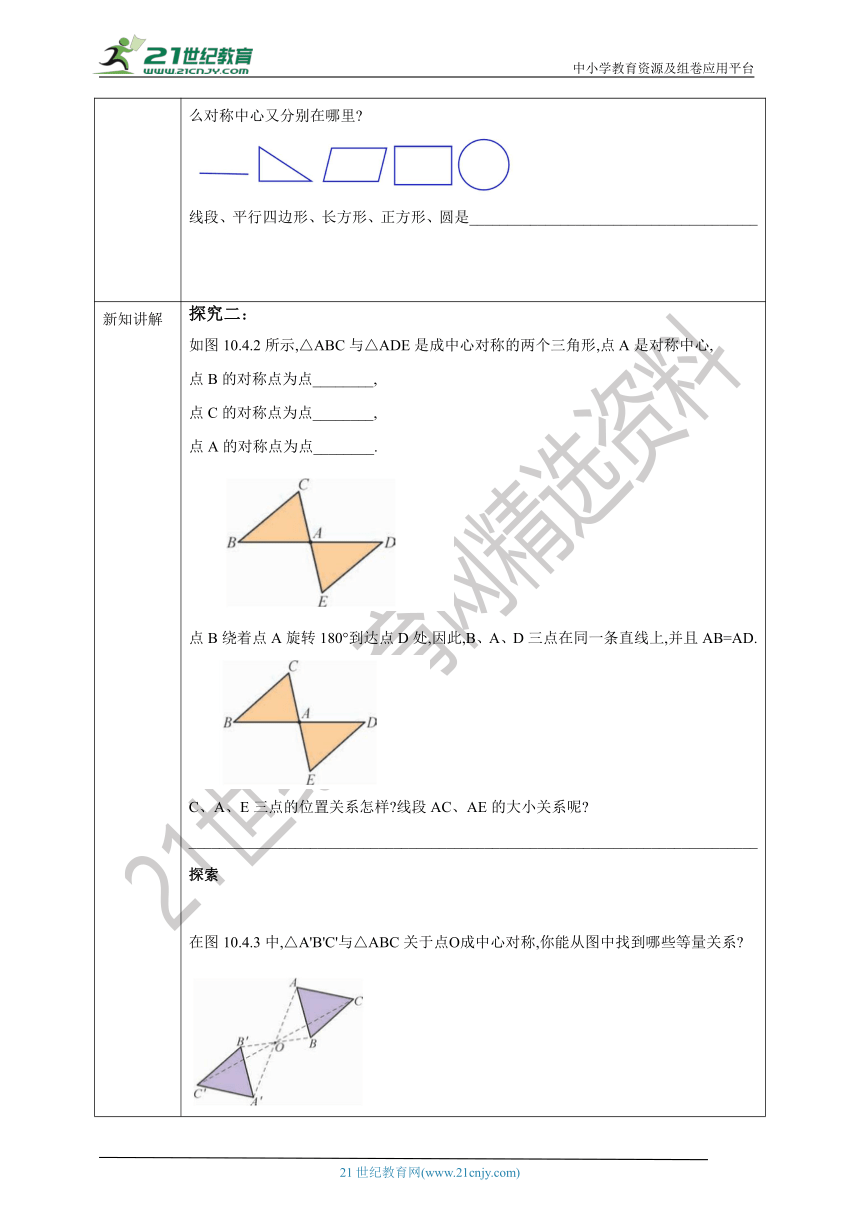
课前预学 引入思考探究一:在上一节,我们已经看到有不少图形绕某一中心旋转一定角度后,可以与自身重合.如图所示的三个图形都是这样的旋转对称图形.归纳:一个图形绕着中心旋转 后能与自身重合,把这样的图形叫做中心对称图形,这个中心叫做 .2、把一个图形绕着某一点旋转 ,如果它能够和 重合,那么,我们就说这两个图形成中心对称。3、中心对称和中心对称图形是一个概念吗?4、如何确定成中心对称的两个图形的对称中心?想一想 线段、三角形、平行四边形、长方形、正方形、圆分别是中心对称图形吗 如果是,那么对称中心又分别在哪里 线段、平行四边形、长方形、正方形、圆是______________________________________
新知讲解 探究二:如图10.4.2所示,△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,点B的对称点为点________,点C的对称点为点________,点A的对称点为点________.点B绕着点A旋转180°到达点D处,因此,B、A、D三点在同一条直线上,并且AB=AD.A、E三点的位置关系怎样 线段AC、AE的大小关系呢 ___________________________________________________________________________探索在图10.4.3中,△A'B'C'与△ABC关于点О成中心对称,你能从图中找到哪些等量关系 提炼概念归纳总结:性质:成中心对称的两个图形,对称点的连线都经过对称中心,且被对称中心平分.判定:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称. 典例精讲 例:如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.试一试如图10.4.6所示的两个图形成中心对称,你能找到它们的对称中心吗 小明找到了如图10.4.7所示的方法,你呢 你知道其中的理由吗 你还能找到其他的方法吗
课堂练习 巩固训练1.对如图的对称性表述,正确的是( )轴对称图形
B. 中心对称图形
C. 既是轴对称图形又是中心对称图形
D. 既不是轴对称图形又不是中心对称图形
2.下列说法中,错误的是( )A.成中心对称的两个图形面积相等B.成中心对称的两个图形中,对称点的连线被对称轴平分C.中心对称图形的对称中心是对称点连线的中心D.中心对称图形绕对称中心旋转180°后,都能与自身重合3.如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为________.4.观察图形,并回答下面的问题:(1)哪些是轴对称图形?(2)哪些是中心对称图形?(3)哪些既是中心对称图形,又是轴对称图形?(4)哪些既不是中心对称图形,又不是轴对称图形?5.如图,在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 求对称中心E点的坐标.6.如图,△ABO与△CDO关于点O成中心对称,点E,F在线段AC上,且AF=CE,试说明FD=BE.答案引入思考探究一:把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称,想一想:线段的对称中心是线段的中点平行四边形、长方形、正方形的对称中心是它们对角线的交点,圆的对称中心是圆心。探究二:我们可以发现,点A 绕中心点О旋转180°后到点A',于是A、O、A'三点在同一条直线上,并且OA=OA'.另外分别在同一条直线上的三点还有B、O、B'和C、O、C';并且OB=OB',OC=OC'点B的对称点为点D ,点C的对称点为点 E,点A的对称点为点 A.点B绕着点A旋转180°到达点D处,因此,B、A、D三点在同一条直线上,并且AB=AD.C、A、E三点的位置关系怎样 线段AC、AE的大小关系呢 C、A、E三点共线AC=AE探索:我们可以发现,点A 绕中心点О旋转180°后到点A',于是A、O、A'三点在同一条直线上,并且OA=OA'.另外分别在同一条直线上的三点还有B、O、B'和C、O、C';并且OB=OB',OC=OC'提炼概念典例精讲 例:解(1)连结AO并延长AO到点D,使OD=OA,于是得到点A关于点О的对称点D;(2)同样画出点B和点C关于点О的对称点E和F;(3)顺次连结DE、EF、FD.如图10.4.5,△DEF即为所求的三角形.试一试:巩固训练B.B.3.64. 解:(1)①②③是轴对称图形;(2)①③⑤⑥是中心对称图形;(3)①③既是中心对称图形,又是轴对称图形;(4)④既不是中心对称图形,又不是轴对称图形5.解:∵△ABO与△CDO关于点O成中心对称,∴BO=DO,AO=CO.∵AF=CE,∴AO-AF=CO-CE,∴FO=EO,又∵∠DOF=∠EOB,∴△FOD与△EOB关于点O成中心对称,∴DF=BE.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
10.4 中心对称 导学案
课题 10.4 中心对称 单元 第10单元 学科 数学 年级 七年级(下)
教材分析 通过观察、探究了解两个图形关于一点成中心对称的概念,知道中心对称图形和中心对称两者之间的关系.
核心素养分析 通过对中心对称性质的认识,提高分析、归纳、猜想、证明等能力,体会化归、数形结合等数学思想;提高合情推理能力,培养数学说理的习惯与能力,感受数学图形的对称美.
学习目标 1、知道中心对称与中心对称图形的意义.2、知道成中心对称的两个图形的性质,会判断两个图形是否成中心对称,会画一个图形关于一个点成中心对称的图形.
重点 对中心对称的理解与中心对称性质的掌握.
难点 中心对称与轴对称的区别与联系.
教学过程
课前预学 引入思考探究一:在上一节,我们已经看到有不少图形绕某一中心旋转一定角度后,可以与自身重合.如图所示的三个图形都是这样的旋转对称图形.归纳:一个图形绕着中心旋转 后能与自身重合,把这样的图形叫做中心对称图形,这个中心叫做 .2、把一个图形绕着某一点旋转 ,如果它能够和 重合,那么,我们就说这两个图形成中心对称。3、中心对称和中心对称图形是一个概念吗?4、如何确定成中心对称的两个图形的对称中心?想一想 线段、三角形、平行四边形、长方形、正方形、圆分别是中心对称图形吗 如果是,那么对称中心又分别在哪里 线段、平行四边形、长方形、正方形、圆是______________________________________
新知讲解 探究二:如图10.4.2所示,△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,点B的对称点为点________,点C的对称点为点________,点A的对称点为点________.点B绕着点A旋转180°到达点D处,因此,B、A、D三点在同一条直线上,并且AB=AD.A、E三点的位置关系怎样 线段AC、AE的大小关系呢 ___________________________________________________________________________探索在图10.4.3中,△A'B'C'与△ABC关于点О成中心对称,你能从图中找到哪些等量关系 提炼概念归纳总结:性质:成中心对称的两个图形,对称点的连线都经过对称中心,且被对称中心平分.判定:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称. 典例精讲 例:如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.试一试如图10.4.6所示的两个图形成中心对称,你能找到它们的对称中心吗 小明找到了如图10.4.7所示的方法,你呢 你知道其中的理由吗 你还能找到其他的方法吗
课堂练习 巩固训练1.对如图的对称性表述,正确的是( )轴对称图形
B. 中心对称图形
C. 既是轴对称图形又是中心对称图形
D. 既不是轴对称图形又不是中心对称图形
2.下列说法中,错误的是( )A.成中心对称的两个图形面积相等B.成中心对称的两个图形中,对称点的连线被对称轴平分C.中心对称图形的对称中心是对称点连线的中心D.中心对称图形绕对称中心旋转180°后,都能与自身重合3.如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为________.4.观察图形,并回答下面的问题:(1)哪些是轴对称图形?(2)哪些是中心对称图形?(3)哪些既是中心对称图形,又是轴对称图形?(4)哪些既不是中心对称图形,又不是轴对称图形?5.如图,在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 求对称中心E点的坐标.6.如图,△ABO与△CDO关于点O成中心对称,点E,F在线段AC上,且AF=CE,试说明FD=BE.答案引入思考探究一:把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称,想一想:线段的对称中心是线段的中点平行四边形、长方形、正方形的对称中心是它们对角线的交点,圆的对称中心是圆心。探究二:我们可以发现,点A 绕中心点О旋转180°后到点A',于是A、O、A'三点在同一条直线上,并且OA=OA'.另外分别在同一条直线上的三点还有B、O、B'和C、O、C';并且OB=OB',OC=OC'点B的对称点为点D ,点C的对称点为点 E,点A的对称点为点 A.点B绕着点A旋转180°到达点D处,因此,B、A、D三点在同一条直线上,并且AB=AD.C、A、E三点的位置关系怎样 线段AC、AE的大小关系呢 C、A、E三点共线AC=AE探索:我们可以发现,点A 绕中心点О旋转180°后到点A',于是A、O、A'三点在同一条直线上,并且OA=OA'.另外分别在同一条直线上的三点还有B、O、B'和C、O、C';并且OB=OB',OC=OC'提炼概念典例精讲 例:解(1)连结AO并延长AO到点D,使OD=OA,于是得到点A关于点О的对称点D;(2)同样画出点B和点C关于点О的对称点E和F;(3)顺次连结DE、EF、FD.如图10.4.5,△DEF即为所求的三角形.试一试:巩固训练B.B.3.64. 解:(1)①②③是轴对称图形;(2)①③⑤⑥是中心对称图形;(3)①③既是中心对称图形,又是轴对称图形;(4)④既不是中心对称图形,又不是轴对称图形5.解:∵△ABO与△CDO关于点O成中心对称,∴BO=DO,AO=CO.∵AF=CE,∴AO-AF=CO-CE,∴FO=EO,又∵∠DOF=∠EOB,∴△FOD与△EOB关于点O成中心对称,∴DF=BE.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
