北师大版必修1示范教案3.6指数函数、幂函数、对数函数增长的比较
文档属性
| 名称 | 北师大版必修1示范教案3.6指数函数、幂函数、对数函数增长的比较 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-11 16:24:25 | ||
图片预览


文档简介
§6 指数函数、幂函数、对数函数增长的比较
教学分析
函数是描述客观世界变化规律的基本数学模型 ( http: / / www.21cnjy.com ),不同的变化规律需要用不同的函数模型来描述.本节的教学目标是认识指数函数、对数函数、幂函数等函数模型的增长差异,体会直线上升、指数爆炸与对数增长的不同,应用函数模型解决简单问题.课本对几种不同增长的函数模型的认识及应用,都是通过实例来实现的,通过教学让学生认识到数学来自现实生活,数学在现实生活中是有用的.
三维目标
1.借助信息技术,利用函数图像及数据表格,比较指数函数、对数函数以及幂函数的增长差异.
2.恰当运用函数的三种表示方法(解析式、表格、图像),并借助信息技术解决一些实际问题.
3.让学生体会数学在实际问题中的应用价值,培养学生学习兴趣.
重点难点
教学重点:认识指数函数、对数函数、幂函数等函数模型的增长差异,体会直线上升、指数爆炸与对数增长的不同.
教学难点:应用函数模型解决简单问题.
课时安排
1课时
导入新课
思路1.(情境导入)
国际象棋起源于古代印度.相传国王要奖赏国际 ( http: / / www.21cnjy.com )象棋的发明者,问他要什么.发明者说:“请在棋盘的第一个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,依次类推,每个格子里的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”国王觉得这个要求不高,就欣然同意了.假定千粒麦子的质量为40 g,据查,目前世界年度小麦产量为6亿吨,但不能满足发明者要求,这就是指数增长.本节我们讨论指数函数、对数函数、幂函数的增长差异.
思路2.(直接导入)
我们知道,对数函数y=logax(a>1) ( http: / / www.21cnjy.com ),指数函数y=ax(a>1)与幂函数y=xn(n>0)在区间(0,+∞)上都是增函数.但这三类函数的增长是有差异的.本节我们讨论指数函数、对数函数、幂函数的增长差异.
推进新课
①在区间 0,+∞ 上判断y=log2x,y=2x,y=x2的单调性.
②列表并在同一坐标系中画出三个函数的图像.
③结合函数的图像找出其交点坐标.
④请在图像上分别标出使不等式log2x<2x<x2和log2x<x2<2x成立的自变量x的取值范围.
⑤由以上问题你能得出怎样结论?
讨论结果:
①在区间(0,+∞)上函数y=log2x,y=2x,y=x2均为单调增函数.
②见下表与图1.
x 0.2 0.6 1.0 1.4 1.8 2.2 2.6 3.0 3.4 …
y=2x 1.149 1.516 2 2.639 3.482 4.959 6. 063 8 10.556 …
y=x2 0.04 0.36 1 1.96 3.24 4.84 6.67 9 11.56 …
y=log2x -2.322 -0.737 0 0.485 0.848 1.138 1.379 1.585 1.766 …
( http: / / www.21cnjy.com )
图1
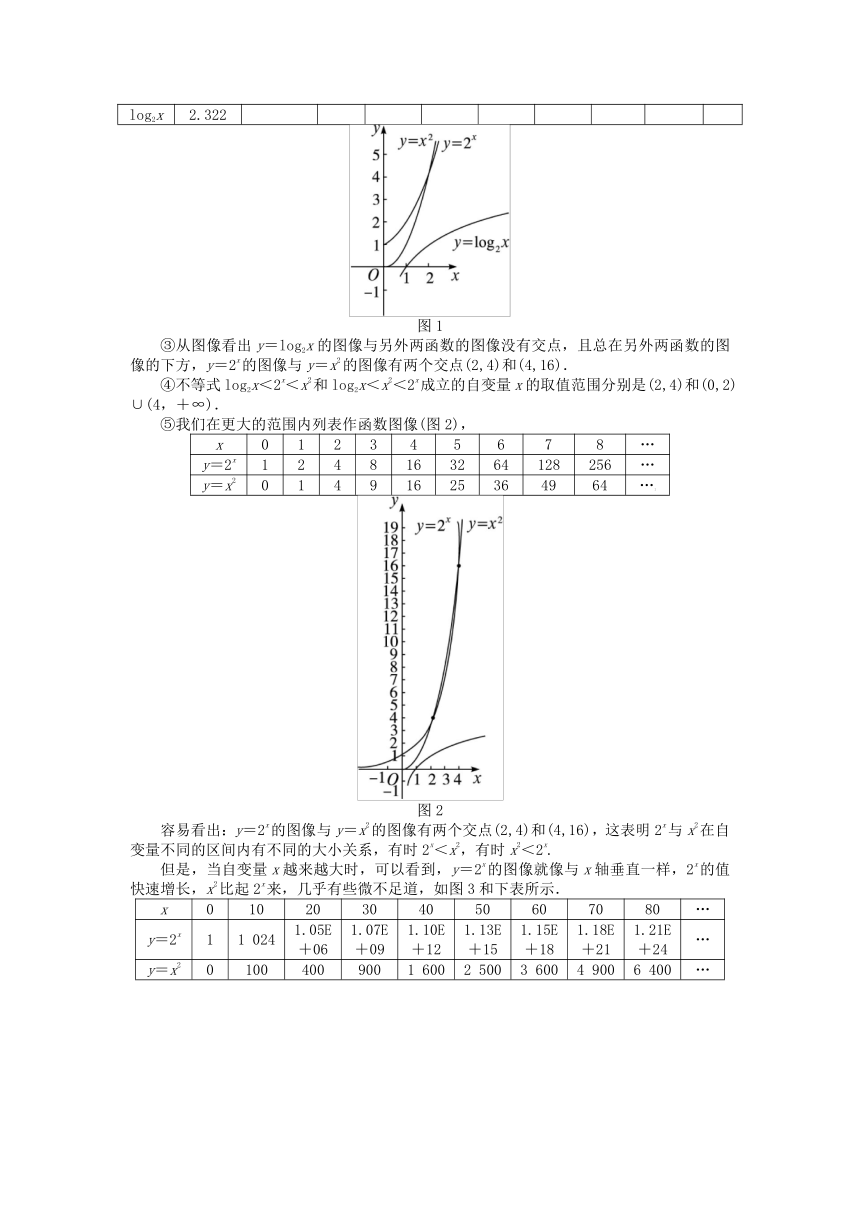
③从图像看出y=log2x ( http: / / www.21cnjy.com )的图像与另外两函数的图像没有交点,且总在另外两函数的图像的下方,y=2x的图像与y=x2的图像有两个交点(2,4)和(4,16).
④不等式log2x<2x<x2和log2x<x2<2x成立的自变量x的取值范围分别是(2,4)和(0,2)∪(4,+∞).
⑤我们在更大的范围内列表作函数图像(图2),
x 0 1 2 3 4 5 6 7 8 …
y=2x 1 2 4 8 16 32 64 128 256 …
y=x2 0 1 4 9 16 25 36 49 64 …]
( http: / / www.21cnjy.com )
图2
容易看出:y=2x的图像与y=x2的图 ( http: / / www.21cnjy.com )像有两个交点(2,4)和(4,16),这表明2x与x2在自变量不同的区间内有不同的大小关系,有时2x<x2,有时x2<2x.
但是,当自变量x越来越大时,可以看 ( http: / / www.21cnjy.com )到,y=2x的图像就像与x轴垂直一样,2x的值快速增长,x2比起2x来,几乎有些微不足道,如图3和下表所示.
x 0 10 20 30 40 50 60 70 80 …
y=2x 1 1 024 1.05E+06 1.07E+09 1.10E+12 1.13E+15 1.15E+18 1.18E+21 1.21E+24 …
y=x2 0 100 400 900 1 600 2 500 3 600 4 900 6 400 …
( http: / / www.21cnjy.com )
图3
一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>0),通过探索可以发现,在区间(0,+∞)上,无论n比a大多少,尽管在x的一定变化范围内,ax会小于xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.
同样地,对于对数函数y=logax ( http: / / www.21cnjy.com )(a>1)和幂函数y=xn(n>0),在区间(0,+∞)上,随着x的增大,logax增长得越来越慢,图像就像是渐渐地与x轴平行一样.尽管在x的一定变化范围内,logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax<xn.
综上所述,尽管对数函数y=logax(a>1 ( http: / / www.21cnjy.com )),指数函数y=ax(a>1)与幂函数y=xn(n>0)在区间(0,+∞)上都是增函数,但它们的增长速度不同,而且不在同一个“档次”上.随着x的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢.因此,总会存在一个x0,当x>x0时,就会有logax<xn<ax.虽然幂函数y=xn(n>0)增长快于对数函数y=logax(a>1)增长,但它们与指数增长比起来相差甚远,因此指数增长又称“指数爆炸”.
思路1
例1 试利用计算器来计算2500的近似值.
活动:学生思考,教师提示, ( http: / / www.21cnjy.com )计算这样一个大的数,用计算器无法直接计算.如何计算呢?我们可以充分利用幂的运算性质,再结合计算器的利用来求其近似值.
解:第一步,利用科学计算器算出
210=1 024=1.024×103;
第二步,再计算2100,因为
2100=(210)10=(1.024×103)10=1.02410×1030,
所以,我们只需要用科学计算器算出
1.02410≈1.267 7,
则2100≈1.267 7×1030;
第三步,再计算2500,因为
(2100)5≈(1.267 7×1030)5,
我们只需要用科学计算器算出
1.267 75≈3.274 0,
从而算出2500≈3.27×10150.
点评:在设计计算方法时,要考虑到科学计算器能计算的位数.如果函数值非常大,我们常常用科学记数法表示,并且根据需要保留一定数目的有效数字.
例2 在自然界中,有些种 ( http: / / www.21cnjy.com )群的世代是隔离,即每一代的生活周期是分离的,例如很多一年生草本植物,在当年结实后死亡,第二年种子萌发产生下一代.假设一个理想种群,其每个个体产生2个后代,又假定种群开始时有10个个体,到第二代时,种群个体将上升为20个,以后每代增加1倍,依次为40,80,160,…,试写出计算过程,归纳种群增长模型,说明何种情况种群上升,种群稳定,种群灭亡.
活动:学生仔细审题,理解题目的含义,教师指导,注意归纳总结.
解:设Nt表示t世代种群的大小,Nt+1表示t+1世代种群的大小,
则N0=10;N1=10×2=20;N2=20×2=40;N3=40×2=80;N4=80×2=160;….
由上述过程归纳成最简单的种群增长模型,由下式表示:Nt+1=R0·Nt,其中R0为世代净繁殖率.
如果种群的R0速率年复一年地增长,则
N1=R0N0,
N2=R0N1=RN0,
N3=R0N2=RN0,
…
Nt=RN0.
R0是种群离散增长模型的重要参数,如果 ( http: / / www.21cnjy.com )R0>1,种群上升;R0=1,种群稳定;0<R0<1,种群下降;R0=0,雌体没有繁殖,种群在一代中死亡.思路2
例3 一工厂生产某种零件,每个零件的成 ( http: / / www.21cnjy.com )本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100时,每多订购1个,订购的全部零件的单价就降低0.02元,但最低出厂单价不低于51元.
(1)一次订购量为多少个时,零件的实际出厂价恰为51元?
(2)设一次订购量为x个时,零件的实际出厂价为p元,写出p=f(x).
(3)当销售商一次订购量分别为500,1 000个时,该工厂的利润分别为多少?
(一个零件的利润=实际出厂价-成本)
解:(1)设一次订购量为a个时,零件的实际出厂价恰好为51元,则a=100+=550个.
(2)p=f(x)=
(3)当销售商一次订购量为x个时, ( http: / / www.21cnjy.com )该工厂的利润为y,则y=(p-40)x=其中x∈N+,故当x=500时,y=6 000;当x=1 000时,y=11 000.
点评:方程中的未知数设出来后可以参与运算,函数解析式为含x,y的等式.
例4 甲、乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
( http: / / www.21cnjy.com )
图4
甲调查表明:每个鱼池平均产量从第1年1万只鳗鱼上升到第6年2万只.
乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.
请你根据提供的信息说明:
(1)第2年全县鱼池的个数及全县出产的鳗鱼总数.
(2)到第6年这个县的鳗鱼养殖业的规模(即总产量)比第1年扩大了还是缩小了?请说明理由.
(3)哪一年的规模(即总产量)最大?请说明理由.
活动:观察函数图像,学生先思考或讨论后再回答,教师点拨、提示:
先观察图像得出相关数据,利用数据找出函数模型.
解:由题意可知,甲图像经过(1,1)和(6,2)两点,
从而求得其解析式为y甲=0.2x+0.8,
乙图像经过(1,30)和(6,10)两点,
从而求得其解析式为y乙=-4x+34.
(1)当x=2时,y甲=0.2×2+0.8=1.2,y乙=-4×2+34=26,y甲·y乙=1.2×26=31.2.
所以第2年鱼池有26个,全县出产的鳗鱼总数为31.2万只.
(2)第1年出产鳗鱼1×30=30(万只),第6年出产鳗鱼2×10=20(万只),可见,第6年这个县的鳗鱼养殖业规划比第1年缩小了.
(3)设当第m年时的规模总产量为n,
那么n=y甲·y乙=(0.2m+0.8)(-4m+34)=-0.8m2+3.6m+27.2
=-0.8(m2-4.5m-34)=-0.8(m-2.25)2+31.25.因此,当m=2时,nmax=31.2,
即第2年时,鳗鱼养殖业的规模最大,最大产量为31.2万只.
某蔬菜基地种植西红柿,由历年市场行情得知 ( http: / / www.21cnjy.com ),从二月一日起的300天内,西红柿市场售价与上市时间的关系用图5(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图5(2)的抛物线段表示.
(1)写出图5(1)表示的市场售价与时间的函数关系式P=f(t);
写出图5(2)表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2)
图5
(注:市场售价和种植成本的单位:元/102 kg,时间单位:天)
活动:学生在黑板上书写解答.教师在学生中巡视其他学生的解答,发现问题及时纠正.
解:(1)由图5(1)可得市场售价与时间的函数关系式为f(t)=
由图5(2)可得种植成本与时间的函数关系式为g(t)=(t-150)2+100,0≤t≤300.
(2)设t时刻的纯收益为h(t),则由题意得h(t)=f(t)-g(t),
即h(t)=
当0≤t≤200时,配方整理,得h(t)=-(t-50)2+100,
所以当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理,得h(t)=-(t-350)2+100,
所以当t=300时,h(t)取得区间[200,300]上的最大值87.5.
综上,由100>87.5可知,h(t ( http: / / www.21cnjy.com ))在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大.
点评:本题主要考查由函数图像建立函数关系式和求函数最大值的问题,考查运用所学知识解决实际问题的能力.
探究内容
①在函数应用中如何利用图像求解析式.
②分段函数解析式的求法.
③函数应用中的最大值、最小值问题.
举例探究:(2007山东省青岛高三教学 ( http: / / www.21cnjy.com )质量检测,理21)某跨国公司是专门生产健身产品的企业,第一批产品A上市销售40天内全部售完,该公司对第一批产品A上市后的国内外市场销售情况进行调研,结果如图6(1)、(2)、(3)所示.其中图6(1)的折线表示的是国外市场的日销售量与上市时间的关系;图6(2)的抛物线表示的是国内市场的日销售量与上市时间的关系;图6(3)的折线表示的是每件产品A的销售利润与上市时间的关系.
( http: / / www.21cnjy.com )
图6
(1)分别写出国外市场的日销售量f(t)、国内市场的日销售量g(t)与第一批产品A上市时间t的关系式;
(2)第一批产品A上市后的哪几天,这家公司的国内和国外日销售利润之和超过6 300万元?
分析:1.利用图像求解析式,先要分清函数类型再利用待定系数法求解析式.
2.在t∈[0,40]上,有几个分界点,请同学们思考应分为几段.
3.回忆函数最值的求法.
解:(1)f(t)=g(t)=-t2+6t(0≤t≤40).
(2)每件A产品销售利润h(t)=
该公司的日销售利润F(t)=
当0≤t≤20时,F(t)=3t,先判断其单调性.
设0≤t1<t2≤20,则F(t1)-F(t2)=3t1-3t2
=-(t1+t2)(t1-t2)2.
∴F(t)在[0,20]上为增函数.
∴F(t)max=F(20)=6 000<6 300.
当20<t≤30时,令60>6 300,
则<t<30;
当30<t≤40时,F(t)=60<60=6 300.
故在第24,25,26,27,28,29天日销售利润超过6 300万元.
点评:1.利用图像求解析式,先要分清函数类型再利用待定系数法求解析式,重点是找出关键点.
2.在t∈[0,40]上,有几个分界点,t=20,t=30两点把区间分为三段.
3.二次函数的最值可用配方法,另外利用单调性求最值也是常用方法之一.
本节学习了:①指数函数、对数函数、二次函数的增长差异.②幂函数、指数函数、对数函数的应用.
习题3—6 1,2.
本节设计从精彩的故事开始,让学 ( http: / / www.21cnjy.com )生从故事中体会数学带来的震撼,然后借助计算机感受不同函数模型的巨大差异.接着通过最新题型训练学生利用函数模型解决实际问题的能力;并且重点训练了由图像转化为函数解析式的能力,因为这是高考的一个重点.本节的每个例题都很精彩,可灵活选用.
[备选例题]
某西部山区的某种特产由于运输的原因,长 ( http: / / www.21cnjy.com )期只能在当地销售,当地政府对该项特产的销售投资收益为:每年投入x万元,可获得利润P=-(x-40)2+100万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每年投入x万元,可获利润Q=-(60-x)2+(60-x)万元.问从10年的累积利润看,该规划方案是否可行?
解:在实施规划前,由题设P=-(x-40)2+100(万元),知每年只需投入40万,即可获得最大利润100万元.
则10年的总利润为W1=100×10=1 000(万元).
实施规划后的前5年中,由题设P=-(x-40)2+100,知每年投入30万元时,有最大利润Pmax=(万元).前5年的利润和为×5=(万元).
设在公路通车的后5年中,每年用x万元投资于本地的销售,而用剩下的(60-x)万元用于外地区的销售投资,则其总利润为
W2=×5+×5=-5(x-30)2+4 950.
当x=30时,(W2)max=4 950(万元).
从而10年的总利润为+4 950(万元).
∵+4 950>1 000,∴该规划方案有极大实施价值.
教学分析
函数是描述客观世界变化规律的基本数学模型 ( http: / / www.21cnjy.com ),不同的变化规律需要用不同的函数模型来描述.本节的教学目标是认识指数函数、对数函数、幂函数等函数模型的增长差异,体会直线上升、指数爆炸与对数增长的不同,应用函数模型解决简单问题.课本对几种不同增长的函数模型的认识及应用,都是通过实例来实现的,通过教学让学生认识到数学来自现实生活,数学在现实生活中是有用的.
三维目标
1.借助信息技术,利用函数图像及数据表格,比较指数函数、对数函数以及幂函数的增长差异.
2.恰当运用函数的三种表示方法(解析式、表格、图像),并借助信息技术解决一些实际问题.
3.让学生体会数学在实际问题中的应用价值,培养学生学习兴趣.
重点难点
教学重点:认识指数函数、对数函数、幂函数等函数模型的增长差异,体会直线上升、指数爆炸与对数增长的不同.
教学难点:应用函数模型解决简单问题.
课时安排
1课时
导入新课
思路1.(情境导入)
国际象棋起源于古代印度.相传国王要奖赏国际 ( http: / / www.21cnjy.com )象棋的发明者,问他要什么.发明者说:“请在棋盘的第一个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,依次类推,每个格子里的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”国王觉得这个要求不高,就欣然同意了.假定千粒麦子的质量为40 g,据查,目前世界年度小麦产量为6亿吨,但不能满足发明者要求,这就是指数增长.本节我们讨论指数函数、对数函数、幂函数的增长差异.
思路2.(直接导入)
我们知道,对数函数y=logax(a>1) ( http: / / www.21cnjy.com ),指数函数y=ax(a>1)与幂函数y=xn(n>0)在区间(0,+∞)上都是增函数.但这三类函数的增长是有差异的.本节我们讨论指数函数、对数函数、幂函数的增长差异.
推进新课
①在区间 0,+∞ 上判断y=log2x,y=2x,y=x2的单调性.
②列表并在同一坐标系中画出三个函数的图像.
③结合函数的图像找出其交点坐标.
④请在图像上分别标出使不等式log2x<2x<x2和log2x<x2<2x成立的自变量x的取值范围.
⑤由以上问题你能得出怎样结论?
讨论结果:
①在区间(0,+∞)上函数y=log2x,y=2x,y=x2均为单调增函数.
②见下表与图1.
x 0.2 0.6 1.0 1.4 1.8 2.2 2.6 3.0 3.4 …
y=2x 1.149 1.516 2 2.639 3.482 4.959 6. 063 8 10.556 …
y=x2 0.04 0.36 1 1.96 3.24 4.84 6.67 9 11.56 …
y=log2x -2.322 -0.737 0 0.485 0.848 1.138 1.379 1.585 1.766 …
( http: / / www.21cnjy.com )
图1
③从图像看出y=log2x ( http: / / www.21cnjy.com )的图像与另外两函数的图像没有交点,且总在另外两函数的图像的下方,y=2x的图像与y=x2的图像有两个交点(2,4)和(4,16).
④不等式log2x<2x<x2和log2x<x2<2x成立的自变量x的取值范围分别是(2,4)和(0,2)∪(4,+∞).
⑤我们在更大的范围内列表作函数图像(图2),
x 0 1 2 3 4 5 6 7 8 …
y=2x 1 2 4 8 16 32 64 128 256 …
y=x2 0 1 4 9 16 25 36 49 64 …]
( http: / / www.21cnjy.com )
图2
容易看出:y=2x的图像与y=x2的图 ( http: / / www.21cnjy.com )像有两个交点(2,4)和(4,16),这表明2x与x2在自变量不同的区间内有不同的大小关系,有时2x<x2,有时x2<2x.
但是,当自变量x越来越大时,可以看 ( http: / / www.21cnjy.com )到,y=2x的图像就像与x轴垂直一样,2x的值快速增长,x2比起2x来,几乎有些微不足道,如图3和下表所示.
x 0 10 20 30 40 50 60 70 80 …
y=2x 1 1 024 1.05E+06 1.07E+09 1.10E+12 1.13E+15 1.15E+18 1.18E+21 1.21E+24 …
y=x2 0 100 400 900 1 600 2 500 3 600 4 900 6 400 …
( http: / / www.21cnjy.com )
图3
一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>0),通过探索可以发现,在区间(0,+∞)上,无论n比a大多少,尽管在x的一定变化范围内,ax会小于xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.
同样地,对于对数函数y=logax ( http: / / www.21cnjy.com )(a>1)和幂函数y=xn(n>0),在区间(0,+∞)上,随着x的增大,logax增长得越来越慢,图像就像是渐渐地与x轴平行一样.尽管在x的一定变化范围内,logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax<xn.
综上所述,尽管对数函数y=logax(a>1 ( http: / / www.21cnjy.com )),指数函数y=ax(a>1)与幂函数y=xn(n>0)在区间(0,+∞)上都是增函数,但它们的增长速度不同,而且不在同一个“档次”上.随着x的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢.因此,总会存在一个x0,当x>x0时,就会有logax<xn<ax.虽然幂函数y=xn(n>0)增长快于对数函数y=logax(a>1)增长,但它们与指数增长比起来相差甚远,因此指数增长又称“指数爆炸”.
思路1
例1 试利用计算器来计算2500的近似值.
活动:学生思考,教师提示, ( http: / / www.21cnjy.com )计算这样一个大的数,用计算器无法直接计算.如何计算呢?我们可以充分利用幂的运算性质,再结合计算器的利用来求其近似值.
解:第一步,利用科学计算器算出
210=1 024=1.024×103;
第二步,再计算2100,因为
2100=(210)10=(1.024×103)10=1.02410×1030,
所以,我们只需要用科学计算器算出
1.02410≈1.267 7,
则2100≈1.267 7×1030;
第三步,再计算2500,因为
(2100)5≈(1.267 7×1030)5,
我们只需要用科学计算器算出
1.267 75≈3.274 0,
从而算出2500≈3.27×10150.
点评:在设计计算方法时,要考虑到科学计算器能计算的位数.如果函数值非常大,我们常常用科学记数法表示,并且根据需要保留一定数目的有效数字.
例2 在自然界中,有些种 ( http: / / www.21cnjy.com )群的世代是隔离,即每一代的生活周期是分离的,例如很多一年生草本植物,在当年结实后死亡,第二年种子萌发产生下一代.假设一个理想种群,其每个个体产生2个后代,又假定种群开始时有10个个体,到第二代时,种群个体将上升为20个,以后每代增加1倍,依次为40,80,160,…,试写出计算过程,归纳种群增长模型,说明何种情况种群上升,种群稳定,种群灭亡.
活动:学生仔细审题,理解题目的含义,教师指导,注意归纳总结.
解:设Nt表示t世代种群的大小,Nt+1表示t+1世代种群的大小,
则N0=10;N1=10×2=20;N2=20×2=40;N3=40×2=80;N4=80×2=160;….
由上述过程归纳成最简单的种群增长模型,由下式表示:Nt+1=R0·Nt,其中R0为世代净繁殖率.
如果种群的R0速率年复一年地增长,则
N1=R0N0,
N2=R0N1=RN0,
N3=R0N2=RN0,
…
Nt=RN0.
R0是种群离散增长模型的重要参数,如果 ( http: / / www.21cnjy.com )R0>1,种群上升;R0=1,种群稳定;0<R0<1,种群下降;R0=0,雌体没有繁殖,种群在一代中死亡.思路2
例3 一工厂生产某种零件,每个零件的成 ( http: / / www.21cnjy.com )本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100时,每多订购1个,订购的全部零件的单价就降低0.02元,但最低出厂单价不低于51元.
(1)一次订购量为多少个时,零件的实际出厂价恰为51元?
(2)设一次订购量为x个时,零件的实际出厂价为p元,写出p=f(x).
(3)当销售商一次订购量分别为500,1 000个时,该工厂的利润分别为多少?
(一个零件的利润=实际出厂价-成本)
解:(1)设一次订购量为a个时,零件的实际出厂价恰好为51元,则a=100+=550个.
(2)p=f(x)=
(3)当销售商一次订购量为x个时, ( http: / / www.21cnjy.com )该工厂的利润为y,则y=(p-40)x=其中x∈N+,故当x=500时,y=6 000;当x=1 000时,y=11 000.
点评:方程中的未知数设出来后可以参与运算,函数解析式为含x,y的等式.
例4 甲、乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
( http: / / www.21cnjy.com )
图4
甲调查表明:每个鱼池平均产量从第1年1万只鳗鱼上升到第6年2万只.
乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.
请你根据提供的信息说明:
(1)第2年全县鱼池的个数及全县出产的鳗鱼总数.
(2)到第6年这个县的鳗鱼养殖业的规模(即总产量)比第1年扩大了还是缩小了?请说明理由.
(3)哪一年的规模(即总产量)最大?请说明理由.
活动:观察函数图像,学生先思考或讨论后再回答,教师点拨、提示:
先观察图像得出相关数据,利用数据找出函数模型.
解:由题意可知,甲图像经过(1,1)和(6,2)两点,
从而求得其解析式为y甲=0.2x+0.8,
乙图像经过(1,30)和(6,10)两点,
从而求得其解析式为y乙=-4x+34.
(1)当x=2时,y甲=0.2×2+0.8=1.2,y乙=-4×2+34=26,y甲·y乙=1.2×26=31.2.
所以第2年鱼池有26个,全县出产的鳗鱼总数为31.2万只.
(2)第1年出产鳗鱼1×30=30(万只),第6年出产鳗鱼2×10=20(万只),可见,第6年这个县的鳗鱼养殖业规划比第1年缩小了.
(3)设当第m年时的规模总产量为n,
那么n=y甲·y乙=(0.2m+0.8)(-4m+34)=-0.8m2+3.6m+27.2
=-0.8(m2-4.5m-34)=-0.8(m-2.25)2+31.25.因此,当m=2时,nmax=31.2,
即第2年时,鳗鱼养殖业的规模最大,最大产量为31.2万只.
某蔬菜基地种植西红柿,由历年市场行情得知 ( http: / / www.21cnjy.com ),从二月一日起的300天内,西红柿市场售价与上市时间的关系用图5(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图5(2)的抛物线段表示.
(1)写出图5(1)表示的市场售价与时间的函数关系式P=f(t);
写出图5(2)表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2)
图5
(注:市场售价和种植成本的单位:元/102 kg,时间单位:天)
活动:学生在黑板上书写解答.教师在学生中巡视其他学生的解答,发现问题及时纠正.
解:(1)由图5(1)可得市场售价与时间的函数关系式为f(t)=
由图5(2)可得种植成本与时间的函数关系式为g(t)=(t-150)2+100,0≤t≤300.
(2)设t时刻的纯收益为h(t),则由题意得h(t)=f(t)-g(t),
即h(t)=
当0≤t≤200时,配方整理,得h(t)=-(t-50)2+100,
所以当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理,得h(t)=-(t-350)2+100,
所以当t=300时,h(t)取得区间[200,300]上的最大值87.5.
综上,由100>87.5可知,h(t ( http: / / www.21cnjy.com ))在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大.
点评:本题主要考查由函数图像建立函数关系式和求函数最大值的问题,考查运用所学知识解决实际问题的能力.
探究内容
①在函数应用中如何利用图像求解析式.
②分段函数解析式的求法.
③函数应用中的最大值、最小值问题.
举例探究:(2007山东省青岛高三教学 ( http: / / www.21cnjy.com )质量检测,理21)某跨国公司是专门生产健身产品的企业,第一批产品A上市销售40天内全部售完,该公司对第一批产品A上市后的国内外市场销售情况进行调研,结果如图6(1)、(2)、(3)所示.其中图6(1)的折线表示的是国外市场的日销售量与上市时间的关系;图6(2)的抛物线表示的是国内市场的日销售量与上市时间的关系;图6(3)的折线表示的是每件产品A的销售利润与上市时间的关系.
( http: / / www.21cnjy.com )
图6
(1)分别写出国外市场的日销售量f(t)、国内市场的日销售量g(t)与第一批产品A上市时间t的关系式;
(2)第一批产品A上市后的哪几天,这家公司的国内和国外日销售利润之和超过6 300万元?
分析:1.利用图像求解析式,先要分清函数类型再利用待定系数法求解析式.
2.在t∈[0,40]上,有几个分界点,请同学们思考应分为几段.
3.回忆函数最值的求法.
解:(1)f(t)=g(t)=-t2+6t(0≤t≤40).
(2)每件A产品销售利润h(t)=
该公司的日销售利润F(t)=
当0≤t≤20时,F(t)=3t,先判断其单调性.
设0≤t1<t2≤20,则F(t1)-F(t2)=3t1-3t2
=-(t1+t2)(t1-t2)2.
∴F(t)在[0,20]上为增函数.
∴F(t)max=F(20)=6 000<6 300.
当20<t≤30时,令60>6 300,
则<t<30;
当30<t≤40时,F(t)=60<60=6 300.
故在第24,25,26,27,28,29天日销售利润超过6 300万元.
点评:1.利用图像求解析式,先要分清函数类型再利用待定系数法求解析式,重点是找出关键点.
2.在t∈[0,40]上,有几个分界点,t=20,t=30两点把区间分为三段.
3.二次函数的最值可用配方法,另外利用单调性求最值也是常用方法之一.
本节学习了:①指数函数、对数函数、二次函数的增长差异.②幂函数、指数函数、对数函数的应用.
习题3—6 1,2.
本节设计从精彩的故事开始,让学 ( http: / / www.21cnjy.com )生从故事中体会数学带来的震撼,然后借助计算机感受不同函数模型的巨大差异.接着通过最新题型训练学生利用函数模型解决实际问题的能力;并且重点训练了由图像转化为函数解析式的能力,因为这是高考的一个重点.本节的每个例题都很精彩,可灵活选用.
[备选例题]
某西部山区的某种特产由于运输的原因,长 ( http: / / www.21cnjy.com )期只能在当地销售,当地政府对该项特产的销售投资收益为:每年投入x万元,可获得利润P=-(x-40)2+100万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划后对该项目每年都投入60万元的销售投资,在未来10年的前5年中,每年都从60万元中拨出30万元用于修建一条公路,5年修成,通车前该特产只能在当地销售;公路通车后的5年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每年投入x万元,可获利润Q=-(60-x)2+(60-x)万元.问从10年的累积利润看,该规划方案是否可行?
解:在实施规划前,由题设P=-(x-40)2+100(万元),知每年只需投入40万,即可获得最大利润100万元.
则10年的总利润为W1=100×10=1 000(万元).
实施规划后的前5年中,由题设P=-(x-40)2+100,知每年投入30万元时,有最大利润Pmax=(万元).前5年的利润和为×5=(万元).
设在公路通车的后5年中,每年用x万元投资于本地的销售,而用剩下的(60-x)万元用于外地区的销售投资,则其总利润为
W2=×5+×5=-5(x-30)2+4 950.
当x=30时,(W2)max=4 950(万元).
从而10年的总利润为+4 950(万元).
∵+4 950>1 000,∴该规划方案有极大实施价值.
