8.2.1两角和与差的余弦 学案(无答案)
文档属性
| 名称 | 8.2.1两角和与差的余弦 学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 435.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-27 21:38:26 | ||
图片预览


文档简介
(
审核
编制
) (
两角和与差的余弦
课题
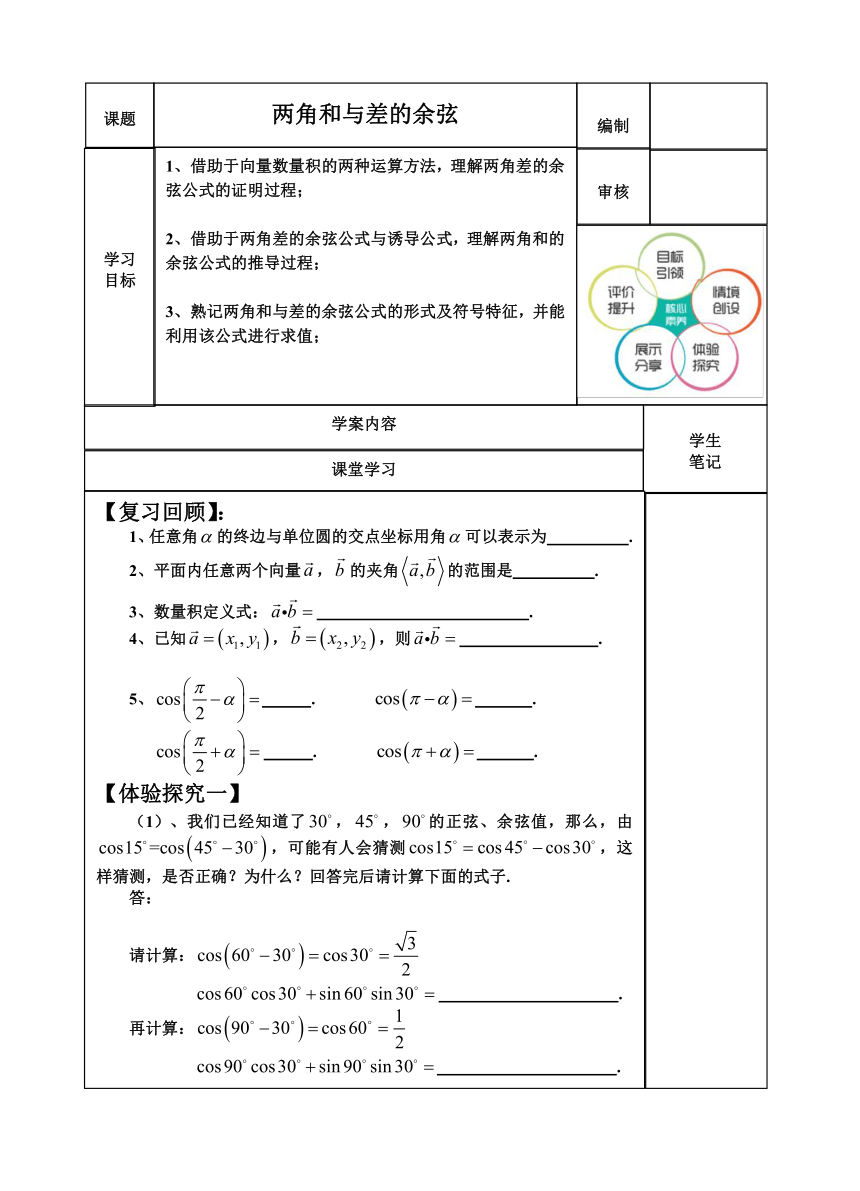
借助于向量数量积的两种运算方法,理解两角差的余弦公式的证明过程;
借助于两角差的余弦公式与诱导公式,理解两角和的余弦公式的推导过程;
熟记两角和与差的余弦公式的形式及符号特征,并能利用该公式进行求值;
学习目标
)
(
课堂学习
学生
笔记
学案内容
【复习回顾】:
1
、任意角
的终边与单位圆的交点坐标用角
可以表示为
.
2
、平面内任意两个向量
,
的夹角
的范围是
.
3
、数量积定义式:
.
4
、已知
,
,则
.
5
、
.
.
.
.
【体验探究一】
、我们已经知道了
,
,
的正弦、余弦值,那么,由
,可能有人会猜测
,这样猜测,是否正确?为什么?回答完后请计算下面的式子
.
答:
请计算:
.
再计算:
.
)
(
学生笔记
) (
学案内容
)
(
图
3
图
4
) (
、根据(
1
)的分析,可知
与
不一定相等,根据上面的计算,你能猜测出
的表达式吗?
.
【体验探究二】
1
、问题
1
:在平面直角坐标系中,由转角的概念可知,当角的终边按逆时针旋转时,角如何变化?
2
、如图所示,用适当的角“
”与“
”表示
的大小
(
1
)、已知
,
(
2
)、已知
,
则
.
则
.
(
3
)、观察图
3
与图
4
,角
的终边是射线
,角
的终边为射线
,
由图
3
可得
.
由图
4
可得
.
进一步,
.
【体验探究三】
结合图
3
与图
4
,请运用向量数量积的定义和坐标运算,并结合【体验探究二】的学习,证明你在【体验探究一】(
2
)问的猜想,完成后面的填空。
证明:在平面直角坐标系
中,设
,
的终边与单位圆的交点分别为
,
,则点
,
因此,
,
,
)
(
学生笔记
) (
学案内容
) (
从而根据向量的坐标运算公式有:
.
另,由
2--
(
3
)的结论可知:
.
又因为
.
故由数量积的定义式可得:
.
请运用上面的公式,求
的值
思考:怎样求
的值呢?
结合上例的方法,请运用公式
与诱导公式证明
证明
:
【两角和与差的余弦公式】
)
(
记忆方法:
)
(
故
.
)
(
:
.
)
(
:
.
)
(
Eg1
利用
与
证明以下公式
.
(
1
)、
(
2
)
Eg2
、求
的值
【变式训练】:求
的值
)
(
课堂小结
) (
这节课你学到了什么?
)
(
【
巩固提高
】
1
、
的值为
. 3
、化简
的值为
. 4
、化简
)
审核
编制
) (
两角和与差的余弦
课题
借助于向量数量积的两种运算方法,理解两角差的余弦公式的证明过程;
借助于两角差的余弦公式与诱导公式,理解两角和的余弦公式的推导过程;
熟记两角和与差的余弦公式的形式及符号特征,并能利用该公式进行求值;
学习目标
)
(
课堂学习
学生
笔记
学案内容
【复习回顾】:
1
、任意角
的终边与单位圆的交点坐标用角
可以表示为
.
2
、平面内任意两个向量
,
的夹角
的范围是
.
3
、数量积定义式:
.
4
、已知
,
,则
.
5
、
.
.
.
.
【体验探究一】
、我们已经知道了
,
,
的正弦、余弦值,那么,由
,可能有人会猜测
,这样猜测,是否正确?为什么?回答完后请计算下面的式子
.
答:
请计算:
.
再计算:
.
)
(
学生笔记
) (
学案内容
)
(
图
3
图
4
) (
、根据(
1
)的分析,可知
与
不一定相等,根据上面的计算,你能猜测出
的表达式吗?
.
【体验探究二】
1
、问题
1
:在平面直角坐标系中,由转角的概念可知,当角的终边按逆时针旋转时,角如何变化?
2
、如图所示,用适当的角“
”与“
”表示
的大小
(
1
)、已知
,
(
2
)、已知
,
则
.
则
.
(
3
)、观察图
3
与图
4
,角
的终边是射线
,角
的终边为射线
,
由图
3
可得
.
由图
4
可得
.
进一步,
.
【体验探究三】
结合图
3
与图
4
,请运用向量数量积的定义和坐标运算,并结合【体验探究二】的学习,证明你在【体验探究一】(
2
)问的猜想,完成后面的填空。
证明:在平面直角坐标系
中,设
,
的终边与单位圆的交点分别为
,
,则点
,
因此,
,
,
)
(
学生笔记
) (
学案内容
) (
从而根据向量的坐标运算公式有:
.
另,由
2--
(
3
)的结论可知:
.
又因为
.
故由数量积的定义式可得:
.
请运用上面的公式,求
的值
思考:怎样求
的值呢?
结合上例的方法,请运用公式
与诱导公式证明
证明
:
【两角和与差的余弦公式】
)
(
记忆方法:
)
(
故
.
)
(
:
.
)
(
:
.
)
(
Eg1
利用
与
证明以下公式
.
(
1
)、
(
2
)
Eg2
、求
的值
【变式训练】:求
的值
)
(
课堂小结
) (
这节课你学到了什么?
)
(
【
巩固提高
】
1
、
的值为
. 3
、化简
的值为
. 4
、化简
)
