山东省德州市禹城市2022-2023学年八年级上学期期末数学试题(含答案)
文档属性
| 名称 | 山东省德州市禹城市2022-2023学年八年级上学期期末数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 747.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 08:17:01 | ||
图片预览



文档简介
2022~2023学年第一学期期末教学质量检测
八年级数学试题
(满分150分 时间120分钟)
一、选择题(每题4分,共48分)
1.某班开展了以喜迎学校冬季运动会为主题的海报评比活动.下列属于轴对称图形的是( )
A. B. C. D.
2.下列代数式中是分式的为( )
A. B. C. D.
3.如图,BC=BE,CD=ED,则△BCD≌△BED,其依据是( )
A.SAS B.AAS C.SSS D.ASA
4.计算结果是( )
A. B. C. D.
5.小李家和小王家到学校的直线距离分别是5km和7km,那么他们两家的直线距离不可能是( )
A.1km B.2km C.3km D.10km
6.若,那么代数式M应是( )
A. B. C. D.
7.如图,已知∠1+∠2+∠3+∠4=280°,那么∠5的度数为( )
A.80° B.90° C.100° D.110°
8.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,则剩下的钢板的面积为( )
A. B. C. D.
9.已知关于x的方程的增根是x=1,则字母a的值为( )
A.1 B.-1 C.2 D.-2
10.如图,小米同学用两把相同的直尺画一个角的平分线:他先将一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小米说:“射线OP就是∠AOB的平分线.”他这样做的依据是( )
A.先由“ASA”得到全等,再由全等三角形的对应角相等得出
B.先由“SAS”得到全等,再由全等三角形的对应角相等得出
C.先由“SSS”得到全等,再由全等三角形的对应角相等得出
D.角的内部到角的两边的距离相等的点在角的平分线上
11.如图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.
15.3分式方程 例:有甲、乙两个工程队,甲队修路400米与乙队修路600米所用时间相等,乙队每天比甲队多修20米,求甲队每天修路的长度. 冰冰: 庆庆:
方程中的x和y表示的意义,下列说法错误的是( )
A.x表示甲队每天修路的长度 B.x表示乙队每天修路的长度
C.y表示甲队修400米所用的时间 D.y表示乙队修600米所用的时间
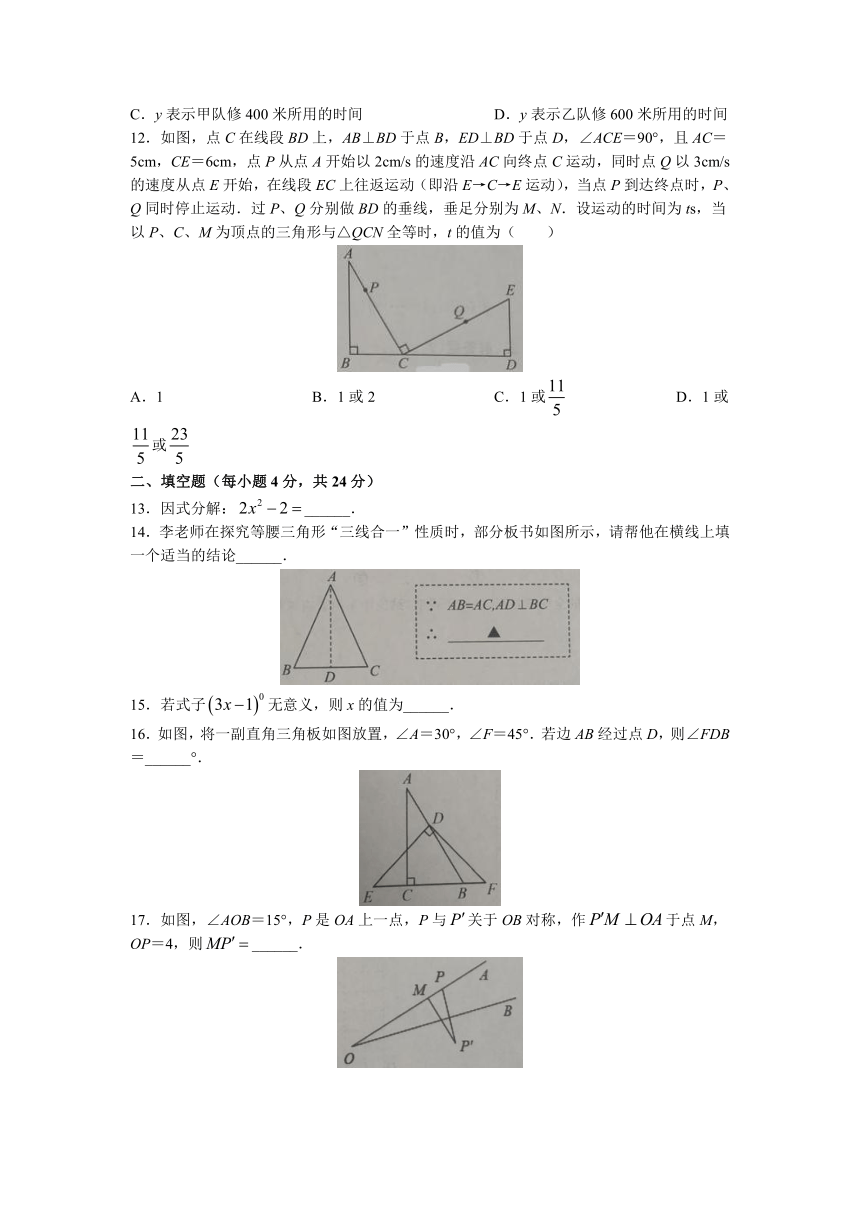
12.如图,点C在线段BD上,AB⊥BD于点B,ED⊥BD于点D,∠ACE=90°,且AC=5cm,CE=6cm,点P从点A开始以2cm/s的速度沿AC向终点C运动,同时点Q以3cm/s的速度从点E开始,在线段EC上往返运动(即沿E→C→E运动),当点P到达终点时,P、Q同时停止运动.过P、Q分别做BD的垂线,垂足分别为M、N.设运动的时间为ts,当以P、C、M为顶点的三角形与△QCN全等时,t的值为( )
A.1 B.1或2 C.1或 D.1或或
二、填空题(每小题4分,共24分)
13.因式分解:______.
14.李老师在探究等腰三角形“三线合一”性质时,部分板书如图所示,请帮他在横线上填一个适当的结论______.
15.若式子无意义,则x的值为______.
16.如图,将一副直角三角板如图放置,∠A=30°,∠F=45°.若边AB经过点D,则∠FDB=______°.
17.如图,∠AOB=15°,P是OA上一点,P与关于OB对称,作于点M,OP=4,则______.
18.对于正数x,规定,例如:,,则______.
三、解答题(共78分)
19.(本题8分)先化简,再求值:,其中x=-1.
20.(本题10分)两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
(1)请找出图②中的全等三角形,并给予说明(结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
21.(本题10分)如图,网格中△ABC和△DEF是轴对称图形.
(1)利用网格线,作出△ABC和△DEF的对称轴l;
(2)如图每个小正方形的边长为1,则△ABC的面积为______;
(3)结合所画图形,在直线l上找点P,使PA+PC的值最小,在图中标出点P的位置.
22.(本题12分)小华和小芳约定周末到体育公园打羽毛球,他们两家到体育公园的距离分别是1200米,3000米,小芳骑自行车的平均速度是小华步行平均速度的3倍,若二人同时到达,则小华需提前4分钟出发,求:小华步行的速度和小芳骑自行车的速度.
23.(本题12分)【课本再现】
(1)在十一章《三角形》中,我们学习了三角形的内角和外角,知道了三角形的内角和为180°.如图1,因为∠B+∠A+∠BCA=180°,又因为∠ACD+∠BCA=180°,所以∠B+∠A=∠ACD,这是我们探究的三角形内角和定理的推论,即三角形的外角等于与它不相邻的两个内角的和,同学们,你还有别的方法证明该推论吗?利用图1写出证明过程.
【知识应用】
(2)如图2,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
求证:∠BAC=∠B+2∠E.
24.(本题12分)小明在学习有关整式的知识时,发现一个有趣的现象:对于关于x的多项式,由于,所以当x-1取任意一对互为相反数的数时,多项式的值是相等的,例如,当x-1=±1,即x=2或0时,的值均为3;当x-1=±2,即x=3或-1时,的值均为6.
于是小明给出一个定义:对于关于x的多项式,若当x-t取任意一对互为相反数的数量,该多项式的值相等,就称该多项式关于x=t对称.例如关于x=1对称.
请结合小明的思考过程,运用此定义解决下列问题:
(1)多项式关于x=______对称;
(2)若关于x的多项式关于x=4对称,求b的值;
(3)整式关于x=______对称.
25.(本题14分)如图①,大正方形的面积可以表示为,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即,同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等.即,把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”.
(1)用上述“面积法”,通过如图②中图形的面积关系,直接写出一个等式:______;
(2)如图③,Rt△ABC中,∠ACB=90°,CA=3,CB=4,AB=5,CH是斜边AB边上的高,用上述“面积法”求CH的长;
(3)如图④,等腰△ABC中,AB=AC=5,CH=4,点O为底边BC上任意一点,OM⊥AB,ON⊥AC,CH⊥AB,垂足分别为点M、N、H,连接AO,求OM+ON的值.
山东省德州禹城市2022-2023学年
八年级上学期2月期末数学试题答案
一、选择题
1-12 CBCAABABDDBC
二、填空题
13. 14.BD=CD,AD平分∠BAC 15.x=1/3
16.15° 17.2 18.
三、解答题
19.解:原式.
当x=-1时,原式=-1+3=2.
20.(1)△ABE≌△ACD,理由如下:
∵△ABC是等腰直角三角形
∴AB=AC,∠BAC=90°,∠B=∠ACB=45°
∵△ADE是等腰直角三角形,∴AE=AD,∠DAE=90°
∴∠BAC+∠EAC=∠DAE+∠EAC,即∠BAE=∠CAD
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS)
(2)∵△ABE≌△ACD,∴∠ACD=∠B=45°
∵∠ACB=45°,∴∠BCD=∠ACB+∠ACD=90°
∴DC⊥BE
21.(1)如图所示,直线l即为所求;
(2)△ABC的面积为,
故答案为:3;
(3)如图所示,点P即为所求.
22.设小明的速度为x米/分钟,则小刚的速度为3x米/分钟,
根据题意得:
解得:x=50
经检验,x=50是原方程的根,并且符合题意,
故3x=150
答:小明的速度为50米/分钟,小刚的速度为150米/分钟.
23.(1)证明:过点C作,∴∠A=∠ACE,∠B=∠DCE,
∴∠ACD=∠A+∠B.
(2)证明:∵CE是△ABC的外角∠ACD的平分线,
∴∠ECD=∠ACE,
∵∠ECD=∠E+∠B,∠BAC=∠E+∠ACE,
∴∠BAC=∠E+∠ECD=∠E+∠E+∠B=∠B+2∠E
24.(1),则多项式关于x=3对称.
故答案为:3;
(2)∵,
∴关于x的多项式关于x=-b对称,
∴-b=4,∴b=-4;
(3)原式,
∴关于x=-3对称.
故答案为:-3.
25.(1)如图(2),大正方形的面积为一个正方形的面积与三个小长方形面积之和,
即,
同时大长方形的面积也可以为,
所以;
故答案为:;
(2)如图(3),Rt△ABC中,∠C=90°,CA=3,CB=4,AB=5,
∵,
∴;
答:CH的长为;
(3)证明:如图(4),
∵OM⊥AB,ON⊥AC,CH⊥AB,垂足分别为点M,N,H,
∴,
∴,
∵AB=AC,∴CH=OM+ON.
即OM+ON=CH.
八年级数学试题
(满分150分 时间120分钟)
一、选择题(每题4分,共48分)
1.某班开展了以喜迎学校冬季运动会为主题的海报评比活动.下列属于轴对称图形的是( )
A. B. C. D.
2.下列代数式中是分式的为( )
A. B. C. D.
3.如图,BC=BE,CD=ED,则△BCD≌△BED,其依据是( )
A.SAS B.AAS C.SSS D.ASA
4.计算结果是( )
A. B. C. D.
5.小李家和小王家到学校的直线距离分别是5km和7km,那么他们两家的直线距离不可能是( )
A.1km B.2km C.3km D.10km
6.若,那么代数式M应是( )
A. B. C. D.
7.如图,已知∠1+∠2+∠3+∠4=280°,那么∠5的度数为( )
A.80° B.90° C.100° D.110°
8.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,则剩下的钢板的面积为( )
A. B. C. D.
9.已知关于x的方程的增根是x=1,则字母a的值为( )
A.1 B.-1 C.2 D.-2
10.如图,小米同学用两把相同的直尺画一个角的平分线:他先将一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小米说:“射线OP就是∠AOB的平分线.”他这样做的依据是( )
A.先由“ASA”得到全等,再由全等三角形的对应角相等得出
B.先由“SAS”得到全等,再由全等三角形的对应角相等得出
C.先由“SSS”得到全等,再由全等三角形的对应角相等得出
D.角的内部到角的两边的距离相等的点在角的平分线上
11.如图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.
15.3分式方程 例:有甲、乙两个工程队,甲队修路400米与乙队修路600米所用时间相等,乙队每天比甲队多修20米,求甲队每天修路的长度. 冰冰: 庆庆:
方程中的x和y表示的意义,下列说法错误的是( )
A.x表示甲队每天修路的长度 B.x表示乙队每天修路的长度
C.y表示甲队修400米所用的时间 D.y表示乙队修600米所用的时间
12.如图,点C在线段BD上,AB⊥BD于点B,ED⊥BD于点D,∠ACE=90°,且AC=5cm,CE=6cm,点P从点A开始以2cm/s的速度沿AC向终点C运动,同时点Q以3cm/s的速度从点E开始,在线段EC上往返运动(即沿E→C→E运动),当点P到达终点时,P、Q同时停止运动.过P、Q分别做BD的垂线,垂足分别为M、N.设运动的时间为ts,当以P、C、M为顶点的三角形与△QCN全等时,t的值为( )
A.1 B.1或2 C.1或 D.1或或
二、填空题(每小题4分,共24分)
13.因式分解:______.
14.李老师在探究等腰三角形“三线合一”性质时,部分板书如图所示,请帮他在横线上填一个适当的结论______.
15.若式子无意义,则x的值为______.
16.如图,将一副直角三角板如图放置,∠A=30°,∠F=45°.若边AB经过点D,则∠FDB=______°.
17.如图,∠AOB=15°,P是OA上一点,P与关于OB对称,作于点M,OP=4,则______.
18.对于正数x,规定,例如:,,则______.
三、解答题(共78分)
19.(本题8分)先化简,再求值:,其中x=-1.
20.(本题10分)两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
(1)请找出图②中的全等三角形,并给予说明(结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
21.(本题10分)如图,网格中△ABC和△DEF是轴对称图形.
(1)利用网格线,作出△ABC和△DEF的对称轴l;
(2)如图每个小正方形的边长为1,则△ABC的面积为______;
(3)结合所画图形,在直线l上找点P,使PA+PC的值最小,在图中标出点P的位置.
22.(本题12分)小华和小芳约定周末到体育公园打羽毛球,他们两家到体育公园的距离分别是1200米,3000米,小芳骑自行车的平均速度是小华步行平均速度的3倍,若二人同时到达,则小华需提前4分钟出发,求:小华步行的速度和小芳骑自行车的速度.
23.(本题12分)【课本再现】
(1)在十一章《三角形》中,我们学习了三角形的内角和外角,知道了三角形的内角和为180°.如图1,因为∠B+∠A+∠BCA=180°,又因为∠ACD+∠BCA=180°,所以∠B+∠A=∠ACD,这是我们探究的三角形内角和定理的推论,即三角形的外角等于与它不相邻的两个内角的和,同学们,你还有别的方法证明该推论吗?利用图1写出证明过程.
【知识应用】
(2)如图2,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
求证:∠BAC=∠B+2∠E.
24.(本题12分)小明在学习有关整式的知识时,发现一个有趣的现象:对于关于x的多项式,由于,所以当x-1取任意一对互为相反数的数时,多项式的值是相等的,例如,当x-1=±1,即x=2或0时,的值均为3;当x-1=±2,即x=3或-1时,的值均为6.
于是小明给出一个定义:对于关于x的多项式,若当x-t取任意一对互为相反数的数量,该多项式的值相等,就称该多项式关于x=t对称.例如关于x=1对称.
请结合小明的思考过程,运用此定义解决下列问题:
(1)多项式关于x=______对称;
(2)若关于x的多项式关于x=4对称,求b的值;
(3)整式关于x=______对称.
25.(本题14分)如图①,大正方形的面积可以表示为,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即,同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等.即,把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”.
(1)用上述“面积法”,通过如图②中图形的面积关系,直接写出一个等式:______;
(2)如图③,Rt△ABC中,∠ACB=90°,CA=3,CB=4,AB=5,CH是斜边AB边上的高,用上述“面积法”求CH的长;
(3)如图④,等腰△ABC中,AB=AC=5,CH=4,点O为底边BC上任意一点,OM⊥AB,ON⊥AC,CH⊥AB,垂足分别为点M、N、H,连接AO,求OM+ON的值.
山东省德州禹城市2022-2023学年
八年级上学期2月期末数学试题答案
一、选择题
1-12 CBCAABABDDBC
二、填空题
13. 14.BD=CD,AD平分∠BAC 15.x=1/3
16.15° 17.2 18.
三、解答题
19.解:原式.
当x=-1时,原式=-1+3=2.
20.(1)△ABE≌△ACD,理由如下:
∵△ABC是等腰直角三角形
∴AB=AC,∠BAC=90°,∠B=∠ACB=45°
∵△ADE是等腰直角三角形,∴AE=AD,∠DAE=90°
∴∠BAC+∠EAC=∠DAE+∠EAC,即∠BAE=∠CAD
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS)
(2)∵△ABE≌△ACD,∴∠ACD=∠B=45°
∵∠ACB=45°,∴∠BCD=∠ACB+∠ACD=90°
∴DC⊥BE
21.(1)如图所示,直线l即为所求;
(2)△ABC的面积为,
故答案为:3;
(3)如图所示,点P即为所求.
22.设小明的速度为x米/分钟,则小刚的速度为3x米/分钟,
根据题意得:
解得:x=50
经检验,x=50是原方程的根,并且符合题意,
故3x=150
答:小明的速度为50米/分钟,小刚的速度为150米/分钟.
23.(1)证明:过点C作,∴∠A=∠ACE,∠B=∠DCE,
∴∠ACD=∠A+∠B.
(2)证明:∵CE是△ABC的外角∠ACD的平分线,
∴∠ECD=∠ACE,
∵∠ECD=∠E+∠B,∠BAC=∠E+∠ACE,
∴∠BAC=∠E+∠ECD=∠E+∠E+∠B=∠B+2∠E
24.(1),则多项式关于x=3对称.
故答案为:3;
(2)∵,
∴关于x的多项式关于x=-b对称,
∴-b=4,∴b=-4;
(3)原式,
∴关于x=-3对称.
故答案为:-3.
25.(1)如图(2),大正方形的面积为一个正方形的面积与三个小长方形面积之和,
即,
同时大长方形的面积也可以为,
所以;
故答案为:;
(2)如图(3),Rt△ABC中,∠C=90°,CA=3,CB=4,AB=5,
∵,
∴;
答:CH的长为;
(3)证明:如图(4),
∵OM⊥AB,ON⊥AC,CH⊥AB,垂足分别为点M,N,H,
∴,
∴,
∵AB=AC,∴CH=OM+ON.
即OM+ON=CH.
同课章节目录
