5.1.1 对顶角 课件(13张PPT)
文档属性
| 名称 | 5.1.1 对顶角 课件(13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 09:56:14 | ||
图片预览




文档简介
(共13张PPT)
华师大版 七年级 上册
05
相交线与平行线
对顶角
情境导入
相交与平行是平面内两条直线之间的两种基本位置关系. 在我们的周围,平行线与相交线无处不在: 纵横交错的公路,操场上的百米跑道线,伸向远方的两条平直铁轨,……都展示了直线相交或直线平行的形象.
那么,怎样判断直线相交或平行呢?不同的位置关系又有哪些性质呢?这些问题的答案就是本章将要学习的内容.
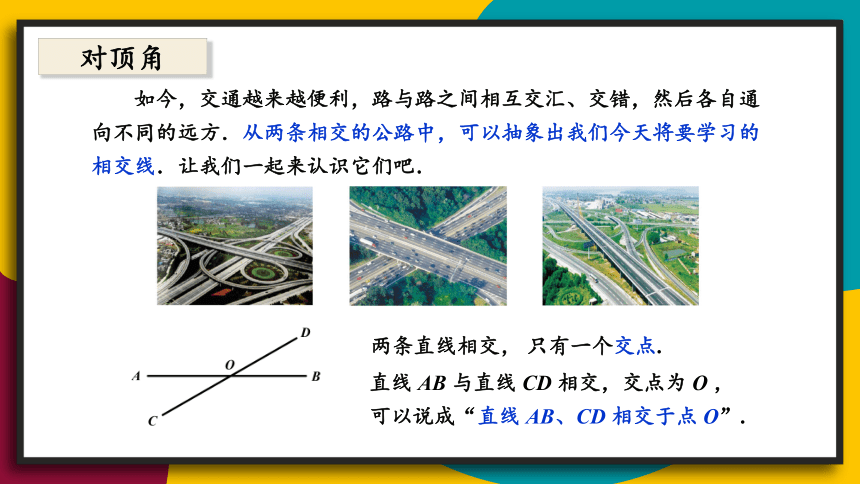
如今,交通越来越便利,路与路之间相互交汇、交错,然后各自通向不同的远方.从两条相交的公路中,可以抽象出我们今天将要学习的相交线.让我们一起来认识它们吧.
对顶角
两条直线相交, 只有一个交点.
直线 AB 与直线 CD 相交,交点为 O ,可以说成“直线 AB、CD 相交于点 O”.
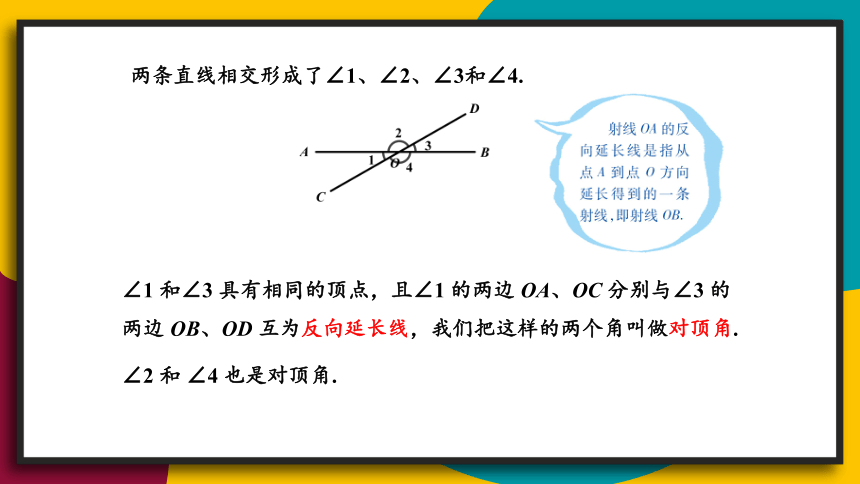
两条直线相交形成了∠1、∠2、∠3和∠4.
从位置关系与数量关系上看,图中哪些角之间存在某种关系呢?
角 ∠1和∠2 ∠2和∠3 ∠3和∠4 ∠4和∠1 ∠1和∠3 ∠2和∠4
位置关系
数量关系
相邻
互补
相邻
互补
相邻
互补
相邻
互补
相对
相等
相对
相等
两条直线相交形成了∠1、∠2、∠3和∠4.
∠1 和∠3 具有相同的顶点,且∠1 的两边 OA、OC 分别与∠3 的两边 OB、OD 互为反向延长线,我们把这样的两个角叫做对顶角.
∠2 和 ∠4 也是对顶角.
如图,∠1=30°,那么∠2、∠3和∠4各等于多少度?图中存在哪些相等关系?
∠2 = 180°-∠1 = 180°-30°= 150°,
∠3 = 180°-∠2 = 180°-150°= 30°,
∠4 = 180°-∠1 = 180°-30°= 150°,
由此,我们得到
∠1 =∠3,∠2 =∠4.
(1)互为对顶角的两个角满足的条件:
①有一个公共顶点;
②一个角的两边分别是另一个角两边的反向延长线.
(2)对顶角是成对出现的,单独的一个角不能称为对顶角.
(3)对顶角反映的是两个角的位置关系,两条相交直线形成 2 对对顶角.
(4)对顶角的性质: 对顶角相等.
如图,直线 AB、CD 相交于点 E,∠AEC = 50°,求∠BED 的度数.
因为直线 AB、CD相交于点E,所以∠AEC与∠BED是对顶角. 根据对顶角相等,得
∠BED = ∠AEC = 50°.
1. 下列各图中的∠1 和∠2 是不是对顶角?
不是
不是
不是
(1)
(2)
(3)
2. 说出各图的对顶角,其中直线 AB、CB 分别与直线 DE 相交于 点 F、G,
直线 IJ、KL分别与直线 MN相交于点 O、P.
∠DFB与∠AFG,
∠DFA 与∠GFB,
∠FGB 与 ∠CGE,
∠FGC与∠BGE.
∠MOJ 与∠IOP,
∠MOI 与∠JOP,
∠OPL 与 ∠KPN,
∠OPK与∠LPN.
(1)
(2)
145
3. 如图,∠1与∠2是对顶角,∠1 = 180°-α,∠2 = 35°,则 α =______°.
课堂小结
对顶角
概念:
性质:
两个角具有相同的顶点,且一个角的两边分别与另一个角的两边互为反向延长线
对顶角相等
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
华师大版 七年级 上册
05
相交线与平行线
对顶角
情境导入
相交与平行是平面内两条直线之间的两种基本位置关系. 在我们的周围,平行线与相交线无处不在: 纵横交错的公路,操场上的百米跑道线,伸向远方的两条平直铁轨,……都展示了直线相交或直线平行的形象.
那么,怎样判断直线相交或平行呢?不同的位置关系又有哪些性质呢?这些问题的答案就是本章将要学习的内容.
如今,交通越来越便利,路与路之间相互交汇、交错,然后各自通向不同的远方.从两条相交的公路中,可以抽象出我们今天将要学习的相交线.让我们一起来认识它们吧.
对顶角
两条直线相交, 只有一个交点.
直线 AB 与直线 CD 相交,交点为 O ,可以说成“直线 AB、CD 相交于点 O”.
两条直线相交形成了∠1、∠2、∠3和∠4.
从位置关系与数量关系上看,图中哪些角之间存在某种关系呢?
角 ∠1和∠2 ∠2和∠3 ∠3和∠4 ∠4和∠1 ∠1和∠3 ∠2和∠4
位置关系
数量关系
相邻
互补
相邻
互补
相邻
互补
相邻
互补
相对
相等
相对
相等
两条直线相交形成了∠1、∠2、∠3和∠4.
∠1 和∠3 具有相同的顶点,且∠1 的两边 OA、OC 分别与∠3 的两边 OB、OD 互为反向延长线,我们把这样的两个角叫做对顶角.
∠2 和 ∠4 也是对顶角.
如图,∠1=30°,那么∠2、∠3和∠4各等于多少度?图中存在哪些相等关系?
∠2 = 180°-∠1 = 180°-30°= 150°,
∠3 = 180°-∠2 = 180°-150°= 30°,
∠4 = 180°-∠1 = 180°-30°= 150°,
由此,我们得到
∠1 =∠3,∠2 =∠4.
(1)互为对顶角的两个角满足的条件:
①有一个公共顶点;
②一个角的两边分别是另一个角两边的反向延长线.
(2)对顶角是成对出现的,单独的一个角不能称为对顶角.
(3)对顶角反映的是两个角的位置关系,两条相交直线形成 2 对对顶角.
(4)对顶角的性质: 对顶角相等.
如图,直线 AB、CD 相交于点 E,∠AEC = 50°,求∠BED 的度数.
因为直线 AB、CD相交于点E,所以∠AEC与∠BED是对顶角. 根据对顶角相等,得
∠BED = ∠AEC = 50°.
1. 下列各图中的∠1 和∠2 是不是对顶角?
不是
不是
不是
(1)
(2)
(3)
2. 说出各图的对顶角,其中直线 AB、CB 分别与直线 DE 相交于 点 F、G,
直线 IJ、KL分别与直线 MN相交于点 O、P.
∠DFB与∠AFG,
∠DFA 与∠GFB,
∠FGB 与 ∠CGE,
∠FGC与∠BGE.
∠MOJ 与∠IOP,
∠MOI 与∠JOP,
∠OPL 与 ∠KPN,
∠OPK与∠LPN.
(1)
(2)
145
3. 如图,∠1与∠2是对顶角,∠1 = 180°-α,∠2 = 35°,则 α =______°.
课堂小结
对顶角
概念:
性质:
两个角具有相同的顶点,且一个角的两边分别与另一个角的两边互为反向延长线
对顶角相等
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
