九年级数学上册试题 3.2用频率估计概率-北师大版(含答案)
文档属性
| 名称 | 九年级数学上册试题 3.2用频率估计概率-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 401.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 08:50:10 | ||
图片预览

文档简介
3.2用频率估计概率
一、选择题
1.口袋里有若干个白球,又放进去6个黑球,这些球除颜色外其他均相同,小明每次摸出一个球并记下颜色后放回,多次摸球后发现摸到白球的频率稳定在,则口袋里的白球数很可能为( )
A.4 B.6 C.9 D.15
2.小明为估计一个不规则图案的面积,采取了以下办法:首先用一个面积为10cm2的长方形将不规则图案围起来(如图①);然后在一固定位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在边界线上或长方形区域外不计试验结果);最后将若干次有效试验的结果绘制成了图②所示的折线统计图.请估计不规则图案的面积大约为( )
A.4cm2 B.3.5 cm2 C.4.5 cm2 D.5 cm2
3.下列判断错误的是( )
A.了解一批冰箱的使用寿命,采用抽样调查的方式
B.一组数据2,5,3,5,6,8的众数和中位数都是5
C.甲、乙两组队员身高数据的方差分别为,,那么甲组队员的身高比较整齐
D.一个不透明的袋子里装有红球、蓝球共20个,这些球除颜色外都相同,小红通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数可能是5个
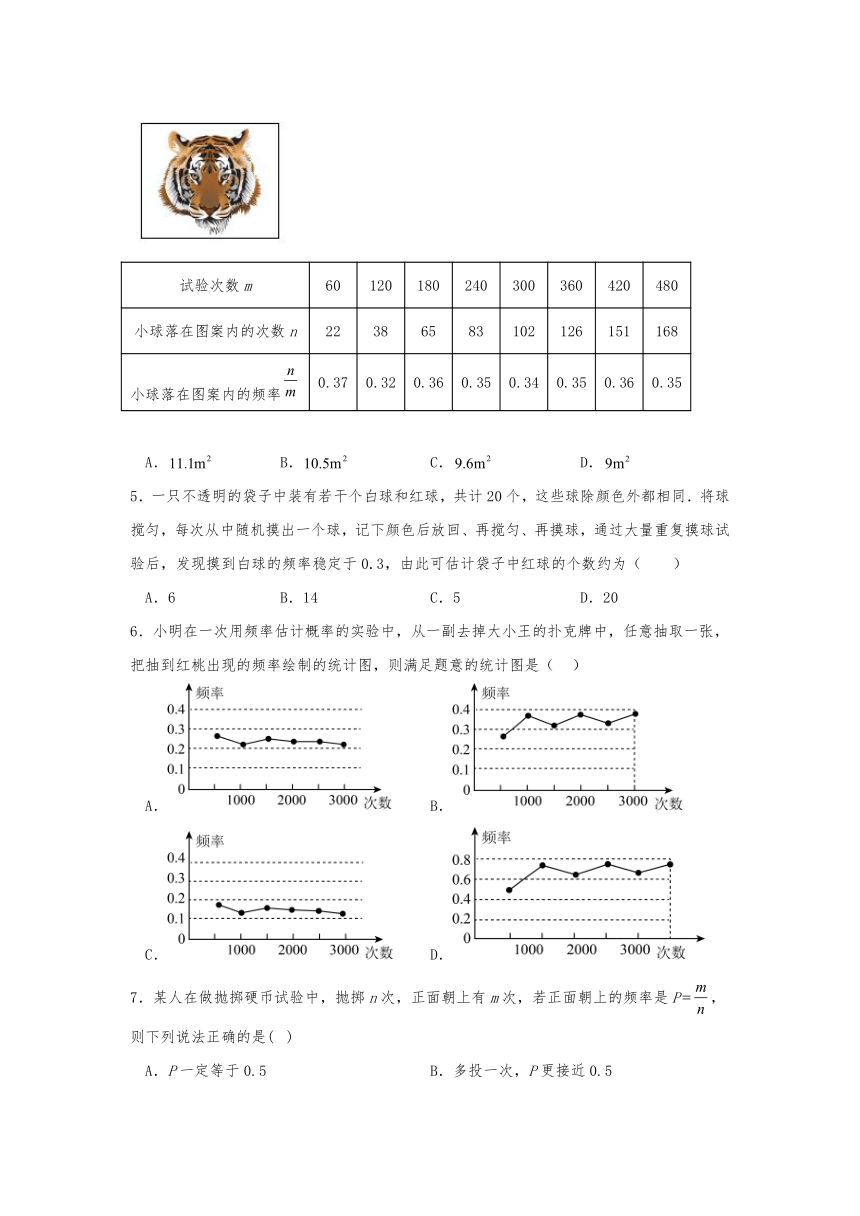
4.如图,小红在一张长为6m,宽为5m的长方形纸上画了一个老虎图案,他想知道该图案的面积大小,于是想了这样一个办法,朝长方形的纸上扔小球,并记录小球落在老虎图案上的次数(球扔在界线上或长方形纸外不计试验结果),他将若干次有效试验的结果整理成统计表,由此他估计此图案的面积大约为( )
试验次数m 60 120 180 240 300 360 420 480
小球落在图案内的次数n 22 38 65 83 102 126 151 168
小球落在图案内的频率 0.37 0.32 0.36 0.35 0.34 0.35 0.36 0.35
A. B. C. D.
5.一只不透明的袋子中装有若干个白球和红球,共计20个,这些球除颜色外都相同.将球搅匀,每次从中随机摸出一个球,记下颜色后放回、再搅匀、再摸球,通过大量重复摸球试验后,发现摸到白球的频率稳定于0.3,由此可估计袋子中红球的个数约为( )
A.6 B.14 C.5 D.20
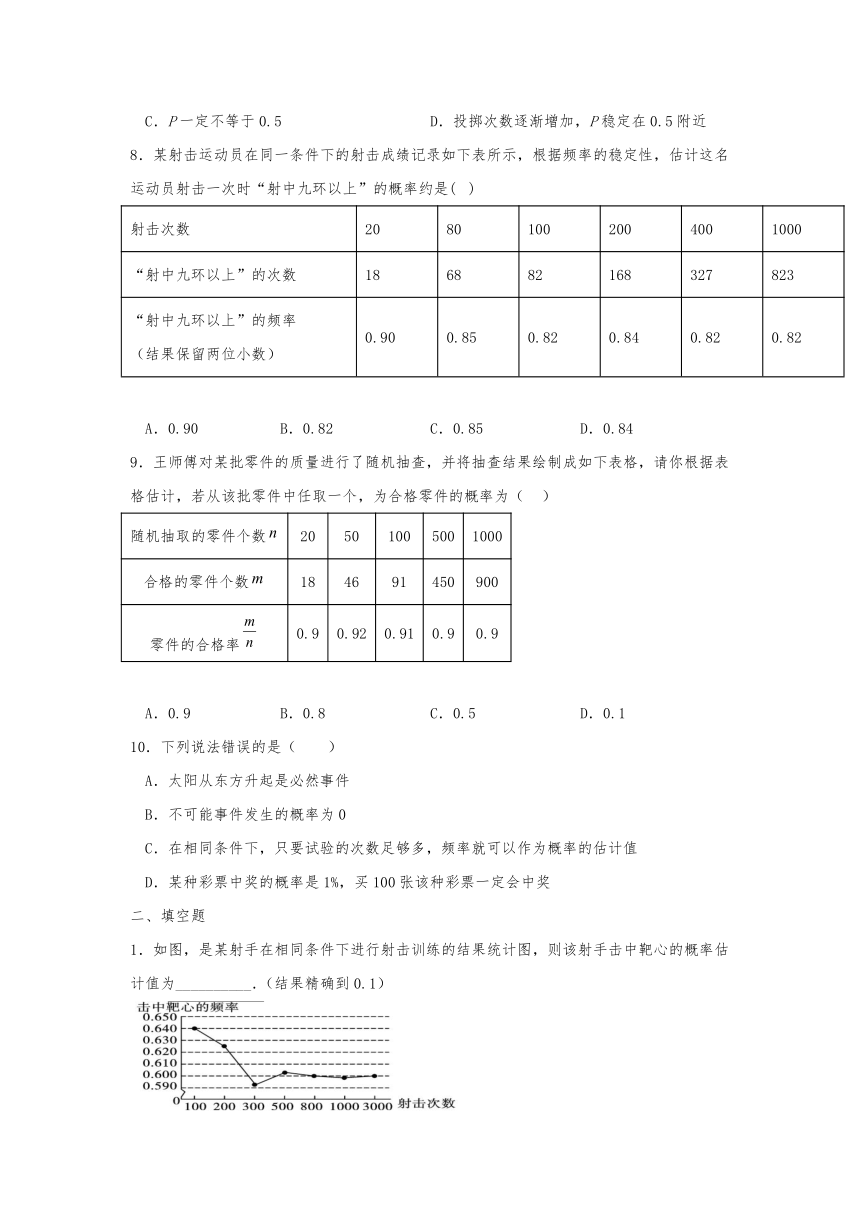
6.小明在一次用频率估计概率的实验中,从一副去掉大小王的扑克牌中,任意抽取一张,把抽到红桃出现的频率绘制的统计图,则满足题意的统计图是( )
A. B.
C. D.
7.某人在做抛掷硬币试验中,抛掷n次,正面朝上有m次,若正面朝上的频率是P,则下列说法正确的是( )
A.P一定等于0.5 B.多投一次,P更接近0.5
C.P一定不等于0.5 D.投掷次数逐渐增加,P稳定在0.5附近
8.某射击运动员在同一条件下的射击成绩记录如下表所示,根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率 (结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
A.0.90 B.0.82 C.0.85 D.0.84
9.王师傅对某批零件的质量进行了随机抽查,并将抽查结果绘制成如下表格,请你根据表格估计,若从该批零件中任取一个,为合格零件的概率为( )
随机抽取的零件个数 20 50 100 500 1000
合格的零件个数 18 46 91 450 900
零件的合格率 0.9 0.92 0.91 0.9 0.9
A.0.9 B.0.8 C.0.5 D.0.1
10.下列说法错误的是( )
A.太阳从东方升起是必然事件
B.不可能事件发生的概率为0
C.在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值
D.某种彩票中奖的概率是1%,买100张该种彩票一定会中奖
二、填空题
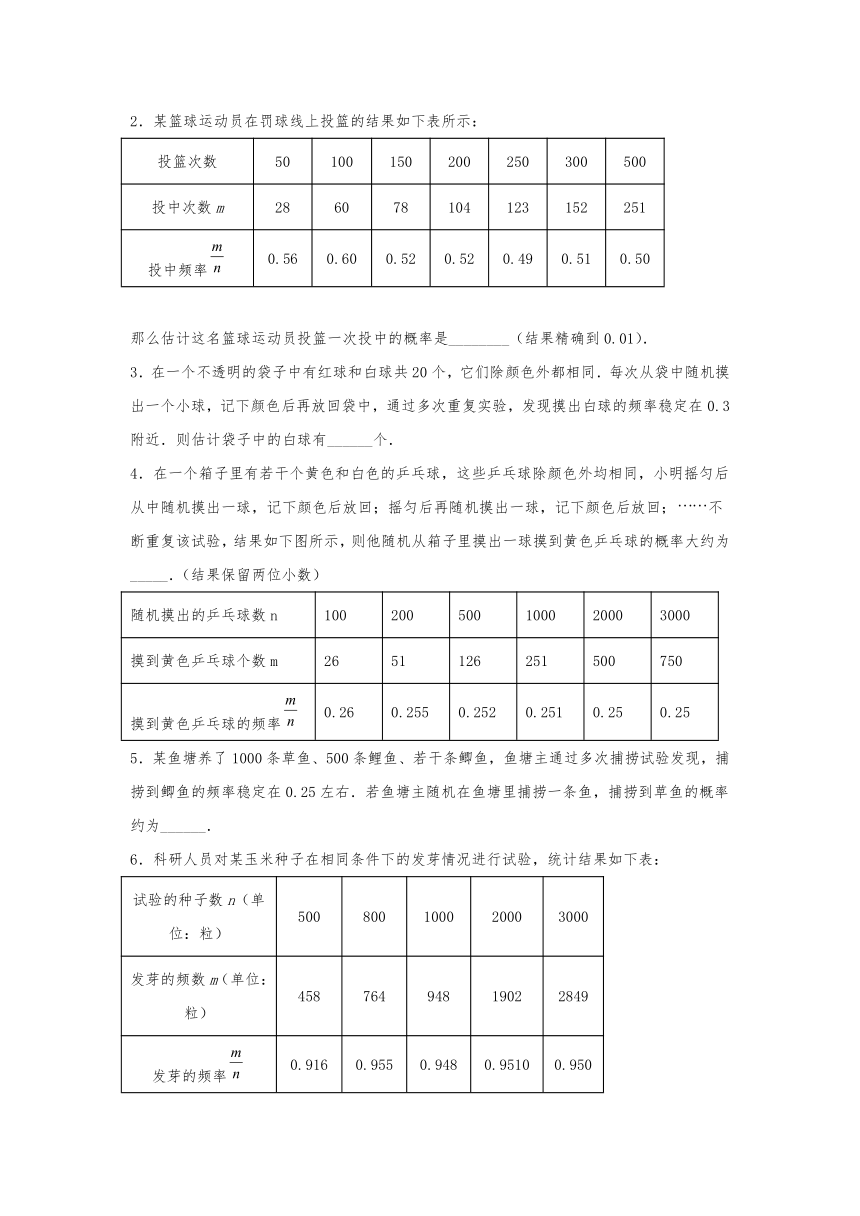
1.如图,是某射手在相同条件下进行射击训练的结果统计图,则该射手击中靶心的概率估计值为__________.(结果精确到0.1)
2.某篮球运动员在罚球线上投篮的结果如下表所示:
投篮次数 50 100 150 200 250 300 500
投中次数m 28 60 78 104 123 152 251
投中频率 0.56 0.60 0.52 0.52 0.49 0.51 0.50
那么估计这名篮球运动员投篮一次投中的概率是________(结果精确到0.01).
3.在一个不透明的袋子中有红球和白球共20个,它们除颜色外都相同.每次从袋中随机摸出一个小球,记下颜色后再放回袋中,通过多次重复实验,发现摸出白球的频率稳定在0.3附近.则估计袋子中的白球有______个.
4.在一个箱子里有若干个黄色和白色的乒乓球,这些乒乓球除颜色外均相同,小明摇匀后从中随机摸出一球,记下颜色后放回;摇匀后再随机摸出一球,记下颜色后放回;不断重复该试验,结果如下图所示,则他随机从箱子里摸出一球摸到黄色乒乓球的概率大约为_____.(结果保留两位小数)
随机摸出的乒乓球数n 100 200 500 1000 2000 3000
摸到黄色乒乓球个数m 26 51 126 251 500 750
摸到黄色乒乓球的频率 0.26 0.255 0.252 0.251 0.25 0.25
5.某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼,鱼塘主通过多次捕捞试验发现,捕捞到鲫鱼的频率稳定在0.25左右.若鱼塘主随机在鱼塘里捕捞一条鱼,捕捞到草鱼的概率约为______.
6.科研人员对某玉米种子在相同条件下的发芽情况进行试验,统计结果如下表:
试验的种子数n(单位:粒) 500 800 1000 2000 3000
发芽的频数m(单位:粒) 458 764 948 1902 2849
发芽的频率 0.916 0.955 0.948 0.9510 0.950
根据统计结果,该玉米种子发芽的概率估计值为______(结果精确到0.01).
7.在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则盒子中大约有白球_______个.
8.在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.3,摸到红球的频率是 _____,则估计盒子中大约有红球 _____个.
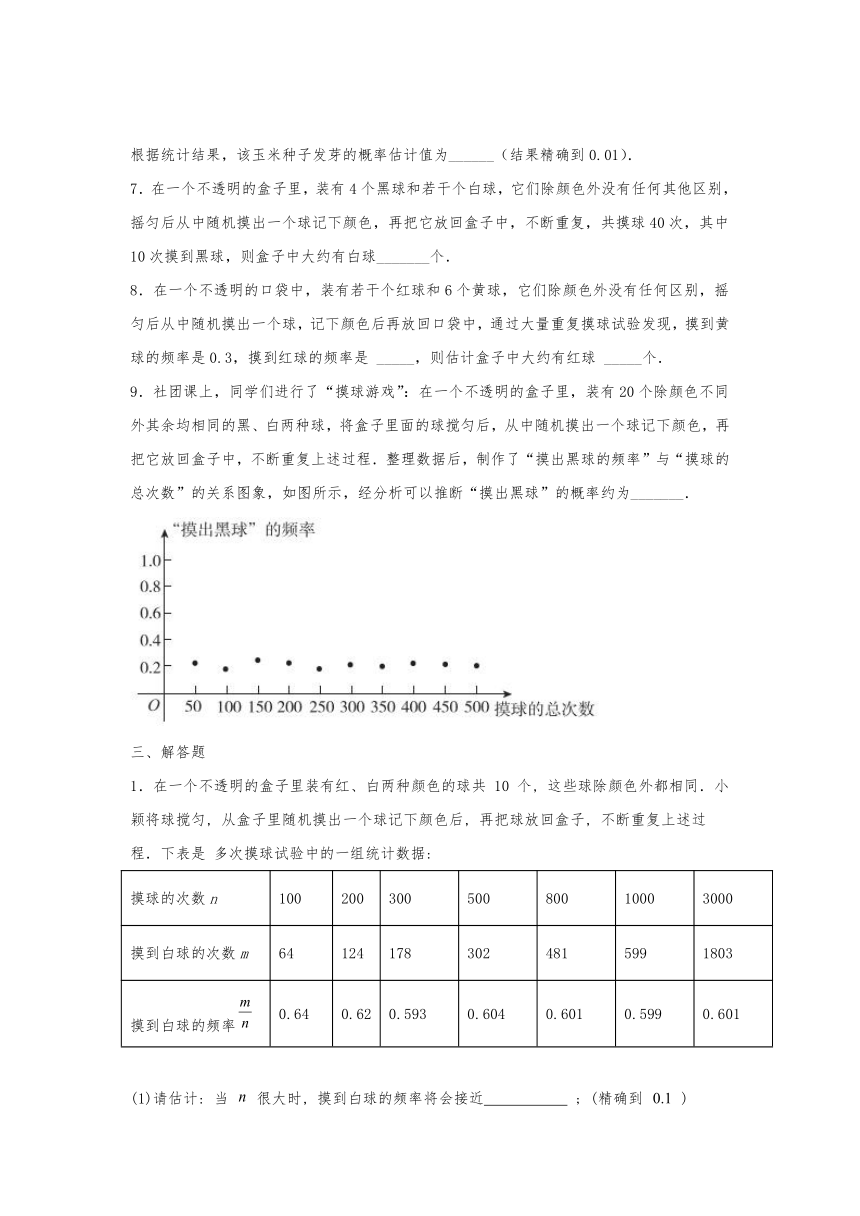
9.社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里,装有20个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后,从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图象,如图所示,经分析可以推断“摸出黑球”的概率约为_______.
三、解答题
1.在一个不透明的盒子里装有红、白两种颜色的球共 10 个, 这些球除颜色外都相同.小颖将球搅匀, 从盒子里随机摸出一个球记下颜色后, 再把球放回盒子, 不断重复上述过程.下表是 多次摸球试验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 64 124 178 302 481 599 1803
摸到白球的频率 0.64 0.62 0.593 0.604 0.601 0.599 0.601
(1)请估计: 当 很大时, 摸到白球的频率将会接近 ; (精确到 )
(2)若从盒子里随机摸出一个球, 求摸到白球的概率的估计值.(精确到 )
2.某水果公司新进一批柑橘,销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.
柑橘总质量n/kg … 300 350 400 450 500
损坏柑橘质量m/kg … 30.93 35.32 40.36 45.02 51.05
柑橘损坏的频率(精确到0.001) … 0.103 0.101 0.101 0.100 0.102
(1)柑橘损坏的概率约为______(精确到0.1);
(2)当抽取柑橘的总质量n=2000kg时,损坏柑橘质量m最有可能是______.
A.99.32kg B.203.45kg C.486.76kg D.894.82kg
(3)若水果公司新进柑橘的总质量为10000kg,成本价是1.8元/kg,公司希望这些柑橘能够获得利润5400元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
3.某种油菜籽在相同条件下的发芽试验的结果如下:
试验的粒数n 20 80 100 200 400 800 1000 1500
发芽的粒数m 14 54 67 132 264 532 670 1000
发芽的频率 0.7 0.675 0.67 0.66 0.66 0.665 a 0.667
(1)填空:上表中a=_________;
(2)根据上表,请估计,当n很大时,发芽的频率将会接近多少?(结果保留两位小数)
(3)根据上表,这种油菜籽发芽的概率的估计值是多少?(结果保留两位小数)
4.为了监控一条生产线某种零件的生产质量,检验员每隔25分钟从该生产线上随机抽取一个零件,并测量其尺寸(单位:毫米).下表是检验员在-一天内抽取的20个零件尺寸的数据统计:
抽取次序 1 2 3 4 5 6 7 8 9 10
零件尺寸 107.5 109.3 108.1 109.3 109.6 108.4 108.5 109.8 108.9 109.0
抽取次序 11 12 13 14 15 16 17 18 19 20
零件尺寸 110.2 109.0 107.8 108.2 109.4 108.4 109.7 108.6 109.1 110.4
记零件尺寸的数据为x,按照生产标准,需对超标零件进行整改,整改费用如下表:
尺寸范围(m为正数) 零件等级 整改费用(元/个)
超标零件 100
合格零件
优等零件
特优零件
优等零件
合格零件
超标零件 80
(1)求所抽取的20个零件出现超标零件的频率;
(2)若从超标零件中随机抽取两件进行整改,求整改费用最低的概率
答案
一、选择题
C.B.C.B.B.A.D.B.A.D.
二、填空题
1.0.6.
2..
3.6.
4.0.25.
5.0.5.
6.0.95.
7.12.
8.0.7,14.
9.0.2.
三、解答题
1.
(1)
解:∵当n=1000时,摸到白球的频率约为0.6,当n=3000时,摸到白球的频率约为0.6,
∴当n很大时,摸到白球的频率将会接近0.6;
故答案为:0.6;
(2)
解:∵当n很大时,摸到白球的频率将会接近0.6,
∴若从盒子里随机摸出一只球,则摸到白球的概率的估计值为0.6;
2.(1)
根据表格信息,柑橘损坏的概率约为0.1,
故答案为:0.1;
(2)
当抽取柑橘总质量n=2000kg时,损坏柑橘质量m约为2000×0.1=200(kg),
故选:B.
(3)
根据柑橘损坏的概率约为0.1,可得能够出售的柑橘为:
(kg)
则定价为:(元)
答:每千克大约定价2.6元比较合适.
3.(1)
解:a=670÷1000= 0.67,
故答案为:0.67;
(2)
当n很大时,发芽的频率将会接近0.67;
(3)
从频率的波动情况可以发现频率稳定在0.67附近,
在相同条件下,当试验次数很大时,事件发生的频率可作为概率的估计值,
所以这种油菜籽发芽的概率的估计值约为0.67.
4.(1)
解:(1)所抽取的20个零件出现超标零件的个数有4个,即107.5、110.2、107.8、110.4,
∴所抽取的20个零件出现超标零件的频率为;
(2)
解:把零件尺寸为107.5毫米、110.2毫米、107.8毫米、110.4毫米的4个零件分别记为A、B、C、D,
画树状图如下:
共有12种等可能的结果,整改费用最低的结果有2种,即BD、DB,
∴整改费用最低的概率为.
一、选择题
1.口袋里有若干个白球,又放进去6个黑球,这些球除颜色外其他均相同,小明每次摸出一个球并记下颜色后放回,多次摸球后发现摸到白球的频率稳定在,则口袋里的白球数很可能为( )
A.4 B.6 C.9 D.15
2.小明为估计一个不规则图案的面积,采取了以下办法:首先用一个面积为10cm2的长方形将不规则图案围起来(如图①);然后在一固定位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在边界线上或长方形区域外不计试验结果);最后将若干次有效试验的结果绘制成了图②所示的折线统计图.请估计不规则图案的面积大约为( )
A.4cm2 B.3.5 cm2 C.4.5 cm2 D.5 cm2
3.下列判断错误的是( )
A.了解一批冰箱的使用寿命,采用抽样调查的方式
B.一组数据2,5,3,5,6,8的众数和中位数都是5
C.甲、乙两组队员身高数据的方差分别为,,那么甲组队员的身高比较整齐
D.一个不透明的袋子里装有红球、蓝球共20个,这些球除颜色外都相同,小红通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数可能是5个
4.如图,小红在一张长为6m,宽为5m的长方形纸上画了一个老虎图案,他想知道该图案的面积大小,于是想了这样一个办法,朝长方形的纸上扔小球,并记录小球落在老虎图案上的次数(球扔在界线上或长方形纸外不计试验结果),他将若干次有效试验的结果整理成统计表,由此他估计此图案的面积大约为( )
试验次数m 60 120 180 240 300 360 420 480
小球落在图案内的次数n 22 38 65 83 102 126 151 168
小球落在图案内的频率 0.37 0.32 0.36 0.35 0.34 0.35 0.36 0.35
A. B. C. D.
5.一只不透明的袋子中装有若干个白球和红球,共计20个,这些球除颜色外都相同.将球搅匀,每次从中随机摸出一个球,记下颜色后放回、再搅匀、再摸球,通过大量重复摸球试验后,发现摸到白球的频率稳定于0.3,由此可估计袋子中红球的个数约为( )
A.6 B.14 C.5 D.20
6.小明在一次用频率估计概率的实验中,从一副去掉大小王的扑克牌中,任意抽取一张,把抽到红桃出现的频率绘制的统计图,则满足题意的统计图是( )
A. B.
C. D.
7.某人在做抛掷硬币试验中,抛掷n次,正面朝上有m次,若正面朝上的频率是P,则下列说法正确的是( )
A.P一定等于0.5 B.多投一次,P更接近0.5
C.P一定不等于0.5 D.投掷次数逐渐增加,P稳定在0.5附近
8.某射击运动员在同一条件下的射击成绩记录如下表所示,根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率 (结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
A.0.90 B.0.82 C.0.85 D.0.84
9.王师傅对某批零件的质量进行了随机抽查,并将抽查结果绘制成如下表格,请你根据表格估计,若从该批零件中任取一个,为合格零件的概率为( )
随机抽取的零件个数 20 50 100 500 1000
合格的零件个数 18 46 91 450 900
零件的合格率 0.9 0.92 0.91 0.9 0.9
A.0.9 B.0.8 C.0.5 D.0.1
10.下列说法错误的是( )
A.太阳从东方升起是必然事件
B.不可能事件发生的概率为0
C.在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值
D.某种彩票中奖的概率是1%,买100张该种彩票一定会中奖
二、填空题
1.如图,是某射手在相同条件下进行射击训练的结果统计图,则该射手击中靶心的概率估计值为__________.(结果精确到0.1)
2.某篮球运动员在罚球线上投篮的结果如下表所示:
投篮次数 50 100 150 200 250 300 500
投中次数m 28 60 78 104 123 152 251
投中频率 0.56 0.60 0.52 0.52 0.49 0.51 0.50
那么估计这名篮球运动员投篮一次投中的概率是________(结果精确到0.01).
3.在一个不透明的袋子中有红球和白球共20个,它们除颜色外都相同.每次从袋中随机摸出一个小球,记下颜色后再放回袋中,通过多次重复实验,发现摸出白球的频率稳定在0.3附近.则估计袋子中的白球有______个.
4.在一个箱子里有若干个黄色和白色的乒乓球,这些乒乓球除颜色外均相同,小明摇匀后从中随机摸出一球,记下颜色后放回;摇匀后再随机摸出一球,记下颜色后放回;不断重复该试验,结果如下图所示,则他随机从箱子里摸出一球摸到黄色乒乓球的概率大约为_____.(结果保留两位小数)
随机摸出的乒乓球数n 100 200 500 1000 2000 3000
摸到黄色乒乓球个数m 26 51 126 251 500 750
摸到黄色乒乓球的频率 0.26 0.255 0.252 0.251 0.25 0.25
5.某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼,鱼塘主通过多次捕捞试验发现,捕捞到鲫鱼的频率稳定在0.25左右.若鱼塘主随机在鱼塘里捕捞一条鱼,捕捞到草鱼的概率约为______.
6.科研人员对某玉米种子在相同条件下的发芽情况进行试验,统计结果如下表:
试验的种子数n(单位:粒) 500 800 1000 2000 3000
发芽的频数m(单位:粒) 458 764 948 1902 2849
发芽的频率 0.916 0.955 0.948 0.9510 0.950
根据统计结果,该玉米种子发芽的概率估计值为______(结果精确到0.01).
7.在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则盒子中大约有白球_______个.
8.在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.3,摸到红球的频率是 _____,则估计盒子中大约有红球 _____个.
9.社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里,装有20个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后,从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图象,如图所示,经分析可以推断“摸出黑球”的概率约为_______.
三、解答题
1.在一个不透明的盒子里装有红、白两种颜色的球共 10 个, 这些球除颜色外都相同.小颖将球搅匀, 从盒子里随机摸出一个球记下颜色后, 再把球放回盒子, 不断重复上述过程.下表是 多次摸球试验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 64 124 178 302 481 599 1803
摸到白球的频率 0.64 0.62 0.593 0.604 0.601 0.599 0.601
(1)请估计: 当 很大时, 摸到白球的频率将会接近 ; (精确到 )
(2)若从盒子里随机摸出一个球, 求摸到白球的概率的估计值.(精确到 )
2.某水果公司新进一批柑橘,销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.
柑橘总质量n/kg … 300 350 400 450 500
损坏柑橘质量m/kg … 30.93 35.32 40.36 45.02 51.05
柑橘损坏的频率(精确到0.001) … 0.103 0.101 0.101 0.100 0.102
(1)柑橘损坏的概率约为______(精确到0.1);
(2)当抽取柑橘的总质量n=2000kg时,损坏柑橘质量m最有可能是______.
A.99.32kg B.203.45kg C.486.76kg D.894.82kg
(3)若水果公司新进柑橘的总质量为10000kg,成本价是1.8元/kg,公司希望这些柑橘能够获得利润5400元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
3.某种油菜籽在相同条件下的发芽试验的结果如下:
试验的粒数n 20 80 100 200 400 800 1000 1500
发芽的粒数m 14 54 67 132 264 532 670 1000
发芽的频率 0.7 0.675 0.67 0.66 0.66 0.665 a 0.667
(1)填空:上表中a=_________;
(2)根据上表,请估计,当n很大时,发芽的频率将会接近多少?(结果保留两位小数)
(3)根据上表,这种油菜籽发芽的概率的估计值是多少?(结果保留两位小数)
4.为了监控一条生产线某种零件的生产质量,检验员每隔25分钟从该生产线上随机抽取一个零件,并测量其尺寸(单位:毫米).下表是检验员在-一天内抽取的20个零件尺寸的数据统计:
抽取次序 1 2 3 4 5 6 7 8 9 10
零件尺寸 107.5 109.3 108.1 109.3 109.6 108.4 108.5 109.8 108.9 109.0
抽取次序 11 12 13 14 15 16 17 18 19 20
零件尺寸 110.2 109.0 107.8 108.2 109.4 108.4 109.7 108.6 109.1 110.4
记零件尺寸的数据为x,按照生产标准,需对超标零件进行整改,整改费用如下表:
尺寸范围(m为正数) 零件等级 整改费用(元/个)
超标零件 100
合格零件
优等零件
特优零件
优等零件
合格零件
超标零件 80
(1)求所抽取的20个零件出现超标零件的频率;
(2)若从超标零件中随机抽取两件进行整改,求整改费用最低的概率
答案
一、选择题
C.B.C.B.B.A.D.B.A.D.
二、填空题
1.0.6.
2..
3.6.
4.0.25.
5.0.5.
6.0.95.
7.12.
8.0.7,14.
9.0.2.
三、解答题
1.
(1)
解:∵当n=1000时,摸到白球的频率约为0.6,当n=3000时,摸到白球的频率约为0.6,
∴当n很大时,摸到白球的频率将会接近0.6;
故答案为:0.6;
(2)
解:∵当n很大时,摸到白球的频率将会接近0.6,
∴若从盒子里随机摸出一只球,则摸到白球的概率的估计值为0.6;
2.(1)
根据表格信息,柑橘损坏的概率约为0.1,
故答案为:0.1;
(2)
当抽取柑橘总质量n=2000kg时,损坏柑橘质量m约为2000×0.1=200(kg),
故选:B.
(3)
根据柑橘损坏的概率约为0.1,可得能够出售的柑橘为:
(kg)
则定价为:(元)
答:每千克大约定价2.6元比较合适.
3.(1)
解:a=670÷1000= 0.67,
故答案为:0.67;
(2)
当n很大时,发芽的频率将会接近0.67;
(3)
从频率的波动情况可以发现频率稳定在0.67附近,
在相同条件下,当试验次数很大时,事件发生的频率可作为概率的估计值,
所以这种油菜籽发芽的概率的估计值约为0.67.
4.(1)
解:(1)所抽取的20个零件出现超标零件的个数有4个,即107.5、110.2、107.8、110.4,
∴所抽取的20个零件出现超标零件的频率为;
(2)
解:把零件尺寸为107.5毫米、110.2毫米、107.8毫米、110.4毫米的4个零件分别记为A、B、C、D,
画树状图如下:
共有12种等可能的结果,整改费用最低的结果有2种,即BD、DB,
∴整改费用最低的概率为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
