湘教版数学八年级上册 2.5 全等三角形的判定 复习课 教案
文档属性
| 名称 | 湘教版数学八年级上册 2.5 全等三角形的判定 复习课 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 191.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 08:03:14 | ||
图片预览

文档简介
《全等三角形的判定复习课》教学设计
教学内容:新湘教版八年级上册第2单元第5小节《全等三角形的判定》
教学目标:
熟练掌握全等三角形的判定方法。
能准确、灵活的运用三角形全等的判定方法解决问题。
3、通过变式练习提高分析问题和解决问题的能力。训练学生解题的严谨性。
重、难点:
重点:利用三角形全等的判定方法正确的解题。
难点:能准确、灵活的运用三角形全等的判定方法解决问题。
教法学法:讲练结合、小组合作
教学手段;多媒体辅助教学
教学过程:
一、解读目标(2分钟)
采用了课前将学习目标写在导学案上,课上让学生先齐读,教师再解析的方法来完成。
在这个环节中,让学生通过齐读,教师解读目标的过程在课的开始就明确本节课的学习目标及学习的重、难点,带着目标进行学习,为学生指明了学习的方向。
二、自主学习(6分钟)
知识点梳理:
能够 两个三角形叫做全等三角形;
全等三角形的对应边 ,对应角 ;
三角形全等的判定方法(简写) 、 、 、 ;
的两个直角三角形全等,简写为 。
简单应用(如图1所示):
由DE=DG, 、DF=DF根据SAS
可以判定△DEF≌△DGF;
由 、DE=DG、 根据ASA
可以判定△DEF≌△DGF;
由 、∠E=∠G、DE=DG,根据AAS
可以判定△DEF≌△DGF;
由DE=DG、 、 根据SSS
可以判定△DEF≌△DGF;
由∠E=∠G=90°、DF=DF、 根据HL可以判定Rt△DEF≌Rt△DGF。
对这9个小问题的思考与解答,学生既能回顾学过的三角形全等的几种判定方法,又能通过图形明确三角形全等的具体条件。
三、合作探究
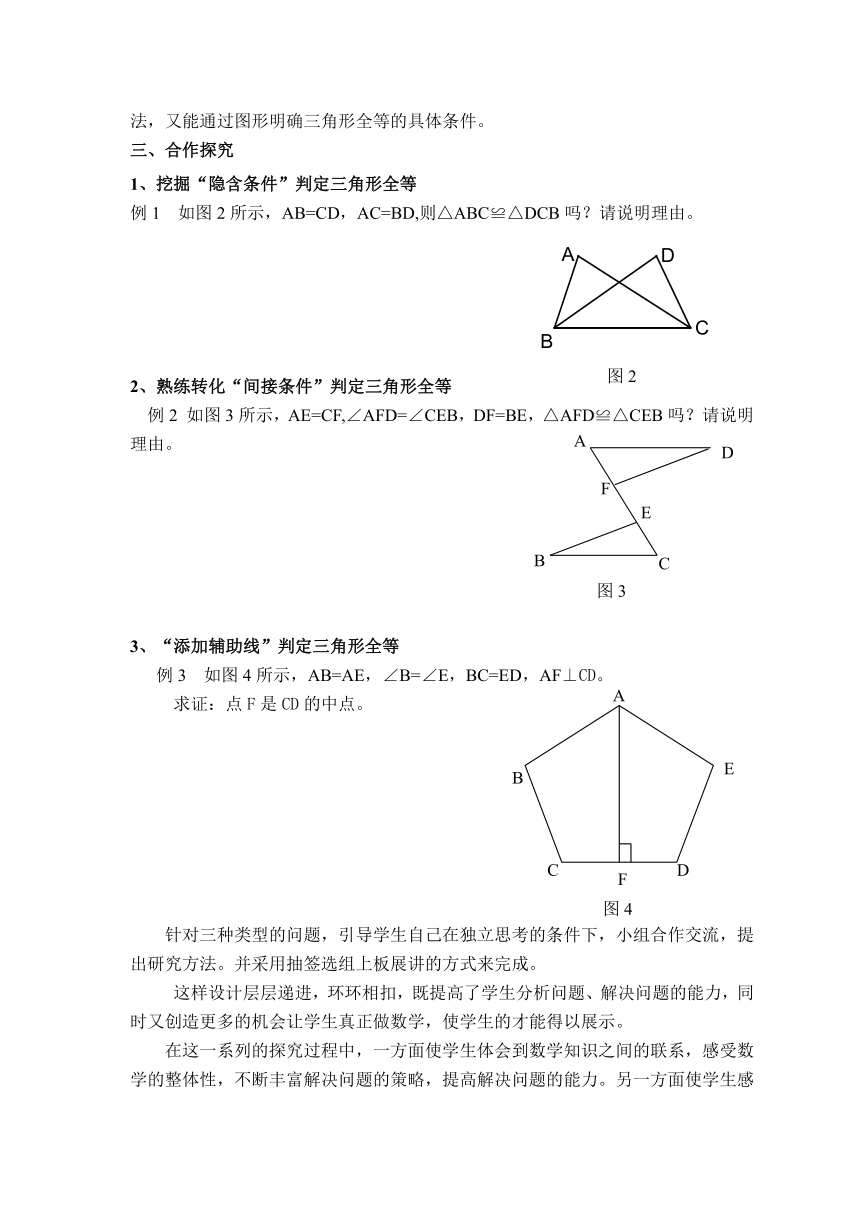
挖掘“隐含条件”判定三角形全等
例1 如图2所示,AB=CD,AC=BD,则△ABC≌△DCB吗?请说明理由。
熟练转化“间接条件”判定三角形全等
例2 如图3所示,AE=CF,∠AFD=∠CEB,DF=BE,△AFD≌△CEB吗?请说明理由。
“添加辅助线”判定三角形全等
例3 如图4所示,AB=AE,∠B=∠E,BC=ED,AF⊥CD。
求证:点F是CD的中点。
针对三种类型的问题,引导学生自己在独立思考的条件下,小组合作交流,提出研究方法。并采用抽签选组上板展讲的方式来完成。
这样设计层层递进,环环相扣,既提高了学生分析问题、解决问题的能力,同时又创造更多的机会让学生真正做数学,使学生的才能得以展示。
在这一系列的探究过程中,一方面使学生体会到数学知识之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解决问题的能力。另一方面使学生感受到全等图形的无限魅力,体会到数学的美,激发学生学习数学的热情。
四、实战训练
五、小结归纳
通过本节课的学习你有什么收获?
总结点评(5分钟)
指导学生在判定三角形全等,找全等条件时要注意对“隐含条件”,如公共边、公共角、对顶角等条件的挖掘;注意对“间接条件”的转化;以及如何恰当的添加“辅助线”。
六、课后作业
1.如图所示,若OB=OD,∠A=∠C,AB=3cm,则CD= ,请说明理由。
2.如图所示,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC≌△ADE吗?请说明理由。
作业:必做题:完成课本第87页第3,4,5题
选做题:课本第88页第11,12题
课后反思:教学内容接近尾声,老师要引导学生进行反思与交流,总结归纳这节课所研究的知识、思想、方法,个人收获,存在问题,鼓励学生及时发现问题并提出问题,既体现了知识的连续性,同时又体现了因材施教的原则,使学生得到全面发展,同时教师进行自我教学评价,总结得失,使教学更有益于学生发展.
作业分为必做和选做.学生来自不同的家庭,个人情况不尽相同,这样既肯定了学生的差异,又满足了不同学生的需求,体现了因材施教的原则.
总之,经历观察、猜想、论证、应用的全过程,不仅使学生理解了三角形全等的判定,更重要的是让学生学会观察,学会思考,更加深刻地体会了从具体到抽象,从特殊到一般的辩证唯物主义观点,让学生在学习过程中欣赏数学,探索数学,会学数学.
E
F
D
G
图1
图2
F
CC
B
E
A
D
图3
F
E
D
CA
B
A
图4
1. (2018安顺5题)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD
( )
A. ∠B=∠C B. AD=AE
C. BD=CE D. BE=CD
2. (2014铜仁21题10分)如图所示,已知∠1=∠2,请你添加一个条件,
证明:AB=AC.
(1)你添加的条件是________________;
(2)请写出证明过程.
3. (2018铜仁20题10分)已知,如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.
求证:AE∥FB.
4. (2016铜仁20题10分)如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上.
求证:DE=DF.
O
B
A
D
CA
E
B
D
C
A
教学内容:新湘教版八年级上册第2单元第5小节《全等三角形的判定》
教学目标:
熟练掌握全等三角形的判定方法。
能准确、灵活的运用三角形全等的判定方法解决问题。
3、通过变式练习提高分析问题和解决问题的能力。训练学生解题的严谨性。
重、难点:
重点:利用三角形全等的判定方法正确的解题。
难点:能准确、灵活的运用三角形全等的判定方法解决问题。
教法学法:讲练结合、小组合作
教学手段;多媒体辅助教学
教学过程:
一、解读目标(2分钟)
采用了课前将学习目标写在导学案上,课上让学生先齐读,教师再解析的方法来完成。
在这个环节中,让学生通过齐读,教师解读目标的过程在课的开始就明确本节课的学习目标及学习的重、难点,带着目标进行学习,为学生指明了学习的方向。
二、自主学习(6分钟)
知识点梳理:
能够 两个三角形叫做全等三角形;
全等三角形的对应边 ,对应角 ;
三角形全等的判定方法(简写) 、 、 、 ;
的两个直角三角形全等,简写为 。
简单应用(如图1所示):
由DE=DG, 、DF=DF根据SAS
可以判定△DEF≌△DGF;
由 、DE=DG、 根据ASA
可以判定△DEF≌△DGF;
由 、∠E=∠G、DE=DG,根据AAS
可以判定△DEF≌△DGF;
由DE=DG、 、 根据SSS
可以判定△DEF≌△DGF;
由∠E=∠G=90°、DF=DF、 根据HL可以判定Rt△DEF≌Rt△DGF。
对这9个小问题的思考与解答,学生既能回顾学过的三角形全等的几种判定方法,又能通过图形明确三角形全等的具体条件。
三、合作探究
挖掘“隐含条件”判定三角形全等
例1 如图2所示,AB=CD,AC=BD,则△ABC≌△DCB吗?请说明理由。
熟练转化“间接条件”判定三角形全等
例2 如图3所示,AE=CF,∠AFD=∠CEB,DF=BE,△AFD≌△CEB吗?请说明理由。
“添加辅助线”判定三角形全等
例3 如图4所示,AB=AE,∠B=∠E,BC=ED,AF⊥CD。
求证:点F是CD的中点。
针对三种类型的问题,引导学生自己在独立思考的条件下,小组合作交流,提出研究方法。并采用抽签选组上板展讲的方式来完成。
这样设计层层递进,环环相扣,既提高了学生分析问题、解决问题的能力,同时又创造更多的机会让学生真正做数学,使学生的才能得以展示。
在这一系列的探究过程中,一方面使学生体会到数学知识之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解决问题的能力。另一方面使学生感受到全等图形的无限魅力,体会到数学的美,激发学生学习数学的热情。
四、实战训练
五、小结归纳
通过本节课的学习你有什么收获?
总结点评(5分钟)
指导学生在判定三角形全等,找全等条件时要注意对“隐含条件”,如公共边、公共角、对顶角等条件的挖掘;注意对“间接条件”的转化;以及如何恰当的添加“辅助线”。
六、课后作业
1.如图所示,若OB=OD,∠A=∠C,AB=3cm,则CD= ,请说明理由。
2.如图所示,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC≌△ADE吗?请说明理由。
作业:必做题:完成课本第87页第3,4,5题
选做题:课本第88页第11,12题
课后反思:教学内容接近尾声,老师要引导学生进行反思与交流,总结归纳这节课所研究的知识、思想、方法,个人收获,存在问题,鼓励学生及时发现问题并提出问题,既体现了知识的连续性,同时又体现了因材施教的原则,使学生得到全面发展,同时教师进行自我教学评价,总结得失,使教学更有益于学生发展.
作业分为必做和选做.学生来自不同的家庭,个人情况不尽相同,这样既肯定了学生的差异,又满足了不同学生的需求,体现了因材施教的原则.
总之,经历观察、猜想、论证、应用的全过程,不仅使学生理解了三角形全等的判定,更重要的是让学生学会观察,学会思考,更加深刻地体会了从具体到抽象,从特殊到一般的辩证唯物主义观点,让学生在学习过程中欣赏数学,探索数学,会学数学.
E
F
D
G
图1
图2
F
CC
B
E
A
D
图3
F
E
D
CA
B
A
图4
1. (2018安顺5题)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD
( )
A. ∠B=∠C B. AD=AE
C. BD=CE D. BE=CD
2. (2014铜仁21题10分)如图所示,已知∠1=∠2,请你添加一个条件,
证明:AB=AC.
(1)你添加的条件是________________;
(2)请写出证明过程.
3. (2018铜仁20题10分)已知,如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.
求证:AE∥FB.
4. (2016铜仁20题10分)如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上.
求证:DE=DF.
O
B
A
D
CA
E
B
D
C
A
同课章节目录
