九年级数学下册试题 二次函数复习题--最值问题-北师大版(含答案)
文档属性
| 名称 | 九年级数学下册试题 二次函数复习题--最值问题-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 08:55:03 | ||
图片预览



文档简介
二次函数复习题--最值问题
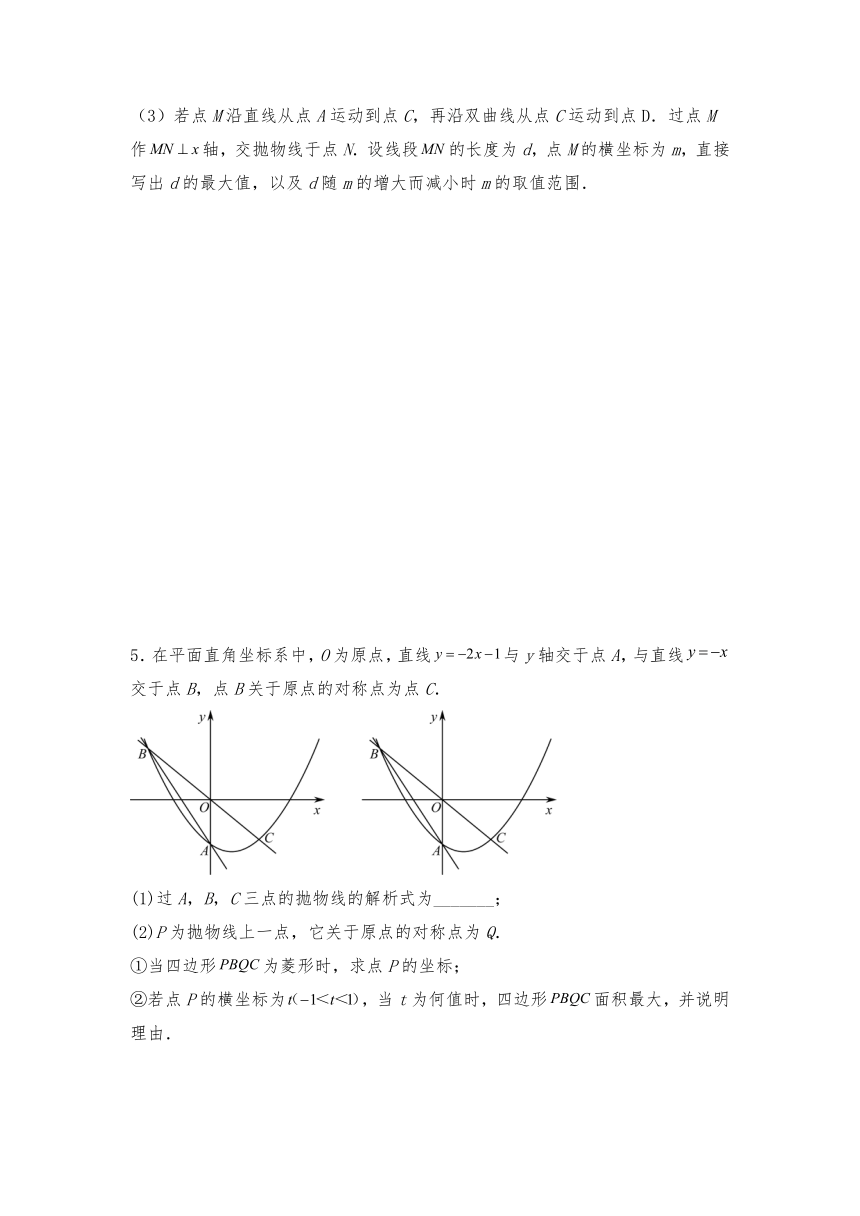
1.已知抛物线,其顶点为,与轴交于点.
(1)求抛物线的解析式;
(2)若直线:与抛物线第一象限交于点,交轴于点,求的值;
(3)若有两个定点,,请在抛物线上找一点,使得的周长最小,并求出周长的最小值.
2.已知抛物线(a,b为常数,)与x轴交于点,顶点为D,且过点.
(1)求抛物线解析式和点C,D的坐标;
(2)点P在该抛物线上(与点B,C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求的面积的最大值;
②连接BD,当时,求点P的坐标.
3.已知:如图,是等腰直角三角形,,动点P,Q同时从A,B两点出发,分别沿,方向匀速移动,P的速度是,Q的速度是,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为,解答下列问题:
(1)当t为何值时,是直角三角形?
(2)问:是否存在某一时刻t,使四边形的面积与面积差最小?如果存在,求出相应的t值;不存在,说明理由;
(3)设的长为,试确定y与t之间的关系式;写出当t分别为何值时,达到最短和最长,并写出的最小值和最大值.
4.如图,在平面直角坐标系中,直线分别交x轴、y轴于点A、点B,交双曲线于点抛物线过点B,且与该双曲线交于点D,点D的纵坐标为.
(1)求双曲线与抛物线的解析式.
(2)若点P为该抛物线上一点,点Q为该双曲线上一点,且P,Q两点的纵坐标都为,求线段的长.
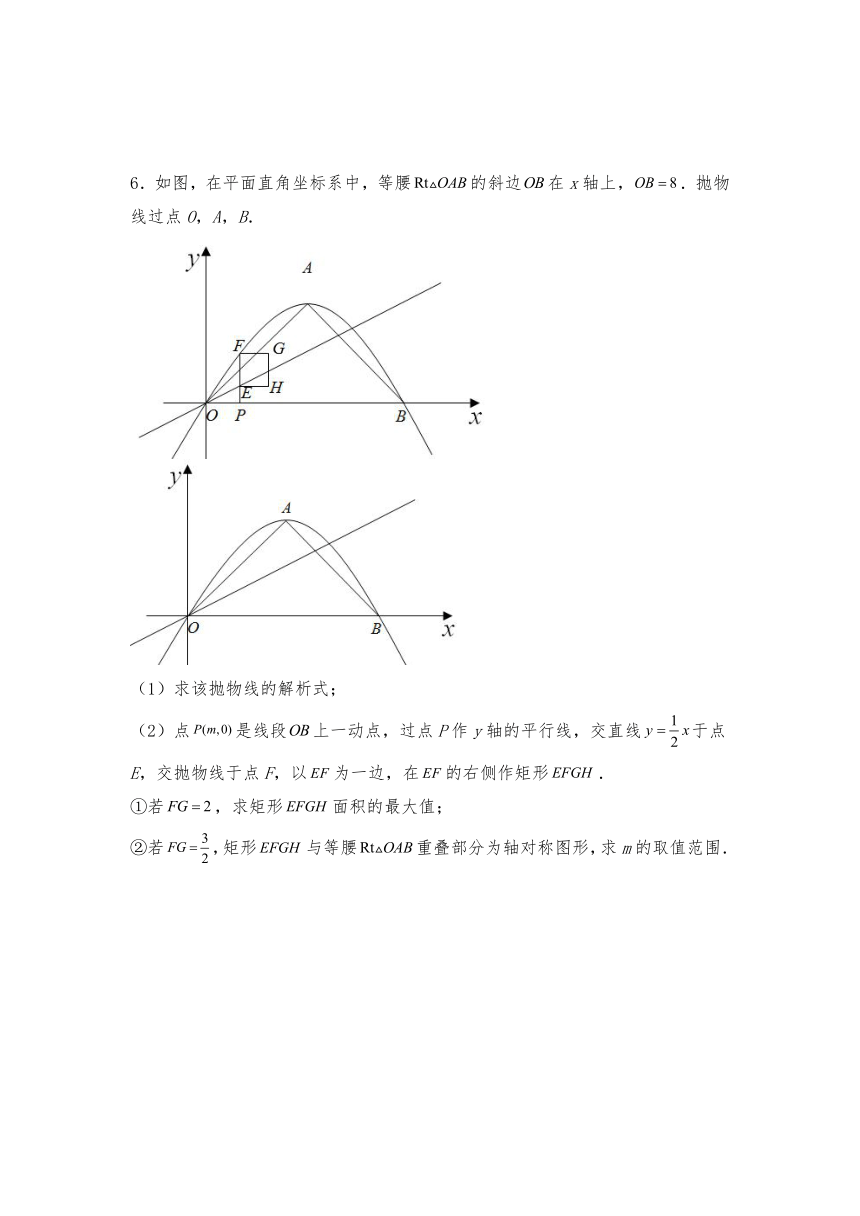
(3)若点M沿直线从点A运动到点C,再沿双曲线从点C运动到点D.过点M作轴,交抛物线于点N.设线段的长度为d,点M的横坐标为m,直接写出d的最大值,以及d随m的增大而减小时m的取值范围.
5.在平面直角坐标系中,O为原点,直线与y轴交于点A,与直线交于点B,点B关于原点的对称点为点C.
(1)过A,B,C三点的抛物线的解析式为_______;
(2)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形为菱形时,求点P的坐标;
②若点P的横坐标为,当t为何值时,四边形面积最大,并说明理由.
6.如图,在平面直角坐标系中,等腰的斜边在x轴上,.抛物线过点O,A,B.
(1)求该抛物线的解析式;
(2)点是线段上一动点,过点P作y轴的平行线,交直线于点E,交抛物线于点F,以为一边,在的右侧作矩形.
①若,求矩形面积的最大值;
②若,矩形与等腰重叠部分为轴对称图形,求m的取值范围.
7.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
8.如图,抛物线(t>0)与x轴的交点为B,A(点B在左边),过线段OA的中点M作MPx轴,交直线(x>0)于点P.
(1)当t=3时,直线MP于抛物线对称轴之间的距离为______;当直线MP于抛物线对称轴距离为3时,t=______.
(2)把抛物线在直线MP左侧部分的图像(含与直线MP的交点)记为,用t表示最高点的坐标.
(3)在(2)的条件下,当t>4时,图像的最高点与P之间的距离何时有最大值,并求出最大值.
9.如图1,抛物线y=ax2+bx+c经过A(﹣2,0)、B(8,0)、C(0,4)三点,顶点为D,连结AC,BC.
(1)求抛物线的函数表达式及顶点D的坐标;
(2)判断三角形ABC的形状,并说明理由;
(3)如图2,点P是该抛物线在第一象限内上的一点.
①过点P作y轴的平行线交BC于点E,若CP=CE,求点P的坐标;
②连结AP交BC于点F,求的最大值.
10.在平面直角坐标系中,O是坐标原点,直角梯形AOCD的顶点A的坐标为(0,),点D的坐标为(1,),点C在x轴的正半轴上,过点O且以点D为顶点的抛物线经过点C,点P为CD的中点.
(1)求抛物线的解析式及点P的坐标;
(2) 在y轴右侧的抛物线上是否存在点Q,使以Q为圆心的圆同时与y轴、直线OP相切.若存在,请求出满足条件的点Q的坐标;若不存在,请说明理由;
(3)点M为线段OP上一动点(不与O点重合),过点O、M、D的圆与y轴的正半轴交于点N.求证:OM+ON为定值.
(4)在y轴上找一点H,使∠PHD最大.试求出点H的坐标.
11.已知:如图1,抛物线的顶点为,平行于轴的直线与该抛物线交于点,(点在点左侧),根据对称性恒为等腰三角形,我们规定:当为直角三角形时,就称为该抛物线的“完美三角形”.
(1)①如图2,求出抛物线的“完美三角形”斜边的长;
②抛物线与的完美三角形的斜边长的数量关系是______;
(2)若抛物线的“完美三角形”的斜边长为4,求的值;
(3)若抛物线的“完美三角形”斜边长为,且的最大值为1,求,的值.
12.在平面直角坐标系中,规定:抛物线的伴随直线为.例如:抛物线的伴随直线为,即.
(1)在上面规定下,抛物线的顶点为 ,伴随直线为 ;
(2)若顶点在第一象限的抛物线与其伴随直线相交于点A,B(点A在点B的左侧),抛物线与x轴交于点C、D(点C在点D的左侧).
①若求的值;
②如果点是直线BC上方抛物线的一个动点,的面积记为S,当S取得最大值时,求的值.
13.如图1,正方形中,点P为对角线BD上一动点,点E在AD的延长线上,且.
(1)填空:PE的长为______;
(2)如图2,过点P作于点F,交DC于点H,延长FP交AB于点G,求证:;
(3)若点E在直线AD上运动,直线PE与直线CD交于点M,其他条件不变,则PM的长为______;
(4)若点P为正方形对角线BD上的动点,则的最小值为______.
14.如图,抛物线与轴交于,两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交轴于点,在该抛物线的对称轴上是否存在点,使得的周长最小?若存在,求出点的坐标;若不存在,请说明理由.
(3)在(1)中的抛物线上的第二象限上是否存在一点,使的面积最大?若存在,求出面积的最大值.若没有,请说明理由.
15.已知抛物线(b、c为常数),若此抛物线与某直线相交于,两点,与y轴交于点N,其顶点为D
(1)求抛物线的函数解析式和顶点D的坐标;
(2)若点P是抛物线上位于直线上方的一个动点,求的面积的最大值及此时点P的坐标;
(3)点为抛物线上的一个动点,H关于y轴的对称点为,当点落在第二象限内,且取得最小值时,求n的值
16.如图1,抛物线与x轴交于点,与y轴交于点C,点P为x轴上方抛物线上的动点,点F为y轴上的动点,连接PA,PF,AF.
(1)求该抛物线所对应的函数解析式;
(2)如图1,当点F的坐标为,求出此时△AFP面积的最大值;
(3)如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.
17.对于平面直角坐标系xOy中的点P,Q,给出如下定义:若P,Q为某个三角形的顶点,且边PQ上的高h,满足h=PQ,则称该三角形为点P,Q的“完美三角形”.
(1)如图1,已知点A,B在x轴上,点C在y轴上,AB=3,BC=6,∠OBC=30°,试判断△ABC是否是点A,B的“完美三角形”,并说明理由;
(2)如图2,已知A(4,0),点B在x轴上,点C在直线y=2x﹣5上,若Rt△ABC是点A,B的“完美三角形”,求点B的坐标;
(3)已知直线y=x+2与抛物线y=x2交于R,S两点,点M是线段RS下方抛物线上的一个动点,点N是坐标平面内一点,△RSN为点R,S的“完美三角形”,直接写出M,N两点之间距离的最小值.
18.如图,已知抛物线的解析式为,抛物线与x轴交于点A和点B,与y轴交点于点C.
(1)请分别求出点A、B、C的坐标和抛物线的对称轴;
(2)连接AC、BC,将△ABC绕点B顺时针旋转90°,点A、C的对应点分别为M、N,求点M、N的坐标;
(3)若点为该抛物线上一动点,在(2)的条件下,请求出使最大时点的坐标,并请直接写出的最大值.
19.正方形ABCD边长为2,点E、F在CB、DC延长线上,且BE=CF,AE 与BF延长线交于点G.
(1)如图1,求证AE⊥BF;
(2)如图2,点M是FG延长线上一点,MG=BG,∠MAD的平分线交BF于点N,连接CN.试探究AN、CN、BN三条线段的数量关系,并证明;
(3)如图3,G为BC上一点,过G作GH⊥DG交AB于H点,当BG=____,BH达到最大值,最大值是____ .
20.如图,已知抛物线的图象与x轴交于点A(1,0),B(-3,0),与y轴的正半轴交于点C.
(1)求该抛物线的解析式;
(2)点D是线段上一动点,过点D作y轴的平行线,与交于点E,与抛物线交于点F.
①连接,当的面积最大时,求此时点F的坐标;
②探究是否存在点D使得为直角三角形?若存在,求出点F的坐标;若不存在,说明理由.
21.如图,在平面直角坐标系中,O为坐标原点,AD为等腰△ABC底边BC上的高,抛物线的顶点为点A,且经过B、C两点,已知直线AB的解析式为y=x+2
(1)求该抛物线的解析式;
(2)点E为抛物线上位于直线AC上方的一点,过点E作EN⊥x轴交直线AC于点N,点M(5,b)是抛物线上的一点,点P为对称轴上一动点,当线段EN的长度最大时,求PE+PM的最小值.
(3)点H是射线BA上的一个动点,过点D作DH的垂线交射线AC于点G,过点G作OC的垂线交抛物线于点F,直接写出H点坐标为何值时, CG的长为,并写出此时点F的坐标.
22.抛物线交轴于,两点在的左边),交轴于,直线经过,两点.
(1)求抛物线的解析式;
(2)如图1,点M在抛物线上,点在抛物线的对称轴上,以点A、C、M、N为顶点,AC为边的的四边形是平行四边形,请求出所有符合条件的点N的坐标.
(3)如图2,为直线上方的抛物线上一点,y轴交于点,过点作于点.设,求的最大值;
23.在平面直角坐标系xOy中,已知抛物线与x轴交于A、B两点,OB=3OA,与y轴交于C点,对称轴是x=1,D为抛物线顶点.
(1)求抛物线的表达式和点D的坐标.
(2)连接AD,交y轴于点E,P是抛物线上的一个动点.Q是抛物线对称轴上一个点,是否存在以B,E,P,Q为顶点的四边形为平行四边形,若存在,求出P点坐标;若不存在,请说明理由.
(3)如图,点P在第四象限的抛物线上,连接AP、BE交于点G,设,则w有最大值还是最小值?w的最值是多少?
(4)已知点C和M关于抛物线对称轴对称,点N在直线BC上运动,求的最小值 .
答案
1.解:(1)将点代入得:,解得,
;
(2)由题意得:
解得:或,
结合题意可得:
顶点 而
,故,
连接并延长至点,使,
则是的中垂线,连接交轴于点,
由中点公式可得:点,则,
则,
设为:
则,
解得:,
所以直线的函数表达式为:,故点,
在中,,,,
过点作与点,设:,则,
则,
解得:,则,故,
即:;
(3)作直线,交轴于点,过点作直线交于点,连接,
则点,设点,
则,
则,而,即,
而(点位于点时取等号),
故的最小值为,而,
故周长的最小值为:.
2.(1)解:把点,点代入,
可得:,解得
∴抛物线解析式为,
,
∴顶点.
把代入在,得,
∴点.
(2)解:由题意可知点P坐标为,
①如图,过点P作轴于点H,交直线BC于点E,
设直线BC的解析式为,将,点代入,
得,解得.
∴直线BC的解析式为.
∵点P的坐标为,由题意可知,
∴点E的坐标为.
∴.
∴
.
∵,
∴当时,的面积的最大值为.
②存在.
如图①,当点P在直线BC的上方,且时,则,
设直线DB的解析式为,将,点代入,
得,解得.
∴直线BD的解析式为.
∵,
∴设直线PC的解析式为.
∵,
∴.
∴.
∴直线PC的解析式为.
∴.
解得,(舍).
当时,.
∴点P的坐标为.
如图②,当点P在直线BC的下方时,设直线PC与BD交于点M,
∵,
∴.
设,
∵,
,
∴
解得.
∴点M的坐标为.
由点和点可得直线CM的解析式为,
由,
解得,(舍).
所以点.
综上,点P的坐标为或.
3.解:(1)由题可得:,,,,.
①当时,如图1,
,
,
.
,
解得:;
②当时,如图2,
同理可得:,
,
解得:;
综上所述;当为1或时,是直角三角形.
(2)分两种情况:
①当时,作于,如图3所示:
,
是等腰直角三角形,
,
的面积,
四边形的面积的面积的面积,
四边形的面积的面积,当时,面积差最小,
但是,不符合题意;
②当时,作于,如图4所示:
,
是等腰直角三角形,
,
的面积,
四边形的面积的面积的面积,
四边形的面积的面积,
当时,面积差最小;
因此,存在某一时刻,使四边形的面积与面积差最小,;
(3)根据题意得:时,存在的值,使最短,;理由如下:
如图3所示:,,
由勾股定理得:,
∴y=,
当时,y的最小值,
当时,;
当时,;
综上所述:当时,最短,最小值;
当到达时,恰好到达,此时秒,的最大值.
4.解:(1)令,则,
解得,
令,则,
所以,点,,
时,,
所以,点,
设双曲线解析式为,
则,
解得,
所以,双曲线解析式为,
点的纵坐标为,
,
解得,
点,
抛物线过点、,
,
解得,
抛物线的解析式为;
(2)当时,,
整理得,,
解得,,
点的坐标为,或,,
,
解得,
点的坐标为,
或;
(3)①点在上时,,
,
随的增大而减小,
②点在上时,,
,
时,有最大值为,
时,随的增大而减小,
③点在上时,,
,
由图可知,随的增大而减小,
综上所述,的最大值是,,,时,随的增大而减小.
5.(1)
解:联立两直线解析式可得,
解得,
点坐标为,
又点为点关于原点的对称点,
点坐标为,
直线与轴交于点,
点坐标为,
设抛物线解析式为,
把、、三点坐标代入可得,
解得,
抛物线解析式为,
故答案为:;
(2)
①当四边形为菱形时,则,
直线解析式为,
直线解析式为,
联立抛物线解析式可得,
解得或,
点坐标为,或,;
②当时,四边形的面积最大.
理由如下:
如图,过作,垂足为,作轴的垂线,交直线于点,
则,
线段长固定不变,
当最大时,四边形面积最大,
又(固定不变),
当最大时,也最大,
点在抛物线上,点在直线上,
点坐标为,点坐标为,
,
当时,有最大值1,此时有最大值,即四边形的面积最大.
6.解:(1)过点A作AD⊥x轴于D
∵等腰的斜边在x轴上,,
∴OD=DB==4,点B的坐标为(8,0)
∴AD==4
∴点A的坐标为(4,4)
由抛物线过点O,A,B,设抛物线的解析式为
将点A的坐标代入,得
解得:
∴抛物线的解析式为;
(2)①设抛物线与直线的右交点为C,
联立
解得:或
∴点C的坐标为(6,3)
当0≤m<6时,如下图所示,
∴点E的坐标为(m,),点F的坐标为(m,)
∴EF=-=
∴S矩形EFGH=FG·EF==
∵<0
∴当m=3时,S矩形EFGH有最大值,最大值为;
当6≤m≤8时,如下图所示
∴点E的坐标为(m,),点F的坐标为(m,)
∴EF=-=
∴S矩形EFGH=FG·EF==,对应抛物线的开口向上,对称轴为直线m=3,
∴在对称轴右侧,y随x的增大而增大
∵6≤m≤8
∴当m=8时,S矩形EFGH有最大值,最大值为8;
∵<8
∴矩形面积的最大值为8;
②(i)当矩形的四个顶点都在抛物线对称轴左侧时,如下图所示,此时,m+≤4,即m≤,
若矩形与等腰重叠部分为轴对称图形,易知此时四边形为正方形
∴EF=FG
∴=
解得:m1=,m2=(不符合前提,舍去)
∴此时m=;
(ii)当矩形的四个顶点中,E、F在抛物线对称轴左侧、G、H在抛物线对称轴右侧时,如下图所示,此时,m≤4且m+>4,即<m≤4,
若矩形与等腰重叠部分为轴对称图形,易知此时抛物线的对称轴直线x=4也是矩形的对称轴
∴此时点E的横坐标m=4-FG=;
(iii)当矩形的四个顶点都在抛物线对称轴右侧,且H在AB左侧时,如下图所示,矩形与等腰重叠部分为直角梯形,不可能是轴对称图形,不符合题意,舍去;
(iiii)当点H落在AB上时,设直线与AB交于点M,
∵EH∥OB
∴∠EHA=∠OBA=45°
∴矩形与等腰重叠部分为等腰直角三角形,即为轴对称图形
∴此时符合题意
设直线AB的解析式为y=kx+b
将点A、B的坐标代入,得
解得:
∴直线AB的解析式为y=-x+8
由点E(m,)
∴点H的坐标为(m+,),代入y=-x+8中,得
=-(m+)+8
解得:m=
联立
解得:
∴点M的坐标为(,)
由下图可知:从点H落在AB上到点E与点M重合之前,矩形与等腰重叠部分为等腰直角三角形,即为轴对称图形
∴此时符合题意
∴≤m<;
(iiiii)当m≥,即点E和点M重合或点E在点M右侧时,如下图所示,矩形与等腰无重叠部分,故不符合题意,舍去;
综上:m=或m=或≤m<.
7.解:(1)将A(﹣1,0),C(2,3)代入y=﹣x2+bx+c,得:
,解得:,
∴抛物线的函数关系式为y=﹣x2+2x+3.
设直线AC的函数关系式为y=kx+a(k≠0),
将A(﹣1,0),C(2,3)代入y=kx+a,得:
,解得:,
∴直线AC的函数关系式为y=x+1.
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴点D的坐标为(1,4).
当x=1时,y=x+1=2,
∴点B的坐标为(1,2).
设点E的坐标为(x,x+1).
分两种情况考虑(如图1):
①当点E在线段AC上时,点F在点E上方,
∴点F的坐标为(x,x+3).
∵点F在抛物线上,
∴x+3=﹣x2+2x+3,
解得:x1=0,x2=1(舍去),
∴点E的坐标为(0,1);
②当点E在线段AC(或CA)延长线上时,点F在点E下方,
∴点F的坐标为(x,x﹣1).
∵点F在抛物线上,
∴x﹣1=﹣x2+2x+3,
解得:,
∴点E的坐标为()或(,).
综上:满足条件的点E的坐标为(0,1),()或(,).
(3)过点P作PM⊥x轴,垂足为点M,过点C作CN⊥x轴,垂足为N,如图2所示.
设点P的坐标为(x,﹣x2+2x+3)(﹣1<x<2),则点M的坐标为(x,0).
∵点A的坐标为(﹣1,0),点C的坐标为(2,3),
∴AM=x+1,MN=2﹣x,PM=﹣x2+2x+3,CN=3,AN=3,
∴S△APC=S△APM+S梯形PMNC﹣S△ACN,
.
∴当x=时,S△APC取得最大值,最大值为,此时点P的坐标为().
8.解:(1)时,=,
当y=0时,解得x1=3,x2=-1,
∴
∴
直线MP:
∵对称轴
∴距离为.
= ,
当y1=0时,解得x1=t,x2=-t-4,
∴
∴
∴直线MP:.
对称轴:.
∵,
∴,
∴.
(2)直线MP:
对称轴:
①当,时
,
∴坐标为
②当,时
,
∴坐标为
③当,时
,
∴坐标为
综上所述:04时,(,);
(3)t>4时,最高点D坐标为
P点坐标为
∴无最大值
9.(1)设抛物线的解析式为y=a(x+2)(x﹣8).
∵抛物线经过点C(0,4),
∴﹣16a=4,解得a=﹣.
∴抛物线的解析式为y=﹣(x+2)(x﹣8)=x2+x+4.
∵A(﹣2,0)、B(8,0),
∴抛物线的对称轴为x=3.
∵将x=3代入得:y=,
∴抛物线的顶点D坐标为(3,).
(2)三角形ABC是直角三角形,理由如下:
∵AB=10,AC=2,BC=4,
∴AC2+BC2=AB2.
∴∠BCA=90°,所以三角形ABC是直角三角形.
(3) ①如图1所示:作CM⊥PE,垂足为M.
设直线BC的解析式为y=kx+b.
∵将B、C的坐标代入得:,解得k=﹣,b=4,
∴直线BC的解析式为y=﹣x+4.
设点P(m,﹣ m2+m+4),则点E(m,﹣ m+4),M(m,4).
∵PC=EC,CM⊥PE,
∴PM=EM.
∴﹣m2+m+4﹣4=4﹣(﹣m+4),解得:m=0(舍去),m=4.
∴P(4,6).
②作PN⊥BC,垂足为N.
由①得:PE=﹣m2+2m.
∵PE∥y轴,PN⊥BC,
∴∠PNE=∠COB=90°,∠PEN=∠BCO.
∴△PNE∽△BOC.
∴=.
∴PN=PE=(﹣m2+2m).
由(2)知∠BCA=90°,
又∵∠PFN=∠CFA,
∴△PFN∽△CAF.
∴=﹣m2+m.
∴当m=4时,的最大值为.
10.解:(1)∵抛物线的顶点D的坐标为(1,),
∴设抛物线的解析式为y=a(x 1)2+,
将(0,0)代入,得a+=0,a= ,
∴抛物线的解析式为y= (x 1)2+,
即 y= x2+2x,
设y=0,则x=0或2,
∴点C的坐标为(0,2),
∵点P为CD的中点,
∴;
(2)在y轴右侧的抛物线上存在点Q,使以Q为圆心的圆同时与y轴、直线OP相切,
理由如下:
①若⊙Q在直线OP上方,则Q与D点重合,此时Q1(1,);
②若⊙Q在直线OP下方,与y轴、直线OP切于E、F,
则QE=QF,QE⊥y轴,QF⊥OP,
∴OQ平分∠EOF,
∵∠EOF=120°,
∴∠FOQ=60°,
∵∠POC=30°,则∠QOC=30°,
设Q(m, m),则 m= m2+2m,
解得m1=0(舍去),m2=,
∴Q2(, );
(3)证明:∵在过点O、M、D的圆中,有∠MOD=∠NOD,
∴,
∴MD=ND,
易得OD平分∠AOP,DA⊥y轴,DP⊥OP,
∴DA=DP,
可证得△NAD≌△MPD(HL),
∴MP=AN,
∴OM+ON=OP MP+OA+AN=OP+OA=2OA=,
则OM+ON=2,即OM+ON为定值;
(4)作过P、D两点且与y轴相切于点H的圆S,
则由圆周角大于圆外角可知,∠PHD最大.
设S(x,y),则由HS=SD=SP,
可得,y=2±6,
∵0<y<,
∴H(0,2 6).
11.(1)①过点作轴于,
∵△AMB为等腰直角三角形,
∴∠ABM=45°,
∵AB∥x轴,
∴∠BMN=∠ABM=45°,
∴∠MBN=90°-45°=45°,
∴∠BMN=∠MBN,
∴MN=BN,
设点坐标为,代入抛物线,得,
∴,(舍去),
∴MN=BN=1,
∴
∴
在Rt△AMB中,
∴抛物线的“完美三角形的斜边
②∵抛物线y=x2+1与y=x2的形状相同,
∴抛物线y=x2+1与y=x2的“完美三角形”的斜边长的数量关系是相等;
故答案为:相等.
(2)∵抛物线与抛物线的形状相同,
∴抛物线与抛物线的完美三角形”全等,
∵抛物线的“完美三角形”斜边的长为4,∴抛物线的“完美三角形”斜边的长为4,
∴点坐标为或,∴.
(3)∵的最大值为-1,
∴,
∴,
∵抛物线的“完美三角形”斜边长为,
抛物线的“完美三角形”斜边长为,
∴点坐标为,
∴代入抛物线,得,
∵n>0
∴,
∴,
∴
12.(1)抛物的顶点坐标为(-1,-4),伴随直线为,即,
故答案为:(-1,-4);;
(2)当时,有,
解得:,
∴点C的坐标为(-1,0),点D的坐标为(3,0).
抛物线的伴随直线为,即,
联立,
解得:,,
①∵A(1,-4m),B(2,-3m),C(-1,0),
∴,
,
.
∵∠CAB=90°,
∴,即,
解得:,(不合题意,舍去),
∴m的值为;
②过点P作PE∥y轴,交直线AC于点E,如图所示.
设直线BC的解析式为(k≠0),
将点B(2,-3m)、C(-1,0)代入,得:
,解得:,
∴直线AC的解析式为.
设点P的坐标为,则点Q的坐标为(,),
∵P是直线BC上方抛物线上的一个动点,
∴,
∴S=,
∴当时,△PBC的面积有最大值,
依题意得:,
∴.
13.(1)
解:如图,过点P作于点F,
∵点P在正方形对角线BD上,
∴∠ADP=45°,
∵,,
∴,
∴,
在Rt△中,根据勾股定理得:
,
(2)
证明:∵,,
∴
∴,
如图,作于点I,
得到矩形,矩形,
∴GI=AD,BG=CI,
∴AD=CD=GI,
∵GI=CD,∠GIC=∠CDE=90°,
∴△HIG≌△DEC(AAS),
∴HI=DE,
∴CI=CH+HI=CH+DE,
∴BG=CH+DE.
(3)
当点M在CD边上时,过点PN⊥AD于点N,
∴PNDM,
∴△EDM∽△ENP,
∴,
由(1)得:,
∴,
∴;
当点在CD延长线上时,作于点O,
由(1)知:AO=NO=2,
∵,
∴,
∵,ON=DN,,
∴△≌△(ASA),
∴,
∴,
综上:PM的长为或
(4)
点P为正方形ABCD对角线BD上的动点,
∴BD=,
∴,
∴当时,的最小值为36.
14.(1)
解:将,代入中,
可得:,
解得:,
∴抛物线的解析式为:;
(2)
解:存在,理由如下:
如图,
∵、两点关于抛物线的对称轴对称,
∴直线与的交点即为点,此时周长最小,连接、,
∵点是抛物线与轴的交点,
∴的坐标为,
又∵,
∴直线解析式为:,
∴点坐标即为,
解得:,
∴;
(3)
解:存在,理由如下:
如图,设,过点作轴交于点,连接、、,
∵,
若有最大值,则就最大,
∴,
∵,
又∵,
∴,
∴,
∴,
∴当时,最大值为.
15.(1)
∵将点A和点C的坐标代入抛物线的解析式得:,解得:.
∴抛物线的解析式为 .
∴
∴抛物线的顶点坐标为,
(2)
设直线的解析式为.
∵将点A和点C的坐标代入得,解得.
∴直线的解析式为.
如图,
设点 ,
∴,
∴ =,
∴
,
∴当m时,, ,
∴P(,);
(3)
∵落在第二象限内,H关于y轴的对称点为
∴点在第一象限,即n>0,t>0.
∵抛物线的顶点坐标为(1,4),
∴ ,
∵在抛物线上,
∴ ,
∴ ,
∵,,
∴= = = =;
∴当t时,有最小值,即有最小值,
∴ ,解得或,
∵ ,
∴不合题意,舍去,
∴n的值为.
16.(1)
解:∵抛物线与x轴交于点,
∴ ,
解得:,
∴该抛物线所对应的函数解析式为;
(2)
如图1,过点P作PQy轴交直线AF于点Q,
设直线AF的解析式为,
∵,
∴,
解得:,
∴直线AF的解析式为,
设,则Q,
∴,
∴,
∵<0,,
∴当t时,△AFP面积的最大值为;
(3)
设P(m,)(),F(0,n),
∵A(3,0),
∴OA3,OF|n|,
①当APAF,∠PAF90°时,如图2,过点P作PD⊥x轴于点D,
则∠ADP90°∠AOF,
∴∠PAD+∠APD90°,
∵∠PAD+∠FAO90°,
∴∠APD∠FAO,
在△APD和△FAO中,
,
∴△APD≌△FAO(AAS),
∴PDOA,ADOF,
∵PD,AD,OA,
∴,
解得:m0或2,
当m0时,P(0,3),AD3,
∴OF3,即|n|3,
∵点F在y的负半轴上,
∴,
∴F;
当m2时,P(2,3),AD1,
∴OF=1,即|n|1,
∵点F在y的负半轴上,
∴,
∴F(0,);
②当APPF,∠APF90°时,如图3,过点P作PD⊥x轴于点D,PG⊥y轴于点G,
则∠PDA∠PDO∠PGF90°,
∵∠PDO∠PGF∠DOG90°,
∴四边形PDOG是矩形,
∴∠FPG+∠FPD90°,
∵∠APD+∠FPD∠APF90°,
∴∠FPG∠APD,
在△FPG和△APD中,
,
∴△FPG≌△APD(AAS),
∴PGPD,FGAD,
∵PD,AD3﹣m,PGm,
∴m,
解得: (舍去), ,
当m=时,P(,),
∴=,
∴F(0,);
综上所述,点F的坐标为(0,)或(0,)或(0,).
17.(1)
解:∵∠BOC=90°,∠OBC=30°,
∴COBC,
∵BC=6,
∴CO=3,
又∵AB=3,
∴CO=AB即△ABC的边AB上的高等于AB,
∴△ABC是点A,B的“完美三角形”;
(2)
分A、B、C为直角顶点讨论:
①若C为直角顶点,如答图1,
则∠ACB=90°,作CH⊥AB于H,取AB中点M,
根据Rt△ABC是点A,B的“完美三角形”得AB=CH,
∵M为AB中点,∠ACB=90°,
∴CMAB,
CH⊥AB于H有CM≥CH,
∴AB≥AB得AB≤0,这和AB为线段矛盾,
故C不可能为直角顶点;
②若A为直角顶点,如答图2,过A作y轴平行线交直线y=2x﹣5于C,
∵A(4,0),
∴C点横坐标=4,代入y=2x﹣5得C纵坐标=3,即AC=3,
∵Rt△ABC是点A,B的“完美三角形”,
∴AB=3,
∴(1,0)或(7,0);
③若B为直角顶点,如答图3,过B作y轴平行线交直线y=2x﹣5于C,
设B(m,0),则C(m,2m﹣5),
∴BC=|2m﹣5|,
而A(4,0),故AB=|4﹣m|,
∵Rt△ABC是点A,B的“完美三角形”,
∴BC=AB,即|2m﹣5|=|4﹣m|,
由2m﹣5=4﹣m得m=3,此时(3,0),
由2m﹣5=m﹣4得m=1,此时(1,0);
综上所述,Rt△ABC是点A,B的“完美三角形”,(1,0)或(7,0)或(3,0);
(3)
由得,,
如答图4,
∴R(﹣1,1),S(2,4),
∴RS=3,
∵△RSN为点R,S的“完美三角形”,
∴N到RS的距离为3,
令y=x+2中y=0可得x=﹣2,即直线y=x+2与x轴交点D(﹣2,0),
过D作DE⊥RS,在垂线上取DE=3,(注:点M是线段RS下方抛物线上的一个动点,且M,N两点之间距离的最小值,故E应在D右侧)
∵直线y=x+2与x轴夹角∠ODR=45°,
∴∠ODE=45°,
过E作EFRS交x轴于F,则△DEF是等腰直角三角形,
∵DE=3,
∴DF=6,
∴F(4,0),
设EF解析式为y=x+b,将F(4,0)代入可得EF为y=x﹣4,
即N点在直线y=x﹣4上,且直线y=x﹣4与y轴交点P(0,﹣4)
∵线段RS下方抛物线上的一个动点M到EF距离最近,
∴将直线y=x﹣4平移至与抛物线只有一个交点时,此交点即为M,
设此时直线为y=x+c,
由联立方程只有一个交点,
得,即,
可得c,即直线MN为y=x,
∴直线MN与y轴交点G(0,),过G作GH⊥EF于H,则△GHP是等腰直角三角形,且GP,
∴GH,
∴M,N两点之间距离的最小值是,
故答案为:.
18.(1)
解:∵,
令x=0,则y=3,
令y=0,则,
解得x=-4或1,
∴A(-4,0),B(1,0),C(0,3),
∵,
∴对称轴为直线x=-;
(2)
解:如图所示:
过N作NQ⊥x轴于点Q,
由旋转性质得MB⊥x轴,∠CBN=90°,BM=AB=5,BN=BC,
∴M(1,5),∠OBC+∠QBN=90°,
∵∠OBC+∠BCO=90°,
∴∠BCO=∠QBN,
又∵∠BOC=∠NQB=90°,BN=BC,
∴△OBC≌△QNB(AAS),
∴BQ=OC=3,NQ=OB=1,
∴OQ=1+3=4,
∴N(4,1);
(3)
解:设直线NB的解析式为y=kx+b.
∵B(1,0)、N(4,1)在直线NB上,
∴,
解得:,
∴直线NB的解析式为:y=x-,
当点P,N,B在同一直线上时|NP-BP|=NB=,
当点P,N,B不在同一条直线上时|NP-BP|<NB,
∴当P,N,B在同一直线上时,|NP-BP|的值最大,
即点P为直线NB与抛物线的交点.
解方程组:,
解得:或,
∴当P的坐标为(1,0)或时,|NP-BP|的值最大,此时最大值为.
19.(1)
解:证明:如图1,
四边形是正方形,
,,,
,,
,
,
,
,
,
,
.
(2)
,
证明:如图2,连接,作交于点,
,,
,,
,,
,
,
,
,
,,
,
,
,
,
,
,
,
.
(3)
如图3,设,,
,
,
,
,
,
,
,
,
,
当时,,
当,达到最大值,最大值是,
故答案为:1,.
20.(1)
解:将点A(1,0)、B( 3,0)代入y=,
得:,
解得:
∴二次函数解析式为.
(2)
①令x=0,代入,得:,
∴C(0,3),
∵B(-3,0),
∴设直线BC的解析式为y=kx+b,代入得
,
解得:,
∴直线BC的解析式为:y=x+3
设F(x,),则E(x,x+3)
∴FE=-(x+3)=,
∴的面积=()=,
∴x=-时,的面积最大,此时F(-,);
②Ⅰ当∠CFE=90°时,如图:
∵DFy轴,
∴DF⊥x轴,
∴∠ODF=∠CFE=90°,
∴CFOB,
∴点F的纵坐标为3,
∴3=﹣﹣2x+3,
解得=0(舍去),=﹣2,
∴F(﹣2,3),
Ⅱ当∠ECF=90°时,过点C作CH⊥EF于H,
∵DFy轴,
∴DF⊥x轴,
∴∠BDE=90°,
∵C(0,3),B(﹣3,0),
∴OC=OB=3,
∴∠OBC=45°,
∴∠OEB=∠CEH=45°,
∵∠ECF=90°,
∴CE=CF,
∵CH⊥EF,
∴EF=2CH,
设D(m,0),则E(m,m+3),F(m,),
∴EF=﹣(m+3)=﹣﹣3m,CH=﹣m,
∴﹣﹣3m=﹣m,
∴=0(舍去),=﹣1,
∴点D坐标为(﹣1,0).
∴F(﹣1,4)
综上,点F的坐标为(﹣2,3)或(﹣1,4).
21.(1)
∵抛物线的顶点为A,
∴.A的横坐标为2,
又∵直线AB的解析式为
∴当时,,当时,
∴点A的坐标为(2,4),B(,0)
将(2,4),(,0)代入得:,
∴抛物线的解析式为.
(2)
由(1)得:
∵对称轴为直线,B(,0)
设E(t,),N(t,)
∴当时,EN最大为1
∴E(4,3)
∵AD是此抛物线的对称轴
∴过点E作AD的对称点(0,3),连接交AD于点P,此时最短,M(5,)
(3)
如图①所示:
设GF交x轴于点E,在中,,,
∴,
∴,
将代入抛物线的解析式可得:,
∴点F的坐标为(3,)
在与中,
∴,
又∵点A的坐标为(2,4)
∴H的坐标为(1,3);
同理如图②所示,
在中,,,
∴,
∴,
将代入抛物线的解析式可得:,
∴F的坐标为(7,),
在与中,
∴,
又∵点A的坐标为(2,4)
∴H的坐标为(3,5);
综上所述,H(1,3),点F(3,)或H(3,5),F(7,).
22.(1)
解:当时,;
当时,,;
,,
点,在抛物线上,
,解得:,
;
(2)
当以AC为边时,点N的坐标为(,);当以AC为对角线时,点N的坐标为(,);
∵抛物先线的函数表达式:,
∴抛物线的对称轴为:x=,
当y=0时,,解得:x=-3或x=4,
∴点A(-3,0),
设点N(,n),点M(m,),
①当AN为平行四边形的边时,AM和CN为对角线,
,解得:,
∴N(,)
②当AM为平行四边形的边时,AN和CM为对角线,
,解得:
∴N(,),
综上:点N的坐标为:(,)或(,).
(3)
如图1,连接,延长交轴于,
轴,
轴,
设,,
,
,且,,,
,
,
,
∵,
∴,
当时,有最大值是,
23.(1)
解:∵OB=3OA,
∴设A(-β,0),则B(3β,0),
∵对称轴是x=1,
∴=1,
∴β=1,
∴A(-1,0),B(3,0),
∴,解得:,
∴抛物线的表达式为,
当x=1时,y=1-2-3=-4,
∴点D的坐标为(1,4);
(2)
解:∵A(-1,0),B(3,0),D (1,4),
设直线AD的表达式为y=kx+c,
∴,解得,
∴直线AD的表达式为y=-2x-2,
当x=0时,y=-2,
∴点E的坐标为(0,-2),
∵P是抛物线上的一个动点,Q是抛物线对称轴上一个点,
∴设P(m,),Q(1,t),
①当BE为边时,PQBE且PQ=BE,
当E对应Q,由(0,-2)变为(1,t),要向右平移1个单位,
则当B(3,0)对应P(m,),也要向右平移1个单位,即m=3+1=4,
∴=5,
∴P(4,5);
当E对应P,B对应Q,由(3,0)变为(1,t),向左平移2个单位,
则由(0,-2)变为(m,),也向左平移2个单位,
∴m=0-2=-2,
∴m2-2m-3=5,
∴P(-2,5);
②当BE为对角线时,BE的中点坐标为(,),即(,),
∴PQ的中点坐标也为(,),
∴=,∴m=2,则=-3,
∴P(2,-3);
综上,点P的坐标为(4,5)或(-2,5)或(2,-3);
(3)
解:∵点P在第四象限的抛物线上,AP、BE交于点G,
设P(m,),其中0<m<3,
设直线AP的表达式为y=cx+d,
∵A(-1,0),P(m,),
∴,解得:,
∴直线AP的表达式为y=(m-3)x+m-3,
同理求得直线BE的表达式为y=x-2,
联立方程组,得:,
解得:,
∴,
∵0<m<3,
∴24-8m>0,3m-11<0,
∴,
∴
令,
∵-3<0,
∴当m=时,z取得最大值,w取得最小值为,
∴w有最小值,最小值为.
(4)
解:当x=0时,y=-3,
∴点C的坐标为(0,-3),
∵点B的坐标为(3,0),
∴OB=3,OC=3,
∴△OBC是等腰直角三角形,
∴∠OBC=∠OCB=45°,
同理求得直线BC的表达式为y=x-3,
∵点C和M关于抛物线对称轴对称,
∴点M的坐标为(2,-3),
过点N作NH⊥x轴于点H,
∵∠OBC=45°,
∴△BHN是等腰直角三角形,
∴HN=BN,
∴,
∴当M、N、H在同一直线上时,取得最小值,
∴的最小值为3.
故答案为:3.
1.已知抛物线,其顶点为,与轴交于点.
(1)求抛物线的解析式;
(2)若直线:与抛物线第一象限交于点,交轴于点,求的值;
(3)若有两个定点,,请在抛物线上找一点,使得的周长最小,并求出周长的最小值.
2.已知抛物线(a,b为常数,)与x轴交于点,顶点为D,且过点.
(1)求抛物线解析式和点C,D的坐标;
(2)点P在该抛物线上(与点B,C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求的面积的最大值;
②连接BD,当时,求点P的坐标.
3.已知:如图,是等腰直角三角形,,动点P,Q同时从A,B两点出发,分别沿,方向匀速移动,P的速度是,Q的速度是,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为,解答下列问题:
(1)当t为何值时,是直角三角形?
(2)问:是否存在某一时刻t,使四边形的面积与面积差最小?如果存在,求出相应的t值;不存在,说明理由;
(3)设的长为,试确定y与t之间的关系式;写出当t分别为何值时,达到最短和最长,并写出的最小值和最大值.
4.如图,在平面直角坐标系中,直线分别交x轴、y轴于点A、点B,交双曲线于点抛物线过点B,且与该双曲线交于点D,点D的纵坐标为.
(1)求双曲线与抛物线的解析式.
(2)若点P为该抛物线上一点,点Q为该双曲线上一点,且P,Q两点的纵坐标都为,求线段的长.
(3)若点M沿直线从点A运动到点C,再沿双曲线从点C运动到点D.过点M作轴,交抛物线于点N.设线段的长度为d,点M的横坐标为m,直接写出d的最大值,以及d随m的增大而减小时m的取值范围.
5.在平面直角坐标系中,O为原点,直线与y轴交于点A,与直线交于点B,点B关于原点的对称点为点C.
(1)过A,B,C三点的抛物线的解析式为_______;
(2)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形为菱形时,求点P的坐标;
②若点P的横坐标为,当t为何值时,四边形面积最大,并说明理由.
6.如图,在平面直角坐标系中,等腰的斜边在x轴上,.抛物线过点O,A,B.
(1)求该抛物线的解析式;
(2)点是线段上一动点,过点P作y轴的平行线,交直线于点E,交抛物线于点F,以为一边,在的右侧作矩形.
①若,求矩形面积的最大值;
②若,矩形与等腰重叠部分为轴对称图形,求m的取值范围.
7.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
8.如图,抛物线(t>0)与x轴的交点为B,A(点B在左边),过线段OA的中点M作MPx轴,交直线(x>0)于点P.
(1)当t=3时,直线MP于抛物线对称轴之间的距离为______;当直线MP于抛物线对称轴距离为3时,t=______.
(2)把抛物线在直线MP左侧部分的图像(含与直线MP的交点)记为,用t表示最高点的坐标.
(3)在(2)的条件下,当t>4时,图像的最高点与P之间的距离何时有最大值,并求出最大值.
9.如图1,抛物线y=ax2+bx+c经过A(﹣2,0)、B(8,0)、C(0,4)三点,顶点为D,连结AC,BC.
(1)求抛物线的函数表达式及顶点D的坐标;
(2)判断三角形ABC的形状,并说明理由;
(3)如图2,点P是该抛物线在第一象限内上的一点.
①过点P作y轴的平行线交BC于点E,若CP=CE,求点P的坐标;
②连结AP交BC于点F,求的最大值.
10.在平面直角坐标系中,O是坐标原点,直角梯形AOCD的顶点A的坐标为(0,),点D的坐标为(1,),点C在x轴的正半轴上,过点O且以点D为顶点的抛物线经过点C,点P为CD的中点.
(1)求抛物线的解析式及点P的坐标;
(2) 在y轴右侧的抛物线上是否存在点Q,使以Q为圆心的圆同时与y轴、直线OP相切.若存在,请求出满足条件的点Q的坐标;若不存在,请说明理由;
(3)点M为线段OP上一动点(不与O点重合),过点O、M、D的圆与y轴的正半轴交于点N.求证:OM+ON为定值.
(4)在y轴上找一点H,使∠PHD最大.试求出点H的坐标.
11.已知:如图1,抛物线的顶点为,平行于轴的直线与该抛物线交于点,(点在点左侧),根据对称性恒为等腰三角形,我们规定:当为直角三角形时,就称为该抛物线的“完美三角形”.
(1)①如图2,求出抛物线的“完美三角形”斜边的长;
②抛物线与的完美三角形的斜边长的数量关系是______;
(2)若抛物线的“完美三角形”的斜边长为4,求的值;
(3)若抛物线的“完美三角形”斜边长为,且的最大值为1,求,的值.
12.在平面直角坐标系中,规定:抛物线的伴随直线为.例如:抛物线的伴随直线为,即.
(1)在上面规定下,抛物线的顶点为 ,伴随直线为 ;
(2)若顶点在第一象限的抛物线与其伴随直线相交于点A,B(点A在点B的左侧),抛物线与x轴交于点C、D(点C在点D的左侧).
①若求的值;
②如果点是直线BC上方抛物线的一个动点,的面积记为S,当S取得最大值时,求的值.
13.如图1,正方形中,点P为对角线BD上一动点,点E在AD的延长线上,且.
(1)填空:PE的长为______;
(2)如图2,过点P作于点F,交DC于点H,延长FP交AB于点G,求证:;
(3)若点E在直线AD上运动,直线PE与直线CD交于点M,其他条件不变,则PM的长为______;
(4)若点P为正方形对角线BD上的动点,则的最小值为______.
14.如图,抛物线与轴交于,两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交轴于点,在该抛物线的对称轴上是否存在点,使得的周长最小?若存在,求出点的坐标;若不存在,请说明理由.
(3)在(1)中的抛物线上的第二象限上是否存在一点,使的面积最大?若存在,求出面积的最大值.若没有,请说明理由.
15.已知抛物线(b、c为常数),若此抛物线与某直线相交于,两点,与y轴交于点N,其顶点为D
(1)求抛物线的函数解析式和顶点D的坐标;
(2)若点P是抛物线上位于直线上方的一个动点,求的面积的最大值及此时点P的坐标;
(3)点为抛物线上的一个动点,H关于y轴的对称点为,当点落在第二象限内,且取得最小值时,求n的值
16.如图1,抛物线与x轴交于点,与y轴交于点C,点P为x轴上方抛物线上的动点,点F为y轴上的动点,连接PA,PF,AF.
(1)求该抛物线所对应的函数解析式;
(2)如图1,当点F的坐标为,求出此时△AFP面积的最大值;
(3)如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.
17.对于平面直角坐标系xOy中的点P,Q,给出如下定义:若P,Q为某个三角形的顶点,且边PQ上的高h,满足h=PQ,则称该三角形为点P,Q的“完美三角形”.
(1)如图1,已知点A,B在x轴上,点C在y轴上,AB=3,BC=6,∠OBC=30°,试判断△ABC是否是点A,B的“完美三角形”,并说明理由;
(2)如图2,已知A(4,0),点B在x轴上,点C在直线y=2x﹣5上,若Rt△ABC是点A,B的“完美三角形”,求点B的坐标;
(3)已知直线y=x+2与抛物线y=x2交于R,S两点,点M是线段RS下方抛物线上的一个动点,点N是坐标平面内一点,△RSN为点R,S的“完美三角形”,直接写出M,N两点之间距离的最小值.
18.如图,已知抛物线的解析式为,抛物线与x轴交于点A和点B,与y轴交点于点C.
(1)请分别求出点A、B、C的坐标和抛物线的对称轴;
(2)连接AC、BC,将△ABC绕点B顺时针旋转90°,点A、C的对应点分别为M、N,求点M、N的坐标;
(3)若点为该抛物线上一动点,在(2)的条件下,请求出使最大时点的坐标,并请直接写出的最大值.
19.正方形ABCD边长为2,点E、F在CB、DC延长线上,且BE=CF,AE 与BF延长线交于点G.
(1)如图1,求证AE⊥BF;
(2)如图2,点M是FG延长线上一点,MG=BG,∠MAD的平分线交BF于点N,连接CN.试探究AN、CN、BN三条线段的数量关系,并证明;
(3)如图3,G为BC上一点,过G作GH⊥DG交AB于H点,当BG=____,BH达到最大值,最大值是____ .
20.如图,已知抛物线的图象与x轴交于点A(1,0),B(-3,0),与y轴的正半轴交于点C.
(1)求该抛物线的解析式;
(2)点D是线段上一动点,过点D作y轴的平行线,与交于点E,与抛物线交于点F.
①连接,当的面积最大时,求此时点F的坐标;
②探究是否存在点D使得为直角三角形?若存在,求出点F的坐标;若不存在,说明理由.
21.如图,在平面直角坐标系中,O为坐标原点,AD为等腰△ABC底边BC上的高,抛物线的顶点为点A,且经过B、C两点,已知直线AB的解析式为y=x+2
(1)求该抛物线的解析式;
(2)点E为抛物线上位于直线AC上方的一点,过点E作EN⊥x轴交直线AC于点N,点M(5,b)是抛物线上的一点,点P为对称轴上一动点,当线段EN的长度最大时,求PE+PM的最小值.
(3)点H是射线BA上的一个动点,过点D作DH的垂线交射线AC于点G,过点G作OC的垂线交抛物线于点F,直接写出H点坐标为何值时, CG的长为,并写出此时点F的坐标.
22.抛物线交轴于,两点在的左边),交轴于,直线经过,两点.
(1)求抛物线的解析式;
(2)如图1,点M在抛物线上,点在抛物线的对称轴上,以点A、C、M、N为顶点,AC为边的的四边形是平行四边形,请求出所有符合条件的点N的坐标.
(3)如图2,为直线上方的抛物线上一点,y轴交于点,过点作于点.设,求的最大值;
23.在平面直角坐标系xOy中,已知抛物线与x轴交于A、B两点,OB=3OA,与y轴交于C点,对称轴是x=1,D为抛物线顶点.
(1)求抛物线的表达式和点D的坐标.
(2)连接AD,交y轴于点E,P是抛物线上的一个动点.Q是抛物线对称轴上一个点,是否存在以B,E,P,Q为顶点的四边形为平行四边形,若存在,求出P点坐标;若不存在,请说明理由.
(3)如图,点P在第四象限的抛物线上,连接AP、BE交于点G,设,则w有最大值还是最小值?w的最值是多少?
(4)已知点C和M关于抛物线对称轴对称,点N在直线BC上运动,求的最小值 .
答案
1.解:(1)将点代入得:,解得,
;
(2)由题意得:
解得:或,
结合题意可得:
顶点 而
,故,
连接并延长至点,使,
则是的中垂线,连接交轴于点,
由中点公式可得:点,则,
则,
设为:
则,
解得:,
所以直线的函数表达式为:,故点,
在中,,,,
过点作与点,设:,则,
则,
解得:,则,故,
即:;
(3)作直线,交轴于点,过点作直线交于点,连接,
则点,设点,
则,
则,而,即,
而(点位于点时取等号),
故的最小值为,而,
故周长的最小值为:.
2.(1)解:把点,点代入,
可得:,解得
∴抛物线解析式为,
,
∴顶点.
把代入在,得,
∴点.
(2)解:由题意可知点P坐标为,
①如图,过点P作轴于点H,交直线BC于点E,
设直线BC的解析式为,将,点代入,
得,解得.
∴直线BC的解析式为.
∵点P的坐标为,由题意可知,
∴点E的坐标为.
∴.
∴
.
∵,
∴当时,的面积的最大值为.
②存在.
如图①,当点P在直线BC的上方,且时,则,
设直线DB的解析式为,将,点代入,
得,解得.
∴直线BD的解析式为.
∵,
∴设直线PC的解析式为.
∵,
∴.
∴.
∴直线PC的解析式为.
∴.
解得,(舍).
当时,.
∴点P的坐标为.
如图②,当点P在直线BC的下方时,设直线PC与BD交于点M,
∵,
∴.
设,
∵,
,
∴
解得.
∴点M的坐标为.
由点和点可得直线CM的解析式为,
由,
解得,(舍).
所以点.
综上,点P的坐标为或.
3.解:(1)由题可得:,,,,.
①当时,如图1,
,
,
.
,
解得:;
②当时,如图2,
同理可得:,
,
解得:;
综上所述;当为1或时,是直角三角形.
(2)分两种情况:
①当时,作于,如图3所示:
,
是等腰直角三角形,
,
的面积,
四边形的面积的面积的面积,
四边形的面积的面积,当时,面积差最小,
但是,不符合题意;
②当时,作于,如图4所示:
,
是等腰直角三角形,
,
的面积,
四边形的面积的面积的面积,
四边形的面积的面积,
当时,面积差最小;
因此,存在某一时刻,使四边形的面积与面积差最小,;
(3)根据题意得:时,存在的值,使最短,;理由如下:
如图3所示:,,
由勾股定理得:,
∴y=,
当时,y的最小值,
当时,;
当时,;
综上所述:当时,最短,最小值;
当到达时,恰好到达,此时秒,的最大值.
4.解:(1)令,则,
解得,
令,则,
所以,点,,
时,,
所以,点,
设双曲线解析式为,
则,
解得,
所以,双曲线解析式为,
点的纵坐标为,
,
解得,
点,
抛物线过点、,
,
解得,
抛物线的解析式为;
(2)当时,,
整理得,,
解得,,
点的坐标为,或,,
,
解得,
点的坐标为,
或;
(3)①点在上时,,
,
随的增大而减小,
②点在上时,,
,
时,有最大值为,
时,随的增大而减小,
③点在上时,,
,
由图可知,随的增大而减小,
综上所述,的最大值是,,,时,随的增大而减小.
5.(1)
解:联立两直线解析式可得,
解得,
点坐标为,
又点为点关于原点的对称点,
点坐标为,
直线与轴交于点,
点坐标为,
设抛物线解析式为,
把、、三点坐标代入可得,
解得,
抛物线解析式为,
故答案为:;
(2)
①当四边形为菱形时,则,
直线解析式为,
直线解析式为,
联立抛物线解析式可得,
解得或,
点坐标为,或,;
②当时,四边形的面积最大.
理由如下:
如图,过作,垂足为,作轴的垂线,交直线于点,
则,
线段长固定不变,
当最大时,四边形面积最大,
又(固定不变),
当最大时,也最大,
点在抛物线上,点在直线上,
点坐标为,点坐标为,
,
当时,有最大值1,此时有最大值,即四边形的面积最大.
6.解:(1)过点A作AD⊥x轴于D
∵等腰的斜边在x轴上,,
∴OD=DB==4,点B的坐标为(8,0)
∴AD==4
∴点A的坐标为(4,4)
由抛物线过点O,A,B,设抛物线的解析式为
将点A的坐标代入,得
解得:
∴抛物线的解析式为;
(2)①设抛物线与直线的右交点为C,
联立
解得:或
∴点C的坐标为(6,3)
当0≤m<6时,如下图所示,
∴点E的坐标为(m,),点F的坐标为(m,)
∴EF=-=
∴S矩形EFGH=FG·EF==
∵<0
∴当m=3时,S矩形EFGH有最大值,最大值为;
当6≤m≤8时,如下图所示
∴点E的坐标为(m,),点F的坐标为(m,)
∴EF=-=
∴S矩形EFGH=FG·EF==,对应抛物线的开口向上,对称轴为直线m=3,
∴在对称轴右侧,y随x的增大而增大
∵6≤m≤8
∴当m=8时,S矩形EFGH有最大值,最大值为8;
∵<8
∴矩形面积的最大值为8;
②(i)当矩形的四个顶点都在抛物线对称轴左侧时,如下图所示,此时,m+≤4,即m≤,
若矩形与等腰重叠部分为轴对称图形,易知此时四边形为正方形
∴EF=FG
∴=
解得:m1=,m2=(不符合前提,舍去)
∴此时m=;
(ii)当矩形的四个顶点中,E、F在抛物线对称轴左侧、G、H在抛物线对称轴右侧时,如下图所示,此时,m≤4且m+>4,即<m≤4,
若矩形与等腰重叠部分为轴对称图形,易知此时抛物线的对称轴直线x=4也是矩形的对称轴
∴此时点E的横坐标m=4-FG=;
(iii)当矩形的四个顶点都在抛物线对称轴右侧,且H在AB左侧时,如下图所示,矩形与等腰重叠部分为直角梯形,不可能是轴对称图形,不符合题意,舍去;
(iiii)当点H落在AB上时,设直线与AB交于点M,
∵EH∥OB
∴∠EHA=∠OBA=45°
∴矩形与等腰重叠部分为等腰直角三角形,即为轴对称图形
∴此时符合题意
设直线AB的解析式为y=kx+b
将点A、B的坐标代入,得
解得:
∴直线AB的解析式为y=-x+8
由点E(m,)
∴点H的坐标为(m+,),代入y=-x+8中,得
=-(m+)+8
解得:m=
联立
解得:
∴点M的坐标为(,)
由下图可知:从点H落在AB上到点E与点M重合之前,矩形与等腰重叠部分为等腰直角三角形,即为轴对称图形
∴此时符合题意
∴≤m<;
(iiiii)当m≥,即点E和点M重合或点E在点M右侧时,如下图所示,矩形与等腰无重叠部分,故不符合题意,舍去;
综上:m=或m=或≤m<.
7.解:(1)将A(﹣1,0),C(2,3)代入y=﹣x2+bx+c,得:
,解得:,
∴抛物线的函数关系式为y=﹣x2+2x+3.
设直线AC的函数关系式为y=kx+a(k≠0),
将A(﹣1,0),C(2,3)代入y=kx+a,得:
,解得:,
∴直线AC的函数关系式为y=x+1.
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴点D的坐标为(1,4).
当x=1时,y=x+1=2,
∴点B的坐标为(1,2).
设点E的坐标为(x,x+1).
分两种情况考虑(如图1):
①当点E在线段AC上时,点F在点E上方,
∴点F的坐标为(x,x+3).
∵点F在抛物线上,
∴x+3=﹣x2+2x+3,
解得:x1=0,x2=1(舍去),
∴点E的坐标为(0,1);
②当点E在线段AC(或CA)延长线上时,点F在点E下方,
∴点F的坐标为(x,x﹣1).
∵点F在抛物线上,
∴x﹣1=﹣x2+2x+3,
解得:,
∴点E的坐标为()或(,).
综上:满足条件的点E的坐标为(0,1),()或(,).
(3)过点P作PM⊥x轴,垂足为点M,过点C作CN⊥x轴,垂足为N,如图2所示.
设点P的坐标为(x,﹣x2+2x+3)(﹣1<x<2),则点M的坐标为(x,0).
∵点A的坐标为(﹣1,0),点C的坐标为(2,3),
∴AM=x+1,MN=2﹣x,PM=﹣x2+2x+3,CN=3,AN=3,
∴S△APC=S△APM+S梯形PMNC﹣S△ACN,
.
∴当x=时,S△APC取得最大值,最大值为,此时点P的坐标为().
8.解:(1)时,=,
当y=0时,解得x1=3,x2=-1,
∴
∴
直线MP:
∵对称轴
∴距离为.
= ,
当y1=0时,解得x1=t,x2=-t-4,
∴
∴
∴直线MP:.
对称轴:.
∵,
∴,
∴.
(2)直线MP:
对称轴:
①当,时
,
∴坐标为
②当,时
,
∴坐标为
③当,时
,
∴坐标为
综上所述:0
(3)t>4时,最高点D坐标为
P点坐标为
∴无最大值
9.(1)设抛物线的解析式为y=a(x+2)(x﹣8).
∵抛物线经过点C(0,4),
∴﹣16a=4,解得a=﹣.
∴抛物线的解析式为y=﹣(x+2)(x﹣8)=x2+x+4.
∵A(﹣2,0)、B(8,0),
∴抛物线的对称轴为x=3.
∵将x=3代入得:y=,
∴抛物线的顶点D坐标为(3,).
(2)三角形ABC是直角三角形,理由如下:
∵AB=10,AC=2,BC=4,
∴AC2+BC2=AB2.
∴∠BCA=90°,所以三角形ABC是直角三角形.
(3) ①如图1所示:作CM⊥PE,垂足为M.
设直线BC的解析式为y=kx+b.
∵将B、C的坐标代入得:,解得k=﹣,b=4,
∴直线BC的解析式为y=﹣x+4.
设点P(m,﹣ m2+m+4),则点E(m,﹣ m+4),M(m,4).
∵PC=EC,CM⊥PE,
∴PM=EM.
∴﹣m2+m+4﹣4=4﹣(﹣m+4),解得:m=0(舍去),m=4.
∴P(4,6).
②作PN⊥BC,垂足为N.
由①得:PE=﹣m2+2m.
∵PE∥y轴,PN⊥BC,
∴∠PNE=∠COB=90°,∠PEN=∠BCO.
∴△PNE∽△BOC.
∴=.
∴PN=PE=(﹣m2+2m).
由(2)知∠BCA=90°,
又∵∠PFN=∠CFA,
∴△PFN∽△CAF.
∴=﹣m2+m.
∴当m=4时,的最大值为.
10.解:(1)∵抛物线的顶点D的坐标为(1,),
∴设抛物线的解析式为y=a(x 1)2+,
将(0,0)代入,得a+=0,a= ,
∴抛物线的解析式为y= (x 1)2+,
即 y= x2+2x,
设y=0,则x=0或2,
∴点C的坐标为(0,2),
∵点P为CD的中点,
∴;
(2)在y轴右侧的抛物线上存在点Q,使以Q为圆心的圆同时与y轴、直线OP相切,
理由如下:
①若⊙Q在直线OP上方,则Q与D点重合,此时Q1(1,);
②若⊙Q在直线OP下方,与y轴、直线OP切于E、F,
则QE=QF,QE⊥y轴,QF⊥OP,
∴OQ平分∠EOF,
∵∠EOF=120°,
∴∠FOQ=60°,
∵∠POC=30°,则∠QOC=30°,
设Q(m, m),则 m= m2+2m,
解得m1=0(舍去),m2=,
∴Q2(, );
(3)证明:∵在过点O、M、D的圆中,有∠MOD=∠NOD,
∴,
∴MD=ND,
易得OD平分∠AOP,DA⊥y轴,DP⊥OP,
∴DA=DP,
可证得△NAD≌△MPD(HL),
∴MP=AN,
∴OM+ON=OP MP+OA+AN=OP+OA=2OA=,
则OM+ON=2,即OM+ON为定值;
(4)作过P、D两点且与y轴相切于点H的圆S,
则由圆周角大于圆外角可知,∠PHD最大.
设S(x,y),则由HS=SD=SP,
可得,y=2±6,
∵0<y<,
∴H(0,2 6).
11.(1)①过点作轴于,
∵△AMB为等腰直角三角形,
∴∠ABM=45°,
∵AB∥x轴,
∴∠BMN=∠ABM=45°,
∴∠MBN=90°-45°=45°,
∴∠BMN=∠MBN,
∴MN=BN,
设点坐标为,代入抛物线,得,
∴,(舍去),
∴MN=BN=1,
∴
∴
在Rt△AMB中,
∴抛物线的“完美三角形的斜边
②∵抛物线y=x2+1与y=x2的形状相同,
∴抛物线y=x2+1与y=x2的“完美三角形”的斜边长的数量关系是相等;
故答案为:相等.
(2)∵抛物线与抛物线的形状相同,
∴抛物线与抛物线的完美三角形”全等,
∵抛物线的“完美三角形”斜边的长为4,∴抛物线的“完美三角形”斜边的长为4,
∴点坐标为或,∴.
(3)∵的最大值为-1,
∴,
∴,
∵抛物线的“完美三角形”斜边长为,
抛物线的“完美三角形”斜边长为,
∴点坐标为,
∴代入抛物线,得,
∵n>0
∴,
∴,
∴
12.(1)抛物的顶点坐标为(-1,-4),伴随直线为,即,
故答案为:(-1,-4);;
(2)当时,有,
解得:,
∴点C的坐标为(-1,0),点D的坐标为(3,0).
抛物线的伴随直线为,即,
联立,
解得:,,
①∵A(1,-4m),B(2,-3m),C(-1,0),
∴,
,
.
∵∠CAB=90°,
∴,即,
解得:,(不合题意,舍去),
∴m的值为;
②过点P作PE∥y轴,交直线AC于点E,如图所示.
设直线BC的解析式为(k≠0),
将点B(2,-3m)、C(-1,0)代入,得:
,解得:,
∴直线AC的解析式为.
设点P的坐标为,则点Q的坐标为(,),
∵P是直线BC上方抛物线上的一个动点,
∴,
∴S=,
∴当时,△PBC的面积有最大值,
依题意得:,
∴.
13.(1)
解:如图,过点P作于点F,
∵点P在正方形对角线BD上,
∴∠ADP=45°,
∵,,
∴,
∴,
在Rt△中,根据勾股定理得:
,
(2)
证明:∵,,
∴
∴,
如图,作于点I,
得到矩形,矩形,
∴GI=AD,BG=CI,
∴AD=CD=GI,
∵GI=CD,∠GIC=∠CDE=90°,
∴△HIG≌△DEC(AAS),
∴HI=DE,
∴CI=CH+HI=CH+DE,
∴BG=CH+DE.
(3)
当点M在CD边上时,过点PN⊥AD于点N,
∴PNDM,
∴△EDM∽△ENP,
∴,
由(1)得:,
∴,
∴;
当点在CD延长线上时,作于点O,
由(1)知:AO=NO=2,
∵,
∴,
∵,ON=DN,,
∴△≌△(ASA),
∴,
∴,
综上:PM的长为或
(4)
点P为正方形ABCD对角线BD上的动点,
∴BD=,
∴,
∴当时,的最小值为36.
14.(1)
解:将,代入中,
可得:,
解得:,
∴抛物线的解析式为:;
(2)
解:存在,理由如下:
如图,
∵、两点关于抛物线的对称轴对称,
∴直线与的交点即为点,此时周长最小,连接、,
∵点是抛物线与轴的交点,
∴的坐标为,
又∵,
∴直线解析式为:,
∴点坐标即为,
解得:,
∴;
(3)
解:存在,理由如下:
如图,设,过点作轴交于点,连接、、,
∵,
若有最大值,则就最大,
∴,
∵,
又∵,
∴,
∴,
∴,
∴当时,最大值为.
15.(1)
∵将点A和点C的坐标代入抛物线的解析式得:,解得:.
∴抛物线的解析式为 .
∴
∴抛物线的顶点坐标为,
(2)
设直线的解析式为.
∵将点A和点C的坐标代入得,解得.
∴直线的解析式为.
如图,
设点 ,
∴,
∴ =,
∴
,
∴当m时,, ,
∴P(,);
(3)
∵落在第二象限内,H关于y轴的对称点为
∴点在第一象限,即n>0,t>0.
∵抛物线的顶点坐标为(1,4),
∴ ,
∵在抛物线上,
∴ ,
∴ ,
∵,,
∴= = = =;
∴当t时,有最小值,即有最小值,
∴ ,解得或,
∵ ,
∴不合题意,舍去,
∴n的值为.
16.(1)
解:∵抛物线与x轴交于点,
∴ ,
解得:,
∴该抛物线所对应的函数解析式为;
(2)
如图1,过点P作PQy轴交直线AF于点Q,
设直线AF的解析式为,
∵,
∴,
解得:,
∴直线AF的解析式为,
设,则Q,
∴,
∴,
∵<0,,
∴当t时,△AFP面积的最大值为;
(3)
设P(m,)(),F(0,n),
∵A(3,0),
∴OA3,OF|n|,
①当APAF,∠PAF90°时,如图2,过点P作PD⊥x轴于点D,
则∠ADP90°∠AOF,
∴∠PAD+∠APD90°,
∵∠PAD+∠FAO90°,
∴∠APD∠FAO,
在△APD和△FAO中,
,
∴△APD≌△FAO(AAS),
∴PDOA,ADOF,
∵PD,AD,OA,
∴,
解得:m0或2,
当m0时,P(0,3),AD3,
∴OF3,即|n|3,
∵点F在y的负半轴上,
∴,
∴F;
当m2时,P(2,3),AD1,
∴OF=1,即|n|1,
∵点F在y的负半轴上,
∴,
∴F(0,);
②当APPF,∠APF90°时,如图3,过点P作PD⊥x轴于点D,PG⊥y轴于点G,
则∠PDA∠PDO∠PGF90°,
∵∠PDO∠PGF∠DOG90°,
∴四边形PDOG是矩形,
∴∠FPG+∠FPD90°,
∵∠APD+∠FPD∠APF90°,
∴∠FPG∠APD,
在△FPG和△APD中,
,
∴△FPG≌△APD(AAS),
∴PGPD,FGAD,
∵PD,AD3﹣m,PGm,
∴m,
解得: (舍去), ,
当m=时,P(,),
∴=,
∴F(0,);
综上所述,点F的坐标为(0,)或(0,)或(0,).
17.(1)
解:∵∠BOC=90°,∠OBC=30°,
∴COBC,
∵BC=6,
∴CO=3,
又∵AB=3,
∴CO=AB即△ABC的边AB上的高等于AB,
∴△ABC是点A,B的“完美三角形”;
(2)
分A、B、C为直角顶点讨论:
①若C为直角顶点,如答图1,
则∠ACB=90°,作CH⊥AB于H,取AB中点M,
根据Rt△ABC是点A,B的“完美三角形”得AB=CH,
∵M为AB中点,∠ACB=90°,
∴CMAB,
CH⊥AB于H有CM≥CH,
∴AB≥AB得AB≤0,这和AB为线段矛盾,
故C不可能为直角顶点;
②若A为直角顶点,如答图2,过A作y轴平行线交直线y=2x﹣5于C,
∵A(4,0),
∴C点横坐标=4,代入y=2x﹣5得C纵坐标=3,即AC=3,
∵Rt△ABC是点A,B的“完美三角形”,
∴AB=3,
∴(1,0)或(7,0);
③若B为直角顶点,如答图3,过B作y轴平行线交直线y=2x﹣5于C,
设B(m,0),则C(m,2m﹣5),
∴BC=|2m﹣5|,
而A(4,0),故AB=|4﹣m|,
∵Rt△ABC是点A,B的“完美三角形”,
∴BC=AB,即|2m﹣5|=|4﹣m|,
由2m﹣5=4﹣m得m=3,此时(3,0),
由2m﹣5=m﹣4得m=1,此时(1,0);
综上所述,Rt△ABC是点A,B的“完美三角形”,(1,0)或(7,0)或(3,0);
(3)
由得,,
如答图4,
∴R(﹣1,1),S(2,4),
∴RS=3,
∵△RSN为点R,S的“完美三角形”,
∴N到RS的距离为3,
令y=x+2中y=0可得x=﹣2,即直线y=x+2与x轴交点D(﹣2,0),
过D作DE⊥RS,在垂线上取DE=3,(注:点M是线段RS下方抛物线上的一个动点,且M,N两点之间距离的最小值,故E应在D右侧)
∵直线y=x+2与x轴夹角∠ODR=45°,
∴∠ODE=45°,
过E作EFRS交x轴于F,则△DEF是等腰直角三角形,
∵DE=3,
∴DF=6,
∴F(4,0),
设EF解析式为y=x+b,将F(4,0)代入可得EF为y=x﹣4,
即N点在直线y=x﹣4上,且直线y=x﹣4与y轴交点P(0,﹣4)
∵线段RS下方抛物线上的一个动点M到EF距离最近,
∴将直线y=x﹣4平移至与抛物线只有一个交点时,此交点即为M,
设此时直线为y=x+c,
由联立方程只有一个交点,
得,即,
可得c,即直线MN为y=x,
∴直线MN与y轴交点G(0,),过G作GH⊥EF于H,则△GHP是等腰直角三角形,且GP,
∴GH,
∴M,N两点之间距离的最小值是,
故答案为:.
18.(1)
解:∵,
令x=0,则y=3,
令y=0,则,
解得x=-4或1,
∴A(-4,0),B(1,0),C(0,3),
∵,
∴对称轴为直线x=-;
(2)
解:如图所示:
过N作NQ⊥x轴于点Q,
由旋转性质得MB⊥x轴,∠CBN=90°,BM=AB=5,BN=BC,
∴M(1,5),∠OBC+∠QBN=90°,
∵∠OBC+∠BCO=90°,
∴∠BCO=∠QBN,
又∵∠BOC=∠NQB=90°,BN=BC,
∴△OBC≌△QNB(AAS),
∴BQ=OC=3,NQ=OB=1,
∴OQ=1+3=4,
∴N(4,1);
(3)
解:设直线NB的解析式为y=kx+b.
∵B(1,0)、N(4,1)在直线NB上,
∴,
解得:,
∴直线NB的解析式为:y=x-,
当点P,N,B在同一直线上时|NP-BP|=NB=,
当点P,N,B不在同一条直线上时|NP-BP|<NB,
∴当P,N,B在同一直线上时,|NP-BP|的值最大,
即点P为直线NB与抛物线的交点.
解方程组:,
解得:或,
∴当P的坐标为(1,0)或时,|NP-BP|的值最大,此时最大值为.
19.(1)
解:证明:如图1,
四边形是正方形,
,,,
,,
,
,
,
,
,
,
.
(2)
,
证明:如图2,连接,作交于点,
,,
,,
,,
,
,
,
,
,,
,
,
,
,
,
,
,
.
(3)
如图3,设,,
,
,
,
,
,
,
,
,
,
当时,,
当,达到最大值,最大值是,
故答案为:1,.
20.(1)
解:将点A(1,0)、B( 3,0)代入y=,
得:,
解得:
∴二次函数解析式为.
(2)
①令x=0,代入,得:,
∴C(0,3),
∵B(-3,0),
∴设直线BC的解析式为y=kx+b,代入得
,
解得:,
∴直线BC的解析式为:y=x+3
设F(x,),则E(x,x+3)
∴FE=-(x+3)=,
∴的面积=()=,
∴x=-时,的面积最大,此时F(-,);
②Ⅰ当∠CFE=90°时,如图:
∵DFy轴,
∴DF⊥x轴,
∴∠ODF=∠CFE=90°,
∴CFOB,
∴点F的纵坐标为3,
∴3=﹣﹣2x+3,
解得=0(舍去),=﹣2,
∴F(﹣2,3),
Ⅱ当∠ECF=90°时,过点C作CH⊥EF于H,
∵DFy轴,
∴DF⊥x轴,
∴∠BDE=90°,
∵C(0,3),B(﹣3,0),
∴OC=OB=3,
∴∠OBC=45°,
∴∠OEB=∠CEH=45°,
∵∠ECF=90°,
∴CE=CF,
∵CH⊥EF,
∴EF=2CH,
设D(m,0),则E(m,m+3),F(m,),
∴EF=﹣(m+3)=﹣﹣3m,CH=﹣m,
∴﹣﹣3m=﹣m,
∴=0(舍去),=﹣1,
∴点D坐标为(﹣1,0).
∴F(﹣1,4)
综上,点F的坐标为(﹣2,3)或(﹣1,4).
21.(1)
∵抛物线的顶点为A,
∴.A的横坐标为2,
又∵直线AB的解析式为
∴当时,,当时,
∴点A的坐标为(2,4),B(,0)
将(2,4),(,0)代入得:,
∴抛物线的解析式为.
(2)
由(1)得:
∵对称轴为直线,B(,0)
设E(t,),N(t,)
∴当时,EN最大为1
∴E(4,3)
∵AD是此抛物线的对称轴
∴过点E作AD的对称点(0,3),连接交AD于点P,此时最短,M(5,)
(3)
如图①所示:
设GF交x轴于点E,在中,,,
∴,
∴,
将代入抛物线的解析式可得:,
∴点F的坐标为(3,)
在与中,
∴,
又∵点A的坐标为(2,4)
∴H的坐标为(1,3);
同理如图②所示,
在中,,,
∴,
∴,
将代入抛物线的解析式可得:,
∴F的坐标为(7,),
在与中,
∴,
又∵点A的坐标为(2,4)
∴H的坐标为(3,5);
综上所述,H(1,3),点F(3,)或H(3,5),F(7,).
22.(1)
解:当时,;
当时,,;
,,
点,在抛物线上,
,解得:,
;
(2)
当以AC为边时,点N的坐标为(,);当以AC为对角线时,点N的坐标为(,);
∵抛物先线的函数表达式:,
∴抛物线的对称轴为:x=,
当y=0时,,解得:x=-3或x=4,
∴点A(-3,0),
设点N(,n),点M(m,),
①当AN为平行四边形的边时,AM和CN为对角线,
,解得:,
∴N(,)
②当AM为平行四边形的边时,AN和CM为对角线,
,解得:
∴N(,),
综上:点N的坐标为:(,)或(,).
(3)
如图1,连接,延长交轴于,
轴,
轴,
设,,
,
,且,,,
,
,
,
∵,
∴,
当时,有最大值是,
23.(1)
解:∵OB=3OA,
∴设A(-β,0),则B(3β,0),
∵对称轴是x=1,
∴=1,
∴β=1,
∴A(-1,0),B(3,0),
∴,解得:,
∴抛物线的表达式为,
当x=1时,y=1-2-3=-4,
∴点D的坐标为(1,4);
(2)
解:∵A(-1,0),B(3,0),D (1,4),
设直线AD的表达式为y=kx+c,
∴,解得,
∴直线AD的表达式为y=-2x-2,
当x=0时,y=-2,
∴点E的坐标为(0,-2),
∵P是抛物线上的一个动点,Q是抛物线对称轴上一个点,
∴设P(m,),Q(1,t),
①当BE为边时,PQBE且PQ=BE,
当E对应Q,由(0,-2)变为(1,t),要向右平移1个单位,
则当B(3,0)对应P(m,),也要向右平移1个单位,即m=3+1=4,
∴=5,
∴P(4,5);
当E对应P,B对应Q,由(3,0)变为(1,t),向左平移2个单位,
则由(0,-2)变为(m,),也向左平移2个单位,
∴m=0-2=-2,
∴m2-2m-3=5,
∴P(-2,5);
②当BE为对角线时,BE的中点坐标为(,),即(,),
∴PQ的中点坐标也为(,),
∴=,∴m=2,则=-3,
∴P(2,-3);
综上,点P的坐标为(4,5)或(-2,5)或(2,-3);
(3)
解:∵点P在第四象限的抛物线上,AP、BE交于点G,
设P(m,),其中0<m<3,
设直线AP的表达式为y=cx+d,
∵A(-1,0),P(m,),
∴,解得:,
∴直线AP的表达式为y=(m-3)x+m-3,
同理求得直线BE的表达式为y=x-2,
联立方程组,得:,
解得:,
∴,
∵0<m<3,
∴24-8m>0,3m-11<0,
∴,
∴
令,
∵-3<0,
∴当m=时,z取得最大值,w取得最小值为,
∴w有最小值,最小值为.
(4)
解:当x=0时,y=-3,
∴点C的坐标为(0,-3),
∵点B的坐标为(3,0),
∴OB=3,OC=3,
∴△OBC是等腰直角三角形,
∴∠OBC=∠OCB=45°,
同理求得直线BC的表达式为y=x-3,
∵点C和M关于抛物线对称轴对称,
∴点M的坐标为(2,-3),
过点N作NH⊥x轴于点H,
∵∠OBC=45°,
∴△BHN是等腰直角三角形,
∴HN=BN,
∴,
∴当M、N、H在同一直线上时,取得最小值,
∴的最小值为3.
故答案为:3.
