九年级数学下册试题 1.5 三角函数在相似三角形中的应用-北师大版(含答案)
文档属性
| 名称 | 九年级数学下册试题 1.5 三角函数在相似三角形中的应用-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 08:55:59 | ||
图片预览




文档简介
1.5 三角函数在相似三角形中的应用
第一课时
1.如图,在中,,于点,交边于点,过点作的垂线交的延长线于点.
(1)求证:;
(2)当,,求的长
2.如图,已知在中,,垂足为点 , 点是边的中点.
(1)求边的长;
(2)求的正弦值.
3.如图,△ABC中,∠ACB=90°,CD⊥AB于点D,E是AC的中点,DE的延长线交BC的延长线于点F,EF=5,∠B的正切值为
(1)求证:△BDF∽△DCF;
(2)求BC的长.
4.已知:如图,在△ABC中,AB=AC=6,BC=4,AB的垂直平分线交AB于点E,交BC的延长线于点D.
(1)求CD的长;
(2)求点C到ED的距离.
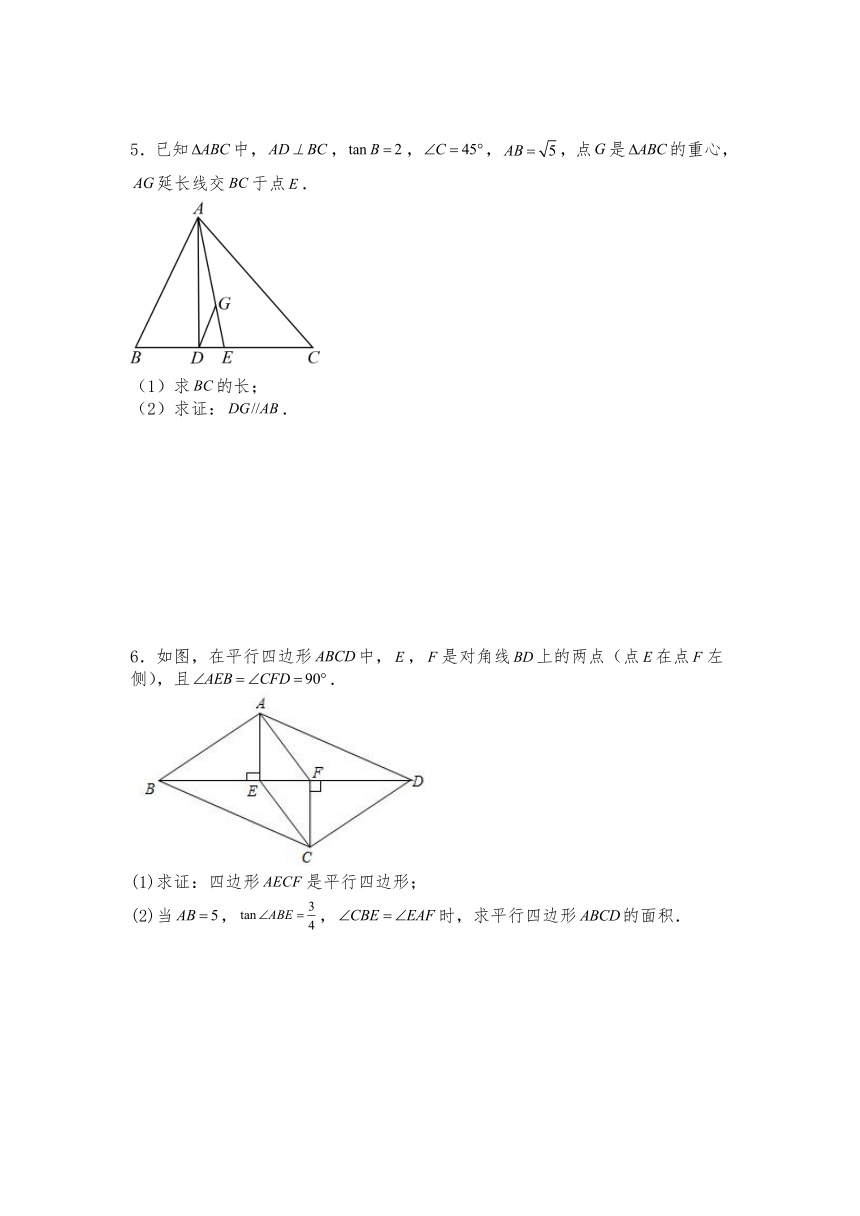
5.已知中,,,,,点是的重心,延长线交于点.
(1)求的长;
(2)求证:.
6.如图,在平行四边形中,,是对角线上的两点(点在点左侧),且.
(1)求证:四边形是平行四边形;
(2)当,,时,求平行四边形的面积.
7.如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
(1)求证:;
(2)若,S△AOD=4,求S△BOC的值.
8.如图,已知点D、E分别在△ABC中的边BA、CA的延长线上,且DEBC.
(1)如果AD=3,BD=9,DE=4,求BC的长;
(2)如果,AD=4,sinB,过点D作BF⊥BC,垂足为点F,求DF的长.
9.如图,已知点、分别在中的边、的延长线上,且.
(1)如果,,,求的长;
(2)如果,,,过点作,垂足为点,求的长.
10.如图,在和中,,,AC与DE相交于点F,联结CE,点D在边BC上.
(1)求证:∽;
(2)若,求的值.
11.如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(﹣3,4),AB⊥x轴于点E,正比例函数y=ax的图象与反比例函数y=的图象相交于A,P两点.
(1)求a,b的值与点A的坐标;
(2)求证:△CPD∽△AEO;
(3)求sin∠CDB的值.
12.如图,在梯形ABCD中,,,,对角线AC与BD交于点E.点F是线段EC上一点,且.
(1)求证:;
(2)如果,,求FC的长.
第二课时
1.矩形ABCD中,AB=2,AD=4,F是对角线AC上不与点A,C重合的一点,过F作FE⊥AD于E,将△AEF沿EF翻折得到△GEF,点G在线段AD上,连接CG,∠FGC=90°,延长GF交AB于H,连接CH.
(1)求证:△CDG∽△GAH;
(2)求tan∠GHC.
2.如图,在四边形中,,于点,点是延长线上一点,,于点.
(1)求证:四边形是菱形;
(2)若平分,,,求和的长.
3.如图,菱形ABCD中,,,E为AB边上一点,作,其两边分别交菱形的边于点F,G.
(1)如图1,点E与点A重合,点F,G分别在边BC,CD上,求证:;
(2)如图2,.当,点F在边BC上时,求BF的长;
(3)如图3,E为AB的中点.当时,请直接写出EG的长.
4.如图,在边长为6的正方形ABCD中,Q在CD的延长线上,H在CB的延长线上,∠HCQ绕点C逆时针旋转,得到,交AB于点E,交AD的延长线于点N,交BD于点F,NE与BD的交点为M,连结CM.当时.
(1)求ND的长.
(2)求证:
(3)求CM的长.
5.问题背景:
一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图1,已知AD是△ABC的角平分线,可证=.小慧的证明思路是:如图2,过点C作CE∥AB,交AD的延长线于点E,构造相似三角形来证明=.
(1)尝试证明:请参照小慧提供的思路,利用图2证明=;
(2)应用拓展:如图3,在Rt△ABC中,∠BAC=90°,D是边BC上一点.连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB上的E点处.
①若AC=1,AB=2,求DE的长;
②若BC=m,∠AED=,求DE的长(用含m,的式子表示).
6.如图,在矩形ABCD中,点E在边AD上,,的平分线BF交CE于点G,交CD于点F.
(1)如图1,若点E为AD中点,求证:;
(2)如图2,若,求证:;
(3)如图3,若,DF=4,求的值.
7.已知,在中,,,.点P、H分别是边BC、AB上一点,将沿PH翻折,使得点B落在AB边上的点D处.
(1)如图1,PE平分,交AC边于点E,连接DE.
①探索PE与AB位置关系,证明你的结论;
②若,求的面积;
(2)连接CD,若,求BP的长.
8.在中,,点D是的中点,点P是上一动点(不与点C,D重合),过点C作交射线于点E,过点D作交于点F.
(1)观察猜想
如图(1).当时,_______,线段之间的数量关系为________.
(2)类比探究
当时,如图(2),求的度数,并探究线段之间的数量关系.
(3)解决问题
当时,若,点P是边上一动点(不与点B,C,D重合),其他条件不变,当点A,F,E中的一点是另外两点的连线的中点时,直接写出的长.
第一课时答案
1.(1)
∵AB=AC,
∴∠ABC=∠ACB,
∵∠AEC=90°+∠ABC,∠ACD=90°+∠ACB,
∴∠AEC=∠ACD,
∵∠EAC=∠CAD,
∴△AEC∽△ACD.
(2)
∵∠BAE=∠DCE=90°,∠BEA=∠DEC
∴∠ABE=∠CDE,
∴tan∠B=tan∠D=,
设AE=x,则AB=AC=2x,
∵△AEC∽△ACD,
∴,
∴AD=4x,
∴ED=AD-AE=3x,
∵CE=1,CD=2,
∴ED=,
∴3x=,
∴4x=,
即AD=.
2.
(1)
∵
∴和均为直角三角形,
∵
∴
∵
∴
∵
由勾股定理得,
(2)
过点作于点F,如图,
∵,
∴//
∴
∴
∵点是边的中点
∴
∴
∵
∴
∴
∴
在中,∵
∴
∴
3.(1)
证明:∵CD⊥AB,
∴∠ADC=90°,
∵E是AC的中点,
∴DE=EC,
∴∠EDC=∠ECD,
∵∠ACB=90°,∠BDC=90°
∴∠ECD+∠DCB=90°,∠DCB+∠B=90°,
∴∠ECD=∠B,
∴∠B=∠FDC,
又∵∠F=∠F,
∴△BDF∽△DCF;
(2)
解:设DE=x,则AC=2DE=2x,DF=DE+EF=x+5.
∵△BDF∽△DCF,
∴===tan∠B=,
∴BF=2DF=2(x+5),CF=DF=(x+5),
∴BC=BF﹣CF=(x+5),
在直角△ABC中,∵tan∠B==,
∴BC=2AC,即(x+5)=2×2x,
解得x=3
∴BC=(3+5)=12.
4.解:(1)过A点作AF⊥BC于点F.
∵AB=AC=6,BC=4,AF⊥BC,
∴BF=FC=2,∠BFA=90°.
∴在Rt△ABF中,.
∵DE垂直平分AB,AB=6,
∴AE=BE=3,∠DEB=90°.
在Rt△DEB中,,
∴BD=9,
∴CD=BD-BC=5.
(2)过C点作CH⊥ED于点H.
∵CH⊥ED,AB⊥ED,
∴∠DEB=∠DHC=90°,
∴CH∥AB,
∴.
∵BE=3,BD=9,CD=5,
∴,
∴点C到ED的距离CH为.
5.(1)解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,∵tanB==2,
∴AD=2BD,
∵BD2+AD2=AB2,
∴BD2+4BD2=()2,解得BD=1,
∴AD=2,
在Rt△ADC中,∵∠C=45°,
∴CD=AD=2,
∴BC=BD+CD=1+2=3;
(2)解:∵点G是△ABC的重心,
∴AG=2GE,BE=CE=BC=,
∴DE=BE BD= 1=,
∵,,
∴,
而∠DEG=∠BEA,
∴△EDG∽△EBA,
∴∠EDG=∠B,
∴DG∥AB.
6.(1)
证明:∵四边形ABCD是平行四边形,
∴AB=CD,,
∴;
∵,
∴
∴,
在△ABE和△CDF中:
∴△ABE≌△CDF
∴AE=CF
又,
∴四边形是平行四边形;
(2)
解:∵在Rt△ABE中,,
∴,
设AE=3x,则BE=4x,
∴,即:,
解得(-1舍去),
∴AE=3x=3,BE=4x=4,
由(1)可知,四边形是平行四边形,
∴CF=AE=3,
∵,∠AEF=∠CFB=90°,
∴△AEF∽△BFC
∴,即,
解得:,或(舍去),
∴,
∴平行四边形的面积:.
7.(1)证明: AB⊥AC,CD⊥BD,
,
,
,
,
,
又,
;
(2)解:在 中,,
,
,
,
S△AOD=4,
.
8.(1)
∵,
∴,
∵,
∴
∵,
∴
∴
(2)
∵,
∴,
∵
∴,
∵,
∴,
∴
∵,垂足为点,
∴,
在中,,
即,
∴
9.(1)
解:∵,
∴∠E=∠C,∠EDA=∠B,
∴△DEA∽△BCA,
∴,
∵,,
∴,
∵,
∴.
∴.
(2)
解:∵,
∴△DEA∽△BCA,
∴,
∵,
∴,
∵,
∴,
∴,
∵,垂足为点,
∴.
在中,,
即,
∴.
10.(1)∵,,
∴∽,
∴,
∵,
∴,
∴∽.
(2)∵∽,
∴,即,
在中,,
∴
∴,
∵∽.
∴,
∵
∴∽,
∴.
11.(1)
解:将点P(﹣3,4)代入y=ax,得:4=﹣3a,
解得:a=﹣,
∴正比例函数解析式为y=﹣x;
将点P(﹣3,4)代入y=,得:﹣12=b﹣3,
解得:b=﹣9,
∴反比例函数解析式为y=﹣.
∵正比例函数与反比例函数都关于原点对称,
∴点A的坐标为(3,﹣4).
(2)
证明:∵四边形ABCD是菱形,
∴AC⊥BD,ABCD,
∴∠DCP=∠BAP,即∠DCP=∠OAE.
∵AB⊥x轴,
∴∠AEO=∠CPD=90°,
∴△CPD△AEO.
(3)
解:∵点A的坐标为(3,﹣4),
∴AE=4,OE=3,.
∵△CPD∽△AEO,
∴∠CDP=∠AOE,
∴sin∠CDB=sin∠AOE=.
12.(1)
证明:∵ ,
∴△EAD∽△ECB,
∴ ,即,
∵,∠AEB=∠DEF,
∴△ABE∽△DFE,
∴ ,
∴,
∴;
(2)
解:∵, ,,
∴ ,即AC=9,
∴ ,
∵,
∴AD=3,
∵,
∴∠BAD=90°,
∴ ,
∵△EAD∽△ECB,
∴ ,
∴ , ,
∴ ,,
∴EC=6, ,
∵,
∴ ,
∴EF=4,
∴FC=EC-EF=6-4=2.
第二课时答案
1.(1)
证明:∵四边形ABCD是矩形,
∴∠D=∠GAH=90°,
∴∠DCG+∠DGC=90°,
∵∠FGC=90°,
∴∠AGH+∠DGC=90°,
∴∠DCG=∠AGH,
∴△CDG∽△GAH;
(2)
解:由翻折得∠EGF=∠EAF,
∴∠AGH=∠DAC=∠DCG,
∵CD=AB=2,AD=4,
∴,
∴DG=CD=×2=1,
∴GA=4-1=3,
∵△CDG∽△GAH,
∴,
∴tan∠GHC=.
2.(1)
证明:∵,,
∴,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是菱形.
(2)
解:∵四边形是菱形,
∴,平分,,
∵平分,,
∴,和都是直角三角形,
∵,,
∴在中,,,
∴,
∴,
∴,
在中,,,
∴,
∴,
∴,
∴.
∴的长为,的长为.
3.(1)
证明:连接AC,如图,
∵四边形ABCD为菱形,
∴,.
∴,为等边三角形.
∴,.
又∵,∴.
∴.
∴.
(2)
解:连接AC,由题意可得:,
①如图,
当G在BC上时,作,交AB于点H.
∴,
∴为等边三角形.
.而
∴,,
∴.
∴.
∵,,,
∴.
②如图,
当G在CD上时,作,交BA的延长线于点H.
∵四边形ABCD为菱形,
∴.
∴四边形ACGH是平行四边形.
∴,
∴.
∵,
∴.
∴.
∴.
∴.
∴.
∵,,,
∴.
综上所述:或.
(3)
分三种情况:
第一种,如图,当G与A重合时,过作于F,连接EF,
为的中点,
四边形为平行四边形,
,
所以此时
第二种,①如图,当F与A重合,且时,
同理:四边形是平行四边形,
;
②如图,
结合①把沿折叠,则
此时
结合菱形的性质可得:落在BC上,
此时
第三种,如图,当在上,
过作,
而而为两平行线间的距离,则也为两平行线间的距离,
过作于
则
为等边三角形,
综上:的长为2,4或.
4.(1)
解:(1)由题意可知,
∵,
∴.
∵,,
∴,
∴.
(2)
证明:∵,
∴,
∵,
∴.
∵,
∴.
∵,
∴,
∴,
∴.
(3)
解:∵,
∴.
∵,
∴,
∴.
∵,
∴△MCE为等腰直角三角形,
.
在Rt△BEC中,,
∴.
5.(1)
解:∵AB∥CE,
∴∠BAD=∠DEC,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠CAD=∠DEC,
∴AC=EC,
∵∠BDA=∠CDE,
∴,
∴,
即,
∴;
(2)
①由折叠可知,AD平分∠BAC,CD=DE,
由(1)得,,
∵AC=1,AB=2,
∴,
∴,
解得:CD=,
∴DE= CD=;
②由折叠可知∠AED=∠C=,
∴,
由①可知,
∴,
∴,
即:.
6.(1)
解:在矩形中,,AD∥BC
∵点为中点,
∴,
在和中,
,
∴;
∴∠AEB=∠DEC,
∵,
∴∠AEB+∠DEC=2∠AEB=180°-∠BEC=90°,
∴∠AEB=45°,
∵AD∥BC,
∴∠EBC=AEB=45°;
(2)
证明:在矩形中,,
∴∠AEB=∠EBC,
∵∠BEC=∠A=90°,
∴△ABE∽△ECB,
∴,
∵,
∴,
∵平分,
∴∠EBG=∠CBF,
∵,
∴△BEG∽△BCF,
∴,
∴,
∴;
(3)
解:过点F作FH⊥BE,交BE延长线于H,连接,如图,
∵,FH⊥BE,
∴,
∴,
∵平分,
∴∠HBF=∠CBF,
在△BHF和△BCF中,
,
∴△BHF≌△BCF(AAS),
∴BH=BC,,HF=CF,
∴,
∴,
在△BHG和△BCG中,
,
∴△BHG≌△BCG(SAS),
∴HG=CG,
∴四边形为菱形,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴.
7.(1)
①.
证明:∵PE平分,
∴,
∴,
又∵,
∴,
∴.
②∵,
∴,
∵,
∴,,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,,
∴由勾股定理得,
∴,
∴,,
将沿PH翻折,使得点B落在AB边上的点D处,
,
,
∴.
(2)
如图,
取AB的中点F,连接CF,
,
∴,,
∴,
∵,
∴,
∴,
∴,
,
,
,
∴,
∴,
∴,
∴.
8.(1)
连接AD,
,点D是的中点,
,,
,
,
,即,
,
,
,
在和中,又,
,
,
,
,
,
故答案为:45°,;
(2)
连接AD,
,点D是的中点,
,
,
,
,
,
,
,
,
,
;
(3)
当点F是AE的中点时,如图
,
在中,根据勾股定理得,
即,
,
,
;
当点E是AF的中点时,如图,连接AD,
,
,
在中,根据勾股定理得,
即,
,
,
;
综上,的长为或.
第一课时
1.如图,在中,,于点,交边于点,过点作的垂线交的延长线于点.
(1)求证:;
(2)当,,求的长
2.如图,已知在中,,垂足为点 , 点是边的中点.
(1)求边的长;
(2)求的正弦值.
3.如图,△ABC中,∠ACB=90°,CD⊥AB于点D,E是AC的中点,DE的延长线交BC的延长线于点F,EF=5,∠B的正切值为
(1)求证:△BDF∽△DCF;
(2)求BC的长.
4.已知:如图,在△ABC中,AB=AC=6,BC=4,AB的垂直平分线交AB于点E,交BC的延长线于点D.
(1)求CD的长;
(2)求点C到ED的距离.
5.已知中,,,,,点是的重心,延长线交于点.
(1)求的长;
(2)求证:.
6.如图,在平行四边形中,,是对角线上的两点(点在点左侧),且.
(1)求证:四边形是平行四边形;
(2)当,,时,求平行四边形的面积.
7.如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
(1)求证:;
(2)若,S△AOD=4,求S△BOC的值.
8.如图,已知点D、E分别在△ABC中的边BA、CA的延长线上,且DEBC.
(1)如果AD=3,BD=9,DE=4,求BC的长;
(2)如果,AD=4,sinB,过点D作BF⊥BC,垂足为点F,求DF的长.
9.如图,已知点、分别在中的边、的延长线上,且.
(1)如果,,,求的长;
(2)如果,,,过点作,垂足为点,求的长.
10.如图,在和中,,,AC与DE相交于点F,联结CE,点D在边BC上.
(1)求证:∽;
(2)若,求的值.
11.如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(﹣3,4),AB⊥x轴于点E,正比例函数y=ax的图象与反比例函数y=的图象相交于A,P两点.
(1)求a,b的值与点A的坐标;
(2)求证:△CPD∽△AEO;
(3)求sin∠CDB的值.
12.如图,在梯形ABCD中,,,,对角线AC与BD交于点E.点F是线段EC上一点,且.
(1)求证:;
(2)如果,,求FC的长.
第二课时
1.矩形ABCD中,AB=2,AD=4,F是对角线AC上不与点A,C重合的一点,过F作FE⊥AD于E,将△AEF沿EF翻折得到△GEF,点G在线段AD上,连接CG,∠FGC=90°,延长GF交AB于H,连接CH.
(1)求证:△CDG∽△GAH;
(2)求tan∠GHC.
2.如图,在四边形中,,于点,点是延长线上一点,,于点.
(1)求证:四边形是菱形;
(2)若平分,,,求和的长.
3.如图,菱形ABCD中,,,E为AB边上一点,作,其两边分别交菱形的边于点F,G.
(1)如图1,点E与点A重合,点F,G分别在边BC,CD上,求证:;
(2)如图2,.当,点F在边BC上时,求BF的长;
(3)如图3,E为AB的中点.当时,请直接写出EG的长.
4.如图,在边长为6的正方形ABCD中,Q在CD的延长线上,H在CB的延长线上,∠HCQ绕点C逆时针旋转,得到,交AB于点E,交AD的延长线于点N,交BD于点F,NE与BD的交点为M,连结CM.当时.
(1)求ND的长.
(2)求证:
(3)求CM的长.
5.问题背景:
一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图1,已知AD是△ABC的角平分线,可证=.小慧的证明思路是:如图2,过点C作CE∥AB,交AD的延长线于点E,构造相似三角形来证明=.
(1)尝试证明:请参照小慧提供的思路,利用图2证明=;
(2)应用拓展:如图3,在Rt△ABC中,∠BAC=90°,D是边BC上一点.连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB上的E点处.
①若AC=1,AB=2,求DE的长;
②若BC=m,∠AED=,求DE的长(用含m,的式子表示).
6.如图,在矩形ABCD中,点E在边AD上,,的平分线BF交CE于点G,交CD于点F.
(1)如图1,若点E为AD中点,求证:;
(2)如图2,若,求证:;
(3)如图3,若,DF=4,求的值.
7.已知,在中,,,.点P、H分别是边BC、AB上一点,将沿PH翻折,使得点B落在AB边上的点D处.
(1)如图1,PE平分,交AC边于点E,连接DE.
①探索PE与AB位置关系,证明你的结论;
②若,求的面积;
(2)连接CD,若,求BP的长.
8.在中,,点D是的中点,点P是上一动点(不与点C,D重合),过点C作交射线于点E,过点D作交于点F.
(1)观察猜想
如图(1).当时,_______,线段之间的数量关系为________.
(2)类比探究
当时,如图(2),求的度数,并探究线段之间的数量关系.
(3)解决问题
当时,若,点P是边上一动点(不与点B,C,D重合),其他条件不变,当点A,F,E中的一点是另外两点的连线的中点时,直接写出的长.
第一课时答案
1.(1)
∵AB=AC,
∴∠ABC=∠ACB,
∵∠AEC=90°+∠ABC,∠ACD=90°+∠ACB,
∴∠AEC=∠ACD,
∵∠EAC=∠CAD,
∴△AEC∽△ACD.
(2)
∵∠BAE=∠DCE=90°,∠BEA=∠DEC
∴∠ABE=∠CDE,
∴tan∠B=tan∠D=,
设AE=x,则AB=AC=2x,
∵△AEC∽△ACD,
∴,
∴AD=4x,
∴ED=AD-AE=3x,
∵CE=1,CD=2,
∴ED=,
∴3x=,
∴4x=,
即AD=.
2.
(1)
∵
∴和均为直角三角形,
∵
∴
∵
∴
∵
由勾股定理得,
(2)
过点作于点F,如图,
∵,
∴//
∴
∴
∵点是边的中点
∴
∴
∵
∴
∴
∴
在中,∵
∴
∴
3.(1)
证明:∵CD⊥AB,
∴∠ADC=90°,
∵E是AC的中点,
∴DE=EC,
∴∠EDC=∠ECD,
∵∠ACB=90°,∠BDC=90°
∴∠ECD+∠DCB=90°,∠DCB+∠B=90°,
∴∠ECD=∠B,
∴∠B=∠FDC,
又∵∠F=∠F,
∴△BDF∽△DCF;
(2)
解:设DE=x,则AC=2DE=2x,DF=DE+EF=x+5.
∵△BDF∽△DCF,
∴===tan∠B=,
∴BF=2DF=2(x+5),CF=DF=(x+5),
∴BC=BF﹣CF=(x+5),
在直角△ABC中,∵tan∠B==,
∴BC=2AC,即(x+5)=2×2x,
解得x=3
∴BC=(3+5)=12.
4.解:(1)过A点作AF⊥BC于点F.
∵AB=AC=6,BC=4,AF⊥BC,
∴BF=FC=2,∠BFA=90°.
∴在Rt△ABF中,.
∵DE垂直平分AB,AB=6,
∴AE=BE=3,∠DEB=90°.
在Rt△DEB中,,
∴BD=9,
∴CD=BD-BC=5.
(2)过C点作CH⊥ED于点H.
∵CH⊥ED,AB⊥ED,
∴∠DEB=∠DHC=90°,
∴CH∥AB,
∴.
∵BE=3,BD=9,CD=5,
∴,
∴点C到ED的距离CH为.
5.(1)解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,∵tanB==2,
∴AD=2BD,
∵BD2+AD2=AB2,
∴BD2+4BD2=()2,解得BD=1,
∴AD=2,
在Rt△ADC中,∵∠C=45°,
∴CD=AD=2,
∴BC=BD+CD=1+2=3;
(2)解:∵点G是△ABC的重心,
∴AG=2GE,BE=CE=BC=,
∴DE=BE BD= 1=,
∵,,
∴,
而∠DEG=∠BEA,
∴△EDG∽△EBA,
∴∠EDG=∠B,
∴DG∥AB.
6.(1)
证明:∵四边形ABCD是平行四边形,
∴AB=CD,,
∴;
∵,
∴
∴,
在△ABE和△CDF中:
∴△ABE≌△CDF
∴AE=CF
又,
∴四边形是平行四边形;
(2)
解:∵在Rt△ABE中,,
∴,
设AE=3x,则BE=4x,
∴,即:,
解得(-1舍去),
∴AE=3x=3,BE=4x=4,
由(1)可知,四边形是平行四边形,
∴CF=AE=3,
∵,∠AEF=∠CFB=90°,
∴△AEF∽△BFC
∴,即,
解得:,或(舍去),
∴,
∴平行四边形的面积:.
7.(1)证明: AB⊥AC,CD⊥BD,
,
,
,
,
,
又,
;
(2)解:在 中,,
,
,
,
S△AOD=4,
.
8.(1)
∵,
∴,
∵,
∴
∵,
∴
∴
(2)
∵,
∴,
∵
∴,
∵,
∴,
∴
∵,垂足为点,
∴,
在中,,
即,
∴
9.(1)
解:∵,
∴∠E=∠C,∠EDA=∠B,
∴△DEA∽△BCA,
∴,
∵,,
∴,
∵,
∴.
∴.
(2)
解:∵,
∴△DEA∽△BCA,
∴,
∵,
∴,
∵,
∴,
∴,
∵,垂足为点,
∴.
在中,,
即,
∴.
10.(1)∵,,
∴∽,
∴,
∵,
∴,
∴∽.
(2)∵∽,
∴,即,
在中,,
∴
∴,
∵∽.
∴,
∵
∴∽,
∴.
11.(1)
解:将点P(﹣3,4)代入y=ax,得:4=﹣3a,
解得:a=﹣,
∴正比例函数解析式为y=﹣x;
将点P(﹣3,4)代入y=,得:﹣12=b﹣3,
解得:b=﹣9,
∴反比例函数解析式为y=﹣.
∵正比例函数与反比例函数都关于原点对称,
∴点A的坐标为(3,﹣4).
(2)
证明:∵四边形ABCD是菱形,
∴AC⊥BD,ABCD,
∴∠DCP=∠BAP,即∠DCP=∠OAE.
∵AB⊥x轴,
∴∠AEO=∠CPD=90°,
∴△CPD△AEO.
(3)
解:∵点A的坐标为(3,﹣4),
∴AE=4,OE=3,.
∵△CPD∽△AEO,
∴∠CDP=∠AOE,
∴sin∠CDB=sin∠AOE=.
12.(1)
证明:∵ ,
∴△EAD∽△ECB,
∴ ,即,
∵,∠AEB=∠DEF,
∴△ABE∽△DFE,
∴ ,
∴,
∴;
(2)
解:∵, ,,
∴ ,即AC=9,
∴ ,
∵,
∴AD=3,
∵,
∴∠BAD=90°,
∴ ,
∵△EAD∽△ECB,
∴ ,
∴ , ,
∴ ,,
∴EC=6, ,
∵,
∴ ,
∴EF=4,
∴FC=EC-EF=6-4=2.
第二课时答案
1.(1)
证明:∵四边形ABCD是矩形,
∴∠D=∠GAH=90°,
∴∠DCG+∠DGC=90°,
∵∠FGC=90°,
∴∠AGH+∠DGC=90°,
∴∠DCG=∠AGH,
∴△CDG∽△GAH;
(2)
解:由翻折得∠EGF=∠EAF,
∴∠AGH=∠DAC=∠DCG,
∵CD=AB=2,AD=4,
∴,
∴DG=CD=×2=1,
∴GA=4-1=3,
∵△CDG∽△GAH,
∴,
∴tan∠GHC=.
2.(1)
证明:∵,,
∴,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是菱形.
(2)
解:∵四边形是菱形,
∴,平分,,
∵平分,,
∴,和都是直角三角形,
∵,,
∴在中,,,
∴,
∴,
∴,
在中,,,
∴,
∴,
∴,
∴.
∴的长为,的长为.
3.(1)
证明:连接AC,如图,
∵四边形ABCD为菱形,
∴,.
∴,为等边三角形.
∴,.
又∵,∴.
∴.
∴.
(2)
解:连接AC,由题意可得:,
①如图,
当G在BC上时,作,交AB于点H.
∴,
∴为等边三角形.
.而
∴,,
∴.
∴.
∵,,,
∴.
②如图,
当G在CD上时,作,交BA的延长线于点H.
∵四边形ABCD为菱形,
∴.
∴四边形ACGH是平行四边形.
∴,
∴.
∵,
∴.
∴.
∴.
∴.
∴.
∵,,,
∴.
综上所述:或.
(3)
分三种情况:
第一种,如图,当G与A重合时,过作于F,连接EF,
为的中点,
四边形为平行四边形,
,
所以此时
第二种,①如图,当F与A重合,且时,
同理:四边形是平行四边形,
;
②如图,
结合①把沿折叠,则
此时
结合菱形的性质可得:落在BC上,
此时
第三种,如图,当在上,
过作,
而而为两平行线间的距离,则也为两平行线间的距离,
过作于
则
为等边三角形,
综上:的长为2,4或.
4.(1)
解:(1)由题意可知,
∵,
∴.
∵,,
∴,
∴.
(2)
证明:∵,
∴,
∵,
∴.
∵,
∴.
∵,
∴,
∴,
∴.
(3)
解:∵,
∴.
∵,
∴,
∴.
∵,
∴△MCE为等腰直角三角形,
.
在Rt△BEC中,,
∴.
5.(1)
解:∵AB∥CE,
∴∠BAD=∠DEC,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠CAD=∠DEC,
∴AC=EC,
∵∠BDA=∠CDE,
∴,
∴,
即,
∴;
(2)
①由折叠可知,AD平分∠BAC,CD=DE,
由(1)得,,
∵AC=1,AB=2,
∴,
∴,
解得:CD=,
∴DE= CD=;
②由折叠可知∠AED=∠C=,
∴,
由①可知,
∴,
∴,
即:.
6.(1)
解:在矩形中,,AD∥BC
∵点为中点,
∴,
在和中,
,
∴;
∴∠AEB=∠DEC,
∵,
∴∠AEB+∠DEC=2∠AEB=180°-∠BEC=90°,
∴∠AEB=45°,
∵AD∥BC,
∴∠EBC=AEB=45°;
(2)
证明:在矩形中,,
∴∠AEB=∠EBC,
∵∠BEC=∠A=90°,
∴△ABE∽△ECB,
∴,
∵,
∴,
∵平分,
∴∠EBG=∠CBF,
∵,
∴△BEG∽△BCF,
∴,
∴,
∴;
(3)
解:过点F作FH⊥BE,交BE延长线于H,连接,如图,
∵,FH⊥BE,
∴,
∴,
∵平分,
∴∠HBF=∠CBF,
在△BHF和△BCF中,
,
∴△BHF≌△BCF(AAS),
∴BH=BC,,HF=CF,
∴,
∴,
在△BHG和△BCG中,
,
∴△BHG≌△BCG(SAS),
∴HG=CG,
∴四边形为菱形,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴.
7.(1)
①.
证明:∵PE平分,
∴,
∴,
又∵,
∴,
∴.
②∵,
∴,
∵,
∴,,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,,
∴由勾股定理得,
∴,
∴,,
将沿PH翻折,使得点B落在AB边上的点D处,
,
,
∴.
(2)
如图,
取AB的中点F,连接CF,
,
∴,,
∴,
∵,
∴,
∴,
∴,
,
,
,
∴,
∴,
∴,
∴.
8.(1)
连接AD,
,点D是的中点,
,,
,
,
,即,
,
,
,
在和中,又,
,
,
,
,
,
故答案为:45°,;
(2)
连接AD,
,点D是的中点,
,
,
,
,
,
,
,
,
,
;
(3)
当点F是AE的中点时,如图
,
在中,根据勾股定理得,
即,
,
,
;
当点E是AF的中点时,如图,连接AD,
,
,
在中,根据勾股定理得,
即,
,
,
;
综上,的长为或.
