九年级数学下册试题 3.6 直线和圆的位置关系 北师大版(含答案)
文档属性
| 名称 | 九年级数学下册试题 3.6 直线和圆的位置关系 北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 19:52:57 | ||
图片预览




文档简介
3.6 直线和圆的位置关系
第一课时
一、单选题
1.在中,,,,以点C为圆心,2cm长为半径的圆与AB的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.下列直线是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.垂直于圆的半径的直线 D.过圆直径外端点的直线
3.在平面直角坐标系中有点A(3,4),以点A为圆心,5为半径画圆,在同一坐标系中直线y=-x与⊙A的位置关系是( )
A.相离 B.相切 C.相交 D.以上都有可能
4.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
5.已知⊙O的半径为3 cm,点P是直线上一点,OP长为5 cm,则直线与⊙O的位置关系为( )
A.相交 B.相切
C.相离 D.相交、相切、相离都有可能
6.如图,已知的直径与弦的夹角为,过点的切线与的延长线交于点,,则的半径为( )
A. B. C. D.
7.如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是( )
A.30° B.45° C.60° D.40°
8.如图,是⊙O的直径,交⊙O于点,于点,下列说法不正确的是( )
A.若,则是⊙O的切线 B.若,则是⊙O的切线
C.若,则是⊙O的切线 D.若是⊙O的切线,则
9.如图,在平面直角坐标系中, ⊙O的半径是1,直线AB与x轴交于点P(x,0),且与x轴的正半轴夹角为45°,若直线AB与⊙O有公共点,则x值的范围是( )
A. B. C. D.
10.如图,的圆心的坐标为,半径为1,直线的表达式为,是直线上的动点,是上的动点,则的最小值是( )
A. B. C. D.
二、填空题
11.在△ABO中,若OA=OB=2,⊙O的半径为1,当∠AOB满足____________时,直线AB与⊙O相切;当∠AOB满足____________时,直线AB与⊙O相交;当∠AOB满足____________时,直线AB与⊙O相离.
12.在Rt△ABC中,∠C=90°,AC=3,BC=4.若以A为圆心、R为半径所作的圆与线段BC只有一个公共点,则R的取值范围是________.
13.已知,P是OA上的一点,cm,以r为半径作⊙P,若cm,则⊙P与的位置关系是_____,若⊙P与相离,则r满足的条件是_____.
14.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.动点O在边CA上移动,且⊙O的半径为2.
(1)若圆心O与点C重合,则⊙O与直线AB________; (2)当OC等于________时,⊙O与直线AB相切.
15.如图,直线AB,CD相交于点O,,圆P的半径为1cm,动点P在直线AB上从点O左侧且距离O点6cm处,以1cm/s的速度向右运动,当圆P与直线CD相切时,圆心P的运动时间为 _____s.
16.在Rt△ABC中,∠ACB=90°,AC=6,BC=8,若以点C为圆心,r为半径的圆与边AB所在直线相离,则r的取值范围为 _____;若⊙C与AB边只有一个有公共点,则r的取值范围为 _____.
17.如图,已知⊙P的半径为1,圆心P在抛物线y=x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为__________________.
18.如图,为的直径,、为上的点,连接、、、,为延长线上一点,连接,且,.若的半径为,则点到的距离为________.
三、解答题
19.如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于点O,D为AB上的一点,OD=OC,以O为圆心,OB的长为半径作⊙O.
(1)求证:AC是⊙O的切线;
(2)若AB=6,BD=2,求线段AC的长.
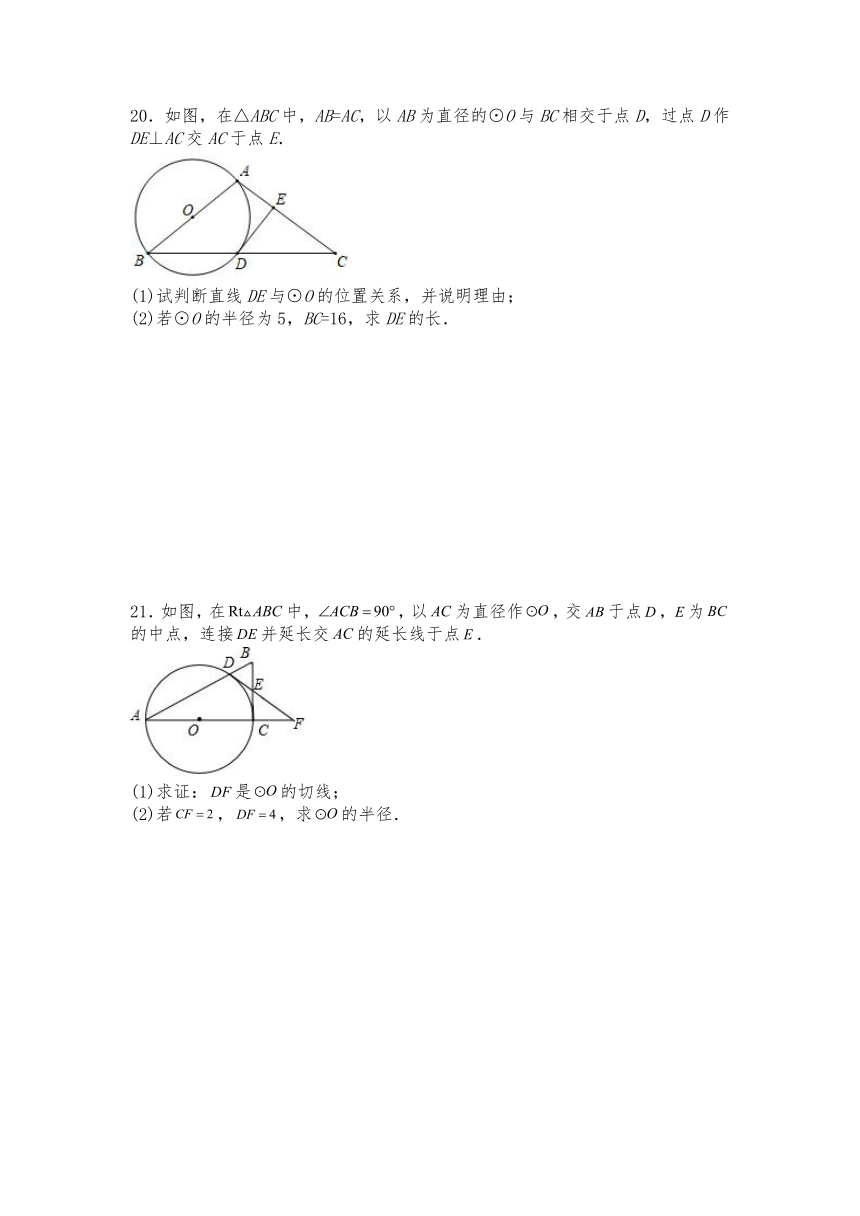
20.如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,过点D作DE⊥AC交AC于点E.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为5,BC=16,求DE的长.
21.如图,在中,,以为直径作,交于点,为的中点,连接并延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径.
22.如图,以线段为直径作,交射线于点,平分交于点,过点作直线于点,交的延长线于点.连接并延长交于点.
(1)求证:直线是的切线;
(2)求证:;
(3)若,,求的长.
第二课时
一、单选题
1.已知,以点为圆心,以为半径画圆,以点为圆心,半径为,画圆已知与外离,则的取值范围为( )
A.0 B.0 C.0 D.0
2.如图,PA切于点A,连接OP交于点B,,点C在上(点B,C在直径AO同侧),连接OC,AC,AB,当时,∠BAC等于( )
A.20° B.25° C.30° D.50°
3.如图,已知点A(-8,0),B(2,0),点C在直线上,则使是直角三角形的点C的个数为( )
A.4 B.3 C.2 D.1
4.如图,中,是的直径,交于点,交于点,点是中点,的切线交于点,则下列结论中①;②;③;④是中点,正确的个数是( )
A.1 B.2 C.3 D.4
5.如图,是⊙O的切线,点A为切点,BO交⊙O于点C,BO的延长线交⊙O于点D,点E在优弧CDA上,连接AD、AE、CE,若∠BAD=122°,则∠CEA的度数为( )
A.26° B.32° C.64° D.128°
6.如图,点C在以AB为直径的半圆上,AB=8,,点D在线段AB上运动,点E与点D关于AC对称,DFDE于点D,并交EC的延长线于点F,下列结论:①CE=CF;②线段EF的最小值为;③当AD=2时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=.其中正确结论的序号是( ).
A.①③ B.②③ C.①②③ D.①②③④
二、填空题
7.在平面直角坐标系中,以点A(﹣2,3)为圆心、r为半径的圆与坐标轴恰好有三个公共点,那么r的值为_____.
8.如图,已知Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是边AB上的动点,Q是边BC上的动点,且∠CPQ=90°,则线段CQ的取值范围是____.
9.如图,把置于平面直角坐标系中,点A的坐标为,点B的坐标为,点P是内切圆的圆心.将沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为,第二次滚动后圆心为,…,依此规律,第2019次滚动后,内切圆的圆心的坐标是________.
10.如图,在矩形ABCD中,,,为AD上一点,且,为BC边上的动点,以为EF直径作,当与矩形的边相切时,BF的长为______.
11.如图,在中,,.点为线段上一动点,当点运动到某一位置时,它到点,的距离都等于,到点的距离等于的所有点组成的图形为,点为线段延长线上一点,且点到点的距离也等于.则直线与图形有______个公共点.
12.在中,,,以边的中点为圆心,作半圆与相切,点分别是边和半圆上的动点,连接,则长的最大值与最小值的和是__________.
三、解答题
13.如图,在中,以为直径作交于点,交于点,且是中点,,垂足为,交的延长线于点.
(1)求证:直线是的切线;
(2),,求的长.
14.数学活动——旋转变换
(1)如图①,在中,,将绕点C逆时针旋转50°得到,连接,求的大小;
(2)如图②,在中,,,,将绕点C逆时针旋转60°得到,连接,以为圆心,长为半径作圆.
①猜想:直线与的位置关系,并证明你的结论;
②连接,线段的长度为______.
15.如图,AB是半圆形量角器的直径,点O为半圆的圆心,DA与半圆O相切于点A,点P在半圆上,且点P对应的示数为120°(60°),点C是上一点(不与点P重合).连接DO交半圆O于点E,点E对应的示数为60°(120°).
(1)连接PC,AC,求∠PCA的度数;
(2)连接AP,PB,求证:△DAO≌△APB;
(3)若直径AB上存在一点M,使得EM+PM的值最小,已知半圆O的半径是2,直接写出EM+PM的最小值.
16.如图,内接于,,为直径,与相交于点,过点作,垂足为,延长交的延长线于点,连接.
(1)求证:与相切:
(2)若,求的值;
(3)在(2)的条件下,若的半径为4,,求的长.
17.在平面坐标系中,给出如下定义:若点在图形上,点在图形上,称线段长度的最小值为图形、的“最近距离”,记为.特别地,若图形、有公共点,规定值为0.
(1)如图1,的半径为2,
①点,则_________.
②记反比例函数的图像为,则_________.
(2)如图2,点,的半径为1,直线:,若,求的值.
(3)如图3,直线:与轴交于点,与轴交于点,边长为2的正方形的中心为,将正方形沿着轴的正半轴向右平移个单位,记正方形为图形,若线段与正方形的“最近距离”满足,请直接写出的取值范围.
第一课时答案
一、单选题
C.B.C.B.D.A .A.A.B.A.
二、填空题
11. ∠AOB=120° 120°<∠AOB<180° 0°<∠AOB<120°
12.3≤R≤5
13.相离;.
14. 相离
15.4或8.
16.017.(2,1)或(﹣2,1)或(0,﹣1).
18.
三、解答题
19.(1)
证明:过O作OE⊥AC于E.
∵AO平分∠BAC,且∠ABC=90°,OE⊥AC,
∴OB=OE,即OE为圆的半径,
∴AC是⊙O的切线;
(2)
∵∠ABC=90°,OB为⊙O半径,
∴AB是⊙O的切线,
又由(1)AC是⊙O的切线,
∴AB=AE=6,
在Rt△BOD和Rt△COE中,
,
∴Rt△BOD≌Rt△COE,
∴BD=CE=2,
∴AC=AE+CE=8
20.(1)
解:DE是⊙O的切线,理由如下:
连接OD,
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)
解:连接AD,
∵∠ADB=90°,AB=AC,
∴BD=CD,
∵⊙O的半径为5,BC=16,
∴AC=AB=10,CD=8,
∴AD= ,
∵S△ADC=AC DE=AD CD,
∴DE=.
21.(1)
解:如图,连接OD、CD.
∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠CDB=90°,即△BCD是直角三角形,
∵E为BC的中点,
∴BE=CE=DE,
∴∠CDE=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠DCE=90°,
∴∠ODC+∠CDE=90°,即OD⊥DE,
∴DE是⊙O的切线;
(2)
解:设⊙O的半径为r,
∵∠ODF=90°,
∴OD2+DF2=OF2,即r2+42=(r+2)2,
解得:r=3,
∴⊙O的半径为3.
22.(1)
证明:连接OD,则OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴ODAC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE是⊙O的切线.
(2)
证明:线段是的直径,
,
∴∠ADM=180°-∠ADB=,
∴∠M+∠DAM=,∠ABM+∠DAB=,
∵∠DAM=∠DAB,
∴∠M=∠ABM,
∴AB=AM.
(3)
解:∵∠AEF=90°,∠F=30°,
∴∠BAM=60°,
∴△ABM是等边三角形,
∴∠M=60°,
∵∠DEM=90°,ME=1,
∴∠EDM=30°,
∴MD=2ME=2,
∴BD=MD=2,
∵∠BDF=∠EDM=30°,
∴∠BDF=∠F,
∴BF=BD=2.
第二课时答案
一、单选题
C.B.A.C.B.A.
二、填空题
7.3或
8.≤CQ≤12.
9.(8077,1).
10.2或或
11.1.
12.9.
三、解答题
13.(1)证明:连结OD,
∵点O为AC中点,点D为BC中点,
∴OD为△CAB的中位线,
∴OD∥AB,
∵,
∴
∴直线是的切线;
(2)解:∵OD∥AB,OC=OD,
∴∠FOD=∠A,
∵,
∴,
解得OD=,
∵OD为△CAB的中位线,
∴AB=2OD=,
∵AC=2OC=2OD=,
∴AF=FC+AC=5+,
∴AE=AF,
∴BE=AB- AE=2.
14.(1)
解:如图①中,∵是由旋转得到,
∴,,
∴,
∵,
∴,
∴.
(2)
解:①结论:直线是的切线.
理由:如图②中,∵,,
∴,
∵,
∴,
∴.
∴,
∴直线、是的切线;
②在中,=90°,B=BC=5,A=AB=3,
由勾股定理得,B=.
15.(1)
连接AP,OP,
根据题意可知,∠AOP = 120°
所对的圆心角为∠AOP,
∴ ∠PCA=∠AOP = 60°;
(2)
连接PO,
根据题意可知,∠AOE= ∠BOP = 60°,
∵BO = PO,
∴ΔBOP是等边三角形,
∴PB = OB,∠ABP = ∠AOD = 60°,
∵AO = OB,
∴AO = BP ,
∵AB是直径,
∴∠APB = 90°,
∵AD是OO的切线,
∴∠OAD = 90°,
∴∠OAD =∠APB,
在ΔDAO和ΔAPB中
∴;
(3)
作点E关于直线AB对称的对称点E',连接E'O,PO,
根据对称性可知EO =E'O =2,
根据题意可知∠AOE= 60°,
∵AO = EO,
∴ΔΑΕΟ是等边三角形,
∴∠AEO = 60°,
∵ΕΕ'⊥AO,
∴∠ΟEE'= ∠AEO = 30°,
∴∠EE'O =∠OEE'= 30°,
∴∠EΟE'= 120°,
∵∠AOE =∠BOP = 60°,
∴∠EOP = 180°-∠AOE-∠BOP=60°,
∴∠EOP + ∠EOE'=180°,
∴E'、O、P在同一条直线上,
∴当点M与点O重合时,EM+PM为最小值,此时EM+PM = E'P = 2+ 2 = 4.
16.(1)证明:如图,连接,
∵,
,
、,
,
是的直径,
∴∠DBC=90°,
,
,
,
与相切;
(2)解:过点作于点,连接,
∵OC=OA,,
∴,
,
,
∴∠EBF=∠AOM,
又,
,
,
,,
,
又,
;
(3)解:,,
,
在中,,
又,
是等边三角形,
,
,,
,
∴EC=2EF,由勾股定理FC=
设,则、,
,
,且,
,
在中,,
,
整理得
△=242-16×23=208>0
解得:,
,舍去,
,
.
17.(1)解:①∵半径为2,,
∴,
故答案为:1;
②设与x轴交于点B,与y轴交于点C,过点B作轴,过C点作轴,与交于点D,
∴,
∵D点在函数图象上,
连接OD交于E,
∴,
∴,
故答案为:;
(2)解:设直线与x轴交于点A,与y轴交于点C,过B点作于D,
∴,
∴,
∵,
∴,
∴,
即,
解得或,
∴k的值为2或;
(3)解:如下图所示,当正方形处在图中虚线两个位置时,
作于M,的运动路径交于P,
∴,
由平移可知:,
∴,
由直线解析式,得时,,
∴,
当时,,
解得,
∴,
∵正方形的边长为2,中心O,
∴,
∴,
∴,
∴,
∴点E平移到处,,
点H平移到右面虚线位置处,,
∴m的取值范围为.
第一课时
一、单选题
1.在中,,,,以点C为圆心,2cm长为半径的圆与AB的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.下列直线是圆的切线的是( )
A.与圆有公共点的直线 B.到圆心的距离等于半径的直线
C.垂直于圆的半径的直线 D.过圆直径外端点的直线
3.在平面直角坐标系中有点A(3,4),以点A为圆心,5为半径画圆,在同一坐标系中直线y=-x与⊙A的位置关系是( )
A.相离 B.相切 C.相交 D.以上都有可能
4.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
5.已知⊙O的半径为3 cm,点P是直线上一点,OP长为5 cm,则直线与⊙O的位置关系为( )
A.相交 B.相切
C.相离 D.相交、相切、相离都有可能
6.如图,已知的直径与弦的夹角为,过点的切线与的延长线交于点,,则的半径为( )
A. B. C. D.
7.如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是( )
A.30° B.45° C.60° D.40°
8.如图,是⊙O的直径,交⊙O于点,于点,下列说法不正确的是( )
A.若,则是⊙O的切线 B.若,则是⊙O的切线
C.若,则是⊙O的切线 D.若是⊙O的切线,则
9.如图,在平面直角坐标系中, ⊙O的半径是1,直线AB与x轴交于点P(x,0),且与x轴的正半轴夹角为45°,若直线AB与⊙O有公共点,则x值的范围是( )
A. B. C. D.
10.如图,的圆心的坐标为,半径为1,直线的表达式为,是直线上的动点,是上的动点,则的最小值是( )
A. B. C. D.
二、填空题
11.在△ABO中,若OA=OB=2,⊙O的半径为1,当∠AOB满足____________时,直线AB与⊙O相切;当∠AOB满足____________时,直线AB与⊙O相交;当∠AOB满足____________时,直线AB与⊙O相离.
12.在Rt△ABC中,∠C=90°,AC=3,BC=4.若以A为圆心、R为半径所作的圆与线段BC只有一个公共点,则R的取值范围是________.
13.已知,P是OA上的一点,cm,以r为半径作⊙P,若cm,则⊙P与的位置关系是_____,若⊙P与相离,则r满足的条件是_____.
14.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.动点O在边CA上移动,且⊙O的半径为2.
(1)若圆心O与点C重合,则⊙O与直线AB________; (2)当OC等于________时,⊙O与直线AB相切.
15.如图,直线AB,CD相交于点O,,圆P的半径为1cm,动点P在直线AB上从点O左侧且距离O点6cm处,以1cm/s的速度向右运动,当圆P与直线CD相切时,圆心P的运动时间为 _____s.
16.在Rt△ABC中,∠ACB=90°,AC=6,BC=8,若以点C为圆心,r为半径的圆与边AB所在直线相离,则r的取值范围为 _____;若⊙C与AB边只有一个有公共点,则r的取值范围为 _____.
17.如图,已知⊙P的半径为1,圆心P在抛物线y=x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为__________________.
18.如图,为的直径,、为上的点,连接、、、,为延长线上一点,连接,且,.若的半径为,则点到的距离为________.
三、解答题
19.如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于点O,D为AB上的一点,OD=OC,以O为圆心,OB的长为半径作⊙O.
(1)求证:AC是⊙O的切线;
(2)若AB=6,BD=2,求线段AC的长.
20.如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,过点D作DE⊥AC交AC于点E.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为5,BC=16,求DE的长.
21.如图,在中,,以为直径作,交于点,为的中点,连接并延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求的半径.
22.如图,以线段为直径作,交射线于点,平分交于点,过点作直线于点,交的延长线于点.连接并延长交于点.
(1)求证:直线是的切线;
(2)求证:;
(3)若,,求的长.
第二课时
一、单选题
1.已知,以点为圆心,以为半径画圆,以点为圆心,半径为,画圆已知与外离,则的取值范围为( )
A.0 B.0 C.0 D.0
2.如图,PA切于点A,连接OP交于点B,,点C在上(点B,C在直径AO同侧),连接OC,AC,AB,当时,∠BAC等于( )
A.20° B.25° C.30° D.50°
3.如图,已知点A(-8,0),B(2,0),点C在直线上,则使是直角三角形的点C的个数为( )
A.4 B.3 C.2 D.1
4.如图,中,是的直径,交于点,交于点,点是中点,的切线交于点,则下列结论中①;②;③;④是中点,正确的个数是( )
A.1 B.2 C.3 D.4
5.如图,是⊙O的切线,点A为切点,BO交⊙O于点C,BO的延长线交⊙O于点D,点E在优弧CDA上,连接AD、AE、CE,若∠BAD=122°,则∠CEA的度数为( )
A.26° B.32° C.64° D.128°
6.如图,点C在以AB为直径的半圆上,AB=8,,点D在线段AB上运动,点E与点D关于AC对称,DFDE于点D,并交EC的延长线于点F,下列结论:①CE=CF;②线段EF的最小值为;③当AD=2时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=.其中正确结论的序号是( ).
A.①③ B.②③ C.①②③ D.①②③④
二、填空题
7.在平面直角坐标系中,以点A(﹣2,3)为圆心、r为半径的圆与坐标轴恰好有三个公共点,那么r的值为_____.
8.如图,已知Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是边AB上的动点,Q是边BC上的动点,且∠CPQ=90°,则线段CQ的取值范围是____.
9.如图,把置于平面直角坐标系中,点A的坐标为,点B的坐标为,点P是内切圆的圆心.将沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为,第二次滚动后圆心为,…,依此规律,第2019次滚动后,内切圆的圆心的坐标是________.
10.如图,在矩形ABCD中,,,为AD上一点,且,为BC边上的动点,以为EF直径作,当与矩形的边相切时,BF的长为______.
11.如图,在中,,.点为线段上一动点,当点运动到某一位置时,它到点,的距离都等于,到点的距离等于的所有点组成的图形为,点为线段延长线上一点,且点到点的距离也等于.则直线与图形有______个公共点.
12.在中,,,以边的中点为圆心,作半圆与相切,点分别是边和半圆上的动点,连接,则长的最大值与最小值的和是__________.
三、解答题
13.如图,在中,以为直径作交于点,交于点,且是中点,,垂足为,交的延长线于点.
(1)求证:直线是的切线;
(2),,求的长.
14.数学活动——旋转变换
(1)如图①,在中,,将绕点C逆时针旋转50°得到,连接,求的大小;
(2)如图②,在中,,,,将绕点C逆时针旋转60°得到,连接,以为圆心,长为半径作圆.
①猜想:直线与的位置关系,并证明你的结论;
②连接,线段的长度为______.
15.如图,AB是半圆形量角器的直径,点O为半圆的圆心,DA与半圆O相切于点A,点P在半圆上,且点P对应的示数为120°(60°),点C是上一点(不与点P重合).连接DO交半圆O于点E,点E对应的示数为60°(120°).
(1)连接PC,AC,求∠PCA的度数;
(2)连接AP,PB,求证:△DAO≌△APB;
(3)若直径AB上存在一点M,使得EM+PM的值最小,已知半圆O的半径是2,直接写出EM+PM的最小值.
16.如图,内接于,,为直径,与相交于点,过点作,垂足为,延长交的延长线于点,连接.
(1)求证:与相切:
(2)若,求的值;
(3)在(2)的条件下,若的半径为4,,求的长.
17.在平面坐标系中,给出如下定义:若点在图形上,点在图形上,称线段长度的最小值为图形、的“最近距离”,记为.特别地,若图形、有公共点,规定值为0.
(1)如图1,的半径为2,
①点,则_________.
②记反比例函数的图像为,则_________.
(2)如图2,点,的半径为1,直线:,若,求的值.
(3)如图3,直线:与轴交于点,与轴交于点,边长为2的正方形的中心为,将正方形沿着轴的正半轴向右平移个单位,记正方形为图形,若线段与正方形的“最近距离”满足,请直接写出的取值范围.
第一课时答案
一、单选题
C.B.C.B.D.A .A.A.B.A.
二、填空题
11. ∠AOB=120° 120°<∠AOB<180° 0°<∠AOB<120°
12.3≤R≤5
13.相离;.
14. 相离
15.4或8.
16.0
18.
三、解答题
19.(1)
证明:过O作OE⊥AC于E.
∵AO平分∠BAC,且∠ABC=90°,OE⊥AC,
∴OB=OE,即OE为圆的半径,
∴AC是⊙O的切线;
(2)
∵∠ABC=90°,OB为⊙O半径,
∴AB是⊙O的切线,
又由(1)AC是⊙O的切线,
∴AB=AE=6,
在Rt△BOD和Rt△COE中,
,
∴Rt△BOD≌Rt△COE,
∴BD=CE=2,
∴AC=AE+CE=8
20.(1)
解:DE是⊙O的切线,理由如下:
连接OD,
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)
解:连接AD,
∵∠ADB=90°,AB=AC,
∴BD=CD,
∵⊙O的半径为5,BC=16,
∴AC=AB=10,CD=8,
∴AD= ,
∵S△ADC=AC DE=AD CD,
∴DE=.
21.(1)
解:如图,连接OD、CD.
∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠CDB=90°,即△BCD是直角三角形,
∵E为BC的中点,
∴BE=CE=DE,
∴∠CDE=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠DCE=90°,
∴∠ODC+∠CDE=90°,即OD⊥DE,
∴DE是⊙O的切线;
(2)
解:设⊙O的半径为r,
∵∠ODF=90°,
∴OD2+DF2=OF2,即r2+42=(r+2)2,
解得:r=3,
∴⊙O的半径为3.
22.(1)
证明:连接OD,则OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴ODAC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE是⊙O的切线.
(2)
证明:线段是的直径,
,
∴∠ADM=180°-∠ADB=,
∴∠M+∠DAM=,∠ABM+∠DAB=,
∵∠DAM=∠DAB,
∴∠M=∠ABM,
∴AB=AM.
(3)
解:∵∠AEF=90°,∠F=30°,
∴∠BAM=60°,
∴△ABM是等边三角形,
∴∠M=60°,
∵∠DEM=90°,ME=1,
∴∠EDM=30°,
∴MD=2ME=2,
∴BD=MD=2,
∵∠BDF=∠EDM=30°,
∴∠BDF=∠F,
∴BF=BD=2.
第二课时答案
一、单选题
C.B.A.C.B.A.
二、填空题
7.3或
8.≤CQ≤12.
9.(8077,1).
10.2或或
11.1.
12.9.
三、解答题
13.(1)证明:连结OD,
∵点O为AC中点,点D为BC中点,
∴OD为△CAB的中位线,
∴OD∥AB,
∵,
∴
∴直线是的切线;
(2)解:∵OD∥AB,OC=OD,
∴∠FOD=∠A,
∵,
∴,
解得OD=,
∵OD为△CAB的中位线,
∴AB=2OD=,
∵AC=2OC=2OD=,
∴AF=FC+AC=5+,
∴AE=AF,
∴BE=AB- AE=2.
14.(1)
解:如图①中,∵是由旋转得到,
∴,,
∴,
∵,
∴,
∴.
(2)
解:①结论:直线是的切线.
理由:如图②中,∵,,
∴,
∵,
∴,
∴.
∴,
∴直线、是的切线;
②在中,=90°,B=BC=5,A=AB=3,
由勾股定理得,B=.
15.(1)
连接AP,OP,
根据题意可知,∠AOP = 120°
所对的圆心角为∠AOP,
∴ ∠PCA=∠AOP = 60°;
(2)
连接PO,
根据题意可知,∠AOE= ∠BOP = 60°,
∵BO = PO,
∴ΔBOP是等边三角形,
∴PB = OB,∠ABP = ∠AOD = 60°,
∵AO = OB,
∴AO = BP ,
∵AB是直径,
∴∠APB = 90°,
∵AD是OO的切线,
∴∠OAD = 90°,
∴∠OAD =∠APB,
在ΔDAO和ΔAPB中
∴;
(3)
作点E关于直线AB对称的对称点E',连接E'O,PO,
根据对称性可知EO =E'O =2,
根据题意可知∠AOE= 60°,
∵AO = EO,
∴ΔΑΕΟ是等边三角形,
∴∠AEO = 60°,
∵ΕΕ'⊥AO,
∴∠ΟEE'= ∠AEO = 30°,
∴∠EE'O =∠OEE'= 30°,
∴∠EΟE'= 120°,
∵∠AOE =∠BOP = 60°,
∴∠EOP = 180°-∠AOE-∠BOP=60°,
∴∠EOP + ∠EOE'=180°,
∴E'、O、P在同一条直线上,
∴当点M与点O重合时,EM+PM为最小值,此时EM+PM = E'P = 2+ 2 = 4.
16.(1)证明:如图,连接,
∵,
,
、,
,
是的直径,
∴∠DBC=90°,
,
,
,
与相切;
(2)解:过点作于点,连接,
∵OC=OA,,
∴,
,
,
∴∠EBF=∠AOM,
又,
,
,
,,
,
又,
;
(3)解:,,
,
在中,,
又,
是等边三角形,
,
,,
,
∴EC=2EF,由勾股定理FC=
设,则、,
,
,且,
,
在中,,
,
整理得
△=242-16×23=208>0
解得:,
,舍去,
,
.
17.(1)解:①∵半径为2,,
∴,
故答案为:1;
②设与x轴交于点B,与y轴交于点C,过点B作轴,过C点作轴,与交于点D,
∴,
∵D点在函数图象上,
连接OD交于E,
∴,
∴,
故答案为:;
(2)解:设直线与x轴交于点A,与y轴交于点C,过B点作于D,
∴,
∴,
∵,
∴,
∴,
即,
解得或,
∴k的值为2或;
(3)解:如下图所示,当正方形处在图中虚线两个位置时,
作于M,的运动路径交于P,
∴,
由平移可知:,
∴,
由直线解析式,得时,,
∴,
当时,,
解得,
∴,
∵正方形的边长为2,中心O,
∴,
∴,
∴,
∴,
∴点E平移到处,,
点H平移到右面虚线位置处,,
∴m的取值范围为.
