湘教版数学九年级上册 3.4 三角形相似判定 教案
文档属性
| 名称 | 湘教版数学九年级上册 3.4 三角形相似判定 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 204.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-28 00:00:00 | ||
图片预览

文档简介
三角形相似判定(三)教学设计
教学目标:
探索“两边成比例且夹角相等的两个三角形相似”的判定方法,并能运用解题;
2.经历“操作——观察——探索——说理”的数学活动过程,发展合情推理和有条理的表达能力.
教学重点:掌握“两边成比例且夹角相等的两个三角形相似”.
教学难点:
1.“两边成比例且夹角相等的两个三角形相似”的判定方法的证明;
能恰当地运用判定方法判定三角形是否相似.
教学设计
一、我欣赏
介绍几何分形,提出正三角的几何分形会时什么呢?从而引入谢尔宾斯基三角形,提出问题“这些三角形之间有什么关系?为什么?”,提出三角形相似的判定方法除了定义、预备定理、两角相等的外还有那些判定方法呢?
我探究
三角形全等的判定方法有:
ASA AAS SAS SSS HL
SAS :两边相等且夹角相等的两个三角形全等
类比全等三角形的条件(SAS),如果一个三角形的两条边与另一个三角形的两条边对应边的比相等,并且相应的夹角相等,那么这两个三角形一定相似吗?
猜想:两边成比例且夹角相等的两个三角形相似。
同桌合作,一个同学画△ABC且AB=2 cm,BC=3cm,∠B=50°, 另一个同学画△A1B1C1中,A1B1=6cm,B1C1=9cm,∠B1=50°,再比较∠A与∠A1(或∠C与∠C1)的大小。△ABC与△A1B1C1相似吗?为什么?
思考:当我们改变对应边的比值或夹角的时候两个三角形还会相似吗?
已知: ,∠A=∠A'.
求证:△ABC ∽△A'B'C'.
得出结论:两边成比例且夹角相等的两个三角形相似.
我智慧
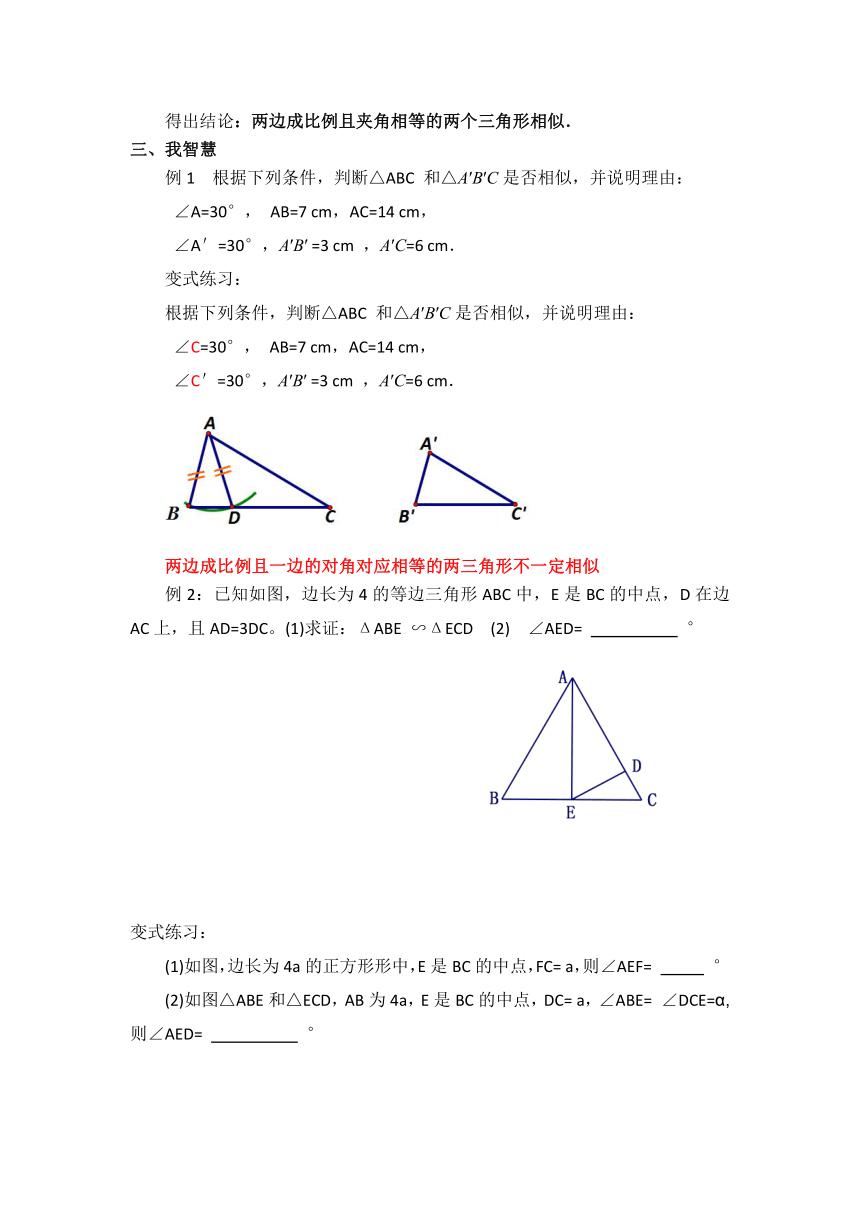
例1 根据下列条件,判断△ABC 和△A′B′C是否相似,并说明理由:
∠A=30°, AB=7 cm,AC=14 cm,
∠A'=30°,A′B′ =3 cm ,A′C=6 cm.
变式练习:
根据下列条件,判断△ABC 和△A′B′C是否相似,并说明理由:
∠C=30°, AB=7 cm,AC=14 cm,
∠C'=30°,A′B′ =3 cm ,A′C=6 cm.
两边成比例且一边的对角对应相等的两三角形不一定相似
例2:已知如图,边长为4的等边三角形ABC中,E是BC的中点,D在边AC上,且AD=3DC。(1)求证:ΔABE ∽ΔECD (2) ∠AED= °
变式练习:
(1)如图,边长为4a的正方形形中,E是BC的中点,FC= a,则∠AEF= °
(2)如图△ABE和△ECD,AB为4a,E是BC的中点,DC= a,∠ABE= ∠DCE=α,则∠AED= °
(3)如图△ABE和△ECD,∠ABE= ∠DCE=∠AED=α,问△ABE与△ECD相似吗?
四、我挑战
1、如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成.利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,这时CD与AB有什么关系?为什么?
2、 如下图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若 ,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似
C.①与④相似 D.②与④相似
五、我收获
通过这节课的学习,你学习到什么新知识?获得了什么数学思想与方法?
六、我提升
1.(必做题)课本第82页习题1、2.
2.(选做题)已知如图五个全等的正方形拼接在一起, 求∠ABC的度数.
3.阅读书籍:《大自然的分形几何学》[波] 伯努瓦·B. 曼德布罗特 / 陈守吉 / 凌复华 / 上海远东出版社 / 1998-12 .
教学目标:
探索“两边成比例且夹角相等的两个三角形相似”的判定方法,并能运用解题;
2.经历“操作——观察——探索——说理”的数学活动过程,发展合情推理和有条理的表达能力.
教学重点:掌握“两边成比例且夹角相等的两个三角形相似”.
教学难点:
1.“两边成比例且夹角相等的两个三角形相似”的判定方法的证明;
能恰当地运用判定方法判定三角形是否相似.
教学设计
一、我欣赏
介绍几何分形,提出正三角的几何分形会时什么呢?从而引入谢尔宾斯基三角形,提出问题“这些三角形之间有什么关系?为什么?”,提出三角形相似的判定方法除了定义、预备定理、两角相等的外还有那些判定方法呢?
我探究
三角形全等的判定方法有:
ASA AAS SAS SSS HL
SAS :两边相等且夹角相等的两个三角形全等
类比全等三角形的条件(SAS),如果一个三角形的两条边与另一个三角形的两条边对应边的比相等,并且相应的夹角相等,那么这两个三角形一定相似吗?
猜想:两边成比例且夹角相等的两个三角形相似。
同桌合作,一个同学画△ABC且AB=2 cm,BC=3cm,∠B=50°, 另一个同学画△A1B1C1中,A1B1=6cm,B1C1=9cm,∠B1=50°,再比较∠A与∠A1(或∠C与∠C1)的大小。△ABC与△A1B1C1相似吗?为什么?
思考:当我们改变对应边的比值或夹角的时候两个三角形还会相似吗?
已知: ,∠A=∠A'.
求证:△ABC ∽△A'B'C'.
得出结论:两边成比例且夹角相等的两个三角形相似.
我智慧
例1 根据下列条件,判断△ABC 和△A′B′C是否相似,并说明理由:
∠A=30°, AB=7 cm,AC=14 cm,
∠A'=30°,A′B′ =3 cm ,A′C=6 cm.
变式练习:
根据下列条件,判断△ABC 和△A′B′C是否相似,并说明理由:
∠C=30°, AB=7 cm,AC=14 cm,
∠C'=30°,A′B′ =3 cm ,A′C=6 cm.
两边成比例且一边的对角对应相等的两三角形不一定相似
例2:已知如图,边长为4的等边三角形ABC中,E是BC的中点,D在边AC上,且AD=3DC。(1)求证:ΔABE ∽ΔECD (2) ∠AED= °
变式练习:
(1)如图,边长为4a的正方形形中,E是BC的中点,FC= a,则∠AEF= °
(2)如图△ABE和△ECD,AB为4a,E是BC的中点,DC= a,∠ABE= ∠DCE=α,则∠AED= °
(3)如图△ABE和△ECD,∠ABE= ∠DCE=∠AED=α,问△ABE与△ECD相似吗?
四、我挑战
1、如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成.利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OD,OB=3OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,这时CD与AB有什么关系?为什么?
2、 如下图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若 ,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似
C.①与④相似 D.②与④相似
五、我收获
通过这节课的学习,你学习到什么新知识?获得了什么数学思想与方法?
六、我提升
1.(必做题)课本第82页习题1、2.
2.(选做题)已知如图五个全等的正方形拼接在一起, 求∠ABC的度数.
3.阅读书籍:《大自然的分形几何学》[波] 伯努瓦·B. 曼德布罗特 / 陈守吉 / 凌复华 / 上海远东出版社 / 1998-12 .
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
