三角形全等的判定(SAS)导学案
文档属性
| 名称 | 三角形全等的判定(SAS)导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 109.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-12 00:00:00 | ||
图片预览

文档简介
136导学案——八年级数学(上)
编号: 班级: 姓名:
课题:三角形全等的判定(SAS)
主备: 审核: 时间:2014年 月 第 周
一、教学目标:
1、掌握“边角边”条件的内容
2、能应用“边角边”条件判定两个三角形全等
3、通过探究三角形全等的条件的活动,激发学生的学习兴趣
教学重点:“边角边”条件
教学难点:指导学生分析问题,寻找判定三角形全等的条件
教学过程:
二、自主预习:
1、两边和它们的夹角对应相等的两个三角形_________,可以简写成_____或_______.
2、在△ABC与△中,如果AB=,BC=,若要得到
△ABC≌△,还需要一个条件,这个条件是______,你的依据是_____。
3、如图,使△ABC≌△ADC成立的条件是( )
A、AB=AD,∠B=∠D
B、AB=AD,∠ACB=∠ACD
C、BC=DC,∠BAC=∠DAC
D、AB=AD,∠BAC=∠DAC
4、根据下列条件能画出唯一的△ABC的是( )
A、AB=3,AC=4,BC=8 B、AB=4,BC=3,∠A=30°
C、AB=5,AC=6,∠A=45° D、∠A=30°,∠B=60°,∠C=90°
5、如图,点E在线段AB上,AC=AD,∠CAB=
∠DAB,则图中全等的三角形有_________________
____________________________(用“≌”表示)
三、合作探究:
1、复习思考
(1)怎样的两个三角形是全等三角形?全等三角形的性质是什么?三角形全等的判定(一)的内容是什么?
(2)上节课我们知道满足三个条件画两个三 ( http: / / www.21cnjy.com )角形有4种情形,三个角对应相等;三条边对应相等;两角和一边对应相等;两边和一角对应相等;前两种情况已经研究了,今天我们来研究第三种两边和一角的情况,这种情况又要分两边和它们的夹角,两边及其一边的对角两种情况。
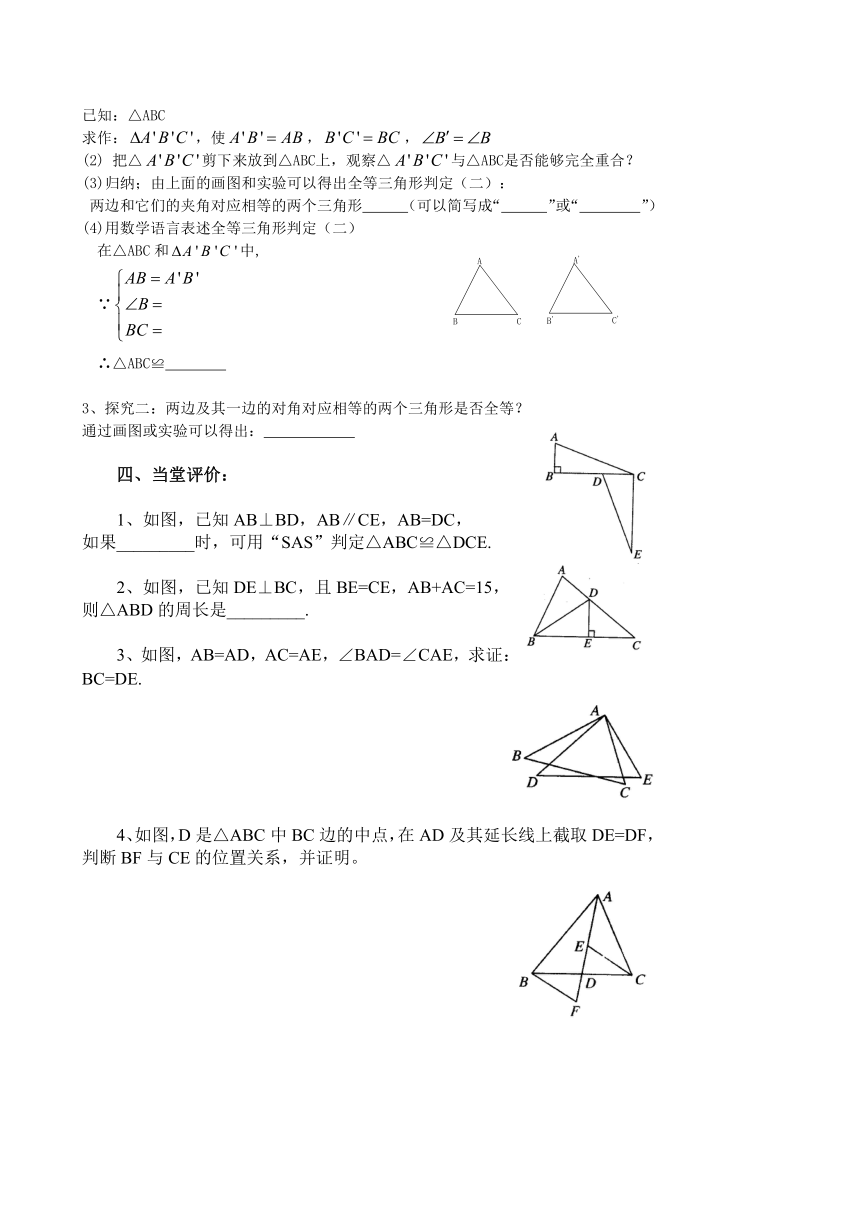
2、探究一:两边和它们的夹角对应相等的两个三角形是否全等?
(1)动手试一试
已知:△ABC
求作:,使,,
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(二):
两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(二)
在△ABC和中,
∵
∴△ABC≌
3、探究二:两边及其一边的对角对应相等的两个三角形是否全等?
通过画图或实验可以得出:
四、当堂评价:
如图,已知AB⊥BD,AB∥CE,AB=DC,
如果_________时,可用“SAS”判定△ABC≌△DCE.
2、如图,已知DE⊥BC,且BE=CE,AB+AC=15,
则△ABD的周长是_________.
3、如图,AB=AD,AC=AE,∠BAD=∠CAE,求证:BC=DE.
( http: / / www.21cnjy.com )
4、如图,D是△ABC中BC边的中点,在AD及其延长线上截取DE=DF,判断BF与CE的位置关系,并证明。
( http: / / www.21cnjy.com )
五、拓展提升:
1、如图,在△ABC中,AB=5,AC=3,AD是BC边上的中线,求AD的取值范围。
( http: / / www.21cnjy.com )
2、两个大小不同的等腰直角三角形三角板,如图(1)所示放置,图(2)是由它抽象出的几何图形,B、C、E在同一直线上连结DC,
(1)请找出图(2)中的全等三角形,并给予证明。
(2)试猜想DC与BE的位置关系,并证明你的结论。
( http: / / www.21cnjy.com )
六、课后评价:
1、如图,F、E是线段BC上的两点,且∠B=∠C,AB=DC,要使△ABE≌△DCF,若从SAS考虑,则需要添加条件_________。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第1题图 第2题图 第3题图 第4题图
2、如图所示,有一块三角形镜子,小明不小心将它打破成1、2两块,现需配成同样大小的一块,为了方便起见,需带上__块,其理由是______。
3、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=70°,
∠B=30°,则∠EOB的度数为_______.
4、如图,已知∠1=∠2,要判定△ABC≌△ADE,还需加上条件( )
A、AB=AD,AC=AE B、AB=AD,BC=DE
C、AC=AE,BC=DE D、无法确定
5、如图1,已知在△ABC中,AB=AC, ( http: / / www.21cnjy.com )P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠ABC连接BQ、CP,求证BQ=CP.
( http: / / www.21cnjy.com )
如图2,若点P是△ABC外一点,其余的条件和操作不变,BQ=CP还成立吗?若成立,给予证明,若不成立,说明理由。
( http: / / www.21cnjy.com )
6、如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC,
(1)求证:△ABE≌△CBD
(2)若∠CAE=30°,求∠BDC的度数。
( http: / / www.21cnjy.com )
七、课堂小结:这堂课学到了什么?(学生总结)
八、教学反思:
编号: 班级: 姓名:
课题:三角形全等的判定(SAS)
主备: 审核: 时间:2014年 月 第 周
一、教学目标:
1、掌握“边角边”条件的内容
2、能应用“边角边”条件判定两个三角形全等
3、通过探究三角形全等的条件的活动,激发学生的学习兴趣
教学重点:“边角边”条件
教学难点:指导学生分析问题,寻找判定三角形全等的条件
教学过程:
二、自主预习:
1、两边和它们的夹角对应相等的两个三角形_________,可以简写成_____或_______.
2、在△ABC与△中,如果AB=,BC=,若要得到
△ABC≌△,还需要一个条件,这个条件是______,你的依据是_____。
3、如图,使△ABC≌△ADC成立的条件是( )
A、AB=AD,∠B=∠D
B、AB=AD,∠ACB=∠ACD
C、BC=DC,∠BAC=∠DAC
D、AB=AD,∠BAC=∠DAC
4、根据下列条件能画出唯一的△ABC的是( )
A、AB=3,AC=4,BC=8 B、AB=4,BC=3,∠A=30°
C、AB=5,AC=6,∠A=45° D、∠A=30°,∠B=60°,∠C=90°
5、如图,点E在线段AB上,AC=AD,∠CAB=
∠DAB,则图中全等的三角形有_________________
____________________________(用“≌”表示)
三、合作探究:
1、复习思考
(1)怎样的两个三角形是全等三角形?全等三角形的性质是什么?三角形全等的判定(一)的内容是什么?
(2)上节课我们知道满足三个条件画两个三 ( http: / / www.21cnjy.com )角形有4种情形,三个角对应相等;三条边对应相等;两角和一边对应相等;两边和一角对应相等;前两种情况已经研究了,今天我们来研究第三种两边和一角的情况,这种情况又要分两边和它们的夹角,两边及其一边的对角两种情况。
2、探究一:两边和它们的夹角对应相等的两个三角形是否全等?
(1)动手试一试
已知:△ABC
求作:,使,,
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(二):
两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(二)
在△ABC和中,
∵
∴△ABC≌
3、探究二:两边及其一边的对角对应相等的两个三角形是否全等?
通过画图或实验可以得出:
四、当堂评价:
如图,已知AB⊥BD,AB∥CE,AB=DC,
如果_________时,可用“SAS”判定△ABC≌△DCE.
2、如图,已知DE⊥BC,且BE=CE,AB+AC=15,
则△ABD的周长是_________.
3、如图,AB=AD,AC=AE,∠BAD=∠CAE,求证:BC=DE.
( http: / / www.21cnjy.com )
4、如图,D是△ABC中BC边的中点,在AD及其延长线上截取DE=DF,判断BF与CE的位置关系,并证明。
( http: / / www.21cnjy.com )
五、拓展提升:
1、如图,在△ABC中,AB=5,AC=3,AD是BC边上的中线,求AD的取值范围。
( http: / / www.21cnjy.com )
2、两个大小不同的等腰直角三角形三角板,如图(1)所示放置,图(2)是由它抽象出的几何图形,B、C、E在同一直线上连结DC,
(1)请找出图(2)中的全等三角形,并给予证明。
(2)试猜想DC与BE的位置关系,并证明你的结论。
( http: / / www.21cnjy.com )
六、课后评价:
1、如图,F、E是线段BC上的两点,且∠B=∠C,AB=DC,要使△ABE≌△DCF,若从SAS考虑,则需要添加条件_________。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第1题图 第2题图 第3题图 第4题图
2、如图所示,有一块三角形镜子,小明不小心将它打破成1、2两块,现需配成同样大小的一块,为了方便起见,需带上__块,其理由是______。
3、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=70°,
∠B=30°,则∠EOB的度数为_______.
4、如图,已知∠1=∠2,要判定△ABC≌△ADE,还需加上条件( )
A、AB=AD,AC=AE B、AB=AD,BC=DE
C、AC=AE,BC=DE D、无法确定
5、如图1,已知在△ABC中,AB=AC, ( http: / / www.21cnjy.com )P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠ABC连接BQ、CP,求证BQ=CP.
( http: / / www.21cnjy.com )
如图2,若点P是△ABC外一点,其余的条件和操作不变,BQ=CP还成立吗?若成立,给予证明,若不成立,说明理由。
( http: / / www.21cnjy.com )
6、如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC,
(1)求证:△ABE≌△CBD
(2)若∠CAE=30°,求∠BDC的度数。
( http: / / www.21cnjy.com )
七、课堂小结:这堂课学到了什么?(学生总结)
八、教学反思:
