华师大版数学九年级下册 27.2.2 直线与圆的位置关系第2课时 圆的切线的判定与性质课件(12张PPT)
文档属性
| 名称 | 华师大版数学九年级下册 27.2.2 直线与圆的位置关系第2课时 圆的切线的判定与性质课件(12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 364.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-29 10:11:40 | ||
图片预览




文档简介
(共12张PPT)
27.2.2 直线与圆的位置关系
第 2 课时 圆的切线的判定与性质
一
学习目标
1.会过圆上一点作圆的切线,理解切线的判定与性质定理.
2.经历圆的切线判定定理和性质定理的推导,能区分切线判定和性质定理的应用.
二
重难点
重点:掌握圆的切线的判定和性质定理的综合应用.
难点:区分并应用圆的切线的判定和性质定理进行解答和证明.
1.知识回顾
三
教学过程
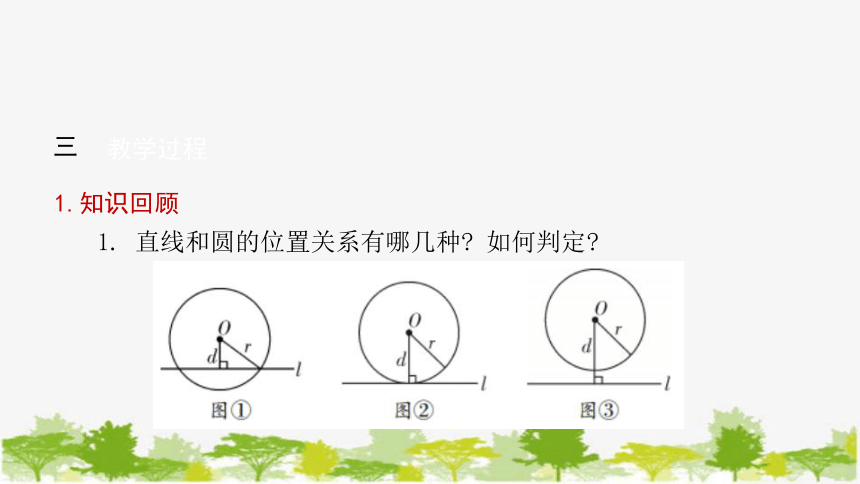
1. 直线和圆的位置关系有哪几种 如何判定
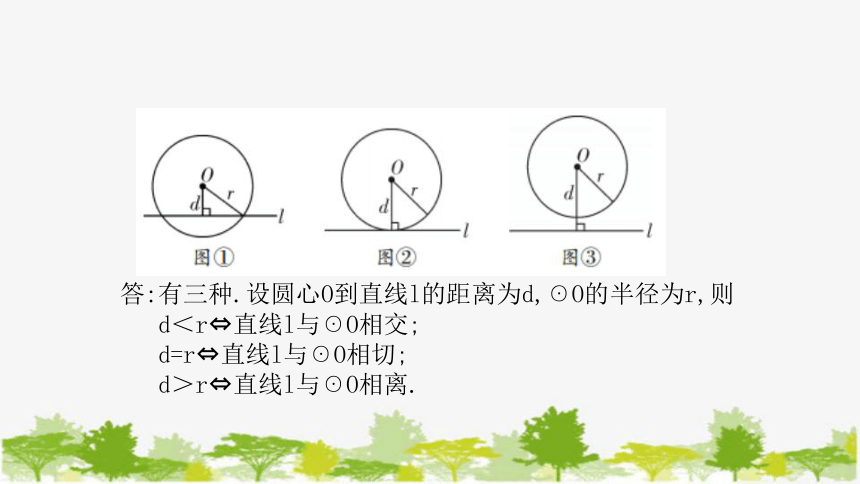
答:有三种.设圆心O到直线l的距离为d,☉O的半径为r,则
d<r 直线l与☉O相交;
d=r 直线l与☉O相切;
d>r 直线l与☉O相离.
2.探究新知
问题 1 如图,在☉O中,经过半径OA的外端点A作直线l⊥OA,直线l和☉O有几个公共点
答:从图可以看出,对直线l上除点A外的任一点P,必有OP>OA,即点P位于圆外,从而可知直线与圆只有一个公共点.
【知识归纳】
切线的判定定理:经过圆的半径的外端且垂直于这条半径 的直线是圆的切线. 这也是过圆上一点作圆的切线的方法.
问题 2 如果直线l是☉O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢
答:由于l是☉O的切线,圆心O到直线l的距离等于半径,所以半径OA是圆心O到直线l的垂线段,即l⊥OA..
【知识归纳】
切线的性质定理:圆的切线垂直于经过切点的半径.
3.例题精讲
例 1 如图,直线AB经过☉O上的点A,且AB=OA,∠OBA=45°.
求证:直线AB是☉O的切线.
证明:∵AB=OA,∠OBA=45°,
∴∠AOB=∠OBA=45°,
∴∠OAB = 90°.
又∵点 A 在圆上,
∴直线AB是☉O的切线.
例 2 如图,在△ABC中,AB=AC,点O在边AB上,☉O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为点F.求证:直线EF是☉O的切线.
证明:连结OE,∵AB=AC,OB=OE,
∴∠B=∠C,∠B=∠OEB,∴∠C=∠OEB,
∴OE∥AC,∴∠OEF=∠EFC.
∵EF⊥AC,∠EFC=90°,∴∠OEF=90°,
∴OE⊥EF.∴EF是☉O的切线.
4.巩固练习 完成教材课后同步练习
5.课堂小结与反思
小结:1.用圆的切线时,常常连结圆心和切点证明切线垂直于半径.
2.“连半径,证垂直”与“作垂直,证半径”是判定直线与圆相切
常用的两种方法.
反思:经历探究切线的判定定理和性质定理的过程,掌握切线的基础知识和基本技能,并能解决简单的问题.
27.2.2 直线与圆的位置关系
第 2 课时 圆的切线的判定与性质
一
学习目标
1.会过圆上一点作圆的切线,理解切线的判定与性质定理.
2.经历圆的切线判定定理和性质定理的推导,能区分切线判定和性质定理的应用.
二
重难点
重点:掌握圆的切线的判定和性质定理的综合应用.
难点:区分并应用圆的切线的判定和性质定理进行解答和证明.
1.知识回顾
三
教学过程
1. 直线和圆的位置关系有哪几种 如何判定
答:有三种.设圆心O到直线l的距离为d,☉O的半径为r,则
d<r 直线l与☉O相交;
d=r 直线l与☉O相切;
d>r 直线l与☉O相离.
2.探究新知
问题 1 如图,在☉O中,经过半径OA的外端点A作直线l⊥OA,直线l和☉O有几个公共点
答:从图可以看出,对直线l上除点A外的任一点P,必有OP>OA,即点P位于圆外,从而可知直线与圆只有一个公共点.
【知识归纳】
切线的判定定理:经过圆的半径的外端且垂直于这条半径 的直线是圆的切线. 这也是过圆上一点作圆的切线的方法.
问题 2 如果直线l是☉O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢
答:由于l是☉O的切线,圆心O到直线l的距离等于半径,所以半径OA是圆心O到直线l的垂线段,即l⊥OA..
【知识归纳】
切线的性质定理:圆的切线垂直于经过切点的半径.
3.例题精讲
例 1 如图,直线AB经过☉O上的点A,且AB=OA,∠OBA=45°.
求证:直线AB是☉O的切线.
证明:∵AB=OA,∠OBA=45°,
∴∠AOB=∠OBA=45°,
∴∠OAB = 90°.
又∵点 A 在圆上,
∴直线AB是☉O的切线.
例 2 如图,在△ABC中,AB=AC,点O在边AB上,☉O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为点F.求证:直线EF是☉O的切线.
证明:连结OE,∵AB=AC,OB=OE,
∴∠B=∠C,∠B=∠OEB,∴∠C=∠OEB,
∴OE∥AC,∴∠OEF=∠EFC.
∵EF⊥AC,∠EFC=90°,∴∠OEF=90°,
∴OE⊥EF.∴EF是☉O的切线.
4.巩固练习 完成教材课后同步练习
5.课堂小结与反思
小结:1.用圆的切线时,常常连结圆心和切点证明切线垂直于半径.
2.“连半径,证垂直”与“作垂直,证半径”是判定直线与圆相切
常用的两种方法.
反思:经历探究切线的判定定理和性质定理的过程,掌握切线的基础知识和基本技能,并能解决简单的问题.
