沪科版数学九年级上册 21.4 二次函数的应用(第2课时)课件(共15张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 21.4 二次函数的应用(第2课时)课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-29 10:49:51 | ||
图片预览




文档简介
(共15张PPT)
第2课时 二次函数的应用(2)
问题:解决生活中面积的实际问题时,你会用到什么知识?所用知识在解决生活中问题时,还应注意哪些问题?
问题导入
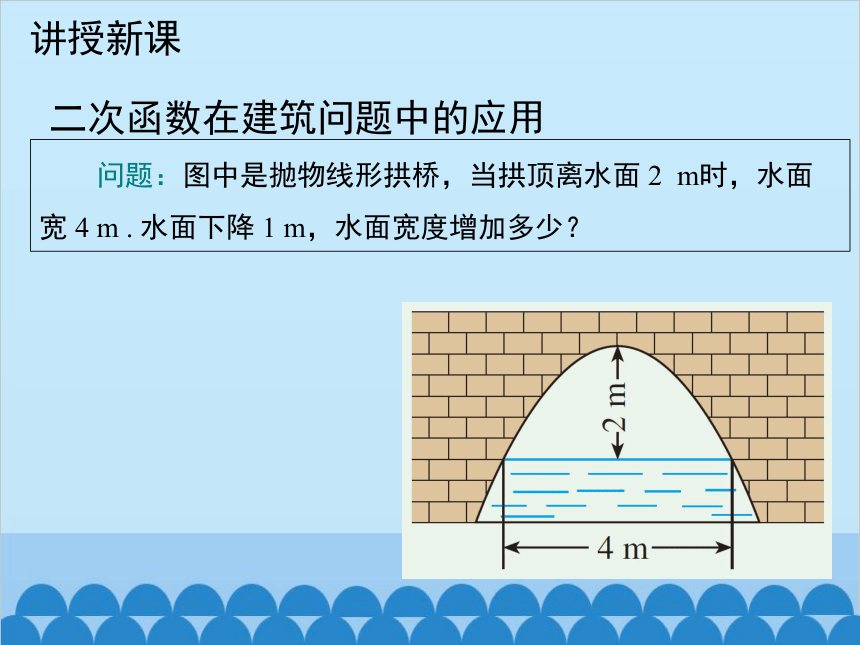
问题:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
讲授新课
二次函数在建筑问题中的应用
(1)求宽度增加多少需要什么数据?
(2)表示水面宽的线段的端点在哪条曲线上?
(3)如何求这组数据?需要先求什么?
(4)图中还知道什么?
(5)怎样求抛物线对应的函数的解析式?
“拱桥”问题
问题探索
问题:如何建立直角坐标系?
l
问题:解决本题的关键是什么?
y
x
o
解:如图建立直角坐标系.
解:建立合适的直角坐标系.
l
y
x
o
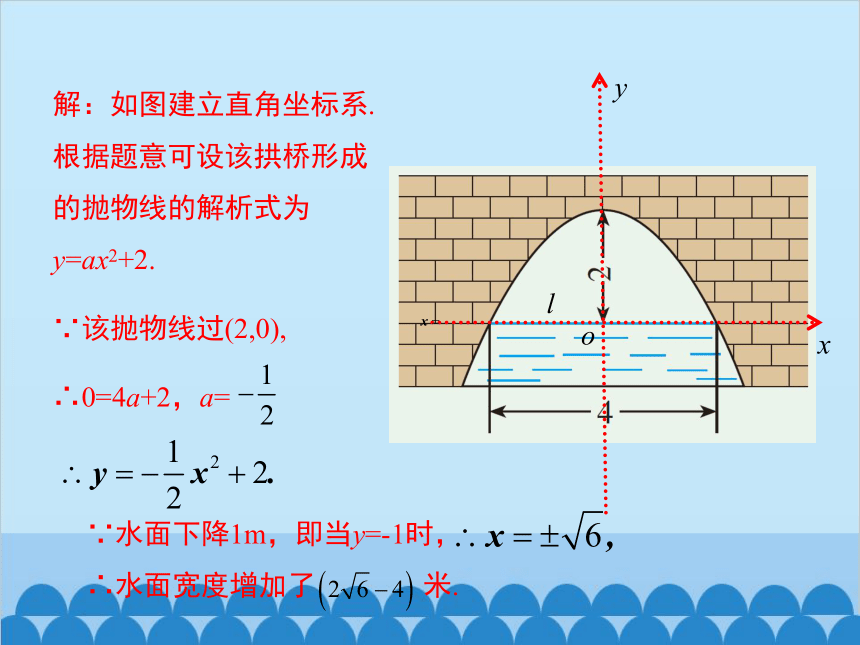
解:如图建立直角坐标系.根据题意可设该拱桥形成的抛物线的解析式为y=ax2+2.
∵该抛物线过(2,0),
∴0=4a+2,a=
∵水面下降1m,即当y=-1时,
∴水面宽度增加了 米.
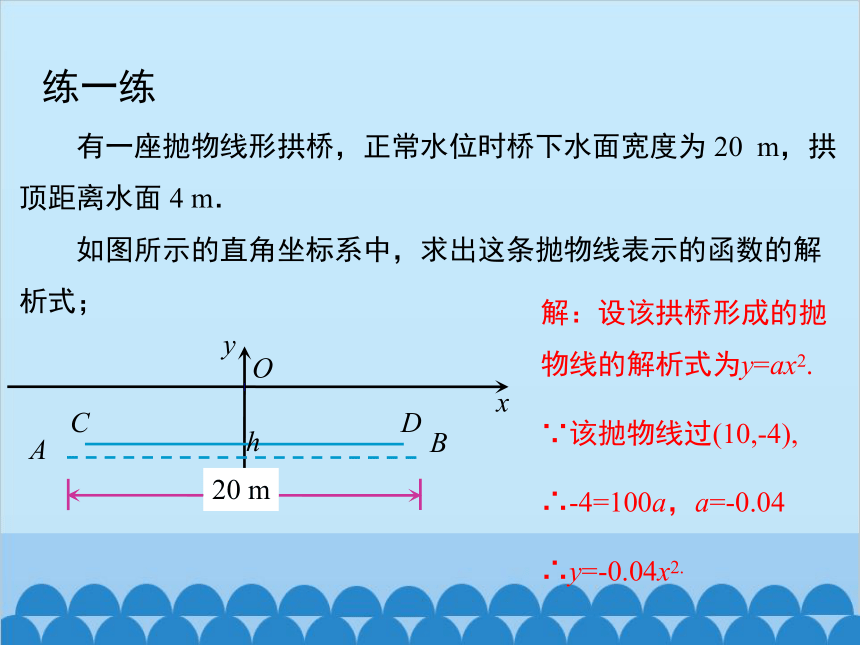
有一座抛物线形拱桥,正常水位时桥下水面宽度为 20 m,拱顶距离水面 4 m.
如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20 m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
练一练
2.根据建立好的坐标系求出该函数的解析式;
3.在实际问题中要注意自变量的取值范围内.
1.用二次函数解决实际问题,首先要建立好模型,而且所建
的坐标系要是最合适的,不然事倍功半;
总结归纳
例:一公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
典例精讲
解:建立如图所示的坐标系,根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
x
y
o
A
●B(1,2.25)
(0,1.25)
●
C(2.5,0)
●
D(-2.5,0)
根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0) ;
同理,点 D的坐标为(-2.5,0) .
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=- (x-1)2+2.25.
1.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
课堂练习
C
2.如图,济南建邦大桥有一段抛物线形的拱梁,抛物线的表达式为y= ax +bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需_____秒.
36
建立二次函数模型解决实际问题的一般步骤:
(1)根据题意建立适当的平面直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析,判断并进行有关的计算.
课堂小结
第2课时 二次函数的应用(2)
问题:解决生活中面积的实际问题时,你会用到什么知识?所用知识在解决生活中问题时,还应注意哪些问题?
问题导入
问题:图中是抛物线形拱桥,当拱顶离水面 2 m时,水面宽 4 m . 水面下降 1 m,水面宽度增加多少?
讲授新课
二次函数在建筑问题中的应用
(1)求宽度增加多少需要什么数据?
(2)表示水面宽的线段的端点在哪条曲线上?
(3)如何求这组数据?需要先求什么?
(4)图中还知道什么?
(5)怎样求抛物线对应的函数的解析式?
“拱桥”问题
问题探索
问题:如何建立直角坐标系?
l
问题:解决本题的关键是什么?
y
x
o
解:如图建立直角坐标系.
解:建立合适的直角坐标系.
l
y
x
o
解:如图建立直角坐标系.根据题意可设该拱桥形成的抛物线的解析式为y=ax2+2.
∵该抛物线过(2,0),
∴0=4a+2,a=
∵水面下降1m,即当y=-1时,
∴水面宽度增加了 米.
有一座抛物线形拱桥,正常水位时桥下水面宽度为 20 m,拱顶距离水面 4 m.
如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20 m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
练一练
2.根据建立好的坐标系求出该函数的解析式;
3.在实际问题中要注意自变量的取值范围内.
1.用二次函数解决实际问题,首先要建立好模型,而且所建
的坐标系要是最合适的,不然事倍功半;
总结归纳
例:一公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
典例精讲
解:建立如图所示的坐标系,根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
x
y
o
A
●B(1,2.25)
(0,1.25)
●
C(2.5,0)
●
D(-2.5,0)
根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0) ;
同理,点 D的坐标为(-2.5,0) .
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=- (x-1)2+2.25.
1.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
课堂练习
C
2.如图,济南建邦大桥有一段抛物线形的拱梁,抛物线的表达式为y= ax +bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需_____秒.
36
建立二次函数模型解决实际问题的一般步骤:
(1)根据题意建立适当的平面直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析,判断并进行有关的计算.
课堂小结
