角平分线的性质
图片预览
文档简介
136导学案——八年级数学(上)
编号: 班级: 姓名:
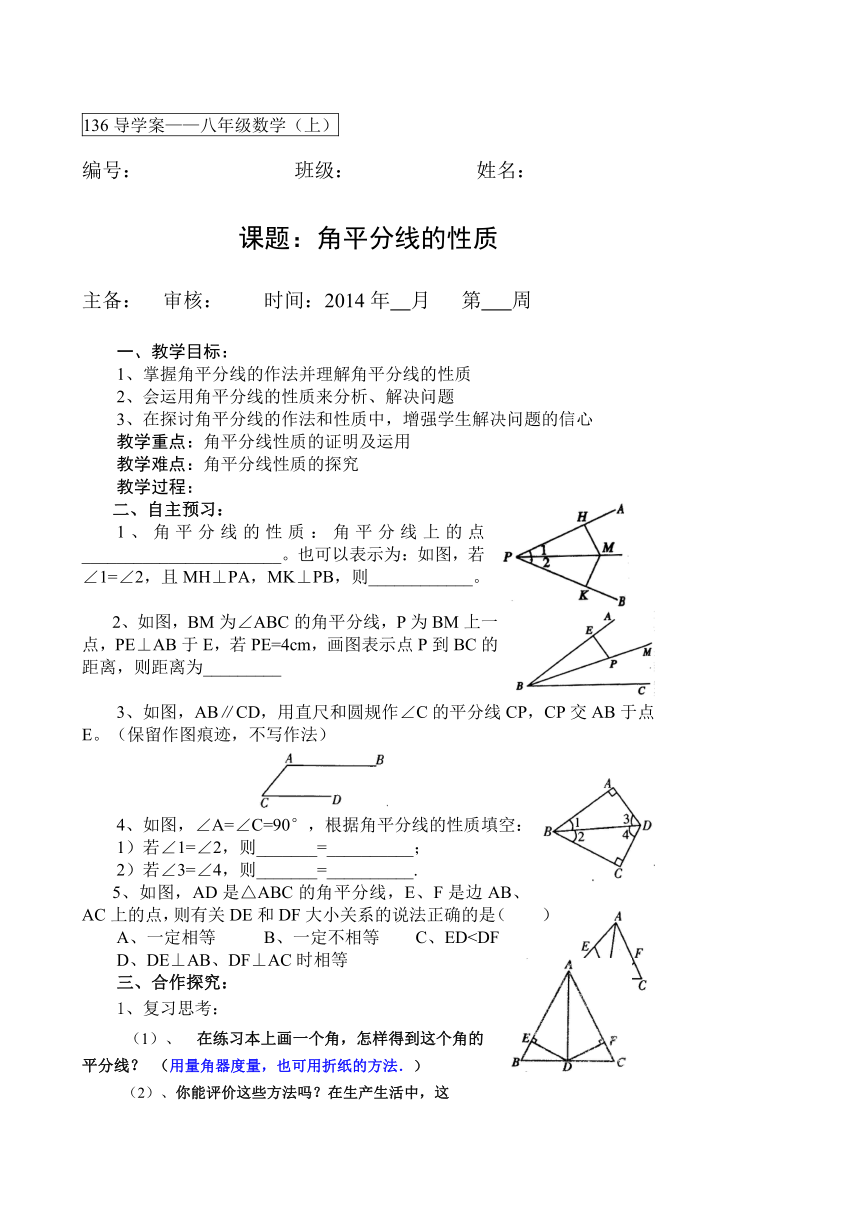
课题:角平分线的性质
主备: 审核: 时间:2014年 月 第 周
一、教学目标:
1、掌握角平分线的作法并理解角平分线的性质
2、会运用角平分线的性质来分析、解决问题
3、在探讨角平分线的作法和性质中,增强学生解决问题的信心
教学重点:角平分线性质的证明及运用
教学难点:角平分线性质的探究
教学过程:
二、自主预习:
1、角平分线的性质:角平分线上的点___ ( http: / / www.21cnjy.com )____________________。也可以表示为:如图,若∠1=∠2,且MH⊥PA,MK⊥PB,则____________。
2、如图,BM为∠ABC的角平分线,P为BM上一点,PE⊥AB于E,若PE=4cm,画图表示点P到BC的距离,则距离为_________
3、如图,AB∥CD,用直尺和圆规作∠C的平分线CP,CP交AB于点E。(保留作图痕迹,不写作法)
4、如图,∠A=∠C=90°,根据角平分线的性质填空:
1)若∠1=∠2,则_______=__________;
2)若∠3=∠4,则_______=__________.
5、如图,AD是△ABC的角平分线,E、F是边AB、AC上的点,则有关DE和DF大小关系的说法正确的是( )
A、一定相等 B、一定不相等 C、EDD、DE⊥AB、DF⊥AC时相等
三、合作探究:
复习思考:
(1)、 在练习本上画一个角,怎样得到这个角的
平分线? (用量角器度量,也可用折纸的方法.)
(2)、你能评价这些方法吗?在生产生活中,这
些方法是否可行呢?
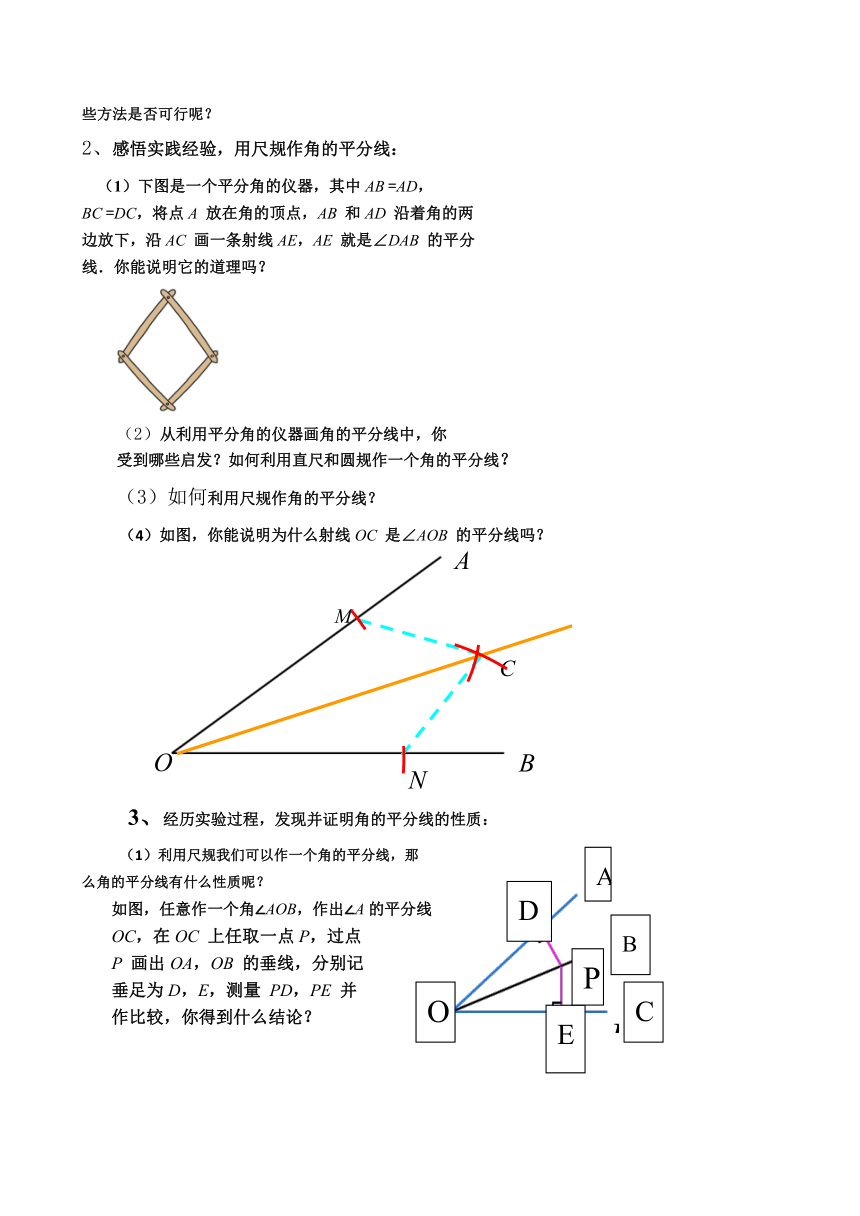
2、感悟实践经验,用尺规作角的平分线:
(1)下图是一个平分角的仪器,其中AB =AD,
BC =DC,将点A 放在角的顶点,AB 和AD 沿着角的两
边放下,沿AC 画一条射线AE,AE 就是∠DAB 的平分
线.你能说明它的道理吗?
( http: / / www.21cnjy.com )
(2)从利用平分角的仪器画角的平分线中,你
受到哪些启发?如何利用直尺和圆规作一个角的平分线?
(3)如何利用尺规作角的平分线?
(4)如图,你能说明为什么射线OC 是∠AOB 的平分线吗?
3、经历实验过程,发现并证明角的平分线的性质:
(1)利用尺规我们可以作一个角的平分线,那
么角的平分线有什么性质呢?
如图,任意作一个角∠AOB,作出∠A的平分线
OC,在OC 上任取一点P,过点
P 画出OA,OB 的垂线,分别记
垂足为D,E,测量 PD,PE 并
作比较,你得到什么结论?
(2) 通过动手实验、观察比较,我们发现“角
的平分线上的点到角的两边的距离相等”,你能通过严
格的逻辑推理证明这个结论吗?(师生共同完成)
(3) 由角的平分线的性质的证明过程,你能概
括出证明几何命题的一般步骤吗?
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出求证的途径,写出证明过程.
(4)角的平分线的性质的作用是什么?
[主要是用于判断和证明两条线段相等,与以前的方
法相比,运用此性质不需要先证两个三角形全等]
四、当堂评价:
1、如图,在△ABC中,AB=AC,AD为 ( http: / / www.21cnjy.com )△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则下列结论①DE=DF;②AD上任意一点到AB、AC的距离相等;③AD平分∠EDF;④∠BDE=∠CDF;⑤BD=CD;⑥AD⊥BC,其中正确的是______(填序号)
2、如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=30cm2,AB=18cm,BC=12cm,则DE=________.
3、如图,在△ABC中,∠B、∠C的平分线交于O,OD⊥AB于D,OE⊥AC于E,则OD与OE的大小关系是( )
A、OD > OE B、OD=OE
C、OD < OE D、不能确定
4、如图,四边形ABCD中,E是AC上一点,ED⊥CD,EB⊥BC,CA平分∠BCD,求证:AD=AB.
( http: / / www.21cnjy.com )
五、拓展提升:
1、如图,BD平分∠ABC,∠DAB+∠DCB=180°,求证:AD=CD.
( http: / / www.21cnjy.com )
2、如图,在△ABC中,∠A=60°,△ABC的角平分线BD、CE交于点O,且OB=OC,求证:BE+CD=BC.
( http: / / www.21cnjy.com )
六、课后检测:
1、如图,Q是△OAB的角平分线OP上的一 ( http: / / www.21cnjy.com )点,PC⊥OA于C,PD⊥OB于D,QE⊥OB于E,FQ⊥OP交OA于F,则下列结论正确的是( )
A、PA=PB B、PC=PD C、QE=OF D、PC=QE
2、如图,已知AB∥CD,O是∠ACD、∠CAB的角平分线的交点,且OE⊥AC于E,OE=12,则AB与CD之间的距离为________.
3、在Rt△ABC中,∠C=90°,∠A的平分线与∠B的平分线交于点D,∠ADB=__________°
4、△ABC中,∠C=90°,AD平分∠BAC交BC于D,若DC=7,则D到AB的距离是________.
5、如图所示,在△ABC中,AD是角平分线,DE⊥AB于E,DF⊥AC于F,求证:1)AE=AF;2)DA平分∠EDF.
( http: / / www.21cnjy.com )
6、如图,在四边形ABCD中,AC平分∠BAD,过点C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE=(AB+AD)
( http: / / www.21cnjy.com )
七、课堂小结:这堂课学到了什么?(学生总结)
八、教学反思:
A
B
O
M
N
C
A
A
B
O
P
C
D
E
D
B
P
O
C
E
编号: 班级: 姓名:
课题:角平分线的性质
主备: 审核: 时间:2014年 月 第 周
一、教学目标:
1、掌握角平分线的作法并理解角平分线的性质
2、会运用角平分线的性质来分析、解决问题
3、在探讨角平分线的作法和性质中,增强学生解决问题的信心
教学重点:角平分线性质的证明及运用
教学难点:角平分线性质的探究
教学过程:
二、自主预习:
1、角平分线的性质:角平分线上的点___ ( http: / / www.21cnjy.com )____________________。也可以表示为:如图,若∠1=∠2,且MH⊥PA,MK⊥PB,则____________。
2、如图,BM为∠ABC的角平分线,P为BM上一点,PE⊥AB于E,若PE=4cm,画图表示点P到BC的距离,则距离为_________
3、如图,AB∥CD,用直尺和圆规作∠C的平分线CP,CP交AB于点E。(保留作图痕迹,不写作法)
4、如图,∠A=∠C=90°,根据角平分线的性质填空:
1)若∠1=∠2,则_______=__________;
2)若∠3=∠4,则_______=__________.
5、如图,AD是△ABC的角平分线,E、F是边AB、AC上的点,则有关DE和DF大小关系的说法正确的是( )
A、一定相等 B、一定不相等 C、ED
三、合作探究:
复习思考:
(1)、 在练习本上画一个角,怎样得到这个角的
平分线? (用量角器度量,也可用折纸的方法.)
(2)、你能评价这些方法吗?在生产生活中,这
些方法是否可行呢?
2、感悟实践经验,用尺规作角的平分线:
(1)下图是一个平分角的仪器,其中AB =AD,
BC =DC,将点A 放在角的顶点,AB 和AD 沿着角的两
边放下,沿AC 画一条射线AE,AE 就是∠DAB 的平分
线.你能说明它的道理吗?
( http: / / www.21cnjy.com )
(2)从利用平分角的仪器画角的平分线中,你
受到哪些启发?如何利用直尺和圆规作一个角的平分线?
(3)如何利用尺规作角的平分线?
(4)如图,你能说明为什么射线OC 是∠AOB 的平分线吗?
3、经历实验过程,发现并证明角的平分线的性质:
(1)利用尺规我们可以作一个角的平分线,那
么角的平分线有什么性质呢?
如图,任意作一个角∠AOB,作出∠A的平分线
OC,在OC 上任取一点P,过点
P 画出OA,OB 的垂线,分别记
垂足为D,E,测量 PD,PE 并
作比较,你得到什么结论?
(2) 通过动手实验、观察比较,我们发现“角
的平分线上的点到角的两边的距离相等”,你能通过严
格的逻辑推理证明这个结论吗?(师生共同完成)
(3) 由角的平分线的性质的证明过程,你能概
括出证明几何命题的一般步骤吗?
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出求证的途径,写出证明过程.
(4)角的平分线的性质的作用是什么?
[主要是用于判断和证明两条线段相等,与以前的方
法相比,运用此性质不需要先证两个三角形全等]
四、当堂评价:
1、如图,在△ABC中,AB=AC,AD为 ( http: / / www.21cnjy.com )△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则下列结论①DE=DF;②AD上任意一点到AB、AC的距离相等;③AD平分∠EDF;④∠BDE=∠CDF;⑤BD=CD;⑥AD⊥BC,其中正确的是______(填序号)
2、如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=30cm2,AB=18cm,BC=12cm,则DE=________.
3、如图,在△ABC中,∠B、∠C的平分线交于O,OD⊥AB于D,OE⊥AC于E,则OD与OE的大小关系是( )
A、OD > OE B、OD=OE
C、OD < OE D、不能确定
4、如图,四边形ABCD中,E是AC上一点,ED⊥CD,EB⊥BC,CA平分∠BCD,求证:AD=AB.
( http: / / www.21cnjy.com )
五、拓展提升:
1、如图,BD平分∠ABC,∠DAB+∠DCB=180°,求证:AD=CD.
( http: / / www.21cnjy.com )
2、如图,在△ABC中,∠A=60°,△ABC的角平分线BD、CE交于点O,且OB=OC,求证:BE+CD=BC.
( http: / / www.21cnjy.com )
六、课后检测:
1、如图,Q是△OAB的角平分线OP上的一 ( http: / / www.21cnjy.com )点,PC⊥OA于C,PD⊥OB于D,QE⊥OB于E,FQ⊥OP交OA于F,则下列结论正确的是( )
A、PA=PB B、PC=PD C、QE=OF D、PC=QE
2、如图,已知AB∥CD,O是∠ACD、∠CAB的角平分线的交点,且OE⊥AC于E,OE=12,则AB与CD之间的距离为________.
3、在Rt△ABC中,∠C=90°,∠A的平分线与∠B的平分线交于点D,∠ADB=__________°
4、△ABC中,∠C=90°,AD平分∠BAC交BC于D,若DC=7,则D到AB的距离是________.
5、如图所示,在△ABC中,AD是角平分线,DE⊥AB于E,DF⊥AC于F,求证:1)AE=AF;2)DA平分∠EDF.
( http: / / www.21cnjy.com )
6、如图,在四边形ABCD中,AC平分∠BAD,过点C作CE⊥AB于E,且CD=CB,∠ABC+∠ADC=180°.求证:AE=(AB+AD)
( http: / / www.21cnjy.com )
七、课堂小结:这堂课学到了什么?(学生总结)
八、教学反思:
A
B
O
M
N
C
A
A
B
O
P
C
D
E
D
B
P
O
C
E
