华师版数学七年级上册 2.2.1数轴(2)课件(共16张PPT)
文档属性
| 名称 | 华师版数学七年级上册 2.2.1数轴(2)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 418.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-29 14:41:56 | ||
图片预览




文档简介
(共16张PPT)
2.2 数轴
第1课时 数轴
学习目标
通过实例了解数轴的概念、三要素和数轴的画法.
理解数轴上的点和有理数的对应关系,能读出数轴上的数,会画数轴,并能在数轴上表示有理数.
通过数轴的学习和应用,接触数形结合的思想方法.
1
3
2
温故知新
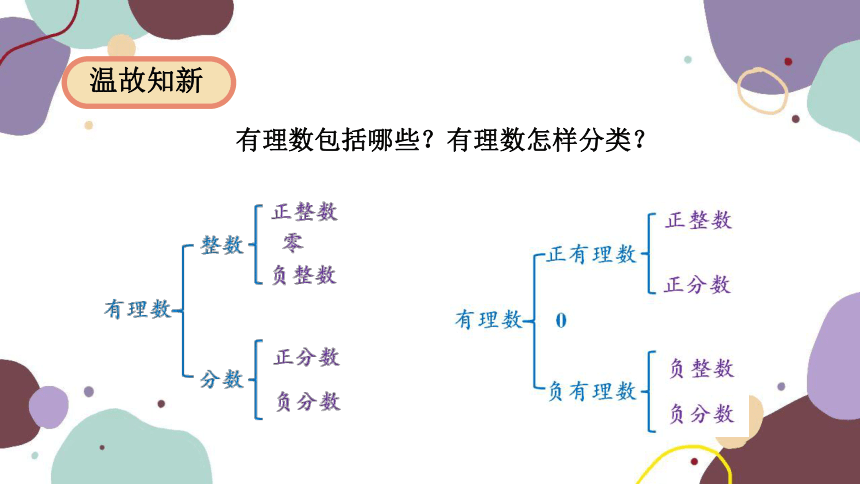
有理数包括哪些?有理数怎样分类?
观察右侧的温度计,我们把它“放平”,温度计上的刻度有什么特点?
每个刻度代表一个数,有正数,0,负数.
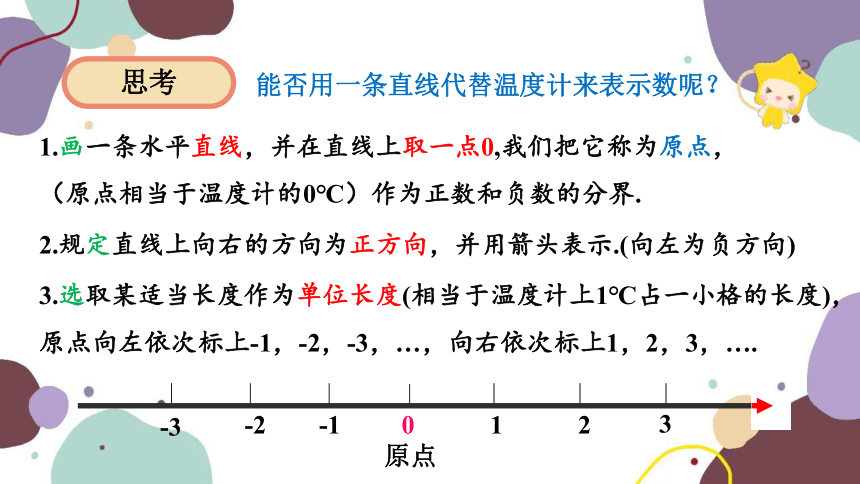
能否用一条直线代替温度计来表示数呢?
1.画一条水平直线,并在直线上取一点0,我们把它称为原点,
(原点相当于温度计的0℃)作为正数和负数的分界.
2.规定直线上向右的方向为正方向,并用箭头表示.(向左为负方向)
3.选取某适当长度作为单位长度(相当于温度计上1℃占一小格的长度),原点向左依次标上-1,-2,-3,…,向右依次标上1,2,3,….
0
原点
1
2
3
-1
-2
-3
思考
如何画数轴?
新知讲解
概括
像这样规定了原点、正方向和单位长度的直线叫做数轴.
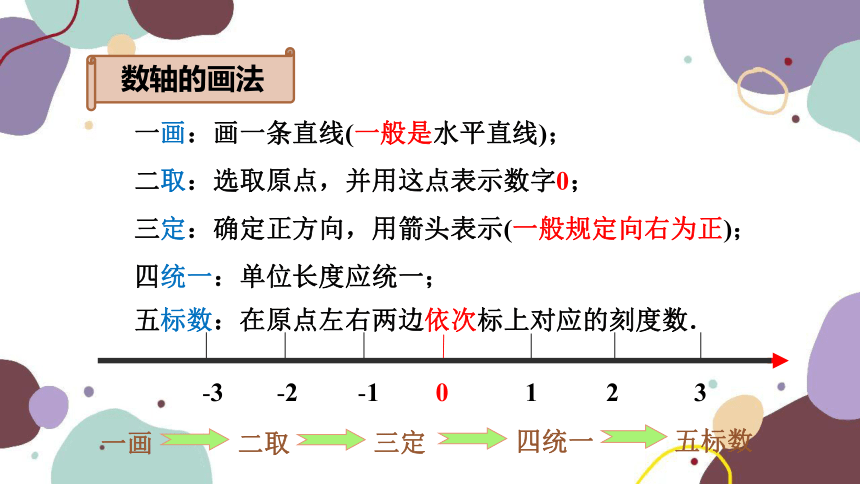
数轴的画法
0
1
2
3
-1
-2
-3
一画:画一条直线(一般是水平直线);
二取:选取原点,并用这点表示数字0;
三定:确定正方向,用箭头表示(一般规定向右为正);
四统一:单位长度应统一;
五标数:在原点左右两边依次标上对应的刻度数.
一画
二取
三定
四统一
五标数
0
1
2
3
-1
-2
-3
观察下面的数轴,思考:怎样判断数轴的对错?
数轴三要素
数轴三要素:
原点;
正方向;
单位长度.
例题
例1.判断下列所画数轴是否正确,并说明理由.
1
2
-1
-2
(1)
(2)
0
(3)
(4)
1
2
0
-1
1
2
0
-1
(5)
(6)
-1
-2
0
1
1
2
0
-1
1
2
0
-1
(7)
(8)
100
200
0
-100
没有原点
没有单位长度
没有正方向
正方向标识错误
标数错误
单位长度不一致
×
×
×
×
×
×
√
√
0
1
2
3
-1
-2
-3
观察下面的数轴,思考:两个绿色的点表示什么数?
到原点的距离是多少?
右边绿点表示+ 3 , 它到原点的距离是3 个单位长度;
左边绿点表示- 3 , 它到原点的距离是3 个单位长度.
数轴上的点的绝对值表示该点到原点的距离.
思考
例题
0
1
2
3
-1
-2
-3
-4
-5
4
任何一个有理数都可以用数轴上的一个点来表示.
解:如图所示.
-4.5
-2
0
4
变式训练
解:点A表示 -2;
点B表示2;
点C表示0;
点D表示-1.
指出数轴上A,B,C,D各点分别表示什么数.
0
1
2
3
-1
-2
-3
A
B
C
D
数轴上表示有理数的点都表示唯一一个有理数.
数轴上的点与有理数是一一对应的.
1.下列说法正确的是( )
A.数轴是一条带箭头的射线
B. 数轴一定取向右为正方向
C. 数轴是一条规定了原点、单位长度和正方向的直线
D. 数轴上的原点表示有理数的起点
C
练习
2.下列语句中正确的是( )
数轴上的点只能表示整数
B. 在数轴上-2与2之间的有理数只有4个
C. 数轴上的一个点只能表示一个数
D. 一个有理数可以用同一数轴上不同的几个点来表示
C
练习
3.一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-3;如果点A表示数-1,将点A向右移动4个单位长度,那么终点B表示的数是______,此时A,B两点相距________个单位长度.
-4 -3 -2 -1 0 1 2 3
2
5
3
4
练习
1.数轴的定义:规定了原点 、 正方向和单位长度的直线叫做数轴 ;
2.数轴的三要素:原点,正方向,单位长度;
3.数轴上的点与有理数是一一对应的.
总结
2.2 数轴
第1课时 数轴
学习目标
通过实例了解数轴的概念、三要素和数轴的画法.
理解数轴上的点和有理数的对应关系,能读出数轴上的数,会画数轴,并能在数轴上表示有理数.
通过数轴的学习和应用,接触数形结合的思想方法.
1
3
2
温故知新
有理数包括哪些?有理数怎样分类?
观察右侧的温度计,我们把它“放平”,温度计上的刻度有什么特点?
每个刻度代表一个数,有正数,0,负数.
能否用一条直线代替温度计来表示数呢?
1.画一条水平直线,并在直线上取一点0,我们把它称为原点,
(原点相当于温度计的0℃)作为正数和负数的分界.
2.规定直线上向右的方向为正方向,并用箭头表示.(向左为负方向)
3.选取某适当长度作为单位长度(相当于温度计上1℃占一小格的长度),原点向左依次标上-1,-2,-3,…,向右依次标上1,2,3,….
0
原点
1
2
3
-1
-2
-3
思考
如何画数轴?
新知讲解
概括
像这样规定了原点、正方向和单位长度的直线叫做数轴.
数轴的画法
0
1
2
3
-1
-2
-3
一画:画一条直线(一般是水平直线);
二取:选取原点,并用这点表示数字0;
三定:确定正方向,用箭头表示(一般规定向右为正);
四统一:单位长度应统一;
五标数:在原点左右两边依次标上对应的刻度数.
一画
二取
三定
四统一
五标数
0
1
2
3
-1
-2
-3
观察下面的数轴,思考:怎样判断数轴的对错?
数轴三要素
数轴三要素:
原点;
正方向;
单位长度.
例题
例1.判断下列所画数轴是否正确,并说明理由.
1
2
-1
-2
(1)
(2)
0
(3)
(4)
1
2
0
-1
1
2
0
-1
(5)
(6)
-1
-2
0
1
1
2
0
-1
1
2
0
-1
(7)
(8)
100
200
0
-100
没有原点
没有单位长度
没有正方向
正方向标识错误
标数错误
单位长度不一致
×
×
×
×
×
×
√
√
0
1
2
3
-1
-2
-3
观察下面的数轴,思考:两个绿色的点表示什么数?
到原点的距离是多少?
右边绿点表示+ 3 , 它到原点的距离是3 个单位长度;
左边绿点表示- 3 , 它到原点的距离是3 个单位长度.
数轴上的点的绝对值表示该点到原点的距离.
思考
例题
0
1
2
3
-1
-2
-3
-4
-5
4
任何一个有理数都可以用数轴上的一个点来表示.
解:如图所示.
-4.5
-2
0
4
变式训练
解:点A表示 -2;
点B表示2;
点C表示0;
点D表示-1.
指出数轴上A,B,C,D各点分别表示什么数.
0
1
2
3
-1
-2
-3
A
B
C
D
数轴上表示有理数的点都表示唯一一个有理数.
数轴上的点与有理数是一一对应的.
1.下列说法正确的是( )
A.数轴是一条带箭头的射线
B. 数轴一定取向右为正方向
C. 数轴是一条规定了原点、单位长度和正方向的直线
D. 数轴上的原点表示有理数的起点
C
练习
2.下列语句中正确的是( )
数轴上的点只能表示整数
B. 在数轴上-2与2之间的有理数只有4个
C. 数轴上的一个点只能表示一个数
D. 一个有理数可以用同一数轴上不同的几个点来表示
C
练习
3.一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-3;如果点A表示数-1,将点A向右移动4个单位长度,那么终点B表示的数是______,此时A,B两点相距________个单位长度.
-4 -3 -2 -1 0 1 2 3
2
5
3
4
练习
1.数轴的定义:规定了原点 、 正方向和单位长度的直线叫做数轴 ;
2.数轴的三要素:原点,正方向,单位长度;
3.数轴上的点与有理数是一一对应的.
总结
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
