2023年广东省深圳市宝安区中考数学备考冲刺题--模拟卷1(参考答案与评分标准)
文档属性
| 名称 | 2023年广东省深圳市宝安区中考数学备考冲刺题--模拟卷1(参考答案与评分标准) |  | |
| 格式 | docx | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-29 08:56:16 | ||
图片预览


文档简介
2023年广东省深圳市宝安区中考数学备考冲刺题--模拟卷1
参考答案与评分标准
第一部分 选择题
一、选择题(本大题共10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C C B A C D D B
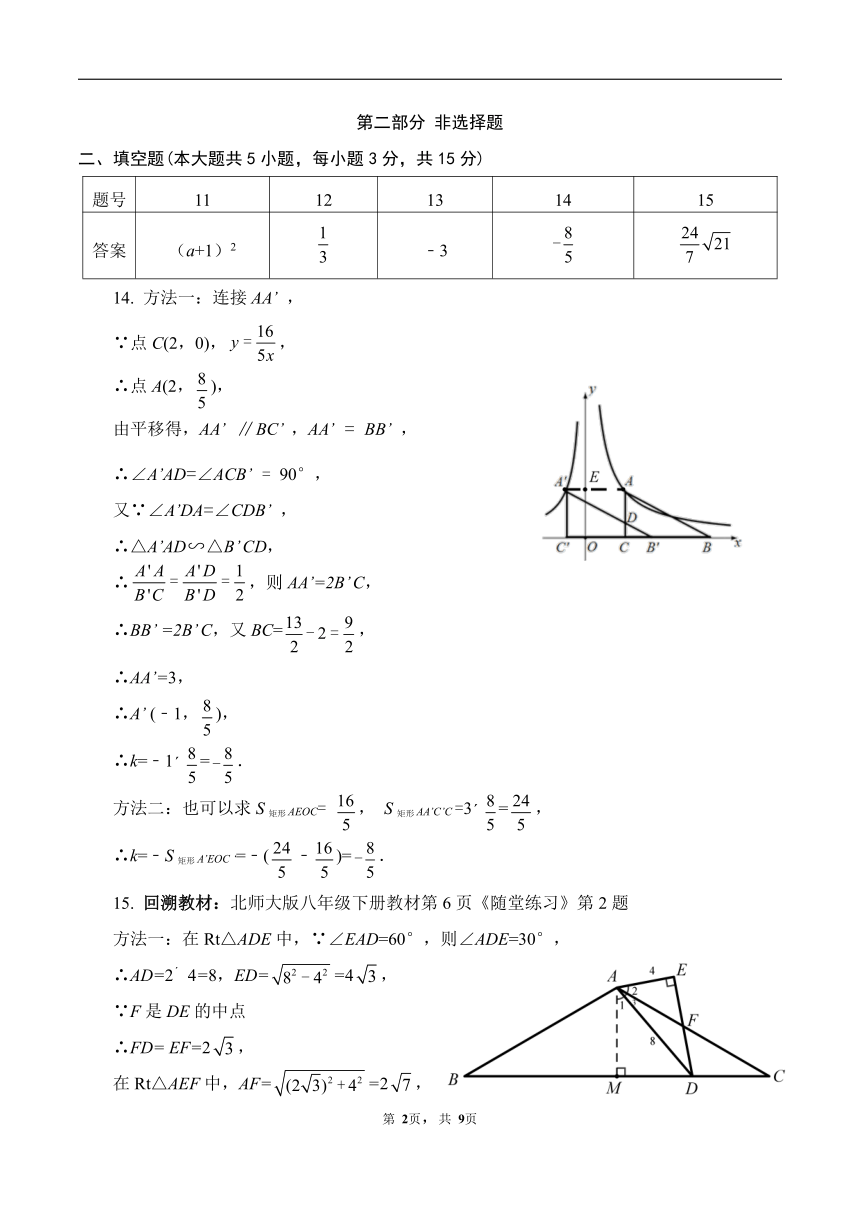
10.回溯教材:北师大版九年级下册教材第73页《习题3.2》第3题
方法一:如图1,∵OC=OA,
∴∠1=∠3(等边对等角),
∵OC∥AD,
∴∠2=∠3(两直线平行内错角相等),
∴∠1=∠2,
∵∠1=∠2,
过点C作CF ┴ AF交AF的延长线于F,
∵∠1=∠2,CF ┴ AF ,CE ┴ AB, 图1
∴CF=CE(角平分线上的点到角两边的距离相等) ,
∵∠F=∠CEB=90°,CF=CE,AC= AC,
∴△ACF≌△ACE(HL),
∴S△ACF = S△ACE,
∵∠ADC+∠FDC=180°,∠ADC+∠B=180°
(圆内接四边形的对角互补),
∴∠B=∠FDC,
又∵∠F=∠CEB=90°,CF=CE,
∴△CDF≌△CBE(AAS),
∴S△CDF = S△CBE, 图2
∵S四边形ABCD = S△CBE + S四边形AOCD = S△CDF + S四边形AOCD= S四边形AECF =2S△ACF,
∴△ACE和和四边形ABCD的面积之比为1:2.
方法二:如图1,也可以用∠1=∠2,推导CD=BC,证得△CDF≌△CBE(HL).
方法三:如图2,也可以用教材中的方法,连接OD,证得
CO平分∠BOD,从而CD=BC .
第二部分 非选择题
二、填空题(本大题共5小题,每小题3分,共15分)
题号 11 12 13 14 15
答案 (a+1)2 ﹣3
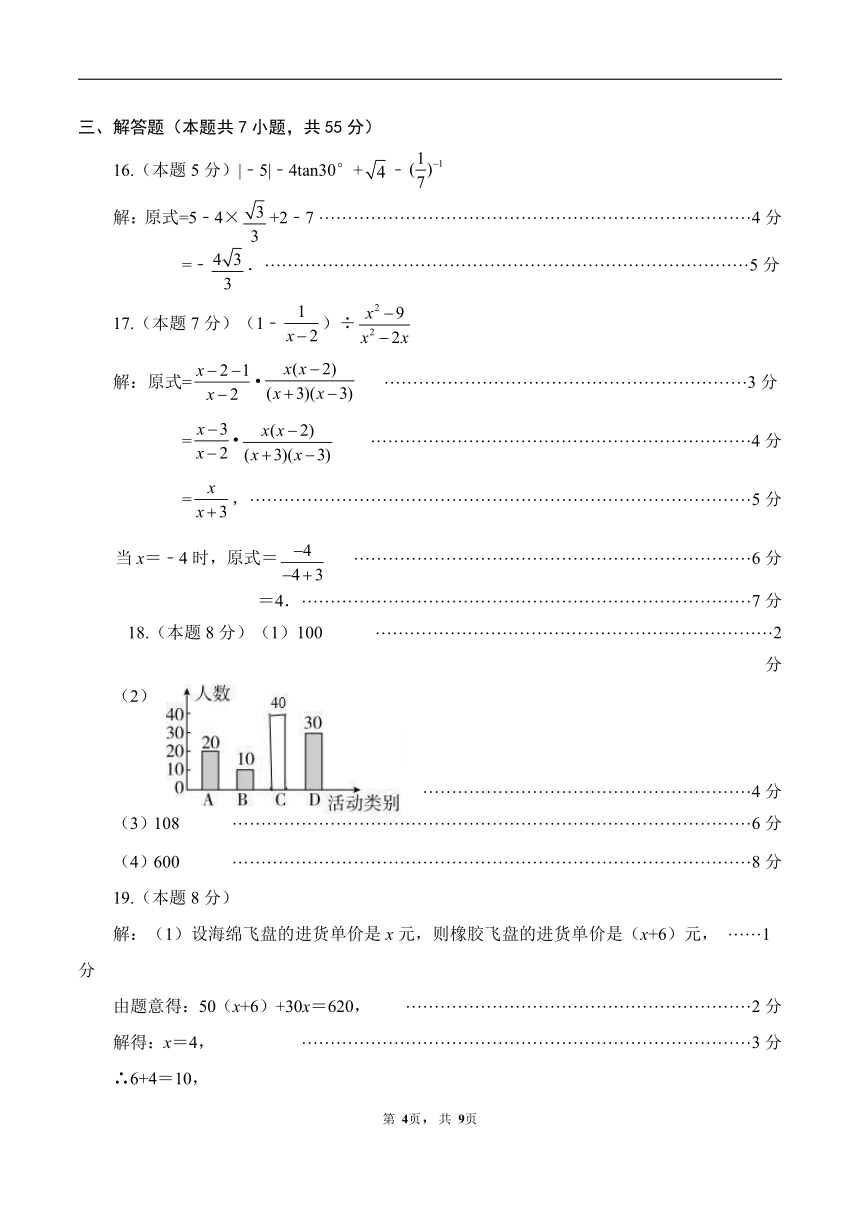
14. 方法一:连接AA’ ,
∵点C(2,0),,
∴点A(2,),
由平移得,AA’ ∥BC’ ,AA’ = BB’ ,
∴∠A’AD=∠ACB’ = 90°,
又∵∠A’DA=∠CDB’ ,
∴△A’AD∽△B’ CD,
∴,则AA’=2B’ C,
∴BB’ =2B’ C,又BC=,
∴AA’=3,
∴A’ (﹣1,),
∴k=﹣1=.
方法二:也可以求S矩形AEOC= , S矩形AA’C’C =3=,
∴k=﹣S矩形A’EOC ‘=﹣(﹣)=.
15. 回溯教材:北师大版八年级下册教材第6页《随堂练习》第2题
方法一:在Rt△ADE中,∵∠EAD=60°,则∠ADE=30°,
∴AD=24=8,ED==4,
∵F是DE的中点
∴FD= EF=2,
在Rt△AEF中,AF==2,
过点A作AM┴BC,
∵AB=AC,AM┴BC,
∴∠MAC=∠ABM=60°,
∵∠1+∠3=60°,∠2+∠3=60°,
∴∠1=∠2,
又∵∠AMD=∠E=90°,
∴△AMD∽△AEF,
∴,则AM=,DM=,
在Rt△AEF中,AF==,
∴BD=+=.
方法二:如图1,也可以用△AFD∽△ADC,推得AD2= AF AC ,则AC=,
CF=﹣2=.
再用△ABD∽△DCF ,推得,
BD=.
方法三:如图2,也可以用△AFD∽△ADC,推得AD2= AF AC ,则AC=,
BC=.然后再次利用△AFD∽△ADC,推得CD=,则BD=.
图1 图2
三、解答题(本题共7小题,共55分)
16.(本题5分)|﹣5|﹣4tan30°+﹣
解:原式=5﹣4×+2﹣7 …………………………………………………………………4分
=﹣.…………………………………………………………………………5分
17.(本题7分)(1﹣)÷
解:原式= ………………………………………………………3分
= …………………………………………………………4分
=,……………………………………………………………………………5分
当x=﹣4时,原式= ……………………………………………………………6分
=4.……………………………………………………………………7分
18.(本题8分)(1)100 ……………………………………………………………2分
(2)
…………………………………………………4分
(3)108 ………………………………………………………………………………6分
(4)600 ………………………………………………………………………………8分
19.(本题8分)
解:(1)设海绵飞盘的进货单价是x元,则橡胶飞盘的进货单价是(x+6)元, ……1分
由题意得:50(x+6)+30x=620, ……………………………………………………2分
解得:x=4, ……………………………………………………………………3分
∴6+4=10,
答:海绵飞盘的进货单价是4元,则橡胶飞盘的进货单价是10元 …………………4分
(备注:列二元一次方程组也可以);
(2)设第二批购进橡胶飞盘y个,则海绵飞盘购进(300﹣y)个,获得利润为w元,
∵y≤2(300﹣y),
∴0<y≤200, ……………………………………………………………………5分
由题意得:w=(14﹣10)y+(6﹣4)(300﹣y)=2y+600, ……………………6分
∵2>0,
∴w随y的增大而增大, ……………………………………………………………7分
∴当y=200时,w有最大值,w最大值=400+600=1000,
答:第二批购进橡胶飞盘200个时,总利润最大,最大利润是1000元. …………8分
20.(本题8分)回溯教材:北师大版九年级下册教材第41页《习题2.5》第4题
(1)13 59.9 ………………………………………………2分
(2)
(备注:描点1分,连线1分) ……………………………………………4分
(3)增强 降低 ………………………………………………………………6分
(4)当y=59时,﹣0.1x2+2.6x+43=59, …………………………………………7分
解得x1=10,x2=16,
答:某同学对概念的接受能力达到59时,他提出概念所用的时间是10分钟或16分钟.…8分
21.(本题9分)回溯教材:北师大版九年级下册教材第81页《习题3.4》第4题
(1)< < ………………………………………………………………………2分
(2)①∠AQB<∠APB;………………………3分
②记BQ与O相交于点H,连接AH,
∵=
∴∠APB=∠AHB, ………………………4分
∵∠AHB是△AHQ的外角,
∴∠AQB<∠AHB,
∴∠AQB<∠APB. ………………………5分
(3)方法一:由(2)知,过点A、B的圆O与PQ相切时,射门角度(∠AMB)最大,连接AM,AN,延长QP交AB的延长线于点G, …………………………………6分
在Rt△DPG中,∵∠DPG=∠QPC,
∴DG=7.5×=米,
PG=7.5×=米,GB=+15.5=米, …………………………7分
GA=+7=米,
∵∠GMB=∠GAM,
又∵∠G为公共角,
∴△GMB∽△GAM,
∴,
即 GM 2=GBGA,
GM 2=×,解得GM=米, ………………………………………8分
PM=﹣=15米
综上, PM的长度为15米. ………………………………………9分
方法二:由(2)知,过点A、B的圆O与PQ相切时,射门角度(∠AMB)最大,
∴∠OMF=90°, ………………………………………6分
如图,作AB的中垂线EF交AB于点E,交PQ于点F,则点O在线段EF上,
∴BE=7×=3.5米,则DE=3.5+15.5=19米,
过点F作FG ┴ CD于点G,
∴四边形EFGD是矩形,
∴FG=DE=19米,
在Rt△EPG中,PG==米,
sin∠QPC=,PF==米, …………………………………………7分
EF=DG=7.5+=米,
∵EF ∥DG ,
∴∠OFM=∠FPG ,
设圆O的半径为R,在Rt△OFM中,OF==R,
EO=﹣R,
∵OB2=OE2+EB2,
∴R2=(﹣R)2+3.52,解得R=(舍去)或, …………………8分
∴MF=米,
PM=﹣=15米.
综上, PM的长度为15米. …………………………………………………9分
22.(本题10分)回溯教材:北师大版九年级上册教材第25页《习题1.8》第4题
解:(1)∵四边形ABCD是正方形,
∴OC=OD,∠COD=90°,∠BCD=90°,
∴∠ODN=∠OCD=45°,
∴∠OCB=90°﹣45°=45°, …………1分
∵四边形A’B’C’O是正方形,
∴∠A’OC’=90°,
∴∠MOC+∠CO N=90°,
又∵∠NOD +∠CON=90°,
∴∠MOC=∠NOD, …………2分
在△OMC和△OND中,,
∴△OMC≌△OND. …………………………………………………3分
(2)∵四边形ABCD是矩形,
∴BC=AD=12,CD=AB=6,
AC=BD,OC=AD,OB=OD=BD,
∴OB=OC=OD,
过点O分别作OF┴ CD交CD于F, OE┴ BC交BC于点E, 则四边形OECF是矩形,
∴∠EOF=90°,OF=CE,OE=CF,
∵OB=OC, OE┴ BC,
∴CE=×12=6,
∵OD=OC, OF┴ DC,
∴CF=DF=×6=3,则FN=3﹣1=2,
∵四边形A’B’C’O是矩形,
∴∠A’OC’=90°,
∴∠MOF+∠FON=90°,
又∵∠MOF +∠MOE=90°, ……………………………………………4分
∴∠FON=∠MOE,
又∵∠OFN=∠OEM=90°,
∴△OFN∽△OEM, ……………………………………………5分
∴,则EM=1,
∴CM=6﹣1=5. ……………………………………………………6分
(3)或 ………………………………………………………………………10分
(备注:每种情况各2分)
解析:①当∠BDC=90°时,如图1,△ODN∽△OEM,且相似比为:1,
可求得OE=,BE=,
设ME=x,则DN=x,CN=3﹣x,
∵ ABCD与 A’B’C’O重叠部分的面积是 ABCD的面积的,
∴S△OC N = S△OBM,则BM=CN=(3﹣x),
∵(3﹣x)+ x=,
∴x=,则DN=,
在Rt△ODN中,ON=,
图1 图2
②当∠BDC=90°时,如图2,ON是△BCD的中位线,于是ON=.
第 3页,共 9页
参考答案与评分标准
第一部分 选择题
一、选择题(本大题共10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C C B A C D D B
10.回溯教材:北师大版九年级下册教材第73页《习题3.2》第3题
方法一:如图1,∵OC=OA,
∴∠1=∠3(等边对等角),
∵OC∥AD,
∴∠2=∠3(两直线平行内错角相等),
∴∠1=∠2,
∵∠1=∠2,
过点C作CF ┴ AF交AF的延长线于F,
∵∠1=∠2,CF ┴ AF ,CE ┴ AB, 图1
∴CF=CE(角平分线上的点到角两边的距离相等) ,
∵∠F=∠CEB=90°,CF=CE,AC= AC,
∴△ACF≌△ACE(HL),
∴S△ACF = S△ACE,
∵∠ADC+∠FDC=180°,∠ADC+∠B=180°
(圆内接四边形的对角互补),
∴∠B=∠FDC,
又∵∠F=∠CEB=90°,CF=CE,
∴△CDF≌△CBE(AAS),
∴S△CDF = S△CBE, 图2
∵S四边形ABCD = S△CBE + S四边形AOCD = S△CDF + S四边形AOCD= S四边形AECF =2S△ACF,
∴△ACE和和四边形ABCD的面积之比为1:2.
方法二:如图1,也可以用∠1=∠2,推导CD=BC,证得△CDF≌△CBE(HL).
方法三:如图2,也可以用教材中的方法,连接OD,证得
CO平分∠BOD,从而CD=BC .
第二部分 非选择题
二、填空题(本大题共5小题,每小题3分,共15分)
题号 11 12 13 14 15
答案 (a+1)2 ﹣3
14. 方法一:连接AA’ ,
∵点C(2,0),,
∴点A(2,),
由平移得,AA’ ∥BC’ ,AA’ = BB’ ,
∴∠A’AD=∠ACB’ = 90°,
又∵∠A’DA=∠CDB’ ,
∴△A’AD∽△B’ CD,
∴,则AA’=2B’ C,
∴BB’ =2B’ C,又BC=,
∴AA’=3,
∴A’ (﹣1,),
∴k=﹣1=.
方法二:也可以求S矩形AEOC= , S矩形AA’C’C =3=,
∴k=﹣S矩形A’EOC ‘=﹣(﹣)=.
15. 回溯教材:北师大版八年级下册教材第6页《随堂练习》第2题
方法一:在Rt△ADE中,∵∠EAD=60°,则∠ADE=30°,
∴AD=24=8,ED==4,
∵F是DE的中点
∴FD= EF=2,
在Rt△AEF中,AF==2,
过点A作AM┴BC,
∵AB=AC,AM┴BC,
∴∠MAC=∠ABM=60°,
∵∠1+∠3=60°,∠2+∠3=60°,
∴∠1=∠2,
又∵∠AMD=∠E=90°,
∴△AMD∽△AEF,
∴,则AM=,DM=,
在Rt△AEF中,AF==,
∴BD=+=.
方法二:如图1,也可以用△AFD∽△ADC,推得AD2= AF AC ,则AC=,
CF=﹣2=.
再用△ABD∽△DCF ,推得,
BD=.
方法三:如图2,也可以用△AFD∽△ADC,推得AD2= AF AC ,则AC=,
BC=.然后再次利用△AFD∽△ADC,推得CD=,则BD=.
图1 图2
三、解答题(本题共7小题,共55分)
16.(本题5分)|﹣5|﹣4tan30°+﹣
解:原式=5﹣4×+2﹣7 …………………………………………………………………4分
=﹣.…………………………………………………………………………5分
17.(本题7分)(1﹣)÷
解:原式= ………………………………………………………3分
= …………………………………………………………4分
=,……………………………………………………………………………5分
当x=﹣4时,原式= ……………………………………………………………6分
=4.……………………………………………………………………7分
18.(本题8分)(1)100 ……………………………………………………………2分
(2)
…………………………………………………4分
(3)108 ………………………………………………………………………………6分
(4)600 ………………………………………………………………………………8分
19.(本题8分)
解:(1)设海绵飞盘的进货单价是x元,则橡胶飞盘的进货单价是(x+6)元, ……1分
由题意得:50(x+6)+30x=620, ……………………………………………………2分
解得:x=4, ……………………………………………………………………3分
∴6+4=10,
答:海绵飞盘的进货单价是4元,则橡胶飞盘的进货单价是10元 …………………4分
(备注:列二元一次方程组也可以);
(2)设第二批购进橡胶飞盘y个,则海绵飞盘购进(300﹣y)个,获得利润为w元,
∵y≤2(300﹣y),
∴0<y≤200, ……………………………………………………………………5分
由题意得:w=(14﹣10)y+(6﹣4)(300﹣y)=2y+600, ……………………6分
∵2>0,
∴w随y的增大而增大, ……………………………………………………………7分
∴当y=200时,w有最大值,w最大值=400+600=1000,
答:第二批购进橡胶飞盘200个时,总利润最大,最大利润是1000元. …………8分
20.(本题8分)回溯教材:北师大版九年级下册教材第41页《习题2.5》第4题
(1)13 59.9 ………………………………………………2分
(2)
(备注:描点1分,连线1分) ……………………………………………4分
(3)增强 降低 ………………………………………………………………6分
(4)当y=59时,﹣0.1x2+2.6x+43=59, …………………………………………7分
解得x1=10,x2=16,
答:某同学对概念的接受能力达到59时,他提出概念所用的时间是10分钟或16分钟.…8分
21.(本题9分)回溯教材:北师大版九年级下册教材第81页《习题3.4》第4题
(1)< < ………………………………………………………………………2分
(2)①∠AQB<∠APB;………………………3分
②记BQ与O相交于点H,连接AH,
∵=
∴∠APB=∠AHB, ………………………4分
∵∠AHB是△AHQ的外角,
∴∠AQB<∠AHB,
∴∠AQB<∠APB. ………………………5分
(3)方法一:由(2)知,过点A、B的圆O与PQ相切时,射门角度(∠AMB)最大,连接AM,AN,延长QP交AB的延长线于点G, …………………………………6分
在Rt△DPG中,∵∠DPG=∠QPC,
∴DG=7.5×=米,
PG=7.5×=米,GB=+15.5=米, …………………………7分
GA=+7=米,
∵∠GMB=∠GAM,
又∵∠G为公共角,
∴△GMB∽△GAM,
∴,
即 GM 2=GBGA,
GM 2=×,解得GM=米, ………………………………………8分
PM=﹣=15米
综上, PM的长度为15米. ………………………………………9分
方法二:由(2)知,过点A、B的圆O与PQ相切时,射门角度(∠AMB)最大,
∴∠OMF=90°, ………………………………………6分
如图,作AB的中垂线EF交AB于点E,交PQ于点F,则点O在线段EF上,
∴BE=7×=3.5米,则DE=3.5+15.5=19米,
过点F作FG ┴ CD于点G,
∴四边形EFGD是矩形,
∴FG=DE=19米,
在Rt△EPG中,PG==米,
sin∠QPC=,PF==米, …………………………………………7分
EF=DG=7.5+=米,
∵EF ∥DG ,
∴∠OFM=∠FPG ,
设圆O的半径为R,在Rt△OFM中,OF==R,
EO=﹣R,
∵OB2=OE2+EB2,
∴R2=(﹣R)2+3.52,解得R=(舍去)或, …………………8分
∴MF=米,
PM=﹣=15米.
综上, PM的长度为15米. …………………………………………………9分
22.(本题10分)回溯教材:北师大版九年级上册教材第25页《习题1.8》第4题
解:(1)∵四边形ABCD是正方形,
∴OC=OD,∠COD=90°,∠BCD=90°,
∴∠ODN=∠OCD=45°,
∴∠OCB=90°﹣45°=45°, …………1分
∵四边形A’B’C’O是正方形,
∴∠A’OC’=90°,
∴∠MOC+∠CO N=90°,
又∵∠NOD +∠CON=90°,
∴∠MOC=∠NOD, …………2分
在△OMC和△OND中,,
∴△OMC≌△OND. …………………………………………………3分
(2)∵四边形ABCD是矩形,
∴BC=AD=12,CD=AB=6,
AC=BD,OC=AD,OB=OD=BD,
∴OB=OC=OD,
过点O分别作OF┴ CD交CD于F, OE┴ BC交BC于点E, 则四边形OECF是矩形,
∴∠EOF=90°,OF=CE,OE=CF,
∵OB=OC, OE┴ BC,
∴CE=×12=6,
∵OD=OC, OF┴ DC,
∴CF=DF=×6=3,则FN=3﹣1=2,
∵四边形A’B’C’O是矩形,
∴∠A’OC’=90°,
∴∠MOF+∠FON=90°,
又∵∠MOF +∠MOE=90°, ……………………………………………4分
∴∠FON=∠MOE,
又∵∠OFN=∠OEM=90°,
∴△OFN∽△OEM, ……………………………………………5分
∴,则EM=1,
∴CM=6﹣1=5. ……………………………………………………6分
(3)或 ………………………………………………………………………10分
(备注:每种情况各2分)
解析:①当∠BDC=90°时,如图1,△ODN∽△OEM,且相似比为:1,
可求得OE=,BE=,
设ME=x,则DN=x,CN=3﹣x,
∵ ABCD与 A’B’C’O重叠部分的面积是 ABCD的面积的,
∴S△OC N = S△OBM,则BM=CN=(3﹣x),
∵(3﹣x)+ x=,
∴x=,则DN=,
在Rt△ODN中,ON=,
图1 图2
②当∠BDC=90°时,如图2,ON是△BCD的中位线,于是ON=.
第 3页,共 9页
同课章节目录
