11.3.1多边形导学案
图片预览

文档简介
章名:第11章三角形
课题:11.3.1多边形
主备人:吴翠华
教学目标:1、了解多边形及有关概念,理解正多边形及其有关的概念.
2、区别凸多边形与凹多边形.
教学重点:多边形及有关概念、正多边形的概念
教学难点:1.区别凸多边形与凹多边形。
2.确定多边形对角线条数。
一、预习案
1.看书本19页图片,你能从中找出由一些线段围成的图形吗?
2.这些图形有什么特点?
在平面内,由不在同一直线上的 叫做多边形,
这些线段称为多边形的 。
三角形是平面内由 条不在同一直线上的线段首尾顺次连结组成的图形;
四边形是平面内由 条不在同一直线上的线段首尾顺次连结组成的图形;
五边形是平面内由 条不在同一直线上的线段首尾顺次连结组成的图形;
……
边形是平面内由 条不在同一直线上的线段首尾顺次连结组成的图形。
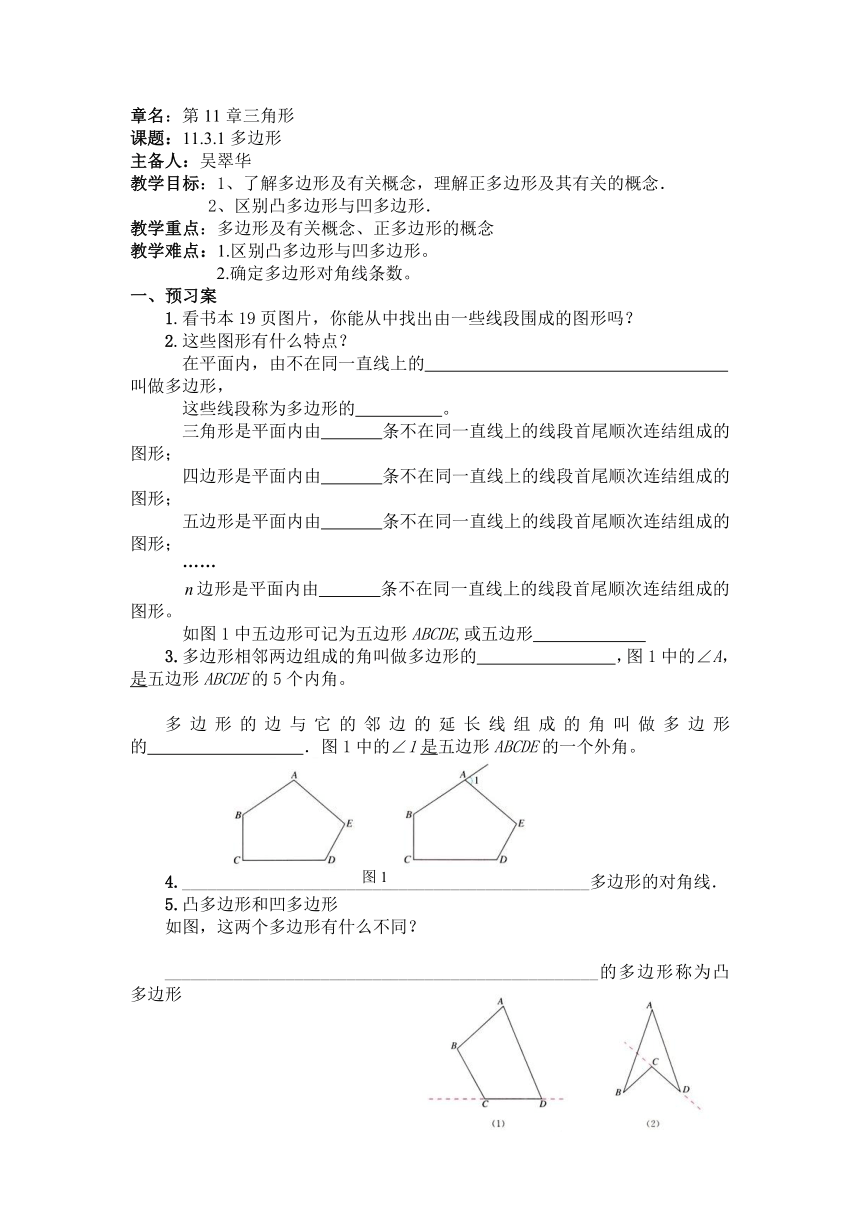
如图1中五边形可记为五边形ABCDE,或五边形
3.多边形相邻两边组成的角叫做多边形的 ,图1中的∠A, 是五边形ABCDE的5个内角。
多边形的边与它的邻边的延长线组成的角叫做多边形的 .图1中的∠1是五边形ABCDE的一个外角。
4._______________________________________________多边形的对角线.
5.凸多边形和凹多边形
如图,这两个多边形有什么不同?
__________________________________________________的多边形称为凸多边形
____________________________________________________我们称它为凹多边形。
注意:今后我们讨论的多边形指的都是凸多边形.
6.正多边形的概念
______________________________________________________的多边形叫做正多边形。
二.导学案
探究点1 多边形的概念
(一)知识讲解:在平面内,由不在同一条直 ( http: / / www.21cnjy.com )线上的一些线段首尾顺次相接组成的封闭图形叫做多边形。多边形是按边定义的,最简单的多边形是三角形。我们只研究凸多边形。
探究点2 多边形的对角线
(一)知识讲解:
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
2. 三角形从一个顶点出发,能引出 条对角线;
四边形从一个顶点出发,能引出 条对角线;
五边形从一个顶点出发,能引出 条对角线;
六边形从一个顶点出发,能引出 条对角线;
……
边形从一个顶点出发,能引出 条对角线;
四边形共有 条对角线;
五边形共有 条对角线;画图看看。
……
你能猜想边形共有 条对角线,说说你的想法。
规律: n边形对角线的总条数为n(n-3)/2.
探究点3 多边形的内角、外角、正多边形
(一)知识讲解:
1. 多边形相邻两边组成的角叫做多边形的内角。多边形的边与它的邻边的延长线组成的角叫做多边形的外角。n边形有个n内角,2n个外角.
2.各个角都相等,各条边都相等的多边形叫做正多边形。
三.概括整合
边(条数) 内角(个数) 外角(个数) 对角线(条数)
三角形 3 3 6 0
四边形 4 4 8 2
五边形 5 5 10 5
n边形 n n 2n n(n-3)/2
正n边形 n n 2n n(n-3)/2
三.检测案
(一)典例剖析:
例1:下列结论正确的是( )
A.在平面内,有四条线段组成的图形叫做四边形。
B.由不在同一直线上的四条线段组成的图形叫做四边形
C.在平面内,由不在同一直线上的四条线段组成的图形叫做四边形
D.在平面内,由不在同一直线上的四条线段首尾顺次相接组成的图形叫做四边形。
例2:(1)十边形的对角线有__条。
(2)如果经过多边形的一个顶点有36条对角线,则这个多边形有__条边。
例3:下列图形中,是正多边形的是( )
A.直角三角形 B.等腰三角形 C.长方形 D.正方形
(二)类题突破:
1.下列图中不是凸多边形的是( )
2.过m边形的一个顶点有7条对角线,n边形没有对角线,则n-m=
3.一个四边形截去一个角后内角个数是( )
A.3 B.4 C.5 D.3、4、5
四.课堂练习:P21练习1.2
五.课堂小结:本节课学习了多边形定义及有关 ( http: / / www.21cnjy.com )概念、正多边形的概念,重点探究多边形边数与对角线条数的关系,以及过n边形的一个顶点可作出n-3条对角线。
六.课后反思:
图1
A
B
C
D
课题:11.3.1多边形
主备人:吴翠华
教学目标:1、了解多边形及有关概念,理解正多边形及其有关的概念.
2、区别凸多边形与凹多边形.
教学重点:多边形及有关概念、正多边形的概念
教学难点:1.区别凸多边形与凹多边形。
2.确定多边形对角线条数。
一、预习案
1.看书本19页图片,你能从中找出由一些线段围成的图形吗?
2.这些图形有什么特点?
在平面内,由不在同一直线上的 叫做多边形,
这些线段称为多边形的 。
三角形是平面内由 条不在同一直线上的线段首尾顺次连结组成的图形;
四边形是平面内由 条不在同一直线上的线段首尾顺次连结组成的图形;
五边形是平面内由 条不在同一直线上的线段首尾顺次连结组成的图形;
……
边形是平面内由 条不在同一直线上的线段首尾顺次连结组成的图形。
如图1中五边形可记为五边形ABCDE,或五边形
3.多边形相邻两边组成的角叫做多边形的 ,图1中的∠A, 是五边形ABCDE的5个内角。
多边形的边与它的邻边的延长线组成的角叫做多边形的 .图1中的∠1是五边形ABCDE的一个外角。
4._______________________________________________多边形的对角线.
5.凸多边形和凹多边形
如图,这两个多边形有什么不同?
__________________________________________________的多边形称为凸多边形
____________________________________________________我们称它为凹多边形。
注意:今后我们讨论的多边形指的都是凸多边形.
6.正多边形的概念
______________________________________________________的多边形叫做正多边形。
二.导学案
探究点1 多边形的概念
(一)知识讲解:在平面内,由不在同一条直 ( http: / / www.21cnjy.com )线上的一些线段首尾顺次相接组成的封闭图形叫做多边形。多边形是按边定义的,最简单的多边形是三角形。我们只研究凸多边形。
探究点2 多边形的对角线
(一)知识讲解:
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
2. 三角形从一个顶点出发,能引出 条对角线;
四边形从一个顶点出发,能引出 条对角线;
五边形从一个顶点出发,能引出 条对角线;
六边形从一个顶点出发,能引出 条对角线;
……
边形从一个顶点出发,能引出 条对角线;
四边形共有 条对角线;
五边形共有 条对角线;画图看看。
……
你能猜想边形共有 条对角线,说说你的想法。
规律: n边形对角线的总条数为n(n-3)/2.
探究点3 多边形的内角、外角、正多边形
(一)知识讲解:
1. 多边形相邻两边组成的角叫做多边形的内角。多边形的边与它的邻边的延长线组成的角叫做多边形的外角。n边形有个n内角,2n个外角.
2.各个角都相等,各条边都相等的多边形叫做正多边形。
三.概括整合
边(条数) 内角(个数) 外角(个数) 对角线(条数)
三角形 3 3 6 0
四边形 4 4 8 2
五边形 5 5 10 5
n边形 n n 2n n(n-3)/2
正n边形 n n 2n n(n-3)/2
三.检测案
(一)典例剖析:
例1:下列结论正确的是( )
A.在平面内,有四条线段组成的图形叫做四边形。
B.由不在同一直线上的四条线段组成的图形叫做四边形
C.在平面内,由不在同一直线上的四条线段组成的图形叫做四边形
D.在平面内,由不在同一直线上的四条线段首尾顺次相接组成的图形叫做四边形。
例2:(1)十边形的对角线有__条。
(2)如果经过多边形的一个顶点有36条对角线,则这个多边形有__条边。
例3:下列图形中,是正多边形的是( )
A.直角三角形 B.等腰三角形 C.长方形 D.正方形
(二)类题突破:
1.下列图中不是凸多边形的是( )
2.过m边形的一个顶点有7条对角线,n边形没有对角线,则n-m=
3.一个四边形截去一个角后内角个数是( )
A.3 B.4 C.5 D.3、4、5
四.课堂练习:P21练习1.2
五.课堂小结:本节课学习了多边形定义及有关 ( http: / / www.21cnjy.com )概念、正多边形的概念,重点探究多边形边数与对角线条数的关系,以及过n边形的一个顶点可作出n-3条对角线。
六.课后反思:
图1
A
B
C
D
