10.5 图形的全等 教案
图片预览


文档简介
中小学教育资源及组卷应用平台
10.5 图形的全等 教学设计
课题 10.4 中心对称 单元 第10 单元 学科 数学 年级 七年级(下)
教材分析 了解图形全等的意义.了解图形全等的特征.识别全等图形.体会图形的三种基本变换与图形全等的关系.
核心素养分析 借助具体情境和图案,经历观察、发现和实践操作重叠图形等过程.激发学生探究图形全等的兴趣.培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识.
学习目标 1.了解全等图形的概念及性质,体会图形的三种基本变换与图形全等的关系.2.了解全等多边形的概念、性质及判定,能辨别全等多边形的对应元素.3.了解全等三角形的概念、性质及判定.
重点 了解全等图形的概念及性质,体会图形的三种基本变换与图形全等的关系.
难点 了解全等三角形的概念、性质及判定.
教学过程
教学环节 教师活动 学生活动 设计意图
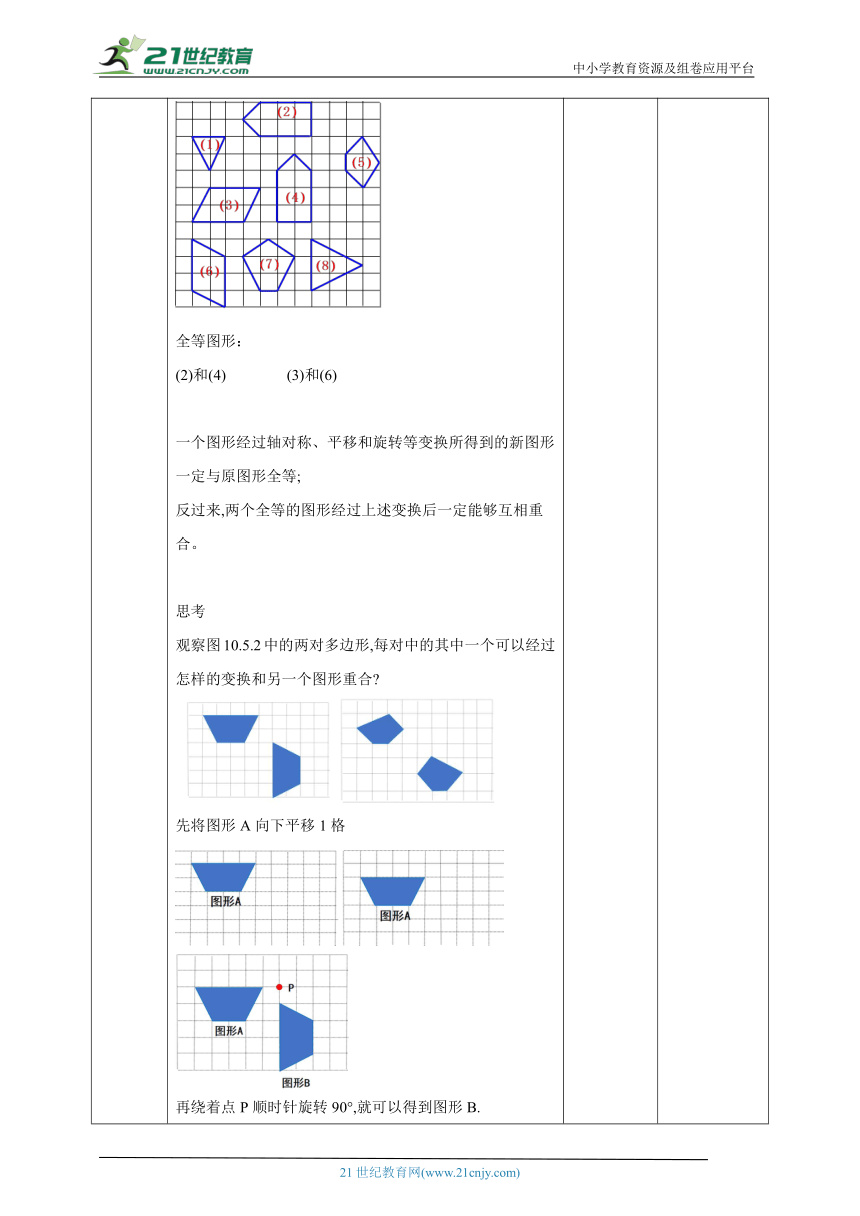
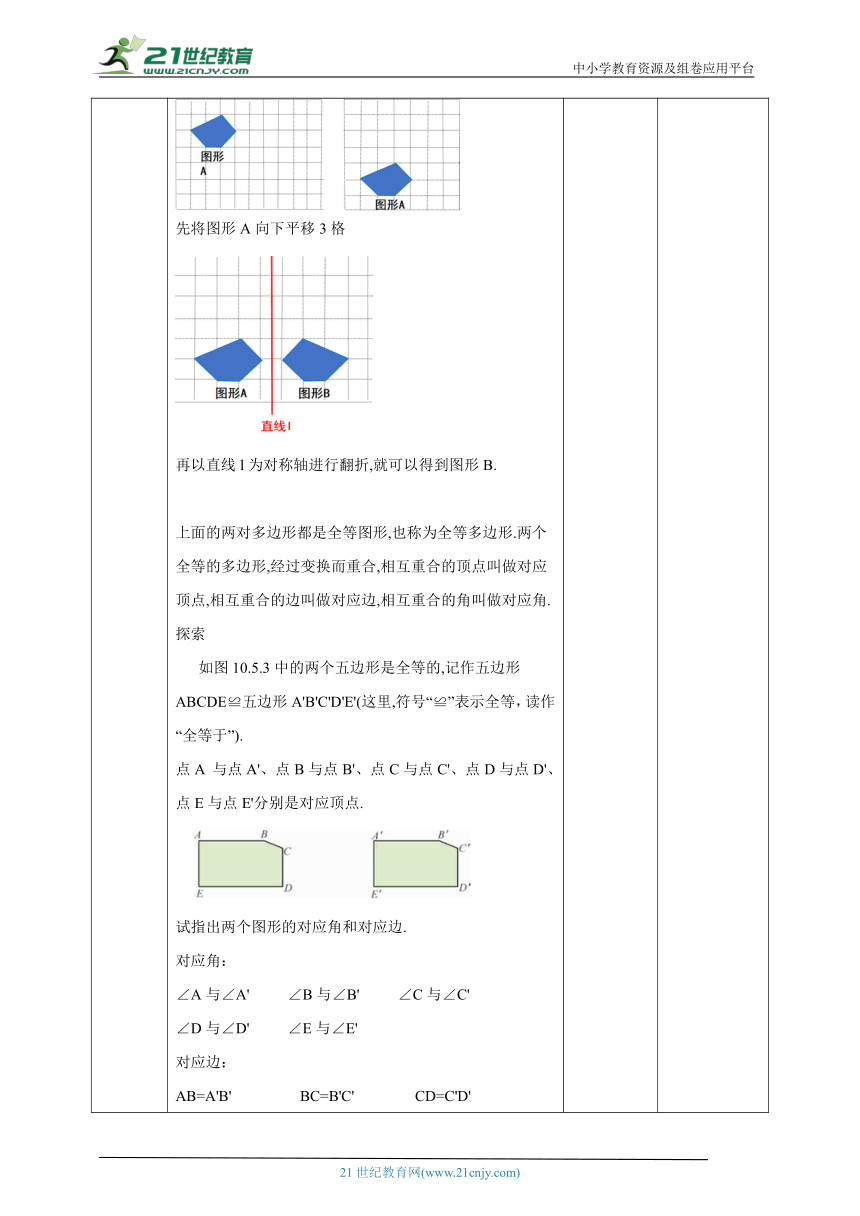
导入新课 一、创设情景,引出课题图形的轴对称、平移和旋转,这是图形的三种基本变换有什么共同点呢?图形经过这样的变换,位置发生了改变,但变换前后两个图形的对应线段相等,对应角相等,图形的形状和大小并没有改变.要想知道两个图形的形状和大小是否完全相同,可以通过轴对称、平移和旋转这些图形的变换,把两个图形叠合在一起,观察它们是否完全重合.能够完全重合的两个图形叫做全等图形.做一做图10.5.1中给出了8个图形,你能发现哪两个图形是全等图形吗 动手试试看.全等图形:(2)和(4) (3)和(6)一个图形经过轴对称、平移和旋转等变换所得到的新图形一定与原图形全等;反过来,两个全等的图形经过上述变换后一定能够互相重合。思考观察图10.5.2中的两对多边形,每对中的其中一个可以经过怎样的变换和另一个图形重合 先将图形A向下平移1格再绕着点P顺时针旋转90°,就可以得到图形B.先将图形A向下平移3格再以直线l为对称轴进行翻折,就可以得到图形B.上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.探索 如图10.5.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A'B'C'D'E'(这里,符号“≌”表示全等,读作“全等于”).点A 与点A'、点B与点B'、点C与点C'、点D与点D'、点E与点E'分别是对应顶点. 试指出两个图形的对应角和对应边.对应角:∠A与∠A' ∠B与∠B' ∠C与∠C'∠D与∠D' ∠E与∠E'对应边:AB=A'B' BC=B'C' CD=C'D'DE=D'E' EA=E'A'依据上面的分析,我们知道:全等多边形的对应边相等,对应角相等.这就是全等多边形的性质.实际上,边、角分别对应相等这两个特征足以刻画多边形的全等了.也就是说,在数学上我们可以给出全等多边形如下的定义:边、角分别对应相等的两个多边形称为全等多边形.这个定义是我们判断两个多边形是否全等的准确方法.三角形是特殊的多边形,因此,全等三角形的对应边、对应角分别相等.同样,我们也可以得到全等三角形的定义,从而也得到了判断两个三角形是否全等的准确方法:如果两个三角形的边、角分别对应相等,那么这两个三角形全等.如图10.5.4所示,△ABC≌△DEF,且 ∠A=∠D,∠B = ∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗 对应顶点:点A与点D,点B与点E,点C与点F,对应角:∠A与∠D,∠B与∠E,∠C与∠F,对应边:AB与DE AC与DF BC与FE请同学们找出图中全等三角形的对应角对应角:∠CAD与∠BAE ∠ACD与∠ABE ∠ADC与∠AEB对应角:∠BAC与∠EDF ∠ABC与∠DEF ∠ACB与∠DFE对应角:∠AOC与∠BOD ∠ACO与∠BDO ∠CAO与∠DBO 思考自议以问题导入,吸引学生注意力,复习上节内容,导入本节新内容--图形的全等。 引入新课,激发学生探究图形全等的兴趣。
讲授新课 提炼概念全等三角形对应边、对应角的求法:1、利用字母的对应位置来确定对应边和对应角。2、在图上找特殊的边和特殊的角:有公共角的,公共角是对应角;有对顶角的,对顶角是对应角。3、对应边所对的角是对应角,对应角所对的边是对应边。三、典例精讲例 如图10.5.5,△ABC沿着BC的方向平移至△DEF,∠A =80°,∠B=60°,求∠F的度数.解 由图形平移的特征,可知△ABC与ADEF的形状与大小相同,即△ABC≌△DEF.∴∠D=∠A=80°(全等三角形的对应角相等).同理∠DEF=∠B=60°.又∵∠D+∠DEF+ ∠F = 180°(三角形的内角和等于180°),∴∠F=180°-∠D-∠DEF=180°-80°-60°=40°. 通过例题来巩固、强化课堂上所学的知识,并且培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识。 总结图形的全等的定义和特征, 激发学生探究图形的全等,加深对图形全等定义的理解。
课堂练习 四、巩固训练1.下列说法中正确的有( )①用一张底片冲洗出来的10张1寸相片是全等形;②我国国旗上的4颗小五角星是全等形;③所有的正方形是全等形;④全等形的面积一定相等.A.1个 B.2个 C.3个 D.4个C2.如图所示,△AOC≌△BOD,点A与点B,点C与点D是对应点,下列结论中错误的是( ) A.∠A与∠B是对应角 B.∠AOC与∠BOD是对应角 C.OC与OB是对应边 D.OC与OD是对应边C3.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( ) A.∠1=∠2 B.∠ACB=∠CAD C.AB=AD D.∠B=∠DC已知△ABC≌△DEF, △ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度.解:∵ △ABC≌△DEF (已知) ∴AC=DF(全等三角形的对应边相等) ∵△ABC的周长是40cm, AB=10cm,BC=16cm (已知) ∴ AC=40-10-16=14(cm) ∴ DF=14cm5.如图所示,△ABC与△DEC全等,且∠ACB=90°.(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角;解:△ABC与△DEC全等,观察图形发现可将△ABC绕点C顺时针旋转90°得到△DEC.对应边:AB与DE,AC与DC,BC与EC,对应角:∠A与∠D,∠ACB与∠DCE,∠ABC与∠E.(2)请直接写出直线AB、DE的位置关系.解:直线AB、DE互相垂直.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
10.5 图形的全等 教学设计
课题 10.4 中心对称 单元 第10 单元 学科 数学 年级 七年级(下)
教材分析 了解图形全等的意义.了解图形全等的特征.识别全等图形.体会图形的三种基本变换与图形全等的关系.
核心素养分析 借助具体情境和图案,经历观察、发现和实践操作重叠图形等过程.激发学生探究图形全等的兴趣.培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识.
学习目标 1.了解全等图形的概念及性质,体会图形的三种基本变换与图形全等的关系.2.了解全等多边形的概念、性质及判定,能辨别全等多边形的对应元素.3.了解全等三角形的概念、性质及判定.
重点 了解全等图形的概念及性质,体会图形的三种基本变换与图形全等的关系.
难点 了解全等三角形的概念、性质及判定.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题图形的轴对称、平移和旋转,这是图形的三种基本变换有什么共同点呢?图形经过这样的变换,位置发生了改变,但变换前后两个图形的对应线段相等,对应角相等,图形的形状和大小并没有改变.要想知道两个图形的形状和大小是否完全相同,可以通过轴对称、平移和旋转这些图形的变换,把两个图形叠合在一起,观察它们是否完全重合.能够完全重合的两个图形叫做全等图形.做一做图10.5.1中给出了8个图形,你能发现哪两个图形是全等图形吗 动手试试看.全等图形:(2)和(4) (3)和(6)一个图形经过轴对称、平移和旋转等变换所得到的新图形一定与原图形全等;反过来,两个全等的图形经过上述变换后一定能够互相重合。思考观察图10.5.2中的两对多边形,每对中的其中一个可以经过怎样的变换和另一个图形重合 先将图形A向下平移1格再绕着点P顺时针旋转90°,就可以得到图形B.先将图形A向下平移3格再以直线l为对称轴进行翻折,就可以得到图形B.上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.探索 如图10.5.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A'B'C'D'E'(这里,符号“≌”表示全等,读作“全等于”).点A 与点A'、点B与点B'、点C与点C'、点D与点D'、点E与点E'分别是对应顶点. 试指出两个图形的对应角和对应边.对应角:∠A与∠A' ∠B与∠B' ∠C与∠C'∠D与∠D' ∠E与∠E'对应边:AB=A'B' BC=B'C' CD=C'D'DE=D'E' EA=E'A'依据上面的分析,我们知道:全等多边形的对应边相等,对应角相等.这就是全等多边形的性质.实际上,边、角分别对应相等这两个特征足以刻画多边形的全等了.也就是说,在数学上我们可以给出全等多边形如下的定义:边、角分别对应相等的两个多边形称为全等多边形.这个定义是我们判断两个多边形是否全等的准确方法.三角形是特殊的多边形,因此,全等三角形的对应边、对应角分别相等.同样,我们也可以得到全等三角形的定义,从而也得到了判断两个三角形是否全等的准确方法:如果两个三角形的边、角分别对应相等,那么这两个三角形全等.如图10.5.4所示,△ABC≌△DEF,且 ∠A=∠D,∠B = ∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗 对应顶点:点A与点D,点B与点E,点C与点F,对应角:∠A与∠D,∠B与∠E,∠C与∠F,对应边:AB与DE AC与DF BC与FE请同学们找出图中全等三角形的对应角对应角:∠CAD与∠BAE ∠ACD与∠ABE ∠ADC与∠AEB对应角:∠BAC与∠EDF ∠ABC与∠DEF ∠ACB与∠DFE对应角:∠AOC与∠BOD ∠ACO与∠BDO ∠CAO与∠DBO 思考自议以问题导入,吸引学生注意力,复习上节内容,导入本节新内容--图形的全等。 引入新课,激发学生探究图形全等的兴趣。
讲授新课 提炼概念全等三角形对应边、对应角的求法:1、利用字母的对应位置来确定对应边和对应角。2、在图上找特殊的边和特殊的角:有公共角的,公共角是对应角;有对顶角的,对顶角是对应角。3、对应边所对的角是对应角,对应角所对的边是对应边。三、典例精讲例 如图10.5.5,△ABC沿着BC的方向平移至△DEF,∠A =80°,∠B=60°,求∠F的度数.解 由图形平移的特征,可知△ABC与ADEF的形状与大小相同,即△ABC≌△DEF.∴∠D=∠A=80°(全等三角形的对应角相等).同理∠DEF=∠B=60°.又∵∠D+∠DEF+ ∠F = 180°(三角形的内角和等于180°),∴∠F=180°-∠D-∠DEF=180°-80°-60°=40°. 通过例题来巩固、强化课堂上所学的知识,并且培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识。 总结图形的全等的定义和特征, 激发学生探究图形的全等,加深对图形全等定义的理解。
课堂练习 四、巩固训练1.下列说法中正确的有( )①用一张底片冲洗出来的10张1寸相片是全等形;②我国国旗上的4颗小五角星是全等形;③所有的正方形是全等形;④全等形的面积一定相等.A.1个 B.2个 C.3个 D.4个C2.如图所示,△AOC≌△BOD,点A与点B,点C与点D是对应点,下列结论中错误的是( ) A.∠A与∠B是对应角 B.∠AOC与∠BOD是对应角 C.OC与OB是对应边 D.OC与OD是对应边C3.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( ) A.∠1=∠2 B.∠ACB=∠CAD C.AB=AD D.∠B=∠DC已知△ABC≌△DEF, △ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度.解:∵ △ABC≌△DEF (已知) ∴AC=DF(全等三角形的对应边相等) ∵△ABC的周长是40cm, AB=10cm,BC=16cm (已知) ∴ AC=40-10-16=14(cm) ∴ DF=14cm5.如图所示,△ABC与△DEC全等,且∠ACB=90°.(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角;解:△ABC与△DEC全等,观察图形发现可将△ABC绕点C顺时针旋转90°得到△DEC.对应边:AB与DE,AC与DC,BC与EC,对应角:∠A与∠D,∠ACB与∠DCE,∠ABC与∠E.(2)请直接写出直线AB、DE的位置关系.解:直线AB、DE互相垂直.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
