10.5 图形的全等 课件(共31张PPT)
文档属性
| 名称 | 10.5 图形的全等 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-29 23:27:19 | ||
图片预览










文档简介
(共31张PPT)
10.5 图形的全等
华师大版 七年级 下册
教学目标
教学目标:1.知道全等图形,全等多边形,全等三角形的概念和性质.
2.能找出全等多边形、全等三角形的对应元素,会利用图形的
全等解决一些简单问题
教学重点:了解全等图形的概念及性质,体会图形的三种基本变换与图形全等
的关系.
教学难点:了解全等三角形的概念、性质及判定.
新知导入
情境引入
我们学过哪三种基本变换?它们有什么特征?轴对称(翻折)、平移、旋转
D
l
A
B
C
E
F
A
B
C
D
F
E
·
O
A
B
C
D
E
F
这三种基本变换中, △ABC与△DEF都能重合吗?
作△ABC关于直线l对称的△DEF
作△ABC向右平移
4格的△DEF
作△ABC绕点O顺时针旋转90°的△DEF
新知讲解
合作学习
图形经过这样的变换,位置发生了改变,但变换前后两个图形的对应线段相等,对应角相等,图形的形状和大小并没有改变.
图形的轴对称、平移和旋转,这是图形的三种基本变换,它们有什么共同点呢?
轴对称、平移与旋转都是实际生活中抽象得到的一些基本变换,它们保证了变换过程中,任意两点之间的距离不变,从而保证了图形的形状与大小都不发生变化,反映了图形之间的全等关系.
读一读
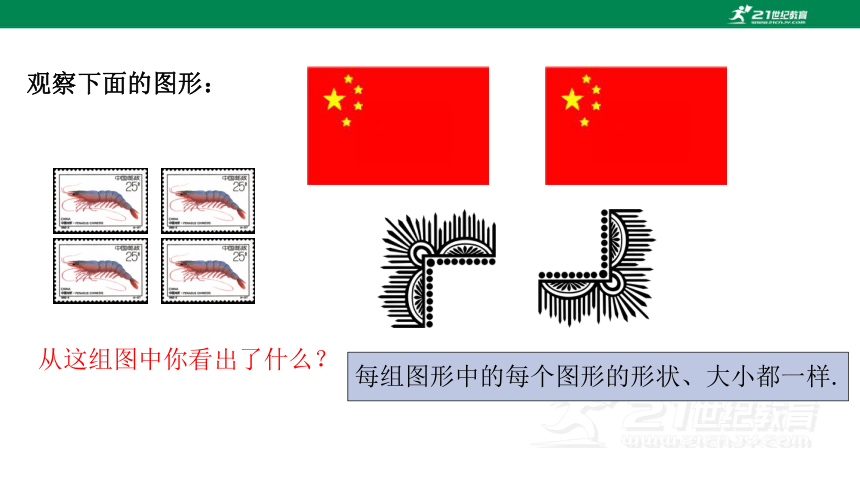
观察下面的图形:
从这组图中你看出了什么?
每组图形中的每个图形的形状、大小都一样.
全等图形的定义:
能够完全重合的两个图形叫做全等图形.
归纳
探究新知
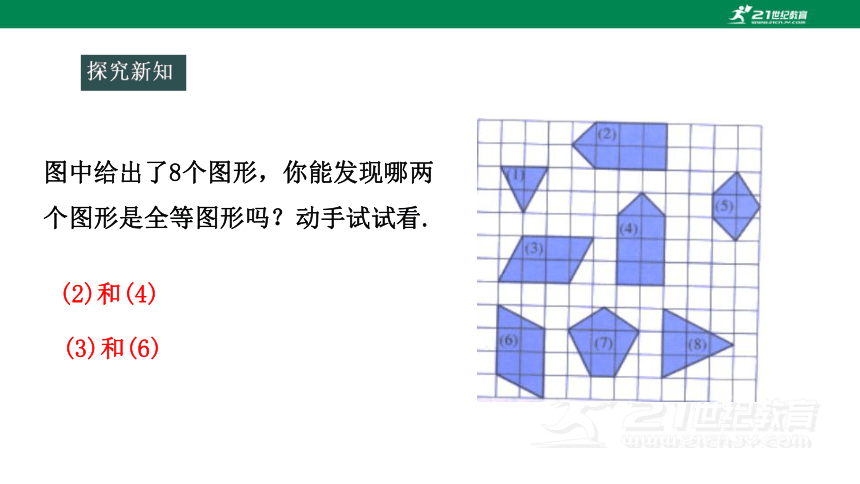
图中给出了8个图形,你能发现哪两个图形是全等图形吗?动手试试看.
(2)和(4)
(3)和(6)
一个图形经过轴对称、平移和旋转等变换所得到的新图形一定与原图形全等;
两个全等的图形经过上述变换后一定能够互相重合.
归纳总结
思考
观察下图中的两对多边形,每对中的其中一个可以经过怎样的变换和
另一个图形重合?
概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
探索
如图10.5.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A'B'C'D'E'(这里,符号“≌”表示全等,读作“全等于”).
图10.5.3
BC B1C1
EA E1A1
=
=
=
∠B ∠B1
=
此符号表示全等,读作“全等于”.
探索
点A 与点A'、点B与点B'、点C与点C'、点D与点D'、点E与点E'分别是对应顶点.
图10.5.3
试指出两个图形的对应角和对应边.
图10.5.3
对应角:
∠A与∠A'
∠B与∠B'
∠C与∠C'
∠D与∠D'
∠E与∠E'
图10.5.3
对应边:
AB=A'B'
BC=B'C'
CD=C'D'
DE=D'E'
EA=E'A'
全等多边形的性质:
全等多边形的对应边、对应角分别相等.
全等多边形的判定方法:
如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
如图10.5.4所示,△ABC≌△DEF,且 ∠A=∠D,∠B = ∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗
图10.5.4
图10.5.4
对应顶点:
点A与点D,
点B与点E,
点C与点F,
对应角:
∠A与∠D,
∠B与∠E,
∠C与∠F,
对应边:
AB与DE
AC与DF
BC与FE
C
D
A
B
E
A
B
C
D
E
F
请同学们找出图中全等三角形的对应角
△ACD≌△ABE
△ABC≌△DEF
△AOC≌△BOD
B
D
A
C
O
提炼概念
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;
典例精讲
A
B
C
D
E
F
例:如图,△ABC沿着BC的方向平移至 △DEF,∠A=80°, ∠B=60°,求∠F的度数.
解:由图形平移的特征,可知△ABC与△DEF的形状和大小相同,即△ABC ≌△DEF
∴ ∠D=∠A=80°
同理∠DEF= ∠B=60°.
又∵ ∠D+∠DEF+∠F=180°
∴ ∠F=180 °- ∠D-∠DEF=40°
归纳概念
确定两个图形是否全等:
(1)运用定义识别全等图形,确定两个图形全等要符合两个条件:①形状相同,②大小相等;
(2)判断两个图形是否全等还可以通过平移、旋转、翻折等方法把两个图形叠合在一起,看它们能否重合,即用叠合法判断.
课堂练习
1.下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等形;
②我国国旗上的4颗小五角星是全等形;
③所有的正方形是全等形;
④全等形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
C
2.如图所示,△AOC≌△BOD,点A与点B,点C与点D是对应点,下列结论中错误的是( )
A.∠A与∠B是对应角
B.∠AOC与∠BOD是对应角
C.OC与OB是对应边
D.OC与OD是对应边
C
3.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.∠ACB=∠CAD
C.AB=AD
D.∠B=∠D
C
4.已知△ABC≌△DEF, △ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度.
解:∵ △ABC≌△DEF (已知)
∴AC=DF(全等三角形的对应边相等)
∵△ABC的周长是40cm, AB=10cm,BC=16cm (已知)
∴ AC=40-10-16=14(cm)
∴ DF=14cm
多动脑筋多
想方法
A
B
C
D
E
F
5.如图所示,△ABC与△DEC全等,且∠ACB=90°.
(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角;
解:△ABC与△DEC全等,观察图形发现可将△ABC绕点C顺时针旋转90°得到△DEC.
对应边:AB与DE,AC与DC,BC与EC,
对应角:∠A与∠D,∠ACB与∠DCE,∠ABC与∠E.
(2)请直接写出直线AB、DE的位置关系.
解:直线AB、DE互相垂直.
课堂总结
全等图形
概念
对应点、对应角、对应边
性质
对应角相等,对应边相等
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
10.5 图形的全等
华师大版 七年级 下册
教学目标
教学目标:1.知道全等图形,全等多边形,全等三角形的概念和性质.
2.能找出全等多边形、全等三角形的对应元素,会利用图形的
全等解决一些简单问题
教学重点:了解全等图形的概念及性质,体会图形的三种基本变换与图形全等
的关系.
教学难点:了解全等三角形的概念、性质及判定.
新知导入
情境引入
我们学过哪三种基本变换?它们有什么特征?轴对称(翻折)、平移、旋转
D
l
A
B
C
E
F
A
B
C
D
F
E
·
O
A
B
C
D
E
F
这三种基本变换中, △ABC与△DEF都能重合吗?
作△ABC关于直线l对称的△DEF
作△ABC向右平移
4格的△DEF
作△ABC绕点O顺时针旋转90°的△DEF
新知讲解
合作学习
图形经过这样的变换,位置发生了改变,但变换前后两个图形的对应线段相等,对应角相等,图形的形状和大小并没有改变.
图形的轴对称、平移和旋转,这是图形的三种基本变换,它们有什么共同点呢?
轴对称、平移与旋转都是实际生活中抽象得到的一些基本变换,它们保证了变换过程中,任意两点之间的距离不变,从而保证了图形的形状与大小都不发生变化,反映了图形之间的全等关系.
读一读
观察下面的图形:
从这组图中你看出了什么?
每组图形中的每个图形的形状、大小都一样.
全等图形的定义:
能够完全重合的两个图形叫做全等图形.
归纳
探究新知
图中给出了8个图形,你能发现哪两个图形是全等图形吗?动手试试看.
(2)和(4)
(3)和(6)
一个图形经过轴对称、平移和旋转等变换所得到的新图形一定与原图形全等;
两个全等的图形经过上述变换后一定能够互相重合.
归纳总结
思考
观察下图中的两对多边形,每对中的其中一个可以经过怎样的变换和
另一个图形重合?
概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
探索
如图10.5.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A'B'C'D'E'(这里,符号“≌”表示全等,读作“全等于”).
图10.5.3
BC B1C1
EA E1A1
=
=
=
∠B ∠B1
=
此符号表示全等,读作“全等于”.
探索
点A 与点A'、点B与点B'、点C与点C'、点D与点D'、点E与点E'分别是对应顶点.
图10.5.3
试指出两个图形的对应角和对应边.
图10.5.3
对应角:
∠A与∠A'
∠B与∠B'
∠C与∠C'
∠D与∠D'
∠E与∠E'
图10.5.3
对应边:
AB=A'B'
BC=B'C'
CD=C'D'
DE=D'E'
EA=E'A'
全等多边形的性质:
全等多边形的对应边、对应角分别相等.
全等多边形的判定方法:
如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
如图10.5.4所示,△ABC≌△DEF,且 ∠A=∠D,∠B = ∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗
图10.5.4
图10.5.4
对应顶点:
点A与点D,
点B与点E,
点C与点F,
对应角:
∠A与∠D,
∠B与∠E,
∠C与∠F,
对应边:
AB与DE
AC与DF
BC与FE
C
D
A
B
E
A
B
C
D
E
F
请同学们找出图中全等三角形的对应角
△ACD≌△ABE
△ABC≌△DEF
△AOC≌△BOD
B
D
A
C
O
提炼概念
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;
典例精讲
A
B
C
D
E
F
例:如图,△ABC沿着BC的方向平移至 △DEF,∠A=80°, ∠B=60°,求∠F的度数.
解:由图形平移的特征,可知△ABC与△DEF的形状和大小相同,即△ABC ≌△DEF
∴ ∠D=∠A=80°
同理∠DEF= ∠B=60°.
又∵ ∠D+∠DEF+∠F=180°
∴ ∠F=180 °- ∠D-∠DEF=40°
归纳概念
确定两个图形是否全等:
(1)运用定义识别全等图形,确定两个图形全等要符合两个条件:①形状相同,②大小相等;
(2)判断两个图形是否全等还可以通过平移、旋转、翻折等方法把两个图形叠合在一起,看它们能否重合,即用叠合法判断.
课堂练习
1.下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等形;
②我国国旗上的4颗小五角星是全等形;
③所有的正方形是全等形;
④全等形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
C
2.如图所示,△AOC≌△BOD,点A与点B,点C与点D是对应点,下列结论中错误的是( )
A.∠A与∠B是对应角
B.∠AOC与∠BOD是对应角
C.OC与OB是对应边
D.OC与OD是对应边
C
3.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.∠ACB=∠CAD
C.AB=AD
D.∠B=∠D
C
4.已知△ABC≌△DEF, △ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度.
解:∵ △ABC≌△DEF (已知)
∴AC=DF(全等三角形的对应边相等)
∵△ABC的周长是40cm, AB=10cm,BC=16cm (已知)
∴ AC=40-10-16=14(cm)
∴ DF=14cm
多动脑筋多
想方法
A
B
C
D
E
F
5.如图所示,△ABC与△DEC全等,且∠ACB=90°.
(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角;
解:△ABC与△DEC全等,观察图形发现可将△ABC绕点C顺时针旋转90°得到△DEC.
对应边:AB与DE,AC与DC,BC与EC,
对应角:∠A与∠D,∠ACB与∠DCE,∠ABC与∠E.
(2)请直接写出直线AB、DE的位置关系.
解:直线AB、DE互相垂直.
课堂总结
全等图形
概念
对应点、对应角、对应边
性质
对应角相等,对应边相等
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
