七年级下册数学北师大版第六章概率初步单元测试(含答案)
文档属性
| 名称 | 七年级下册数学北师大版第六章概率初步单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 129.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-29 20:06:50 | ||
图片预览



文档简介
第六章概率初步(单元测试)
一、单选题(本大题共12小题,每小题3分,共36分)
1.如图,一个圆形转盘被平均分成6个全等的扇形,任意旋转这个转盘1次,则当转盘停止转动时,指针指向阴影部分的概率是( )
A. B. C. D.
2.下列事件中是必然事件的为:( )
A.连续抛一枚均匀硬币2次,有1次正面朝上
B.二次函数图象与x轴总有交点
C.所有的等腰直角三角形都是相似的
D.通过旋转变换得到的图形,也可以通过平移变换得到
3.如图,一副普通扑克牌中的13张黑桃牌(J代表11,Q代表12,K代表13),将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数是2的倍数的概率为( )
A. B. C. D.
4.盒子里有10个球,它们只有颜色不同,其中红球有7个,黄球有2个,黑球有1个.幸幸从中任意摸一个球,下面说法正确的是( )
A.一定是红球 B.摸出红球的可能性最大
C.不可能是黑球 D.摸出黄球的可能性最小
5.对于事件“某学习小组14人中至少有2人在同一个月过生日”,从发生的可能性大小判断,你认为该事件属于( )
A.不可能事件 B.随机事件 C.必然事件 D.无法判断
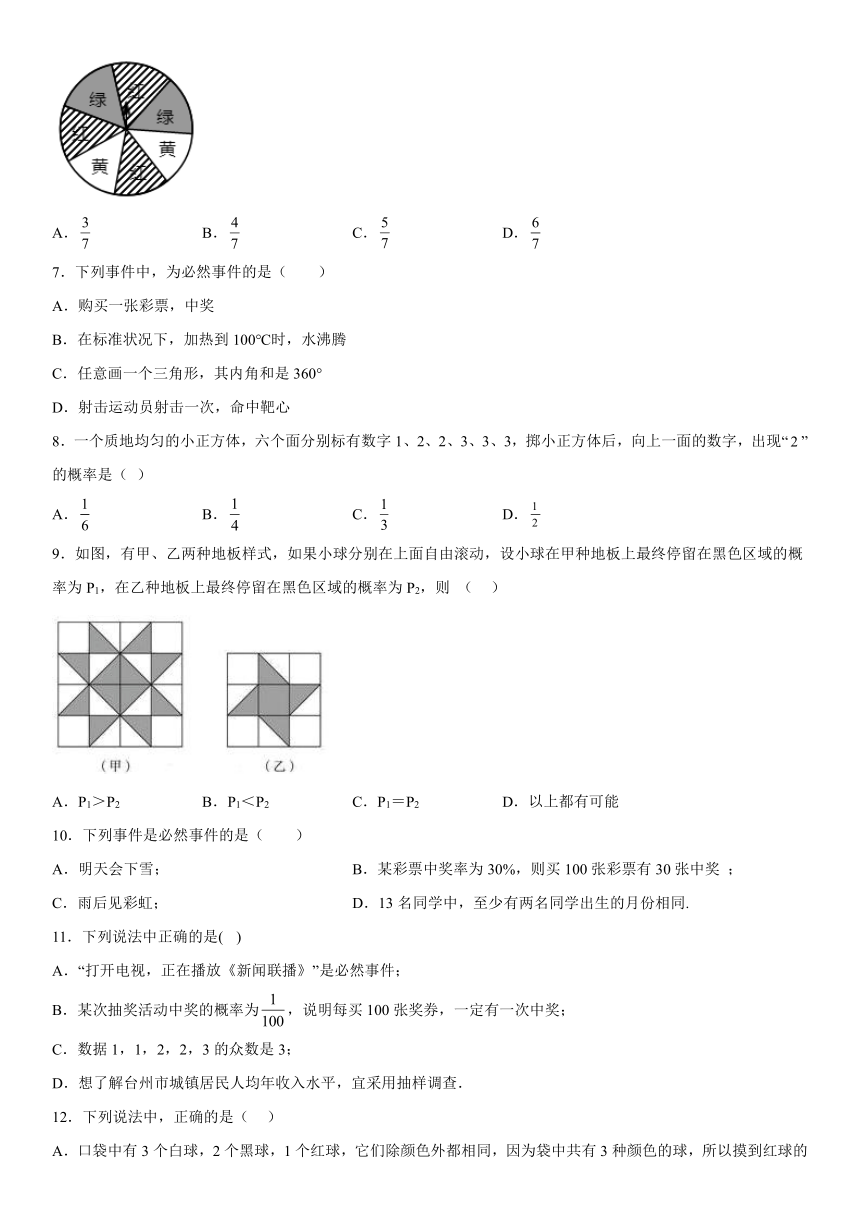
6.如图,是一个质地均匀的转盘,转盘分成7个大小相同的扇形,颜色分为红、绿、黄三种颜色.指针的位置固定,转动转盘后任其自由停止;其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).则指针指向绿色或黄色的概率为( )
A. B. C. D.
7.下列事件中,为必然事件的是( )
A.购买一张彩票,中奖
B.在标准状况下,加热到100℃时,水沸腾
C.任意画一个三角形,其内角和是360°
D.射击运动员射击一次,命中靶心
8.一个质地均匀的小正方体,六个面分别标有数字1、2、2、3、3、3,掷小正方体后,向上一面的数字,出现“”的概率是( )
A. B. C. D.
9.如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则 ( )
A.P1>P2 B.P1<P2 C.P1=P2 D.以上都有可能
10.下列事件是必然事件的是( )
A.明天会下雪; B.某彩票中奖率为30%,则买100张彩票有30张中奖 ;
C.雨后见彩虹; D.13名同学中,至少有两名同学出生的月份相同.
11.下列说法中正确的是( )
A.“打开电视,正在播放《新闻联播》”是必然事件;
B.某次抽奖活动中奖的概率为,说明每买100张奖券,一定有一次中奖;
C.数据1,1,2,2,3的众数是3;
D.想了解台州市城镇居民人均年收入水平,宜采用抽样调查.
12.下列说法中,正确的是( )
A.口袋中有3个白球,2个黑球,1个红球,它们除颜色外都相同,因为袋中共有3种颜色的球,所以摸到红球的概率是
B.掷一枚硬币两次,可能的结果为两次都是正面,一次正面一次反面,两次都是反面,所以掷出两次都是反面的概率为
C.小明参加篮球投篮游戏,因为投篮一次,只有两种可能的结果,不是“投中”就是“未投中”,所以投中的概率为
D.掷一枚只有六个面骰子,合数点朝上的概率是
二、填空题(本大题共8小题,每小题3分,共24分)
13.一箱饮品(每箱12瓶)中有2瓶的盖内印有“奖”字,小明的爸爸买了一箱这种品牌的饮品,但连续打开2瓶均未中奖,此时小明在剩下的饮品中任意拿一瓶,那么他拿出的这瓶饮品中奖的机会是 _____.
14.一般地,如果一个试验有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为:________.必然事件发生的概率为__,不可能事件发生的概率为___,随机事件A发生的概率是_______.
15.一个不透明的口袋中有3个红球,2个白球和1个黑球,它们除颜色外完全相同,从中任意摸出一个球,则摸出的是黑球的概率是____.
16.一个不透明的袋子中装有5个小球,其中3个红球、2个黑球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率是______.
17.一个不透明的袋子里装有红、白、蓝三种颜色的球分别有3个、5个、8个.它们除颜色外其余都相同,从中随机的摸出一个,摸到白球的概率是______.
18.九年级某班有50名同学,在一次数学测试中有35名同学达到优秀,课上老师随机抽取一名同学回答问题,则抽到在此次测试中数学成绩达到优秀的概率是_____.
19.小明的卷子夹里放了大小相同的试卷共页,其中语文页、数学页、英语页,他随机地从卷子夹中抽出页,抽出的试卷恰好是数学试卷的概率为____.
20.一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其它完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在20%附近,口袋中白球最有可能有__________个;
三、解答题(本大题共5小题,每小题8分,共40分)
21.某沿海城市将进行旧城改造,该市地区面积约占40%,其余为郊区, 计划将城区面积的40%建成“公寓式”住宅,面积占城区30% 的工厂迁至北部郊区的荒废地带,其余均为商业区,而郊区的北部已有工厂占郊区面积的20%,南部沿海一带将被开发为别墅区占20%,原占地40%农田不变.当电脑把该市新城郊规划图显示在屏幕上时,任意点击一下鼠标,则被点击点是下列位置的概率是多少
(1)别墅区, (2)居住区, (3)商业区 ,(4)工业区
22.在一个口袋中只装有4个白球和6个红球,它们除颜色外完全相同.
(1)事件“从口袋中随机摸出一个球是绿球”发生的概率是___;
(2)事件“从口袋中随机摸出一个球是红球”发生的概率是___;
(3)现从口袋中取走若干个红球,并放入相同数量的白球,充分摇匀后,要使从口袋中随机摸出一个球是白球的概率是,求取走了多少个红球?
23.为了调查某校初三学生周末手机使用情况,小陆从该校所有学生中随机调查了40名学生,发现其中有10名学生周末使用手机时间超过3小时.
(1)如果你在该校随机调查一个初三学生,估计该学生周末使用手机超过3小时的概率是多少?
(2)已知该校初三共有720名学生,请你估计该校周末使用手机时间超过3小时的学生共有多少人?
24.某校开展对学生“劳动习惯”情况的调查,为了解全校500名学生“主动做家务事”的情况,随机抽查了该校部分学生一周“主动做家务事”的次数,制成了如下的统计表和统计图.
次数 0 1 2 3 4
人数 3 6 13 12
(1)根据以上信息,求在被抽查学生中,一周“主动做家务事”3次的人数;
(2)若在被抽查学生中随机抽取1名,则抽到的学生一周“主动做家务事”不多于2次的概率是多少?
(3)根据样本数据,估计全校学生一周“主动做家务事”3次的人数.
25.某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如图的统计图.请根据相关信息,解答下列问题:
(1)扇形统计图中的______,条形统计图中的______;
(2)从该样本中随机抽取一名学生的睡眠时长,恰好是7h的概率是______;
(3)若该校共有1600名学生,则根据样本数据,估计该校初中学生每天睡眠时间少于8小时的人数.
参考答案:
1.D
2.C
3.C
4.B
5.C
6.B
7.B
8.C
9.A
10.D
11.D
12.D
13.
14. P(A)= 1 0 0与1之间的一个常数
15.
16.
17./0.3125
18..
19.
20.8
21.(1)0.12,(2)0.28,(3)0.24,(4)0.24
22.(1)0
(2)
(3)4个
23.(1)
(2)180人
24.(1)16人;(2)0.44;(3)160人
25.(1)25,15;
(2);
(3)1080人.
一、单选题(本大题共12小题,每小题3分,共36分)
1.如图,一个圆形转盘被平均分成6个全等的扇形,任意旋转这个转盘1次,则当转盘停止转动时,指针指向阴影部分的概率是( )
A. B. C. D.
2.下列事件中是必然事件的为:( )
A.连续抛一枚均匀硬币2次,有1次正面朝上
B.二次函数图象与x轴总有交点
C.所有的等腰直角三角形都是相似的
D.通过旋转变换得到的图形,也可以通过平移变换得到
3.如图,一副普通扑克牌中的13张黑桃牌(J代表11,Q代表12,K代表13),将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数是2的倍数的概率为( )
A. B. C. D.
4.盒子里有10个球,它们只有颜色不同,其中红球有7个,黄球有2个,黑球有1个.幸幸从中任意摸一个球,下面说法正确的是( )
A.一定是红球 B.摸出红球的可能性最大
C.不可能是黑球 D.摸出黄球的可能性最小
5.对于事件“某学习小组14人中至少有2人在同一个月过生日”,从发生的可能性大小判断,你认为该事件属于( )
A.不可能事件 B.随机事件 C.必然事件 D.无法判断
6.如图,是一个质地均匀的转盘,转盘分成7个大小相同的扇形,颜色分为红、绿、黄三种颜色.指针的位置固定,转动转盘后任其自由停止;其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).则指针指向绿色或黄色的概率为( )
A. B. C. D.
7.下列事件中,为必然事件的是( )
A.购买一张彩票,中奖
B.在标准状况下,加热到100℃时,水沸腾
C.任意画一个三角形,其内角和是360°
D.射击运动员射击一次,命中靶心
8.一个质地均匀的小正方体,六个面分别标有数字1、2、2、3、3、3,掷小正方体后,向上一面的数字,出现“”的概率是( )
A. B. C. D.
9.如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则 ( )
A.P1>P2 B.P1<P2 C.P1=P2 D.以上都有可能
10.下列事件是必然事件的是( )
A.明天会下雪; B.某彩票中奖率为30%,则买100张彩票有30张中奖 ;
C.雨后见彩虹; D.13名同学中,至少有两名同学出生的月份相同.
11.下列说法中正确的是( )
A.“打开电视,正在播放《新闻联播》”是必然事件;
B.某次抽奖活动中奖的概率为,说明每买100张奖券,一定有一次中奖;
C.数据1,1,2,2,3的众数是3;
D.想了解台州市城镇居民人均年收入水平,宜采用抽样调查.
12.下列说法中,正确的是( )
A.口袋中有3个白球,2个黑球,1个红球,它们除颜色外都相同,因为袋中共有3种颜色的球,所以摸到红球的概率是
B.掷一枚硬币两次,可能的结果为两次都是正面,一次正面一次反面,两次都是反面,所以掷出两次都是反面的概率为
C.小明参加篮球投篮游戏,因为投篮一次,只有两种可能的结果,不是“投中”就是“未投中”,所以投中的概率为
D.掷一枚只有六个面骰子,合数点朝上的概率是
二、填空题(本大题共8小题,每小题3分,共24分)
13.一箱饮品(每箱12瓶)中有2瓶的盖内印有“奖”字,小明的爸爸买了一箱这种品牌的饮品,但连续打开2瓶均未中奖,此时小明在剩下的饮品中任意拿一瓶,那么他拿出的这瓶饮品中奖的机会是 _____.
14.一般地,如果一个试验有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为:________.必然事件发生的概率为__,不可能事件发生的概率为___,随机事件A发生的概率是_______.
15.一个不透明的口袋中有3个红球,2个白球和1个黑球,它们除颜色外完全相同,从中任意摸出一个球,则摸出的是黑球的概率是____.
16.一个不透明的袋子中装有5个小球,其中3个红球、2个黑球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率是______.
17.一个不透明的袋子里装有红、白、蓝三种颜色的球分别有3个、5个、8个.它们除颜色外其余都相同,从中随机的摸出一个,摸到白球的概率是______.
18.九年级某班有50名同学,在一次数学测试中有35名同学达到优秀,课上老师随机抽取一名同学回答问题,则抽到在此次测试中数学成绩达到优秀的概率是_____.
19.小明的卷子夹里放了大小相同的试卷共页,其中语文页、数学页、英语页,他随机地从卷子夹中抽出页,抽出的试卷恰好是数学试卷的概率为____.
20.一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其它完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在20%附近,口袋中白球最有可能有__________个;
三、解答题(本大题共5小题,每小题8分,共40分)
21.某沿海城市将进行旧城改造,该市地区面积约占40%,其余为郊区, 计划将城区面积的40%建成“公寓式”住宅,面积占城区30% 的工厂迁至北部郊区的荒废地带,其余均为商业区,而郊区的北部已有工厂占郊区面积的20%,南部沿海一带将被开发为别墅区占20%,原占地40%农田不变.当电脑把该市新城郊规划图显示在屏幕上时,任意点击一下鼠标,则被点击点是下列位置的概率是多少
(1)别墅区, (2)居住区, (3)商业区 ,(4)工业区
22.在一个口袋中只装有4个白球和6个红球,它们除颜色外完全相同.
(1)事件“从口袋中随机摸出一个球是绿球”发生的概率是___;
(2)事件“从口袋中随机摸出一个球是红球”发生的概率是___;
(3)现从口袋中取走若干个红球,并放入相同数量的白球,充分摇匀后,要使从口袋中随机摸出一个球是白球的概率是,求取走了多少个红球?
23.为了调查某校初三学生周末手机使用情况,小陆从该校所有学生中随机调查了40名学生,发现其中有10名学生周末使用手机时间超过3小时.
(1)如果你在该校随机调查一个初三学生,估计该学生周末使用手机超过3小时的概率是多少?
(2)已知该校初三共有720名学生,请你估计该校周末使用手机时间超过3小时的学生共有多少人?
24.某校开展对学生“劳动习惯”情况的调查,为了解全校500名学生“主动做家务事”的情况,随机抽查了该校部分学生一周“主动做家务事”的次数,制成了如下的统计表和统计图.
次数 0 1 2 3 4
人数 3 6 13 12
(1)根据以上信息,求在被抽查学生中,一周“主动做家务事”3次的人数;
(2)若在被抽查学生中随机抽取1名,则抽到的学生一周“主动做家务事”不多于2次的概率是多少?
(3)根据样本数据,估计全校学生一周“主动做家务事”3次的人数.
25.某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如图的统计图.请根据相关信息,解答下列问题:
(1)扇形统计图中的______,条形统计图中的______;
(2)从该样本中随机抽取一名学生的睡眠时长,恰好是7h的概率是______;
(3)若该校共有1600名学生,则根据样本数据,估计该校初中学生每天睡眠时间少于8小时的人数.
参考答案:
1.D
2.C
3.C
4.B
5.C
6.B
7.B
8.C
9.A
10.D
11.D
12.D
13.
14. P(A)= 1 0 0与1之间的一个常数
15.
16.
17./0.3125
18..
19.
20.8
21.(1)0.12,(2)0.28,(3)0.24,(4)0.24
22.(1)0
(2)
(3)4个
23.(1)
(2)180人
24.(1)16人;(2)0.44;(3)160人
25.(1)25,15;
(2);
(3)1080人.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
