湘教版数学九年级上册 3.4.1 相似三角形的判定 课件(共28张PPT)
文档属性
| 名称 | 湘教版数学九年级上册 3.4.1 相似三角形的判定 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 481.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 06:47:26 | ||
图片预览




文档简介
(共28张PPT)
3.4 相似三角形的判定与性质
第3章 图形的相似
3.4.1 相似三角形的判定
教学目标
了解相似三角形的判定方法会用平行法判定两个三角形相似
重点: 用平行法判定两个三角形相似
难点:平行法判定三角形相似定理的推导
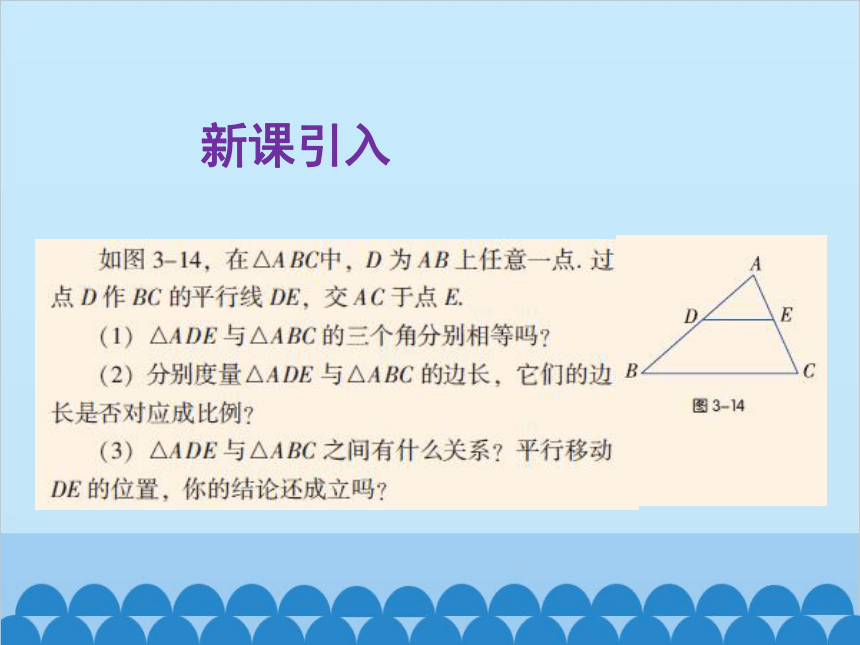
新课引入
由此得出结论:
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
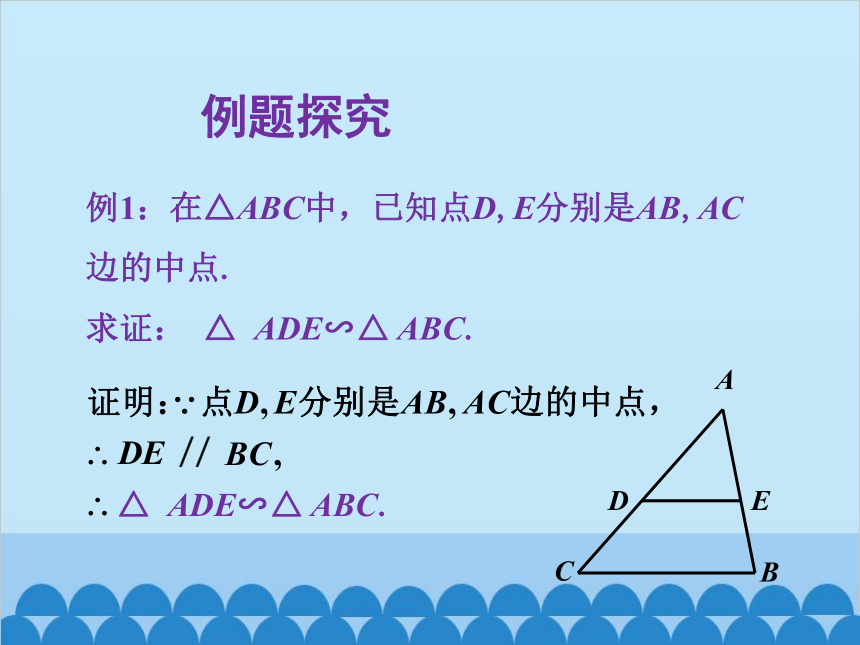
例题探究
例1:在△ABC中,已知点D,E分别是AB,AC
边的中点.
求证: △ ADE∽△ ABC.
△ ADE∽△ ABC.
A
B
C
D
E
例2:点D为△ABC的边AB的中点,过点D作
DE BC交AB于点E.延长DE至点F,使DE=EF.
求证:△BFE∽△ ACB.
△ ADE∽△ ACB.
DE // BC,
DE // BC,
△ BFE∽△ ACB.
A
B
C
D
E
F
A
B
C
A'
C'
B'
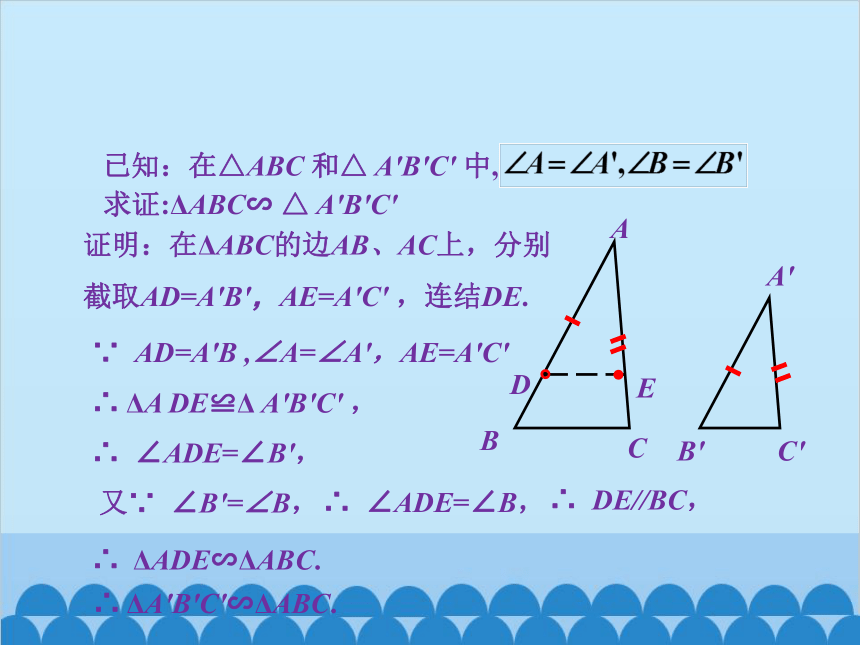
求证:ΔABC∽ △ A'B'C'
已知:在△ABC 和△ A'B'C' 中,
D
E
证明:在ΔABC的边AB、AC上,分别
截取AD=A'B',AE=A'C' ,连结DE.
∵ AD=A'B ,∠A=∠A',AE=A'C'
∴ ΔA DE≌Δ A'B'C' ,
∴ ∠ADE=∠B',
又∵ ∠B'=∠B,
∴ ∠ADE=∠B,
∴ DE//BC,
∴ ΔADE∽ΔABC.
∴ ΔA'B'C'∽ΔABC.
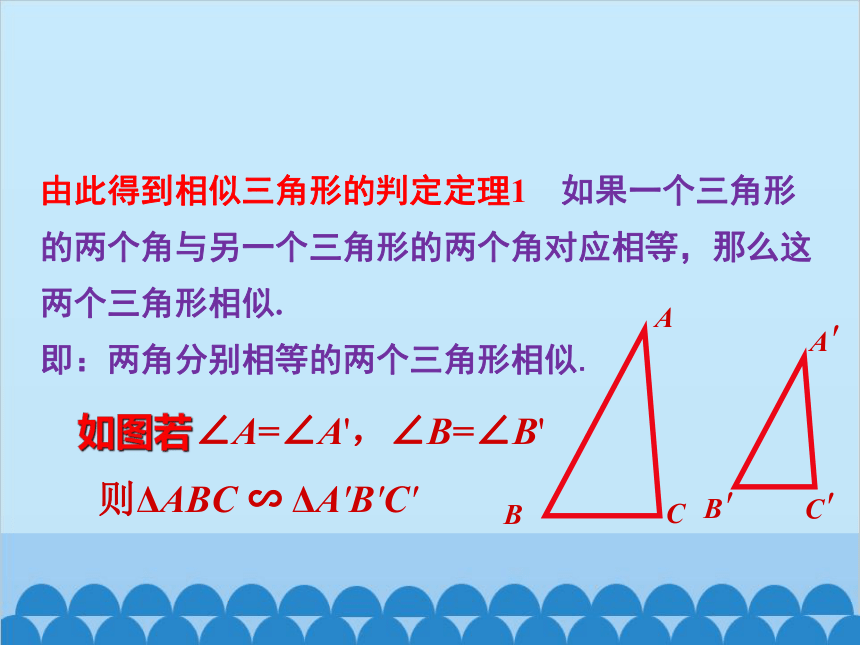
由此得到相似三角形的判定定理1 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
即:两角分别相等的两个三角形相似.
C
A
A'
B
B'
C'
∠A=∠A',∠B=∠B'
则ΔABC ∽ ΔA'B'C'
如图若
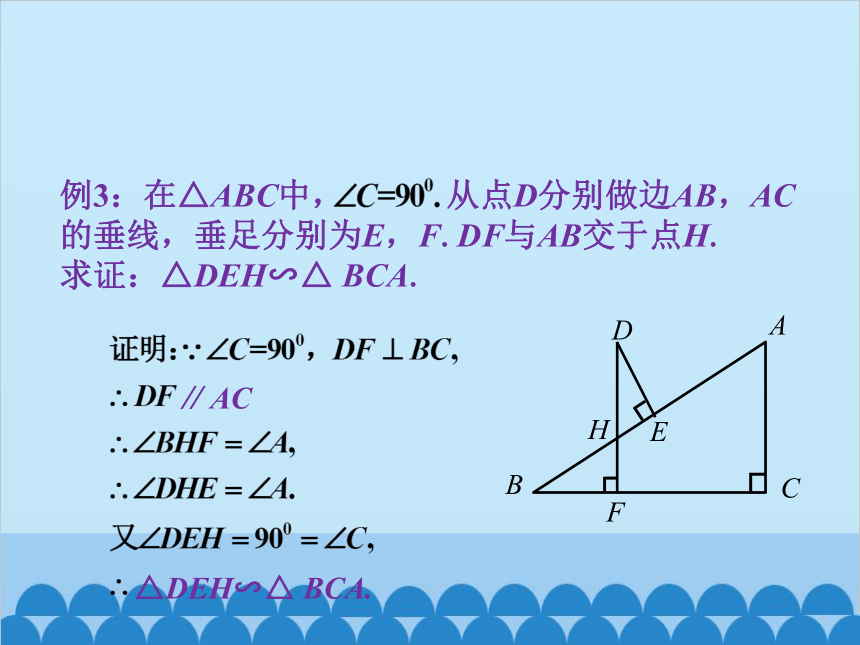
例3:在△ABC中, 从点D分别做边AB,AC的垂线,垂足分别为E,F.DF与AB交于点H. 求证:△DEH∽△ BCA.
△DEH∽△ BCA.
// AC
B
A
C
H
F
E
D
例4:在Rt△ABC与Rt△DEF中, 若 求EF的长.
△DEF∽△ ABC
A
C
B
D
F
E
已知:在△ABC 和△ A'B'C' 中∠A=∠A' ,
求证:ΔABC∽ △ A'B'C'
证明:在△ABC的边AB(或延长线)上
截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∴ △ADE∽△ABC,
∵
A'
B'
C'
A
B
C
E
D
∴△ADE ≌ △
∴ △ ∽△ABC
由此得到相似三角形的判定定理2 如果一个三角形的两条边与另一个三角形的两条边对应成比例,且夹角相等,那么这两个三角形相似.
即:两边对应成比例且夹角相等的两个三角形相似.
∠A=∠A',
则 ΔABC ∽ ΔA'B'C'
A'B' A'C'
=
如图若
AB AC
A'B'C'
A'B'C'
∵∠A=∠A',
C
A
A'
B
B'
C'
例5 在△ABC与△DEF中,已知
AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm.
求证:△ABC∽△ DEF.
A
B
C
D
E
F
例6:在△ABC中,CD是边AB上的高,
且
A
B
D
C
已知:在△ABC 和△ A'B'C' 中,
求证:ΔABC∽ △ A'B'C'
A'
B'
C'
A
B
C
E
D
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∴△ADE∽△ABC,
∵
∴
因此
又
∴△ADE≌ △
A'B'C'
∴ △ ∽△ ABC
A'B'C'
由此得到相似三角形的判定定理3 如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
即:三边成比例的两个三角形相似.
AB AC
A'B' A'C'
=
如图若
=
BC
B'C'
C
A
A'
B
B'
C'
则 ΔABC ∽ ΔA'B'C'
例 7 在△ ABC 和△ A'B'C'中,AB=6cm,BC=8cm,AC=10cm,A'B'=18cm,B'C'=24cm,A'C'=30cm,试证明△ ABC 和△A’B’C相似
解:∵
1
AB
6
=
A'B'
18
=
3
1
BC
8
=
B'C'
24
=
3
AB AC
A'B' A'C'
=
∴
=
BC
B'C'
1
AC
10
=
A'C'
30
=
3
∴ΔABC ∽ ΔA'B'C'
课堂练习
1.如图,已知点O在四边形ABCD的对角线AC上,OE∥ BC,OF∥CD.试判断四边形AEOF与四边形ABCD是否相似,并说明理由.
解:∵OE∥BC,OF∥CD,
∴∠AEO=∠ABC,∠AOE=∠ACB,
∠AOF=∠ACD,∠AFO=∠ADC.
∴∠AOE+∠AOF=∠ACB+∠ACD,即∠EOF=∠BCD.
又∵OE∥BC,OF∥CD,
∴△AOE~△ACB,△AOF~ACD.
∴四边形AEOF与四边形ABCD相似.
2.已知:在△ABC与△DEF中,∠A=48°,
∠B=82°,∠D=48°,∠F=50°.
求证:△ABC∽△DEF.
解:
在△DEF中,
∠E = 180°-∠D -∠F
= 180°-48°-50°
= 82°.
∵ ∠A = ∠D = 48°,∠B =∠E =82°,
∴ △ABC∽△DEF. (两角对应相等的两个三
角形相似)
3.已知在Rt△ABC与Rt△ 中,∠A =∠A′= 90°,AB=6cm,AC=4.8cm, =5cm, =3cm.
求证:△ ∽△ABC.
证明:
∴△ABC∽△ .
4.如图,O为△ABC内一点,D、E、F
分别是OA、OB、OC中点. 求证:△ABC∽△DEF.
A
B
C
O
D
F
E
证明:
△ABC ∽△DEF.
如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是
否相似,并说明理由;
(3)画一个三角形,使它的
三个顶点为P1,P2,P3,P4,
P5中的3个格点并且与△ABC相似.
(要求:用尺规作图,保留痕迹,不写作法与证明)
能力提升
(3)△P4P5P2,作图略.
课堂小结
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似;
两边对应成比例且夹角相等,两三角形相似(SAS)
相似三角形的判定方法
三边对应成比例,两三角形相似.(SSS)
两角分别相等的两个三角形相似(AA)
一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似。(HL)
通过本小节,你有什么收获?
你还存在哪些疑问,和同伴交流。
3.4 相似三角形的判定与性质
第3章 图形的相似
3.4.1 相似三角形的判定
教学目标
了解相似三角形的判定方法会用平行法判定两个三角形相似
重点: 用平行法判定两个三角形相似
难点:平行法判定三角形相似定理的推导
新课引入
由此得出结论:
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
例题探究
例1:在△ABC中,已知点D,E分别是AB,AC
边的中点.
求证: △ ADE∽△ ABC.
△ ADE∽△ ABC.
A
B
C
D
E
例2:点D为△ABC的边AB的中点,过点D作
DE BC交AB于点E.延长DE至点F,使DE=EF.
求证:△BFE∽△ ACB.
△ ADE∽△ ACB.
DE // BC,
DE // BC,
△ BFE∽△ ACB.
A
B
C
D
E
F
A
B
C
A'
C'
B'
求证:ΔABC∽ △ A'B'C'
已知:在△ABC 和△ A'B'C' 中,
D
E
证明:在ΔABC的边AB、AC上,分别
截取AD=A'B',AE=A'C' ,连结DE.
∵ AD=A'B ,∠A=∠A',AE=A'C'
∴ ΔA DE≌Δ A'B'C' ,
∴ ∠ADE=∠B',
又∵ ∠B'=∠B,
∴ ∠ADE=∠B,
∴ DE//BC,
∴ ΔADE∽ΔABC.
∴ ΔA'B'C'∽ΔABC.
由此得到相似三角形的判定定理1 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
即:两角分别相等的两个三角形相似.
C
A
A'
B
B'
C'
∠A=∠A',∠B=∠B'
则ΔABC ∽ ΔA'B'C'
如图若
例3:在△ABC中, 从点D分别做边AB,AC的垂线,垂足分别为E,F.DF与AB交于点H. 求证:△DEH∽△ BCA.
△DEH∽△ BCA.
// AC
B
A
C
H
F
E
D
例4:在Rt△ABC与Rt△DEF中, 若 求EF的长.
△DEF∽△ ABC
A
C
B
D
F
E
已知:在△ABC 和△ A'B'C' 中∠A=∠A' ,
求证:ΔABC∽ △ A'B'C'
证明:在△ABC的边AB(或延长线)上
截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∴ △ADE∽△ABC,
∵
A'
B'
C'
A
B
C
E
D
∴△ADE ≌ △
∴ △ ∽△ABC
由此得到相似三角形的判定定理2 如果一个三角形的两条边与另一个三角形的两条边对应成比例,且夹角相等,那么这两个三角形相似.
即:两边对应成比例且夹角相等的两个三角形相似.
∠A=∠A',
则 ΔABC ∽ ΔA'B'C'
A'B' A'C'
=
如图若
AB AC
A'B'C'
A'B'C'
∵∠A=∠A',
C
A
A'
B
B'
C'
例5 在△ABC与△DEF中,已知
AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm.
求证:△ABC∽△ DEF.
A
B
C
D
E
F
例6:在△ABC中,CD是边AB上的高,
且
A
B
D
C
已知:在△ABC 和△ A'B'C' 中,
求证:ΔABC∽ △ A'B'C'
A'
B'
C'
A
B
C
E
D
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∴△ADE∽△ABC,
∵
∴
因此
又
∴△ADE≌ △
A'B'C'
∴ △ ∽△ ABC
A'B'C'
由此得到相似三角形的判定定理3 如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
即:三边成比例的两个三角形相似.
AB AC
A'B' A'C'
=
如图若
=
BC
B'C'
C
A
A'
B
B'
C'
则 ΔABC ∽ ΔA'B'C'
例 7 在△ ABC 和△ A'B'C'中,AB=6cm,BC=8cm,AC=10cm,A'B'=18cm,B'C'=24cm,A'C'=30cm,试证明△ ABC 和△A’B’C相似
解:∵
1
AB
6
=
A'B'
18
=
3
1
BC
8
=
B'C'
24
=
3
AB AC
A'B' A'C'
=
∴
=
BC
B'C'
1
AC
10
=
A'C'
30
=
3
∴ΔABC ∽ ΔA'B'C'
课堂练习
1.如图,已知点O在四边形ABCD的对角线AC上,OE∥ BC,OF∥CD.试判断四边形AEOF与四边形ABCD是否相似,并说明理由.
解:∵OE∥BC,OF∥CD,
∴∠AEO=∠ABC,∠AOE=∠ACB,
∠AOF=∠ACD,∠AFO=∠ADC.
∴∠AOE+∠AOF=∠ACB+∠ACD,即∠EOF=∠BCD.
又∵OE∥BC,OF∥CD,
∴△AOE~△ACB,△AOF~ACD.
∴四边形AEOF与四边形ABCD相似.
2.已知:在△ABC与△DEF中,∠A=48°,
∠B=82°,∠D=48°,∠F=50°.
求证:△ABC∽△DEF.
解:
在△DEF中,
∠E = 180°-∠D -∠F
= 180°-48°-50°
= 82°.
∵ ∠A = ∠D = 48°,∠B =∠E =82°,
∴ △ABC∽△DEF. (两角对应相等的两个三
角形相似)
3.已知在Rt△ABC与Rt△ 中,∠A =∠A′= 90°,AB=6cm,AC=4.8cm, =5cm, =3cm.
求证:△ ∽△ABC.
证明:
∴△ABC∽△ .
4.如图,O为△ABC内一点,D、E、F
分别是OA、OB、OC中点. 求证:△ABC∽△DEF.
A
B
C
O
D
F
E
证明:
△ABC ∽△DEF.
如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是
否相似,并说明理由;
(3)画一个三角形,使它的
三个顶点为P1,P2,P3,P4,
P5中的3个格点并且与△ABC相似.
(要求:用尺规作图,保留痕迹,不写作法与证明)
能力提升
(3)△P4P5P2,作图略.
课堂小结
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似;
两边对应成比例且夹角相等,两三角形相似(SAS)
相似三角形的判定方法
三边对应成比例,两三角形相似.(SSS)
两角分别相等的两个三角形相似(AA)
一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似。(HL)
通过本小节,你有什么收获?
你还存在哪些疑问,和同伴交流。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
