人教版七年级下册 5.1.3 同位角、内错角、同旁内角 课件(共24张PPT)
文档属性
| 名称 | 人教版七年级下册 5.1.3 同位角、内错角、同旁内角 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 07:10:14 | ||
图片预览


文档简介
(共24张PPT)
5.1.2 同位角、内错角、同旁内角
人教版七年级《数学》下册
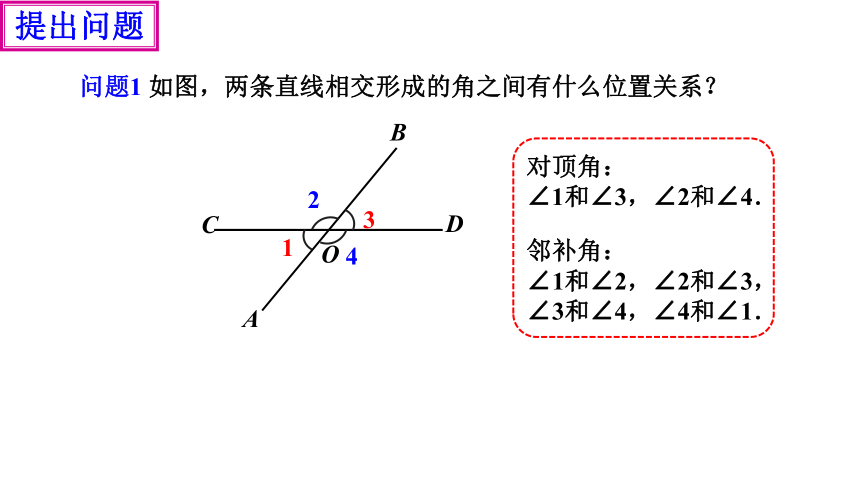
问题1 如图,两条直线相交形成的角之间有什么位置关系?
O
B
A
D
C
1
2
3
4
对顶角:
∠1和∠3,∠2和∠4.
邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.
提出问题
(1)三条直线交点的个数有一个,即三条直线交于一点;
(2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;
(3)三条直线交点的个数有三个,即三条直线两两相交.
可以根据交点的个数进行讨论,也可以根据相截情况进行讨论:
问题2 三条直线相交如何描述它们的位置关系?
提出问题
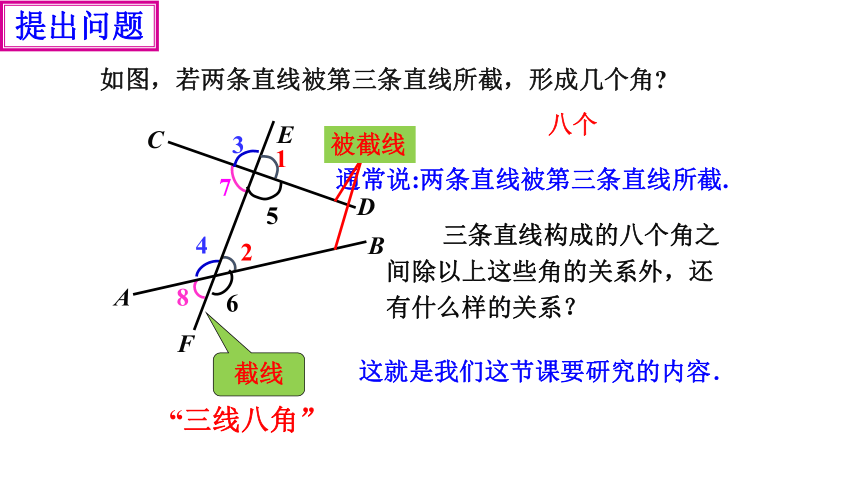
如图,若两条直线被第三条直线所截,形成几个角
1
3
7
5
2
4
8
6
D
C
A
B
E
F
三条直线构成的八个角之间除以上这些角的关系外,还有什么样的关系?
这就是我们这节课要研究的内容.
“三线八角”
八个
通常说:两条直线被第三条直线所截.
截线
被截线
提出问题
F
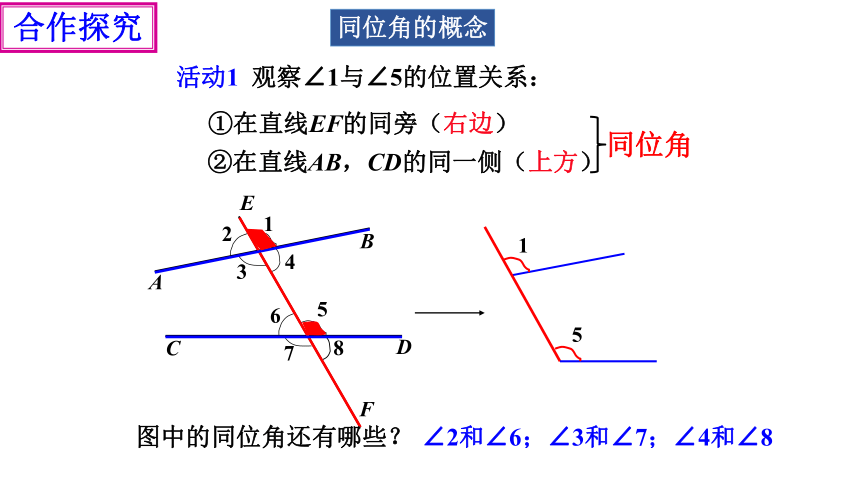
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右边)
②在直线AB,CD的同一侧(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
同位角的概念
合作探究
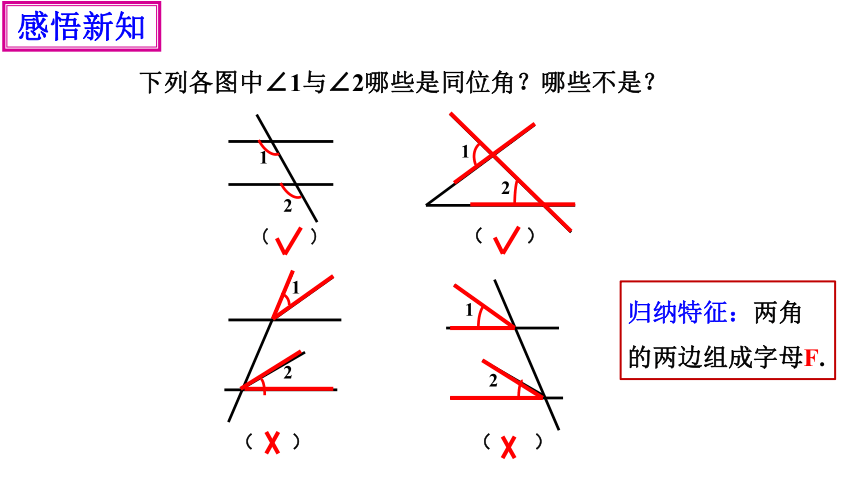
下列各图中∠1与∠2哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
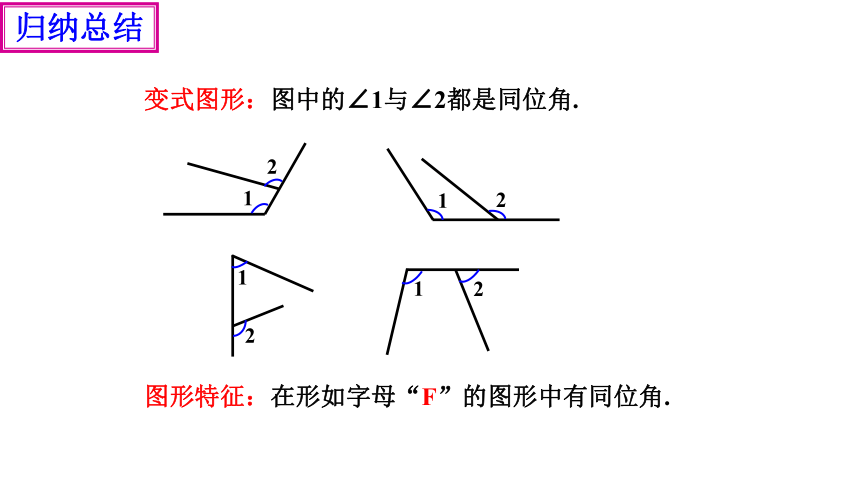
归纳特征:两角的两边组成字母F.
感悟新知
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
归纳总结
A
C
B
D
E
F
1
2
3
4
5
6
7
8
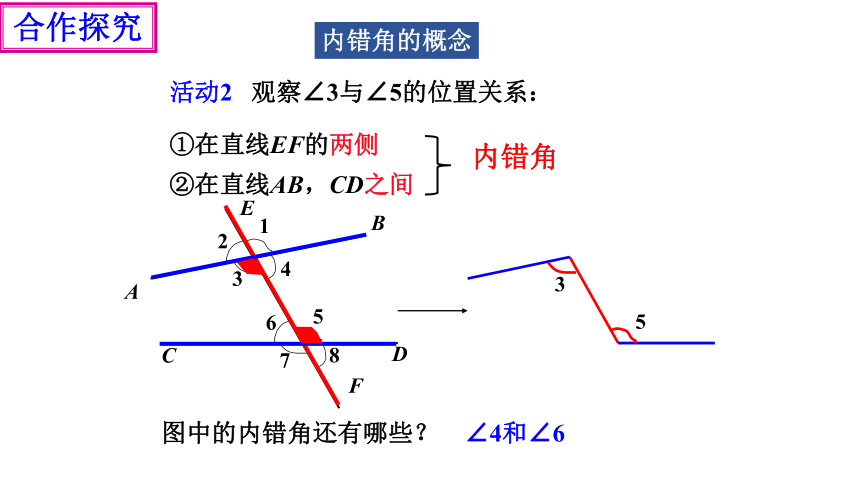
活动2 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB,CD之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
内错角的概念
合作探究
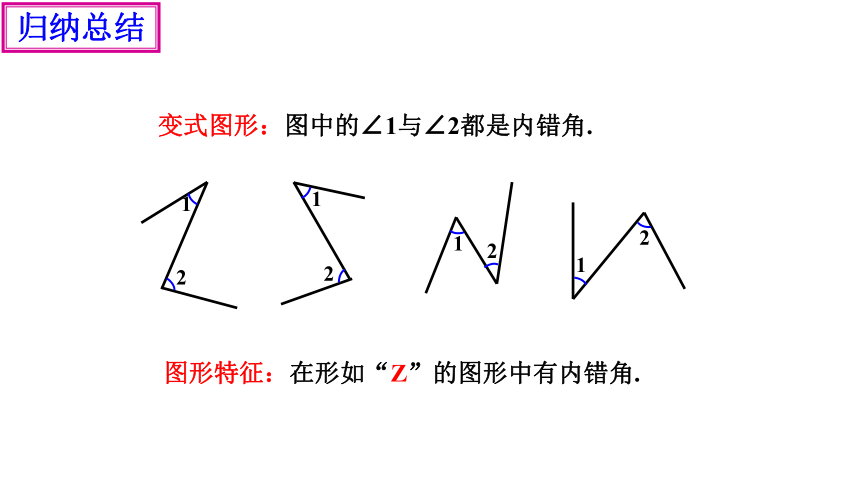
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
归纳总结
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动3 观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB,CD之间
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
同旁内角的概念
合作探究
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
归纳总结
在三线八角中
①同位角有:
②内错角有:
③同旁内角有:
∠1和∠2
∠3和∠4
∠5和∠6
∠7和∠8
∠7和∠2
∠5和∠4
∠7和∠4
∠5和∠2
F
1
3
7
5
2
4
8
6
D
C
A
B
E
归纳总结
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
1.识别哪些角是同位角、内错角、同旁内角.
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
体验新知
5
8
6
3
2.如图,填空:
(1)∠4与∠ 是对顶角;(2)∠4与∠ 是同位角;
(3)∠4与∠ 是内错角;(4)∠4与∠ 是同旁内角;
(5)∠4与∠___、∠___是邻补角.
2
1
a
b
c
6
3
2
1
4
7
8
5
体验新知
3.(1)∠1和∠4是直线_____与直线____被直线______所截
形成的________.
(2)∠2和∠3是直线_____与直线_____被直线_______所截
形成的________.
4
3
2
1
A
B
C
D
内错角
BD
BC
AD
BD
CD
AB
内错角
2
3
1
4
(1)
(2)
体验新知
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
2. 在图形中判断三线八角的方法(描图法):
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,同 位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式(旋转、对称)也是符合的.
小结提升
1.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角
可看成是( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
C
课堂检测
2.如图,∠B 的同旁内角可以是( )
A.∠1 B.∠3
C.∠2 D.∠4
B
课堂检测
3.如图,∠1和∠2不能构成同位角的图形是( )
D
A B C D
课堂检测
4.如图所示,
(1)∠B和∠ECD可看成是直线AB,CE被直
线______所截得的_______角;
(2)∠A和∠ACE可看成是直线______、_____被
直线______所截得的______角.
BD
AB EC
AC
同位
内错
课堂检测
5.如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,
同位角:∠2与∠5,∠4与∠7,
∠1与∠8,∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
体验新知
4
3
2
1
F
E
D
C
B
A
解:∠1和∠2是内错角,
∠1和∠4是同位角.
∠1和∠3是同旁内角,
体验新知
6.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3,∠1和∠4各是什么位置关系的角?
解:如果∠1=∠4,由对顶角相等,
得∠2=∠4,那么 ∠1=∠2.
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?
∵∠3和∠4互补,
即∠4+∠3=180°,
又∵∠1=∠4,
∴∠1+∠3=180°,
即∠1与∠3互补.
6.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3,∠1和∠4各是什么位置关系的角?
体验新知
4
3
2
1
F
E
D
C
B
A
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
5.1.2 同位角、内错角、同旁内角
人教版七年级《数学》下册
问题1 如图,两条直线相交形成的角之间有什么位置关系?
O
B
A
D
C
1
2
3
4
对顶角:
∠1和∠3,∠2和∠4.
邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.
提出问题
(1)三条直线交点的个数有一个,即三条直线交于一点;
(2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;
(3)三条直线交点的个数有三个,即三条直线两两相交.
可以根据交点的个数进行讨论,也可以根据相截情况进行讨论:
问题2 三条直线相交如何描述它们的位置关系?
提出问题
如图,若两条直线被第三条直线所截,形成几个角
1
3
7
5
2
4
8
6
D
C
A
B
E
F
三条直线构成的八个角之间除以上这些角的关系外,还有什么样的关系?
这就是我们这节课要研究的内容.
“三线八角”
八个
通常说:两条直线被第三条直线所截.
截线
被截线
提出问题
F
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右边)
②在直线AB,CD的同一侧(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
同位角的概念
合作探究
下列各图中∠1与∠2哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
归纳特征:两角的两边组成字母F.
感悟新知
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
归纳总结
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动2 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB,CD之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
内错角的概念
合作探究
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
归纳总结
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动3 观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB,CD之间
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
同旁内角的概念
合作探究
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
归纳总结
在三线八角中
①同位角有:
②内错角有:
③同旁内角有:
∠1和∠2
∠3和∠4
∠5和∠6
∠7和∠8
∠7和∠2
∠5和∠4
∠7和∠4
∠5和∠2
F
1
3
7
5
2
4
8
6
D
C
A
B
E
归纳总结
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
1.识别哪些角是同位角、内错角、同旁内角.
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
体验新知
5
8
6
3
2.如图,填空:
(1)∠4与∠ 是对顶角;(2)∠4与∠ 是同位角;
(3)∠4与∠ 是内错角;(4)∠4与∠ 是同旁内角;
(5)∠4与∠___、∠___是邻补角.
2
1
a
b
c
6
3
2
1
4
7
8
5
体验新知
3.(1)∠1和∠4是直线_____与直线____被直线______所截
形成的________.
(2)∠2和∠3是直线_____与直线_____被直线_______所截
形成的________.
4
3
2
1
A
B
C
D
内错角
BD
BC
AD
BD
CD
AB
内错角
2
3
1
4
(1)
(2)
体验新知
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
2. 在图形中判断三线八角的方法(描图法):
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,同 位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式(旋转、对称)也是符合的.
小结提升
1.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角
可看成是( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
C
课堂检测
2.如图,∠B 的同旁内角可以是( )
A.∠1 B.∠3
C.∠2 D.∠4
B
课堂检测
3.如图,∠1和∠2不能构成同位角的图形是( )
D
A B C D
课堂检测
4.如图所示,
(1)∠B和∠ECD可看成是直线AB,CE被直
线______所截得的_______角;
(2)∠A和∠ACE可看成是直线______、_____被
直线______所截得的______角.
BD
AB EC
AC
同位
内错
课堂检测
5.如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,
同位角:∠2与∠5,∠4与∠7,
∠1与∠8,∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
体验新知
4
3
2
1
F
E
D
C
B
A
解:∠1和∠2是内错角,
∠1和∠4是同位角.
∠1和∠3是同旁内角,
体验新知
6.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3,∠1和∠4各是什么位置关系的角?
解:如果∠1=∠4,由对顶角相等,
得∠2=∠4,那么 ∠1=∠2.
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?
∵∠3和∠4互补,
即∠4+∠3=180°,
又∵∠1=∠4,
∴∠1+∠3=180°,
即∠1与∠3互补.
6.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3,∠1和∠4各是什么位置关系的角?
体验新知
4
3
2
1
F
E
D
C
B
A
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
