人教版七年级下册 6.1 平方根 课件(共21张PPT)
文档属性
| 名称 | 人教版七年级下册 6.1 平方根 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 613.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 07:11:34 | ||
图片预览






文档简介
(共21张PPT)
6.1 平方根(1)
人教版七年级《数学》下册
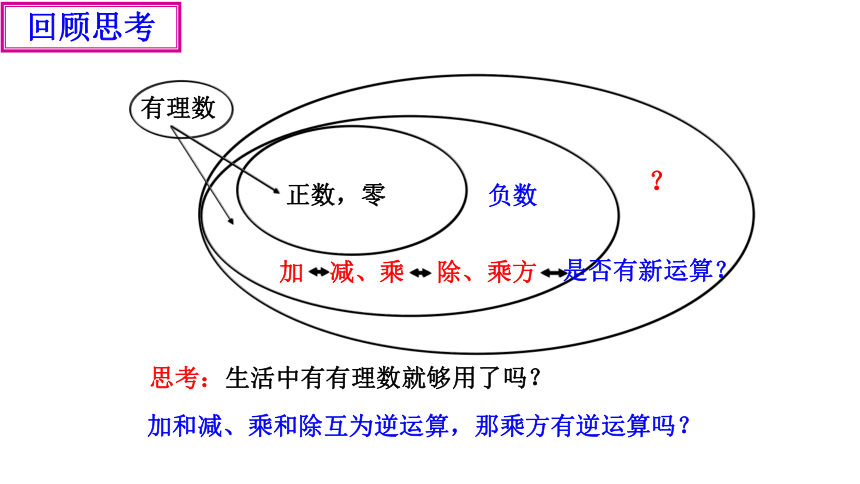
思考:生活中有有理数就够用了吗?
正数,零
负数
加 减、乘 除、乘方
有理数
?
是否有新运算?
加和减、乘和除互为逆运算,那乘方有逆运算吗?
回顾思考
正方形的边长(m) 1 2 0.5
正方形的面积(m2)
1 4 0. 25
12=( )22=( )0.52= ( )
表 一
已知一个正数,求这个正数的平方,这是平方运算.
在我校举行的绘画比赛中,小明同学准备了一些正方形的画布,你能计算出它们的面积吗?
思考:你能从表一发现什么共同点吗?
合作探究
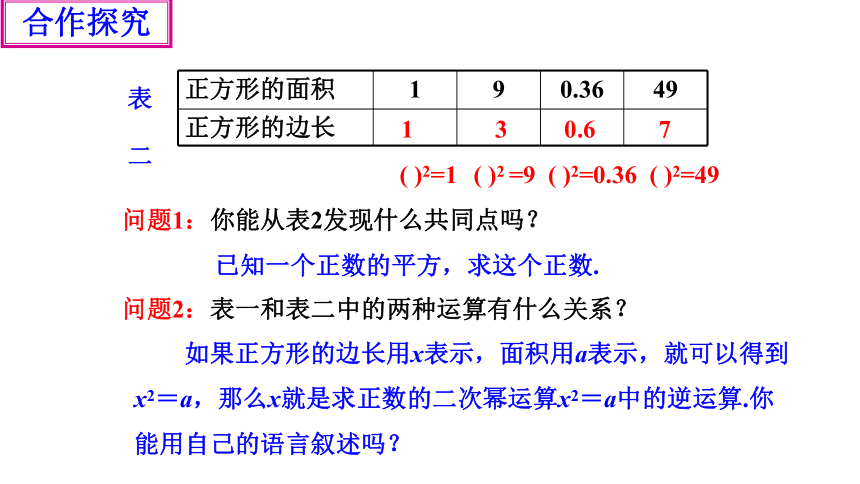
正方形的面积 1 9 0.36 49
正方形的边长
( )2=1 ( )2 =9 ( )2=0.36 ( )2=49
表 二
问题2:表一和表二中的两种运算有什么关系?
1 3 0.6 7
问题1:你能从表2发现什么共同点吗?
已知一个正数的平方,求这个正数.
如果正方形的边长用x表示,面积用a表示,就可以得到x2=a,那么x就是求正数的二次幂运算x2=a中的逆运算.你能用自己的语言叙述吗?
合作探究
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根.
(实际上,正数x就是二次幂运算x2=a中的正底数).
特别地,我们规定0的算术平方根是0.
类比理解 形成概念
1.因为22=4 ,所以4的算术平方根是__;
2.因为0.52=0.25 ,所以0.25的算术平方根是__;
3.因为 = ,所以 的算术平方根是 .
2
0.5
4
9
a的算术平方根
互为
逆运算
根号
被开方数
读作:根号a
(a≥0)
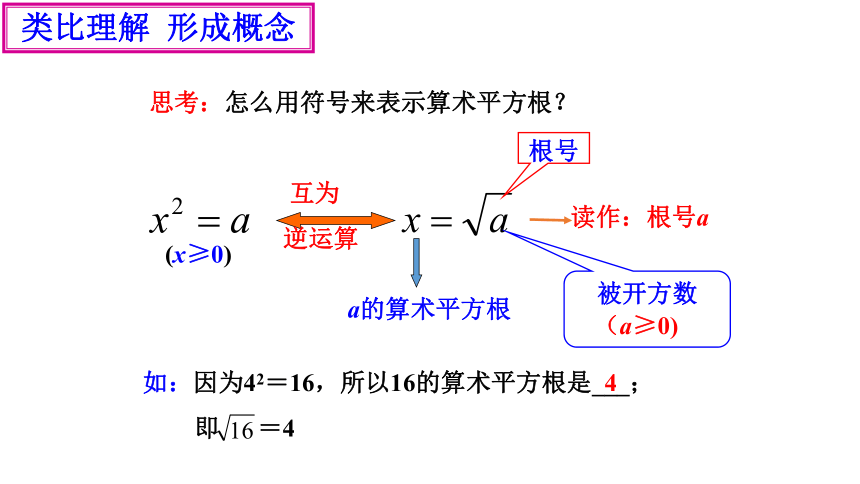
思考:怎么用符号来表示算术平方根?
(x≥0)
如:因为42=16,所以16的算术平方根是___;
即 =4
4
类比理解 形成概念
例1 求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
解:(1)因为102=100,
所以100的算术平方根是10.
即 .
知识运用 体验成功
解:(2)因为 ,
所以 的算术平方根是 .
即 .
例1 求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
知识运用 体验成功
解:(3)因为0.012=0.000 1,
所以0.000 1的算术平方根是0.01.
即 .
例1 求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
知识运用 体验成功
归纳梳理
思考:(1)一个正数的算术平方根有几个?
(2)0的算术平方有几个?
(3)-1有算术平方根吗?负数有算术平方根
一个,是0.
负数没有算术平方根.
一个正数的算术平方根有1个.
发现:被开方数越大,对应算术平方根也 .
越大
例1 求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
算术平方根具有双重非负性
a的算术平方根
非负数
非负数
也就是说,非负数的“算术平方根”是非负数. 负数不存在算术平方根,即当 时, 无意义.
如: 无意义 ; 8是64的算术平方根或
是算术平方根的运算符号.
归纳梳理
2.下列各式有意义吗?为什么.
解:(1) 无意义,负数没有算术平方根;
(2) 有意义,表示5的算术平方根的相反数;
(3) 有意义,表示 (-5)2 的算术平方根.
25
知识应用 强化理解
1.求下列各式的值:
(1) (2) (3)
0.4
4
3
2
(1) =_____.
(3) 的算术平方根等于____.
2
(2)16的算术平方根是____.
(4) 的算术平方根等于______.
√(-3)2
4
3
4
16
16
3.填空
一步运算
两步运算
(5)一个数的算术平方根是3,则这个数是 .
算术平方根是其本身的数是_____.
0和1
9
知识应用 强化理解
4.自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2,有一铁球从19.6 米高的建筑物上自由下落,到达地面需要多长时间 ?
解:将h=19.6代入,得
19.6=4.9t2
化简得,t2=4
∴正数 t=2
即铁球到达地面需要2 秒.
知识应用 强化理解
1.求下列各数的算术平方根:
(1)0.25 (2)121 (3)32
2.下列式子表示什么意义?你能求出它们的值吗?
(1) (2) (3) (4)
1
2
5
课堂检测 体验成功
4.下列运算正确的是( )
A. B.
C. D.
3.下列各式中,无意义的是( )
A. B. C. D.
B
C
课堂检测 体验成功
5.下列命题中,错误的是( )
A. 表示5的算术平方根;
B. 3的算术平方根记作 ;
C. 1是1的算术平方根;
D. 0的算术平方根是它本身
B
课堂检测 体验成功
6.若 ,则x= .
的算术平方根是 .
有意义,则x的取值范围是 .
81
2
x≥2
课堂检测 体验成功
解:设每块地板砖的边长为x m.由题意得
故每块地板砖的边长是0.5 m.
7.用大小完全相同的240 块正方形地板砖,铺一间面积为60 m2的会议室的地面,每块地板砖的边长是多少?
课堂检测 体验成功
概念
逆向思维
特殊到一般
结论
小结·积淀
知识线
思维线
表示
数形结合
对 应
(1)本节课你学习了哪些知识?
(2)在探索知识的过程中,你积累了哪些经验?
主要学习了算术平方根的概念和表示方法,知道了求一个正数的算术平方根与求一个正数的二次幂正好是互逆的过程,因此,求正数的算术平方根实际上可以转化为求一个数的二次幂运算. 只不过,只有正数和0才有算术平方根.
思维方法:求一个正数的算术平方根运算和开平方求一个正数的二次幂运算互为逆运算.
探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决 问题的基本方法和途径.
小结提升
6.1 平方根(1)
人教版七年级《数学》下册
思考:生活中有有理数就够用了吗?
正数,零
负数
加 减、乘 除、乘方
有理数
?
是否有新运算?
加和减、乘和除互为逆运算,那乘方有逆运算吗?
回顾思考
正方形的边长(m) 1 2 0.5
正方形的面积(m2)
1 4 0. 25
12=( )22=( )0.52= ( )
表 一
已知一个正数,求这个正数的平方,这是平方运算.
在我校举行的绘画比赛中,小明同学准备了一些正方形的画布,你能计算出它们的面积吗?
思考:你能从表一发现什么共同点吗?
合作探究
正方形的面积 1 9 0.36 49
正方形的边长
( )2=1 ( )2 =9 ( )2=0.36 ( )2=49
表 二
问题2:表一和表二中的两种运算有什么关系?
1 3 0.6 7
问题1:你能从表2发现什么共同点吗?
已知一个正数的平方,求这个正数.
如果正方形的边长用x表示,面积用a表示,就可以得到x2=a,那么x就是求正数的二次幂运算x2=a中的逆运算.你能用自己的语言叙述吗?
合作探究
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根.
(实际上,正数x就是二次幂运算x2=a中的正底数).
特别地,我们规定0的算术平方根是0.
类比理解 形成概念
1.因为22=4 ,所以4的算术平方根是__;
2.因为0.52=0.25 ,所以0.25的算术平方根是__;
3.因为 = ,所以 的算术平方根是 .
2
0.5
4
9
a的算术平方根
互为
逆运算
根号
被开方数
读作:根号a
(a≥0)
思考:怎么用符号来表示算术平方根?
(x≥0)
如:因为42=16,所以16的算术平方根是___;
即 =4
4
类比理解 形成概念
例1 求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
解:(1)因为102=100,
所以100的算术平方根是10.
即 .
知识运用 体验成功
解:(2)因为 ,
所以 的算术平方根是 .
即 .
例1 求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
知识运用 体验成功
解:(3)因为0.012=0.000 1,
所以0.000 1的算术平方根是0.01.
即 .
例1 求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
知识运用 体验成功
归纳梳理
思考:(1)一个正数的算术平方根有几个?
(2)0的算术平方有几个?
(3)-1有算术平方根吗?负数有算术平方根
一个,是0.
负数没有算术平方根.
一个正数的算术平方根有1个.
发现:被开方数越大,对应算术平方根也 .
越大
例1 求下列各数的算术平方根:
(1)100;(2) ;(3)0.000 1.
算术平方根具有双重非负性
a的算术平方根
非负数
非负数
也就是说,非负数的“算术平方根”是非负数. 负数不存在算术平方根,即当 时, 无意义.
如: 无意义 ; 8是64的算术平方根或
是算术平方根的运算符号.
归纳梳理
2.下列各式有意义吗?为什么.
解:(1) 无意义,负数没有算术平方根;
(2) 有意义,表示5的算术平方根的相反数;
(3) 有意义,表示 (-5)2 的算术平方根.
25
知识应用 强化理解
1.求下列各式的值:
(1) (2) (3)
0.4
4
3
2
(1) =_____.
(3) 的算术平方根等于____.
2
(2)16的算术平方根是____.
(4) 的算术平方根等于______.
√(-3)2
4
3
4
16
16
3.填空
一步运算
两步运算
(5)一个数的算术平方根是3,则这个数是 .
算术平方根是其本身的数是_____.
0和1
9
知识应用 强化理解
4.自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2,有一铁球从19.6 米高的建筑物上自由下落,到达地面需要多长时间 ?
解:将h=19.6代入,得
19.6=4.9t2
化简得,t2=4
∴正数 t=2
即铁球到达地面需要2 秒.
知识应用 强化理解
1.求下列各数的算术平方根:
(1)0.25 (2)121 (3)32
2.下列式子表示什么意义?你能求出它们的值吗?
(1) (2) (3) (4)
1
2
5
课堂检测 体验成功
4.下列运算正确的是( )
A. B.
C. D.
3.下列各式中,无意义的是( )
A. B. C. D.
B
C
课堂检测 体验成功
5.下列命题中,错误的是( )
A. 表示5的算术平方根;
B. 3的算术平方根记作 ;
C. 1是1的算术平方根;
D. 0的算术平方根是它本身
B
课堂检测 体验成功
6.若 ,则x= .
的算术平方根是 .
有意义,则x的取值范围是 .
81
2
x≥2
课堂检测 体验成功
解:设每块地板砖的边长为x m.由题意得
故每块地板砖的边长是0.5 m.
7.用大小完全相同的240 块正方形地板砖,铺一间面积为60 m2的会议室的地面,每块地板砖的边长是多少?
课堂检测 体验成功
概念
逆向思维
特殊到一般
结论
小结·积淀
知识线
思维线
表示
数形结合
对 应
(1)本节课你学习了哪些知识?
(2)在探索知识的过程中,你积累了哪些经验?
主要学习了算术平方根的概念和表示方法,知道了求一个正数的算术平方根与求一个正数的二次幂正好是互逆的过程,因此,求正数的算术平方根实际上可以转化为求一个数的二次幂运算. 只不过,只有正数和0才有算术平方根.
思维方法:求一个正数的算术平方根运算和开平方求一个正数的二次幂运算互为逆运算.
探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决 问题的基本方法和途径.
小结提升
